rGO/CNTs/EP 复合涂层的电荷积聚与消散特性

赵 欣, 邢一龙, 李 梦, 黄成超, 赵皓东, 杨华荣

（中国民用航空飞行学院, 四川 广汉 618307）

飞机机体表面在飞机飞行过程中容易出现静电电荷积聚，对飞行安全及机载电子设备的正常工作存在重大的威胁，因此飞机必须要具备一定的传导并释放机体表面静电电荷的能力。在飞机表面涂覆静电耗散涂层是一种现代飞机常用的应对技术手段，一般要求此类涂层的表面电阻率达到0.5～25 MΩ/sq。目前在该领域中，已有的研究工作多以表征飞机涂层材料的电阻率为主，关于飞机导静电涂层表面电荷的具体变化情况则鲜有涉及。宁亮等[1]研制了一种雷达罩用抗静电涂料,其涂层的表面电阻率随特种碳纤维添加量的增加而降低，当碳纤维添加量达到2.5%（质量分数，下同）时，涂层表面的电阻率低于5 MΩ。杨明坤等[2]利用锡锑氧 化 物（ATO） 与 环 氧 树 脂（EP） 混 合 制 备ATO/EP 涂层，发现ATO 添加量为15.4%的涂层具有107Ω/sq 数量级的表面电阻率，导静电性能较高。在该组份配方的基础上再添加0.3%的石墨烯后，涂层的表面电阻率降为106Ω/sq 数量级，且涂层的防腐蚀性能良好。Mirmohseni 等[3]利用原位聚合方法制备聚苯胺/铜/二氧化钛（PANI/Cu/TiO2）三元纳米复合材料，并将其用于聚氨酯改性涂料，以便获得良好的涂层抗菌和抗静电性能。该研究发现三元纳米复合材料含量为2.0%的聚氨酯涂层的表面电阻率为4×108Ω/sq，达到了抗静电涂层的性能标准。Morsi 等[4]以苯乙烯-丙烯酸丁酯-丙烯酰胺-丙烯酸共聚物（PSBAA）为核，以聚吡咯（PPy）为壳，制备核/壳复合乳液型抗静电涂料。当聚吡咯含量由0%增加到10%，涂层的体积电阻率则相应地从5.48×109Ω•cm 下降到1.2×107Ω•cm，可以满足防静电涂料的应用性能要求[5-7]。

对于介质表面电荷的积聚过程，高压绝缘领域中对绝缘子材料表面电荷变化的相关研究资料丰富，可供借鉴。汪沨等[8]给出了电荷动态分布的表达式，将实测曲线与理论计算曲线进行对比，发现两者具有一致的变化规律。在此基础上，汪沨等[9]在后续研究给出描绘电荷积聚过程的另一个模型，即认为电荷的积聚和消散是同时进行的。当消散时间常数大于积聚时间常数时，电荷的消散速度大于积聚速度，则介质表面电荷无法积聚。王源等[10]研究聚乙烯薄膜表面电荷的变化特性，利用电荷消散的指数函数模型，结合实验数据拟合得到时间常数，并对比不同初始电荷量的消散曲线。结果表明，初始电荷量越高，消散的时间常数越小，消散速度越快。王蓓等[11]研究绝缘子表面电荷的消散过程，通过对实验结果进行指数拟合而得到初始电压、衰减因子等参数，发现衰减因子的拟合结果与电荷单独通过绝缘子内部消散的衰减因子在同一数量级，初始电压也基本相同，即电荷主要通过绝缘子内部消散。田浩等[12]研究影响环氧绝缘材料表面电荷积聚的各种因素，给出积聚电荷量和消散电荷量的表达式，其基本形式与文献[8]给出的相关表达式一致。研究表明，积聚的时间常数小于消散时间常数，是促使经典电荷在表面发生积聚的原因。

已有的研究主要以实验手段表征规律为主，并未从理论模型出发来分析验证其与涂层表面电荷实际变化规律的匹配性。而对于电荷积聚的同时又伴随电荷消散的动态过程（后文简称为复杂过程），则几乎未见公开报道和深入分析。本工作以理论模型为基础，分类探讨电荷积聚、消散以及复杂过程中飞机导静电涂层表面的电荷变化规律。以石墨烯/碳纳米管（rGO/CNTs）为功能填料，环氧树脂（EP）为基体，制备石墨烯/碳纳米管/环氧树脂（rGO/CNTs/EP）复合涂层。通过静电积聚和耗散测试，结合数值拟合分析方法，揭示不同填料参数下复合涂层表面电荷积聚和耗散的变化规律。

1 理论分析及实验方法

1.1 积聚过程的理论分析

绝缘子表面某点电荷密度随时间变化的近似表达式[8]为：

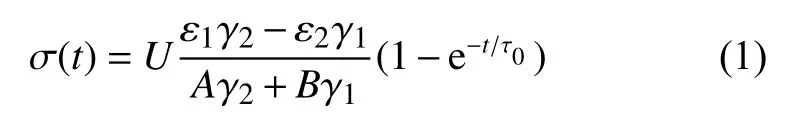
式中：ε1,ε2分别为固体和气体的介电常数；γ1，γ2分别为固体和气体的电导率；A和B为具有长度量纲的系数；τ0为具有时间量纲的电荷积聚时间常数，τ0=(Aε2+Bε1)/(Aγ2+Bγ1)；U为外施直流电压。由于绝缘子材料与本研究制备的rGO/CNTs/EP 涂层同属环氧树脂体系，因此可以采用同样的模型来进行飞机涂层表面电荷积聚过程的研究。

公式（1）的推导过程中，电场强度以气体侧指向固体侧为正，在电压较低的情况下，气体侧未达到放电条件时，γ1＞＞γ2，ε1γ2-ε2γ1＜0，σ(t)为负，表面积累负电荷；当气体侧开始放电时，气体被电离，这时有γ1＜＜γ2，ε1γ2-ε2γ1＞0，σ(t)为正，表面积累正电荷。由电荷积聚的体传导方式[13]可以解释为：当外界场强不足以将气体电离时，表面积累的负电荷是由介质内部负离子或带电杂质粒子受电场作用溢出形成的。而气体电离后，大量正离子由气体侧移动到介质表面。

本研究采用负极性的直流静电发生器作为电荷源向试样施加电荷，由于平板电极接地，故电场强度由固体侧指向气体侧，则为负。在气体侧放电前，γ1＞＞γ2，ε1γ2-ε2γ1＜0，σ(t)为正，表面积累正电荷；当气体被电离时有γ1＜＜γ2，ε1γ2-ε2γ1＞0，σ(t)为负，表面积累负电荷，与实测情况相符。这一表述也同样可以揭示关于放电前后两个阶段电荷的形成过程。

另外，由式（1）可知，在外界实验条件（气体、电压）和介质材料一定的情况下，因式U(ε1γ2―ε2γ1) /(Aγ2+Bγ1)和τ0均为定值，且不影响函数的单调性，令U(ε1γ2―ε2γ1)/(Aγ2+Bγ1)=δ，则函数σ(t)/δ=1-可大致描述函数的变化趋势。为了更好地描述σ(t)与时间的变化关系，可对某一介质表面的电荷变化函数可进行归一化处理，即：

图1 是经归一化后处理后表面电荷密度变化曲线。由图1 可知，电荷密度呈现出先快速增长再逐渐放缓的趋势。介质表面电荷密度σ(t)与表面电位u(t)有如下关系[11]：

图1 归一化后的σ（t）理论变化曲线Fig. 1 Normalizedσ（t） theoretical change curve

σ(t)=M·u(t) (3)

式中：M为系数。式（3）表明，电荷密度的变化可由具体结构表面的电位变化来代替，故可以将介质表面电荷的变化等效为表面电位变化。据此，本研究以rGO/CNTs/EP 涂层的表面电位值为主要测量采集数据。图2 为rGO/CNTs/EP 涂层的表面电位值随积聚时间的变化情况。研究发现，在电荷积聚的前10 min 内，所有涂层的表面电位都呈上升趋势，这与文献[8]中理论及实测的结果相符。但rGO/CNTs 添加量为1%和5%的涂层在10 min后出现表面电位值的转折，因此该模型的适用性仍需要进一步讨论。

图2 rGO/CNTs/EP 涂层表面电位变化情况Fig. 2 Potential change of rGO / CNTs / EP coating surface

1.2 复杂过程的理论分析

当电荷积聚的同时又伴随着电荷消散时，可在式（1）的基础上引入一个消散因子e−t/τ1就可得到复杂过程的电荷密度[9]：

式中：τ1为电荷消散时间常数。为了研究式（4）的变化规律，令τ0/τ1=a，代入式（4）得：

同理，令U(ε1γ2―ε2γ1)/(Aγ2+Bγ1)=δ，则σ(t)的变化情况可由σ(t)/δ大致来展现，如图3 所示。对于不同材料a值不同，可以看出，当a→0，曲线相当于图1 中所反映的情况，这说明τ1＞＞τ0，即只考虑电荷积聚的情况。随着a逐渐增大，曲线位置向下移动，电荷积聚对应的峰值逐渐降低，这说明电荷消散的作用在逐渐增强。当0＜a＜1 时，τ0＜τ1，曲线的位置则相对更高，电荷消散速度较慢，因此有一定的电荷积聚效果，特别当0＜a＜0.3 时，σ(t)/δ可达50%以上，电荷积聚作用明显；当a＞1 时，τ0＞τ1，曲线处于低位，积聚的电荷在一定时间内很快消散，表明的电荷积聚效果不明显，电荷消散速度较快。图4 为归一化后，不同a值对应的σ(t)的变化情况。由图4 可见，电荷积聚的速度总是大于消散的速度，并且随着a增大，电荷积聚和消散速度也在增加，综合作用后，由积聚→消散的整个过程很快完成。由此可知，复杂过程中电荷的积聚效果可用积聚时间常数与消散时间常数的比值a来衡量。

图4 归一化后复杂过程中不同a值的σ（t）的理论变化曲线Fig. 4 Theoretical curves ofσ（t） of differentavalues in com plex process after normalization

再由图2 可知，整体上，涂层试样的表面电位值在随时间升高，并且rGO/CNTs 含量为1%和5%的试样随后出现了表面电位值下降的趋势，这与图3 的理论变化曲线在一定范围内一致。相对于电荷积聚模型，上述实验结果与复杂模型的匹配程度更高，其适用性还有待在后续的分析中进行讨论。另外，由于图2 中实验点有限，未能更直观地体现出电位由此之后的走势，需要通过补充实验进一步进行验证。

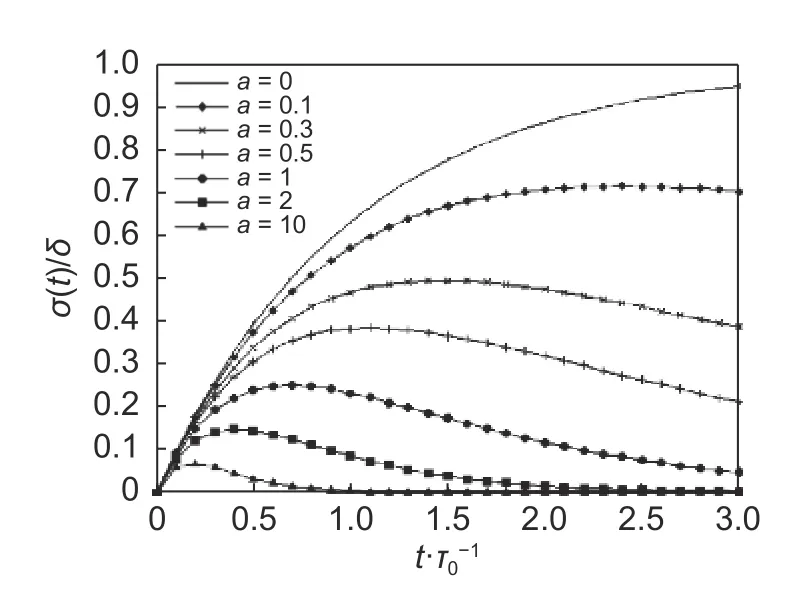
图3 复杂过程中不同a值条件下σ（t）/δ的理论变化曲线Fig. 3 Theoretical curves ofσ（t）/δof differentavalues in complex process

1.3 消散过程的理论分析

当试样的表面电荷积聚到一定程度时，撤掉外界电压后让其表面电荷自然消散，这时试样表面电荷的变化规律可用下式表达[11]：

Q(t)=Q0e−t/τ0 (6)

式中：Q0为初始电荷量；τ0为电荷消散的时间常数，τ0=ε0×εr×ρv，ε0真空中介电常数，εr为相对介电常数，ρV为体积电阻率。由于实验中不易测得电荷量，又U∝Q，因此以表面电位值代替电荷量来研究电荷消散的规律是一种可行的方法。式（7）为试样表面电位u(t)随时间变化的表达式：

u(t)=U0e−t/τ0 (7)

式中：U0为初始表面电位。图5 为归一化后的试样表面电位值的理论变化曲线。由图5 可知，试样表面的电荷消散效果主要受消散时间常数的影响。需要指出的是，自然消散过程中的时间常数与复杂过程的消散时间常数并非取相同值，这是由于两种过程的工况不同，自然消散过程中电荷迁移只与介质材料本身属性有关，而复杂过程电荷迁移不仅与材料属性有关，还受外界电场的作用，这也需要通过进一步的实验和数据分析来进行验证。

图5 归一化后消散过程中u（t）的理论变化曲线Fig. 5 Theoretical curve of u（t） in dissipation process after normalization

1.4 实验方法及数据处理

1.4.1 涂层的制备与测试

先以泡沫镍为基底，利用浸渍的方法制备碳纳米管/泡沫镍复合电极，然后以氧化石墨烯分散液为电泳液，通过电泳沉积的方法在复合电极表面沉积一层石墨烯得到石墨烯/碳纳米管/泡沫镍复合材料，最后通过去除泡沫镍制备石墨烯/碳纳米管(rGO/CNTs)复合材料，并以此为导电填料加入到环氧树脂基体中，制备添加量为0%（纯EP 涂层）、1%、3%、5%的石墨烯/碳纳米管/环氧树脂(rGO/CNTs/EP)复合涂料，在玻璃纤维板上涂覆0.5 mm厚的涂层干膜得到试样。

涂层表面电荷积聚情况的测试方法如下：先将涂层试样经擦拭干净后放在板电极上，并置于测试装置上，将放电针连接到静电发生器作为电荷源，对涂层施加电荷，完成后立即平移到静电测试仪下进行表面电位测量，测试条件为-5 kV，升压速率0.2 kV/s ，持续15 min，测试装置及方法如图6 所示。

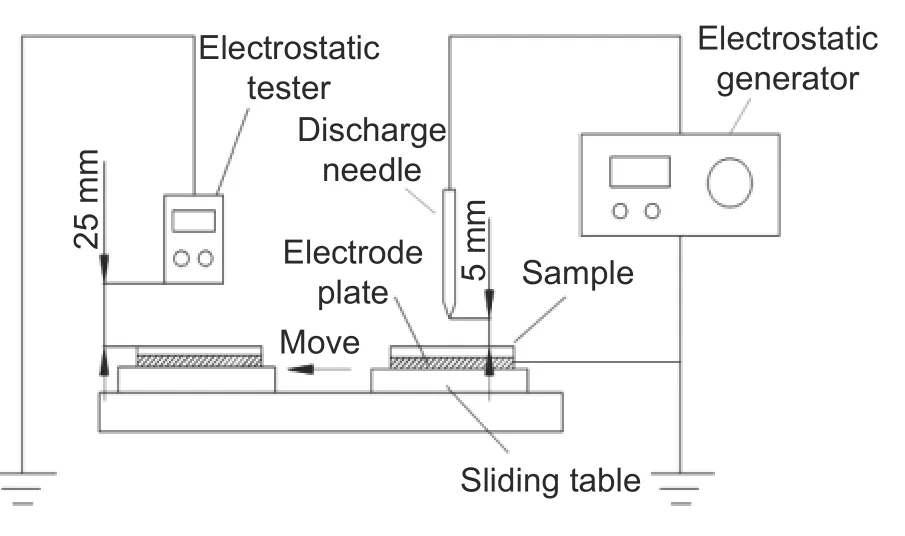
图6 涂层试样表面电荷积聚状况测试装置Fig. 6 Test device for surface charge accumulation of composite coating sample

涂层表面电荷消散情况的测试方法如下：在电荷积聚测试完成后撤掉电荷源，使试样静置在自然状态下进行电荷消散，每隔一段时间进行试样表面电位值的测量。

为了延伸实验数据点，对同一参数下的备用涂层试样（rGO/CNTs 添加量为0%、1%、3%、5%）按照上述测试方法进行电荷积聚测试，测试时间为20 min、30 min，电压为-5 kV。

1.4.2 电荷积聚过程的数据处理

对rGO/CNTs 添加量为0%、1%、3%、5%的rGO/CNTs/EP 涂层表面的电荷积聚实验数据进行拟合，采用的工具为matlab 7.1。如1.1 中所述，研究介质表面的电荷量变化可等效为研究表面电位变化，因此拟合公式分别取为：

u(t)=U·b(1−e−c·t)e−d·t(8)

u(t)=U·b(1−e−c·t) (9)

拟合参数为：外施直流电压U、系数b、积聚时间常数的倒数c、消散时间常数的倒数d及拟合优度的确定系数R2。另，a=d/c。

1.4.3 电荷消散过程的数据处理

对rGO/CNTs 添加量为0%、1%、3%、5%的rGO/CNTs/EP 涂层表面的电荷消散实验数据进行拟合，拟合工具为matlab 7.1，拟合公式为：

u(t)=U0·e−m·t(10)

拟合参数为：初始表面电位U0、消散时间常数的倒数m及拟合优度的确定系数R2。

2 分析与讨论

2.1 电荷积聚过程的数据分析

通过复杂模型（式8）和积聚模型（式9）拟合得到表1 中的各项拟合参数及a值。经比较可得，各组拟合的U基本与外施电压一致，对于EP 涂层，按式8 和式9 拟合得到的各项参数除d之外一致，且τ1=1/d=4.5×1013s，τ1＞＞τ0，说明电荷消散作用极不明显，这是因为EP 涂层的电导率很小，使数据变化规律在该段时间范围内差别不大。对于添加量1%和5%的涂层，式8 和式9 拟合的结果有差距，且有说明式8 拟合优度大于式9，这一点从图7（a）与（b）中拟合曲线与实测数据变化趋势的符合程度比较情况也可看出，复杂模型的拟合结果与实际情况更为匹配，并且拟合曲线走势、位置分布与图3 中的情况相符。 而对于rGO/CNTs 添加量为3%的涂层，按两种模型进行拟合所得的结果基本一致，且τ1＞＞τ0，这与EP 涂层的情况相似。根据3%涂层的电阻率数据可知其与5%的涂层属同一数量级，电荷消散的规律应与其相似，这种结果可能是由于测量错误造成的。综合考虑，复杂模型更好地反映了rGO/CNTs/EP涂层表面电荷的积聚过程。

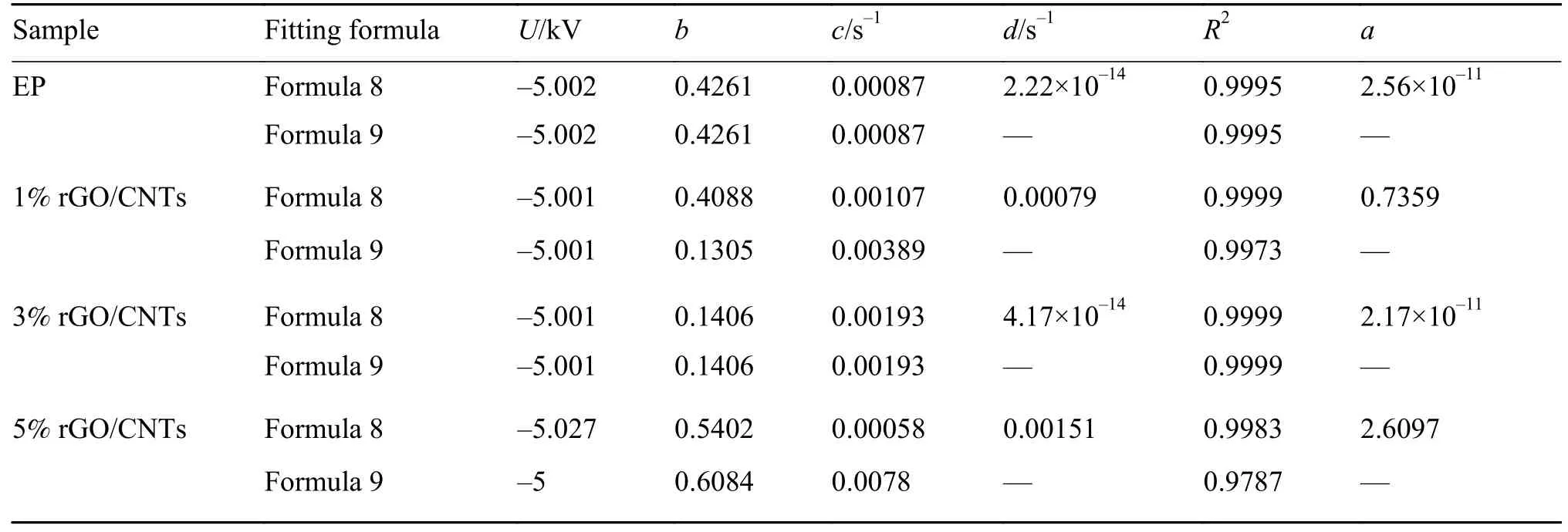
表1 复杂模型、积聚模型的拟合参数及a值Table 1 Fitting parameters of complex model and accumulation model andavalue

图7 rGO/CNTs/EP 涂层在电荷积聚过程中表面电位变化拟合曲线与实测数据变化 （a）复杂模型的拟合结果；（b）积聚模型的拟合结果Fig. 7 Fitting curves of surface potential change of rGO/CNTs/EP coating in charge accumulation process and change of measured data （a） fitting curves of complex model; （b） fitting curves of accumulation model

对比各组的a值可以看出，EP 涂层在10-11数量级，可认为趋于0，随着涂层中rGO/CNTs 添加量的增加，a值也在增加，涂层表面电位的峰值逐渐降低。

图8 为归一化后的表面电位变化曲线，随着涂层中rGO/CNTs 添加量的增加，涂层表面电位很快达到峰值并逐渐下降，EP 涂层基本无下降趋势。对于rGO/CNTs 添加量1%的涂层，经过了700 s左右，其表面电位值由100%下降到80%，对于rGO/CNTs 含量为5%的涂层，则经历了450 s，其表面电位值才下降到相同幅度，这亦说明rGO/CNTs添加量的增大使涂层表面电荷的消散作用得到了增强。

图8 以复杂模型拟合的rGO/CNTs/EP 涂层表面电位变化归一化曲线Fig. 8 Normalized curves of surface potential change of rGO/CNTs/EP coating fitted with complex model

表2 为补充测量的涂层表面电荷积聚20 min、30 min 的电位值。将数据点与图7 中的拟合曲线在该时刻的对应值对比发现，数据点取值与曲线取值基本吻合，表明拟合曲线在反映涂层表面电位变化趋势上是合理的。

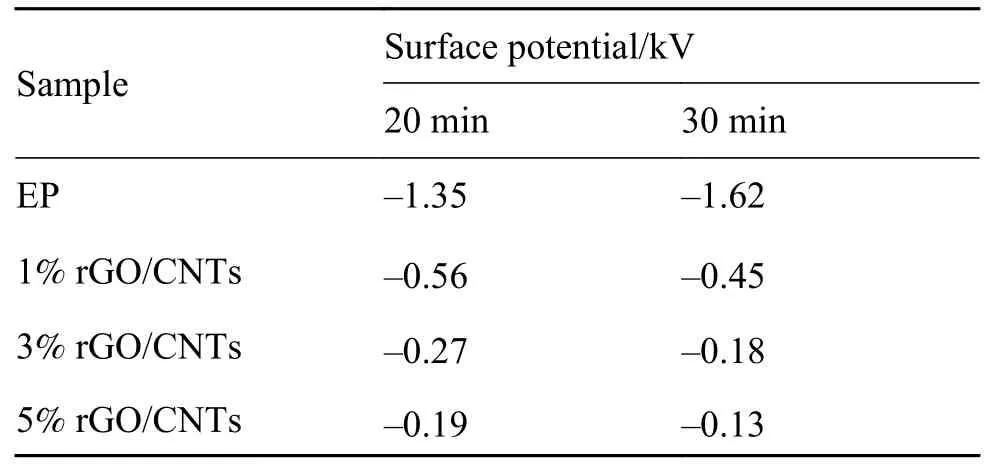
表2 电荷积聚补充测量数据Table 2 Charge accumulation measurement supplementary data

2.2 电荷消散过程的数据分析

表3 为以消散模型（式10）拟合得到的各项参数以及初始电压U0。通过比较发现，拟合的U0基本与实验测得的数据一致，但对于纯EP 和rGO/CNTs 添加量为5%的涂层，其R2低于0.9，拟合优度稍低，这可能是由于在该模型下实验数据点数量有限造成的。图9 为拟合曲线与实验趋势线的对比情况。拟合曲线基本符合涂层表面实际的电位变化趋势，说明该模型较好地反映了实际情况。随着填料添加量的增加，m值逐渐增加，说明电荷消散时间常数τ0逐渐减小，这意味着涂层表面的电荷消散作用得到了增强。

表3 消散模型的拟合参数及实验中的U0Table 3 Fitting parameters of dissipation model andU0in test

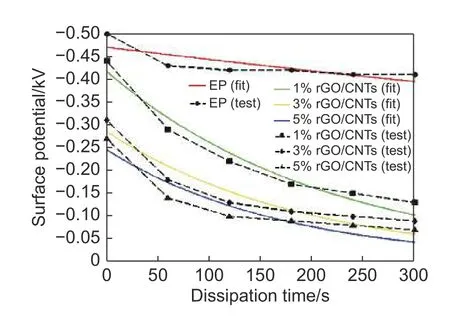
图9 rGO/CNTs/EP 涂层在消散过程中表面电位变化拟合曲线与实测数据变化Fig. 9 Fitting curves of surface potential change of rGO /CNTs / EP coating in dissipation process and change of measured data

另外，从m的拟合值与2.1 中的d值的比较情况可以看出，在复杂模型中的电荷消散时间常数与消散模型中的电荷消散时间常数非同一值，且d值普遍小于m值，这说明复杂过程中电荷消散时间常数大于电荷消散过程的时间常数，即复杂过程中电荷消散作用小于消散过程。由图10 和图8 的对比情况可以看出，图8（复杂过程）中rGO/CNTs 含量为1%和3%的涂层表面电位由100%下降到80%的时间大概在400～700 s，EP 涂层所需的表面电荷消散时间则更长。而图10（消散过程）中，rGO/CNTs 含量为1%、3%和5%的涂层表面电位由100%下降到80%所需的时间基本在40～50 s左右，EP 涂层则需要300～400 s。

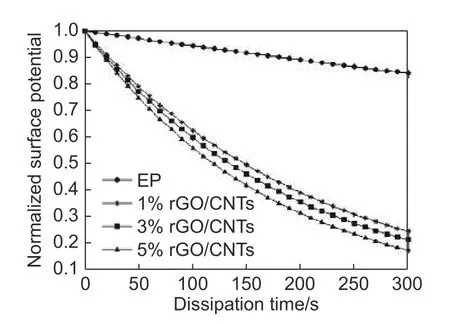
图10 以消散模型拟合的rGO/CNTs/EP 涂层表面电位变化归一化曲线Fig. 10 Normalized curves of surface potential change of rGO/CNTs/EP coating fitted with dissipation model

3 结论

（1） 在涂层表面电荷积聚过程中，通过拟合分析对比了涂层表面电荷的复杂模型和积聚模型，对于rGO/CNTs/EP 涂层，复杂模型拟合曲线与实验点的变化规律符合程度较好；而对于EP 涂层，两种模型差别不大。通过补充测试积聚20 min 和30 min后的涂层表面电位，试样实测数据点基本在拟合曲线附近，证明了拟合曲线在反映涂层表面电位变化规律上是合理的。在复杂过程中，随着rGO/CNTs添加量的增加，a值（积聚时间常数与消散时间常数的比值）增加，电荷积聚峰值下降，电荷消散作用增强。

（2）在涂层表面电荷消散过程中，通过消散模型的拟合分析，拟合曲线基本符合实验数据变化规律，较好地反映了涂层表面电荷消散的情况。消散过程中的时间常数与复杂过程中的消散时间常数非同一值，且复杂过程所需的电荷消散时间大于消散过程，说明复杂过程中的电荷消散作用小于自然状态下的消散过程。

（3）在消散过程中，随着rGO/CNTs/EP 涂层中rGO/CNTs 添加量的增加，消散时间常数减小，消散作用增强。