公务机机翼气动外形优化研究

马晓永，吴军强，肖云雷，张彦军，程志航，秦何军，苗帅

（1.中国空气动力研究与发展中心高速所，绵阳621000）（2.航空工业第一飞机设计研究院总体气动研究所，西安710089）（3.中航通飞华南飞机工业有限公司总体部，珠海519040）

0 引言

近年来，随着世界经济贸易的发展，高端公务机的制造和运营呈突飞猛进势态，尤其是在轻中型公务机领域，以其性能优异、乘坐舒适、性价比高的特点，取得了许多用户的青睐。基于CFD（Computational Fluid Dynamics）的数值优化方法是飞行器气动布局评估和优化设计的有效手段，在飞行器设计方面的作用也愈加明显，数值优化涵盖了数值计算、优化算法和参数化建模方法等内容。飞行器气动外形优化一般定义全机（或部件）阻力系数C为目标函数，在升力系数C、俯仰力矩系数C、机翼（翼型）厚度等约束条件下，通过循环迭代获得目标函数最小值；在进行多点优化时，将不同设计点阻力系数通过加权平均作为总目标函数。研究表明，对于常规布局全机状态，采用传统高精度NS 方程计算方法时，流场求解需占用大量时间，虽然可采用高性能并行计算或基于梯度搜索的伴随方法，但整个优化迭代仍需要大量时间，尤其是在进行多点、多目标优化设计方面。

波音公司全速势方法在流场求解方面具有较高的计算效率，被广泛应用于波音系列飞机的气动外形优化与设计。TRANAIR 软件从20 世纪80 年代开始研发，20 世纪90 年代正式投入使用并成为波音CFD 分析的主要工具，在B777 及B737NG 飞机设计中起到重要作用，并在其后继商业机型气动外形优化设计中大量使用。在TRA‑NAIR 软件中，采用了自适应笛卡尔网格收敛加速技术，不仅可进行流场计算分析，还能进行动导数、颤振特性的快速计算模拟，具有广泛的适用性及稳定性；此外，在进行数值优化时，预留了程序接口以方便进行参数化和约束条件的设置。据统计，仅2002 年该软件在波音公司内部的使用就高达15 000 次，主要用于全机构型的计算与局部优化等。

为了提高某轻中型高速涡扇公务机的总体气动性能，本文以TRANAIR 软件为优化平台，采用类函数/型函数变换（Class Function/Shape Func‑tion Transformation，简称CST）参数化建模及动网格方法，对其机翼进行减阻设计和优化研究，并对优化效果进行分析和讨论。

1 优化模型

优化模型为NAX880 V2.0 轻中型高性能高速涡扇公务机，其几何外形如图1 所示，全机长16.558 m，翼展16.201 m，机翼面积26 m，平均气动弦长2.048 m，典型高速巡航状态的为0.82，高度为10 668 m，雷诺数为1.32×10。

图1 NAX880 V2.0 轻中型公务机Fig.1 NAX880 V2.0 medium business jet

在“机翼、机身、垂尾和平尾”（WBVH）构型下对机翼气动外形进行多点减阻优化，三个设计点参数：C为0.35（其中为0.78，0.80，0.82），高度为10 668 m。WBVH 构型带尾迹计算网格如图2 所示，红色部分为机翼优化区域。

图2 “机翼、机身、垂尾和平尾”（WBVH）构型Fig.2 WBVH configuration（wing，body，vertical& horizontal tail）

鉴于机翼的激波阻力较强，目标函数在阻力系数分解时，提高波阻的加权比例，同时减小诱导阻力和型阻的比重；约束条件为设计点下升力系数、翼型20%（前梁）和80%（后梁）位置最大厚度不减小。其数学模型为

式中：C~C为各设计点下的加权阻力系数。

C=1/2C+1/4C+1/4C（C=0.35，=0.78） （2）

C=10/23C+5/23C+8/23C（C=0.35，=0.80） （3）

C=2/5C+1/5C+2/5C（C=0.35，=0.82） （4）

式中：C为总阻力系数；C为外型阻力系数（型阻）；C为激波阻力系数（波阻）。

机翼上、下翼面变形控制参数和来流迎角为优化设计变量。

2 优化方法

2.1 数值方法

采用基于TRANAIR 软件的笛卡尔网格全速势人工黏性快速数值模拟方法，其中优化方法为基于梯度搜索的序列二次规划（Sequential Qua‑dratic Programming，简称SQP）算法。流场求解后，获得目标函数的梯度信息，与约束条件一起通过SQP 算法转化为非线性优化问题，并通过参数化和网格变形方法实现循环迭代优化设计，直至获得满足约束条件的最优解。

优化算例是在航空工业第一飞机设计研究院曙光计算服务器上进行，性能指标可参阅文献［23］。

2.2 CST 方法

CST 方法是一种包含了传统物理意义设计参数的“类函数/型函数”方法，具体方法介绍和参数设置见文献［23］。针对NAX880 V2.0 公务机机翼优化模型，用130 个CST 参数控制机翼上、下翼面及弯扭，另外三个设计点的来流迎角作为设计变量，一共133 个设计变量。

综上所述，FFD 方法描述的是机翼外形的变化量，当设计变量为0 时作为机翼的原始外形，即当Δ→(，)=0 时→=→，这样就避免了对初始外形直接进行参数化拟合而带来的困难。

采用上述方法对该公务机机翼进行气动外形多点优化设计，整个优化耗时约15 h，共计调用流场计算程序31 次。

3 结果分析

优化前后总阻力参数C对比图如图3 所示，优化前后C、C和C计算结果如图4、表1~表2所示，对比马赫数为0.76、0.78、0.80、0.81、0.82，C=0.35，其中orig 表示优化前的原始外形结果，opt 表示优化后的结果，NS 表示高精度校核。

图3 机翼阻力系数优化结果（CL=0.35）Fig.3 Drag coefficient optimization results of wing（CL=0.35）

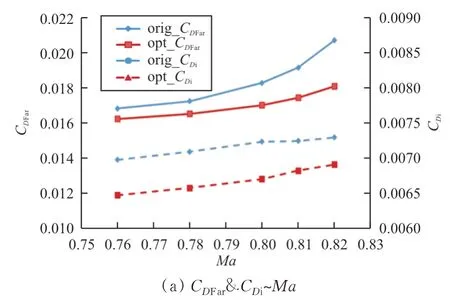
图4 机翼阻力系数分解（CL=0.35）Fig.4 Drag coefficient decomposition of wing（CL=0.35）

表1 优化前机翼阻力系数（CL=0.35）Table 1 Drag coefficient of original wing（CL=0.35）

表2 优化后机翼阻力系数（CL=0.35））Table 2 Drag coefficient of optimized wing（CL=0.35）

从图3~图4 可以看出：随着马赫数的增加，总阻力系数显著增大，优化前=0.78 时C为0.017 2，=0.82 时C迅速增大至0.020 7，阻力系数增加约20.0%；优化后0.78 时C降为0.016 5，0.82 时C降为0.018 1，阻力系数增加量降为9.7%，全机高速阻力整体减小的同时，阻力发散特性也明显得到改善；0.82 时∂C/∂从优化前0.15 减小为0.06，阻力发散由优化前的0.8 提高到0.82 以上。

从表1~表2 可以看出：总阻力系数的改善主要得益于型面阻力系数和激波阻力系数的减小，例如=0.82 时总阻力系数C优化后减小约0.002 6，其中型面阻力系数C和波阻系数C各减小约0.001 1，诱导阻力系数C仅减小0.000 4。

=0.82 优化前后机翼不同展向剖面翼型和压力系数C对比结果如图5 所示。

图5 机翼不同展向剖面翼型和压力优化结果（Ma=0.82、CL=0.35）Fig.5 Airfoil and pressure coefficient ptimization results of different spanwise profiles（Ma=0.82、CL=0.35）

从图5 可以看出：原始机翼为典型的后加载超临界翼型，减阻优化后主要是削弱了激波强度，或减弱和移动了激波位置。结合图4，翼型变化主要反映在翼型中部，优化后上翼面更加平坦。虽然优化后机翼阻力大幅度减小，但也并不是无激波设计，局部区域激波强度甚至稍有增加，这也是多点优化设计中要兼顾不同马赫数情况的原因。

4 结论

（1）本文对轻中型公务机机翼进行了高速状态多点气动外形优化设计，优化后公务机全机阻力系数明显减小，主设计点在优化后阻力系数减小了12.5%；阻力发散特性也得到了显著改善，∂C/∂从优化前的0.15 减小为0.06。

（2）优化方法有效引导了机翼气动外形有利变化。后续将对优化结果开展进一步校核和风洞试验验证研究，进一步提高其工程实用性。