全动翼面间隙非线性气动弹性响应分析
王斐,冉玉国,谭光辉,李秋彦
(航空工业成都飞机设计研究所强度设计研究部,成都610091)
0 引言
全动翼面凭借优良的操纵性和高效的结构形式深受现代战斗机青睐,其操纵系统主要包括转轴、转轴内外轴承、摇臂、作动器及安装支座等部分。在实际工程结构制造与使用中,由于设计公差、生产超差、装配误差及飞机服役过程中运动部件的固有磨损等因素,具有相对运动的不同部件连接处普遍存在非线性因素,由此导致操纵系统刚度具有一定程度的非线性特征,其中最受气动弹性研究人员关注的是间隙非线性。间隙非线性的存在会使基于线性计算理论的气动弹性计算方法不再适用,可能导致结构产生极限环振荡等非线性现象,影响飞机操稳特性及飞行品质,引起结构疲劳问题;同时,间隙问题也将显著影响地面振动试验,使测试结果分散性较大,如F-22 控制面的地面振动试验中出现了间隙非线性现象。因此有必要开展间隙非线性对飞机气动弹性特性的影响分析研究。
美国F-16A 战斗机外挂构型在试飞中出现了极限环振荡现象,研究表明其可能为间隙导致,此后间隙非线性越来越受到颤振研究人员关注。根据型号设计经验,工程上对全动翼面操纵系统的间隙影响普遍达成了共识,美国军用规范MILA-8860 和我国军用飞机结构强度规范GJB 67.7A—2008 都对全动翼面操纵系统总间隙值做出了规定,要求必须控制在0.034°以内,以使间隙非线性对气动弹性特性的影响降到最低。
目前国内外关于间隙非线性气动弹性分析方法的研究主要有等效线性化法、谐波平衡法、数值积分法以及动态子结构法等。张伟伟等采用等效线性化方法分析了带有间隙非线性的舵面颤振特性;B.H.K.Lee 等采用谐波平衡法研究了二元翼段的间隙非线性问题;Yang N等基于双协调自由界面动态子结构法,建立了一种适用于多自由度工程结构的非线性动力学建模方法,开展了折叠翼的非线性响应分析,并与风洞试验结果对比;李家旭等针对控制舵结构模型,通过Lagrange 方程获得了间隙非线性气动弹性方程,分别研究了俯仰和扑动方向间隙非线性的影响;章飞等采用时域方法开展了操纵面间隙非线性颤振分析,并与频率描述函数法进行对比。
综上所述,间隙非线性研究主要侧重于分析方法和非线性效应,大部分研究对象为二维低速模型,面向工程应用的复杂三维模型相对较少,对间隙非线性参数研究主要有间隙值、摩擦、预载以及迟滞等因素。
本文面向工程应用,针对战斗机全动翼面开展间隙非线性气动弹性分析。采用虚拟质量线性化模态振型,应用有理函数法将频域非定常气动力转换到时域,求解气动弹性响应,分别研究间隙值、间隙刚度特性以及阻尼系数对结构非线性响应的影响,以期为型号设计提供参考。
1 理论背景
1.1 间隙非线性气动弹性方程
为了提高分析效率,工程上一般将气动弹性方程转换到模态空间下求解,间隙非线性气弹方程可表示为
̈+̇+=(1)
式中:为结构质量矩阵;为结构阻尼矩阵;为结构刚度矩阵;为广义坐标向量;为动压;为气动力系数矩阵;为模态振型。
间隙非线性主要体现在刚度矩阵和模态振型。
1.2 虚拟质量法
为了降低间隙非线性方程的求解难度,采用虚拟质量法线性化模态振型,基本思想是建立一组可以表达全响应域变形的统一模态振型,确保时域积分过程中结构的连续变形。
该方法通过在不考虑间隙的结构模型上施加虚拟质量,建立虚拟质量模态振型,施加位置一般选择在结构间隙环节附近。忽略阻尼项,施加虚拟质量后的结构自由振动方程可表示为
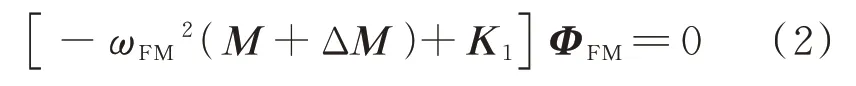
式中:Δ为虚拟质量;为虚拟质量模态振型;为虚拟质量模态频率;为无间隙结构刚度矩阵。
用虚拟质量模态振型替代间隙非线性气动弹性方程中的非线性模态振型,间隙非线性方程可表示为
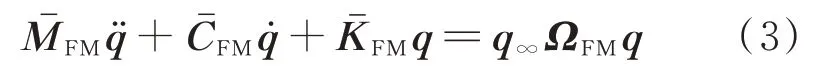
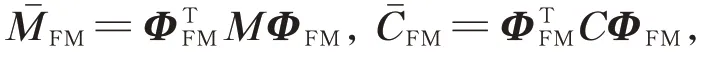
采用虚拟质量模态振型,将结构质量矩阵、阻尼矩阵、刚度矩阵以及气动力影响系数矩阵广义化后,此时间隙非线性方程中的非线性项只有刚度矩阵。
1.3 有理函数拟合
非定常气动力计算采用偶极子格网法,该方法是基于小扰动线性化位势流频域方程的面元法。间隙非线性方程求解需要非定常气动力在时域状态作出描述,通常的方法是以拉普拉斯变量描述的有理函数来近似拟合非定常气动力。本文为获得较高的拟合精度并产生最小的气动力位数,采用最小状态(MS)法进行非定常气动力的有理函数拟合。
MS 法有理函数近似公式为
=+++(-)(4)
式中:为广义气动力矩阵;、、、、为待定系数矩阵;为滞后根矩阵;为无量纲的拉普拉斯变量。
1.4 分析流程
在无间隙模型上施加虚拟质量,通过模态分析,建立虚拟质量模态振型,替代间隙非线性系统的非线性模态振型,对质量矩阵、阻尼矩阵、刚度矩阵以及气动力矩阵进行广义化。非线性系统的响应将非线性系统分成若干线性子系统,采用离散时域状态空间法求解全动翼面的间隙非线性方程。通过给定初始条件,迭代系统瞬态响应和线性子系统,得到每个时间步长内的系统响应,具体流程如图1 所示。
分析流程中间隙非线性气弹方程的离散时域状态空间形式可表示为
{}={}+{}(5)
式中:为结构状态和气动状态矩阵;为外部干扰;为时间增量索引。
矩阵和由式(3)和式(4)联立,引入状态变量可得,包含了非线性系统状态参数,在每个时间步长内根据响应状态更新。
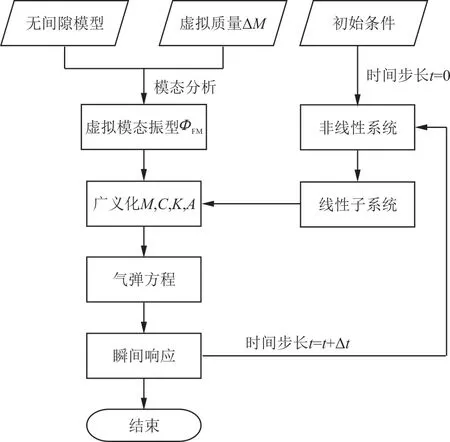
图1 分析流程图Fig.1 Analysis flow chart
2 算例与分析
2.1 模型基本参数
全动翼面基本参数示意图如图2 所示,转轴提供弯曲刚度,翼面法向线弹簧提供旋转刚度,假设模型在旋转方向存在间隙,通过该线弹簧模拟间隙非线性刚度。
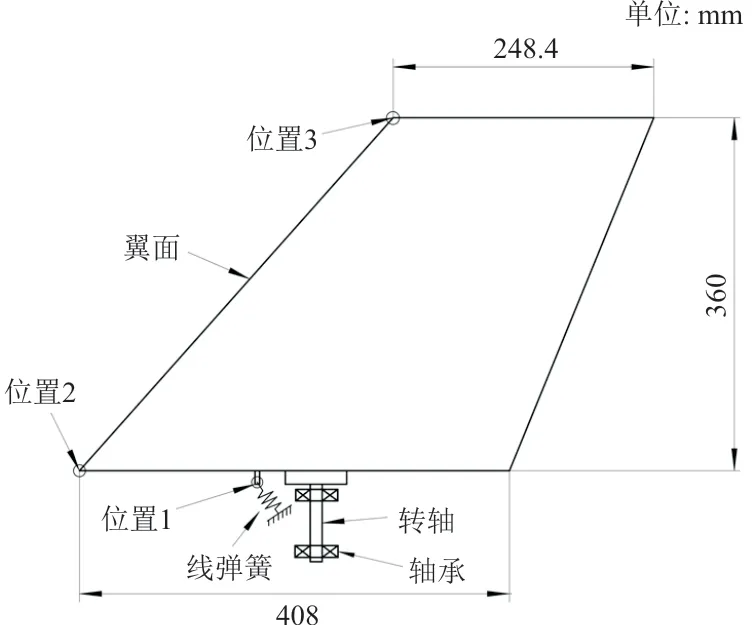
图2 翼面参数示意图Fig.2 Sketch map of wing parameters
本文以双线性间隙为研究对象,如图3 所示,系统刚度是随响应位移变化的非线性参数。当模型位移绝对值小于间隙值时,线弹簧刚度为,当模型位移绝对值大于或等于间隙值时,线弹簧刚度为。翼面采用单梁式结构,翼肋、主梁及蒙皮均采用玻璃纤维复材,梁架间填充硬泡沫,基本参数如表1 所示。
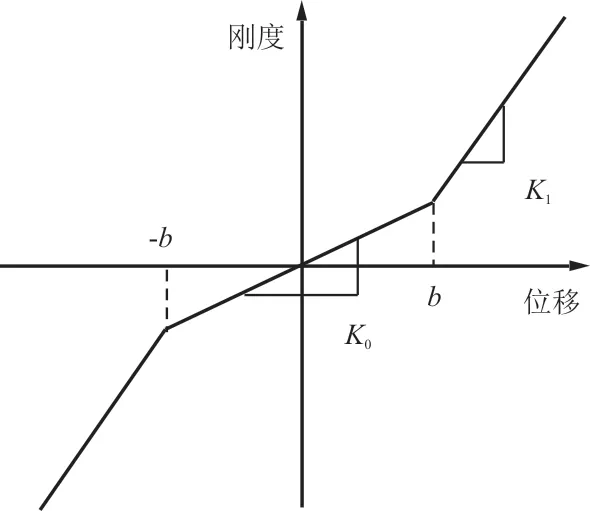
图3 间隙非线性刚度示意图Fig.3 Diagram of nonlinear stiffness of free play
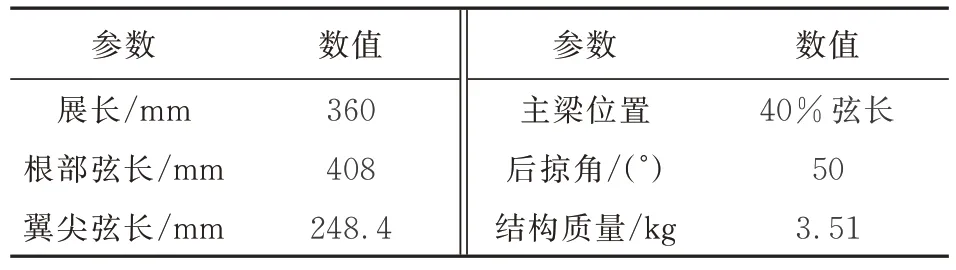
表1 模型参数Table 1 Model parameters
2.2 虚拟质量模态
虚拟质量采用有限元集中质量单元模拟,为了研究虚拟质量大小和位置对分析结果的影响,本文采用5 种虚拟质量,施加位置如图2 所示,线弹簧刚度都取1 100 N/mm,不同虚拟质量大小和位置计算结果如表2 所示,其中~对应位置1,对应位置2,对应位置3。采用这5 种虚拟质量对应的模态振型(Φ,=1,2,…,5),基于频域方法,分别针对线弹簧刚度为0 和1 100 N/mm 的模型(目标模型,无虚拟质量)开展振动和颤振分析,与直接计算结果进行对比,如表3~表4 所示,可以看出:对应的计算结果误差最小,振型如图4 所示。后续分析采用该虚拟质量,其施加于位置1,大小为10 kg,绕重心的旋转方向转动惯量为9.5×10kg·mm;而翼面绕自身重心旋转方向的转动惯量为3.8×10kg·mm,可见虚拟质量的大小与模型在同一数量级即可。
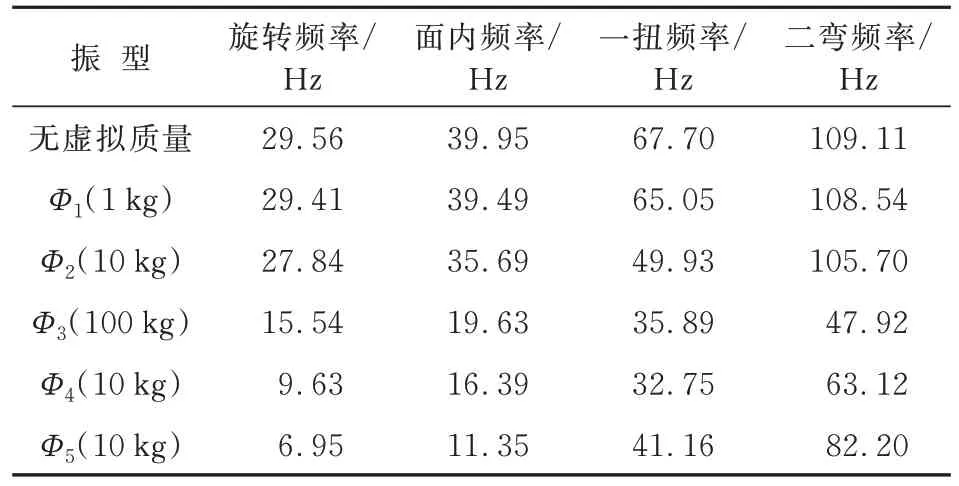
表2 不同虚拟质量模态频率计算结果Table 2 Calculation results of mode frequencies with different fictitious mass
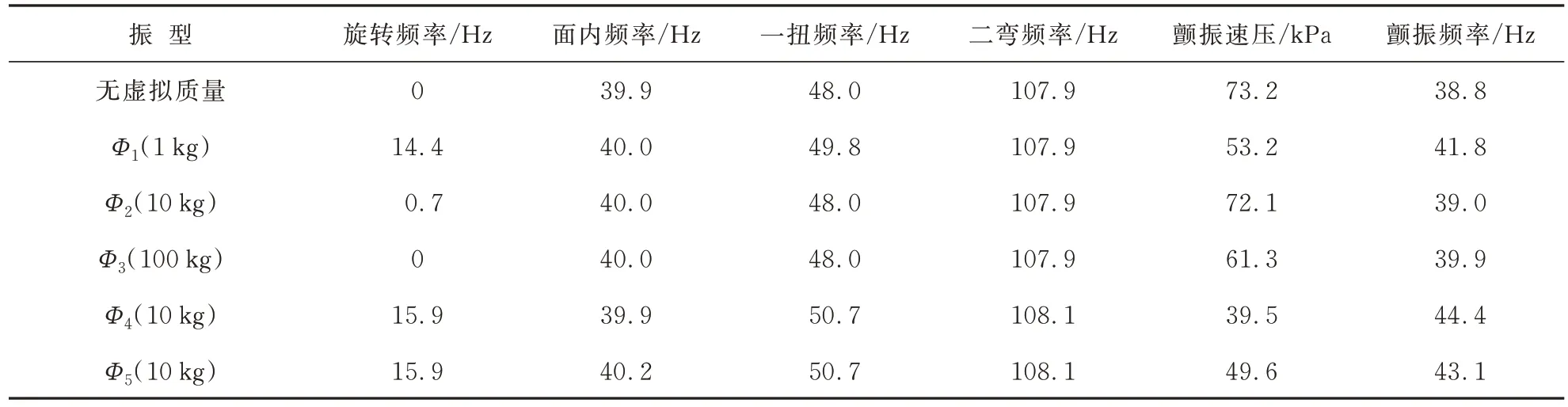
表3K=0 N/mm 下不同虚拟质量模态振型计算结果Table 3 Calculation results with different fictitious mass modal shape atK=0 N/mm
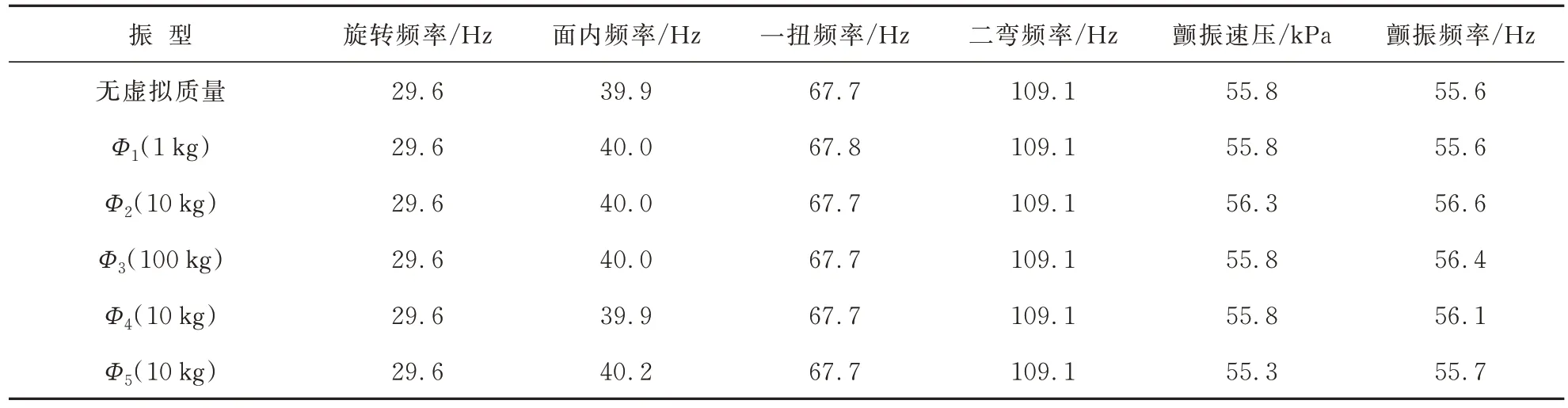
表4K=1 100 N/mm 下不同虚拟质量模态振型计算结果Table 4 Calculation results with different fictitious mass modal shape atK=1 100 N/mm
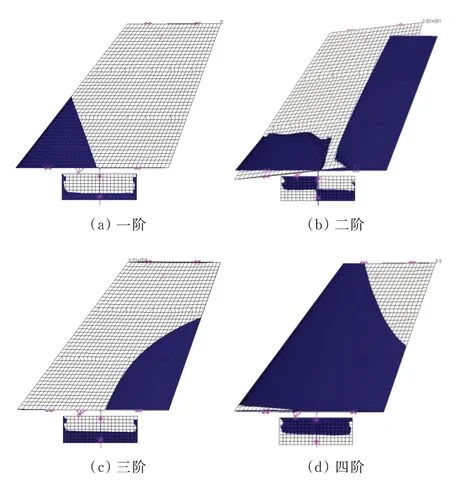
图4 考虑虚拟质量的典型模态振型图Fig.4 Typical modal shape considering fictitious mass
2.3 间隙非线性瞬态响应分析
为了与间隙非线性分析结果对比,针对间隙值为0 mm,刚度为1 100 N/mm 的状态开展时域线性瞬态响应分析,结果如图5~图6 所示,可以看出:线性时域响应结果有明确的分界线,当速压低于58.5 kPa 时,响应收敛;当速压高于或等于58.5 kPa 时,响应发散。
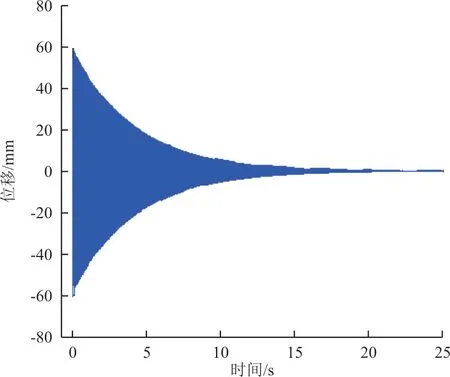
图5 速压58.1 kPa 线性响应结果Fig.5 Linear response result of dynamic pressure at 58.1 kPa
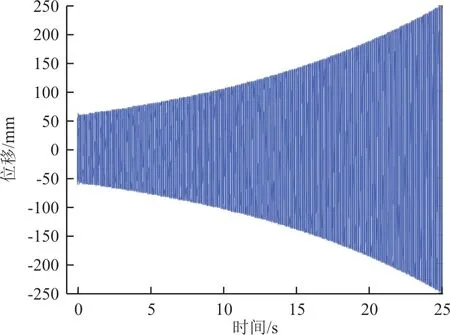
图6 速压58.5 kPa 线性响应结果Fig.6 Linear response result of dynamic pressure at 58.5 kPa
取间隙值为0.5 mm,间隙段内刚度为0 N/mm,间隙段外刚度为1 100 N/mm,以模型翼尖一点为监测点,研究间隙非线性对气动弹性响应的影响,仿真结果如图7~图12 所示,本文仅截取了稳定段时域结果,可以看出:与线性时域响应结果不同,当速压达到46.3 kPa 时,模型动态响应逐渐进入等幅振荡,幅值不随时间变化,相轨迹图呈环形,振动频率固定不变,系统表现为极限环振荡;随着速压增大,系统运动保持等幅振荡;当速压达到58.5 kPa 时,模型响应发散,发生颤振。间隙型非线性会导致系统在速压小于颤振速压时先发生极限环振荡,运动形式与颤振不同,其振幅不会无限增大,并在一定的速压范围内,维持有限幅值运动,但系统的发散速压与线性分析结果一致,因此间隙非线性不影响系统的发散速压。
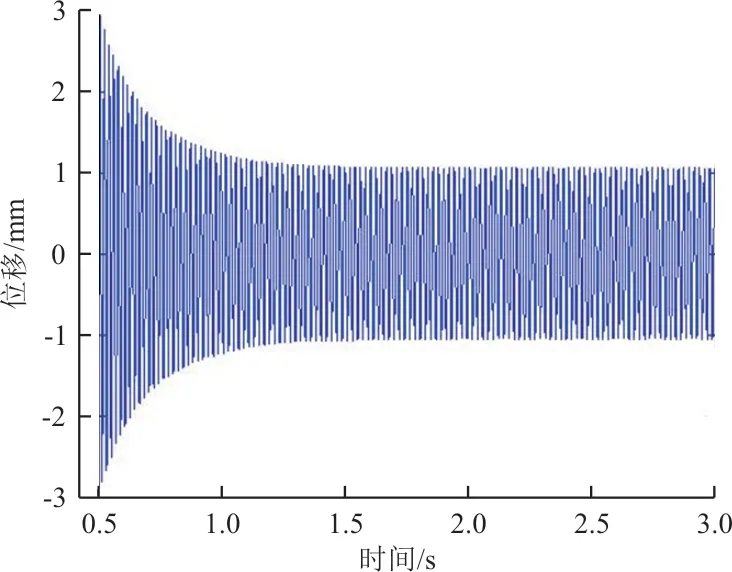
图7 速压46.3 kPa 非线性响应结果Fig. 7 Nonlinear response result of dynamic pressure at 46.3 kPa
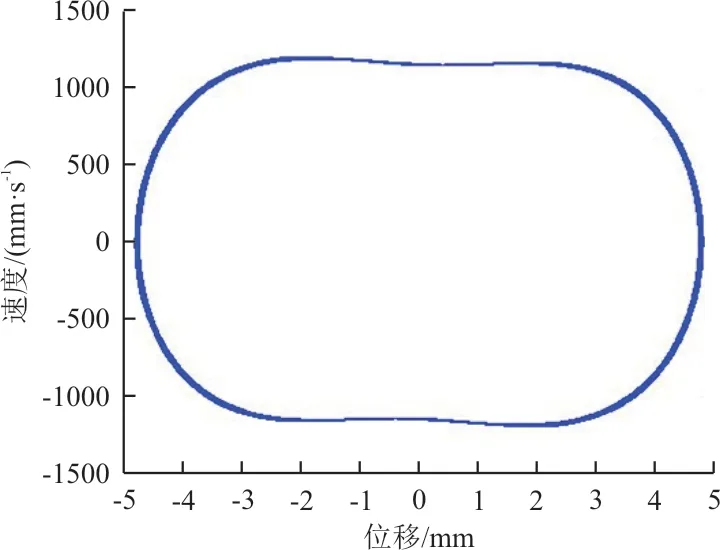
图8 速压46.3 kPa 相图Fig.8 Phase plot of dynamic pressure at 46.3 kPa
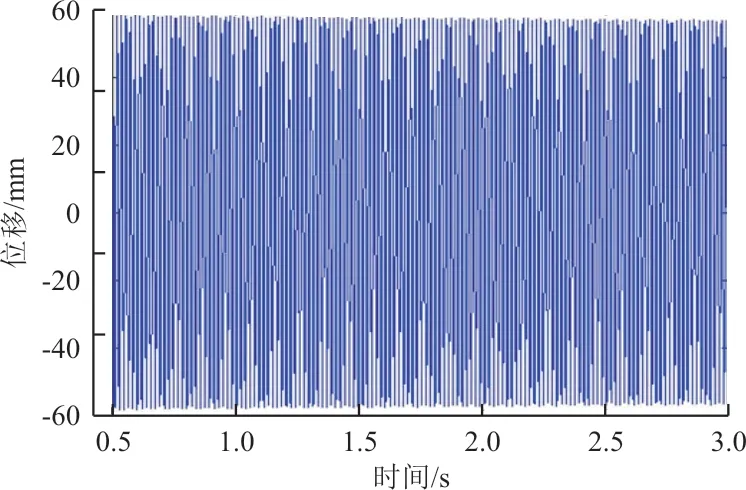
图9 速压58.1 kPa 非线性响应结果Fig.9 Nonlinear response result of dynamic pressure at 58.1 kPa
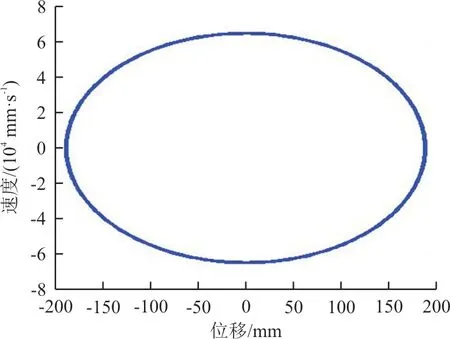
图10 速压58.1 kPa 相图Fig.10 Phase plot of dynamic pressure at 58.1 kPa
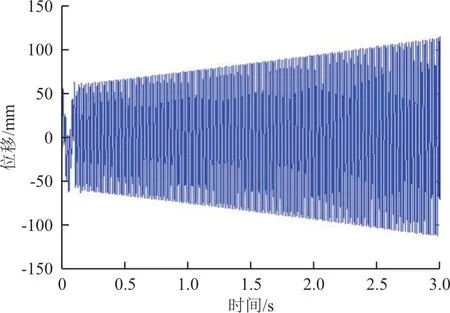
图11 速压58.5 kPa 非线性响应结果Fig.11 Nonlinear response result of dynamic pressure at 58.5 kPa
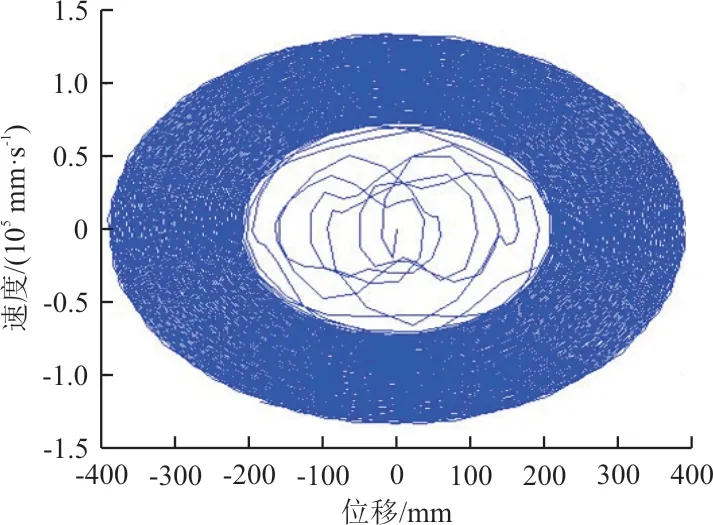
图12 速压58.5 kPa 相图Fig.12 Phase plot of dynamic pressure at 58.5 kPa
2.4 间隙非线性参数研究
等效线性化法是目前工程上普遍采用的含间隙非线性结构动力特性分析方法,本文通过算例与之进行对比。为了研究间隙非线性参数对极限环响应的影响,分别针对间隙值、间隙段外刚度、间隙段内刚度以及阻尼系数等参数展开分析,找出各参数对结构非线性特性的敏感性变化规律。
2.4.1 与等效线性化方法对比
本文方法与等效线性化方法的对比结果如图13 所示,其中间隙值为0.5 mm,间隙段内刚度为0 N/mm,间隙段外刚度为1 100 N/mm。两种方法计算得到的振动幅值随速压的变化趋势基本一致,但同一幅值下等效线性化方法计算得到的速压低于本文方法,主要原因是等效线性化方法为频域方法,间隙非线性刚度采用等效线性化,而本文方法为时域方法,间隙非线性刚度模拟是准确的,但是模态振型和非定常气动力是近似拟合的。因此两种方法计算结果存在差异,但计算结果显示两种方法最大误差不超过5%。
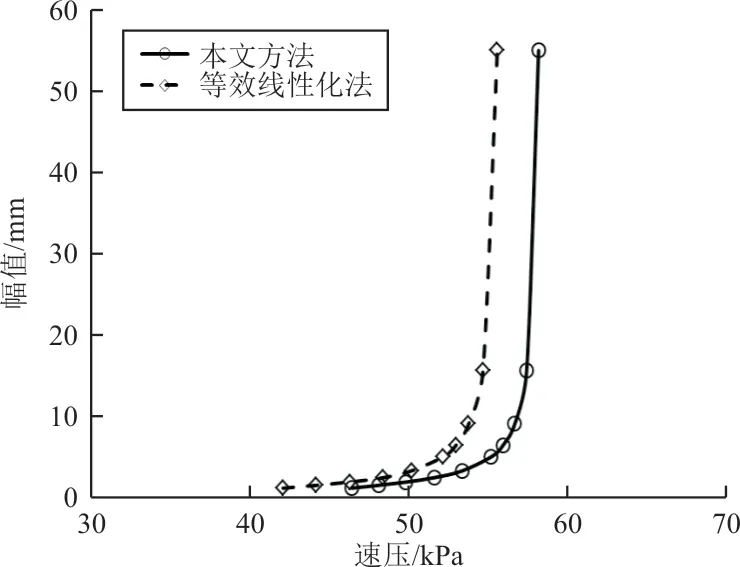
图13 与等效线性化方法结果对比Fig.13 Comparison of results with equivalent linearity method
2.4.2 间隙值的影响
保持刚度值和不变,间隙值分别取0.5,1.0 和2.0 mm,研究间隙值大小对全动翼面极限环响应的影响,仿真结果如图14~图15 所示,可以看出:速压从46.3 kPa 增大到58.1 kPa,三种间隙值对应的非线性系统运动形式都表现为极限环振荡,间隙值大小不影响极限环振荡的进入速压和发散速压;随着速压的增大,极限环振荡的幅值和频率都会增大,且速压越大,极限环振荡幅值的增大幅度越大,但频率变化相对缓慢,与速压近似线性相关,并逐渐趋近于线性颤振频率;相同速压下,间隙值越大,极限环振荡幅值越大,而频率保持不变,可见间隙值大小不影响系统极限环振荡的频率。
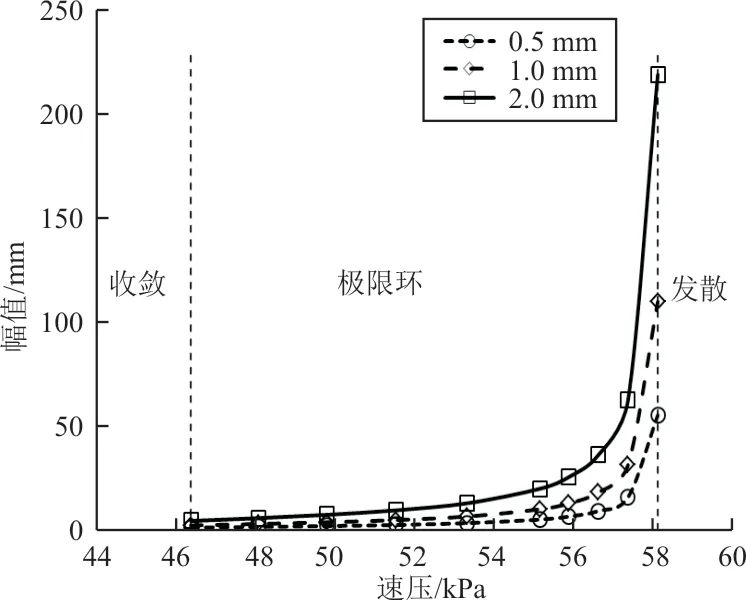
图14 间隙对极限环振荡幅值的影响Fig.14 Influence of free play on response amplitude
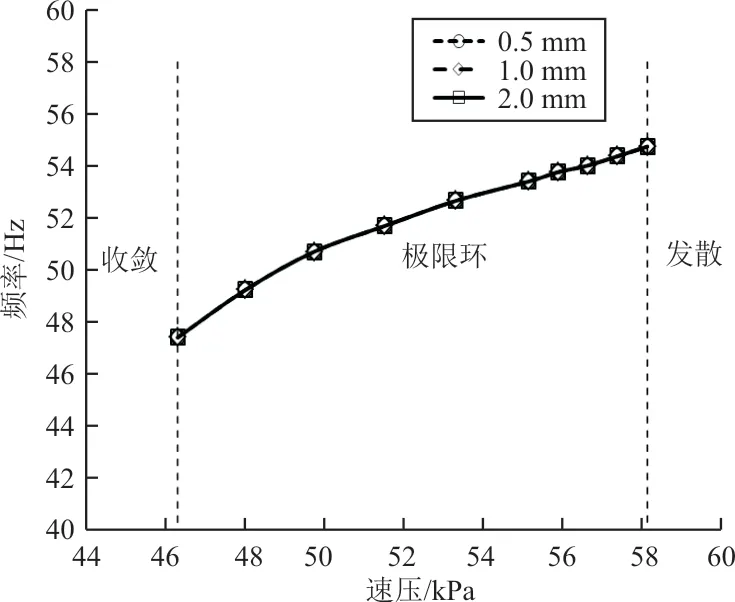
图15 间隙对极限环振荡频率的影响Fig.15 Influence of free play on response frequency
不同间隙值之间的幅值比变化如图16 所示,其中幅值比1 为间隙1.0 与0.5 mm 的极限环振幅比值,幅值比2 为间隙2.0 与0.5 mm 的极限环振幅比值,可以看出:幅值比与间隙值基本保持一致,间隙值增大一倍,极限环振荡幅值也近似增大一倍;相同速压下,单位间隙值对应的极限环振荡幅值基本保持不变。
2.4.3、及阻尼系数的影响
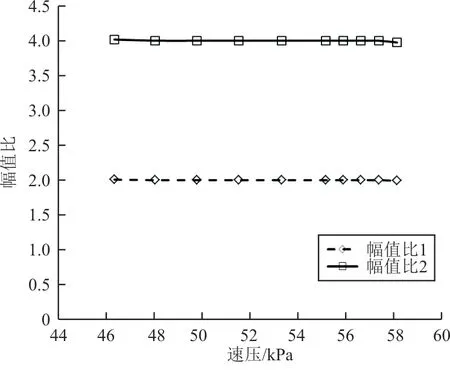
图16 不同间隙条件下的极限环振荡幅值比的变化Fig.16 Variation of LCO amplitude ratio with different free play condition
间隙值保持0.5 mm 不变,分别研究刚度值、刚度值以及阻尼系数对极限环响应特性的影响。
刚度值取1 100 N/mm,刚度值变参结果如图17 所示,可以看出:刚度值只会影响极限环振荡发生的进入速压,不影响系统发散速压;刚度值越大,进入极限环振荡的临界速压越大,当逐渐增大到与相当时,系统变化为线性系统,不再出现极限环现象。
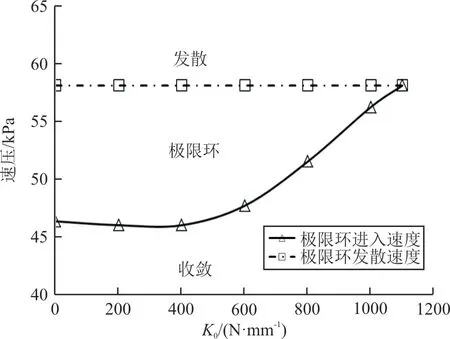
图17K0对极限环响应特性的影响Fig.17 Influence ofK0on LCO
刚度值取0 N/mm,变参结果如图18 所示,可以看出:刚度值越大,系统的发散速压越大,而进入极限环振荡的临界速压基本维持不变,系统出现极限环振荡的速压带越宽,因此刚度值主要影响系统的发散速压,对极限环振荡的进入速压影响较小。
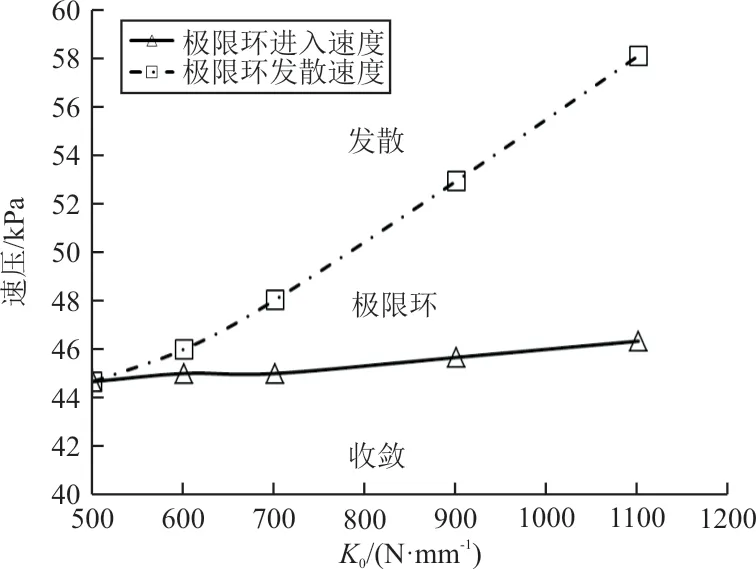
图18K1对极限环响应特性的影响Fig.18 Influence ofK1on LCO
刚度值取0 N/mm,刚度值取1 100 N/mm,阻尼系数变参结果如图19 所示。
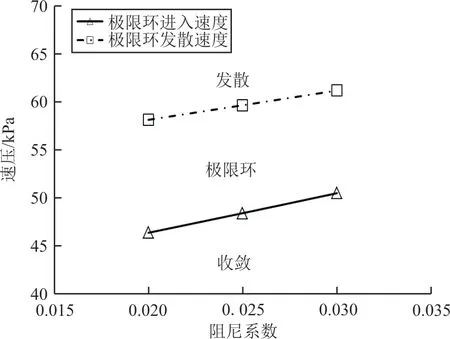
图19 阻尼系数对极限环响应特性的影响Fig.19 Influence of damp coefficient on LCO
从图19 可以看出:阻尼系数主要影响系统的临界发散速压,阻尼系数越大,系统的发散临界速压越大,但不影响系统的极限环振荡速压带宽度,进入极限环振荡的临界速压也随之提高。
3 结论
(1)基于虚拟质量的非线性气动弹性响应分析方法,考虑非线性刚度的影响,针对复杂工程问题开展非线性结构动力特性或气弹特性分析研究,能够满足工程设计基本需求。本文采用的模态法具有气动弹性方程阶数低的优点,计算过程中当刚度发生变化时,不需要重新建模和计算结构固有模态振型。
(2)通过对全动翼面开展间隙非线性气动弹性分析,并与等效线性化方法进行了对比。当全动翼面结构系统中存在着间隙时,在低于线性颤振边界的特定速度区域,翼面会发生非线性振荡现象,即极限环振荡。
(3)间隙值大小仅影响极限环振荡幅值,不影响极限环振荡的频率和临界速压;刚度值和刚度值分别影响极限环振荡的进入临界速压和发散临界速压,而阻尼系数对两者都有影响,导致极限环振荡速压区域平移。

