衬里复合管液压胀接力的弹塑性有限元研究

陈俊文，练章华，汤晓勇，谷天平 ，施岱艳

1.中国石油工程建设有限公司西南分公司，四川 成都610041

2.油气藏地质及开发工程国家重点实验室·西南石油大学，四川 成都610500

引言

高含硫气田地面集输系统面临的H2S 和CO2等环境下管线腐蚀问题是制约此类气田安全开发的难点之一[1-3]。衬里复合管以其良好的经济性和耐腐蚀性能被广泛应用于高腐蚀性气田的集输管线中[4-5]。衬里复合管的成型方式有多种，其中，液压胀型方式以其显著的成型优点被制造单位广泛采用[6]。液胀压力的大小不仅影响衬管、基管的变形量和残余接触压力（又称紧密度），更是决定胀接成功与否的关键[7-8]。衬里复合管的成型力学原理，就是适度利用衬管材料的塑性变形来实现的。因此，必须科学精确地控制胀接压力范围来指导衬里复合管的生产制造过程。

对于衬里复合管液胀力学控制问题，国内外学者做了大量研究。Updike 等[9]首次提出并使用材料当量屈服强度来代替实际屈服强度进行复合管成型参数计算。吕建斌等[10]根据经典弹塑性力学理论，推导出了双金属管液胀成型压力与紧密度的计算公式。张正潮等[11]使用图解法给出了材料当量屈服强度的推导步骤。唐越等[12]通过有限元方法和实验验证了使用当量屈服强度方法可以提高复合管成型参数计算精度。胡洪等[13]使用有限元方法研究了液压胀形压力与紧密度的变化关系。李兰云等[14]研究了初始间隙对液压成型参数的影响，发现随着初始间隙的增大，衬里复合管紧密度有所下降。杜清松等[15]通过设定双金属复合管有限元模型的几何尺寸、材料模型和加载压力等参数来模拟不同条件下复合管成型过程中的力学特性。Akisanya 等[16]利用变形协调条件来描述实际卸载过程并推导了液胀压力计算公式。Olabi 等[17]使用有限元方法对比研究了不同加载路径对制管参数的影响，得出了最优的加载路径。

以上学者的研究均在一定程度上对复合管液胀成型模型做了假设和简化，其研究成果仍具有重要的参考价值，但是由于复合管成型力学的特殊性：不同材料的弹塑性变形涉及复杂的应力应变过程，以往的理论研究无法准确描述衬管材料液胀成型时的应变强化过程。鉴于此，本文提出采用有限元方法，建立材料的多线性等向强化模型，准确地考虑材料真实的应力应变情况，为精确控制衬里复合管液胀成型参数提供理论依据。

1 液压胀接力学模型讨论

衬里复合管液胀成型过程主要涉及4 个阶段：初始阶段、加载阶段、稳载阶段和卸载阶段。初始阶段衬管和基管之间存在适当的初始间隙，加载阶段将胀接压力pi作用于衬管的内壁，通过衬管的弹塑性变形将载荷传递给基管，使基管发生弹性变形，达到设计压力后进入稳载阶段并稳压一定的时间，卸载后由于基管的弹性恢复将抱紧衬管，在两管之间形成残余接触压力从而完成复合管成型[18]，如图1所示。

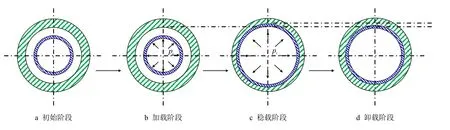
图1 衬里复合管液胀成型过程Fig.1 Hydraulic forming process of lined composite pipe

在进行衬里复合管胀接力学参数计算时，根据复合管结构特点，假设衬管为理想弹塑性材料，将复合管的胀接过程应力应变问题简化为平面应变力学问题，建立极坐标系如图2 所示，其中：Ro—基管的外径，mm；Ri—基管的内径，mm；ro—衬管的外径，mm；ri—衬管的内径，mm；R—基管的中性层半径，mm；r—衬管的中性层半径，mm；δ—基管和衬管的间隙，mm；θ—目标点与x轴之间的夹角，（°）。

基于Tresca 屈服准则，使用Lamé 公式和卸载阶段衬管基管的协调变形关系，推导了残余接触压力、胀接压力计算公式[19]。其中，残余接触压力pcr为

胀接压力pi的区间为

式中：

El—衬管弹性模量，MPa；

k—衬管外内径之比，

σseql—衬管当量屈服强度，MPa；

σsb—基管屈服强度，MPa；

K基管外内径之比，

µl—衬管泊松比，无因次；

µb—基管泊松比，无因次；

Eb—基管弹性模量，MPa。

式（1）和式（2）的解析解数学模型有效地指导了衬里复合管制造过程的成型压力控制，但该解析方法仍存在两个不足之处：（1）Lamé 公式仅适用于厚壁筒弹性材料，而双金属复合管成型时，衬管需要达到塑性变形才能获得与基管内壁接触的紧密度，该公式的适用性受到了限制。（2）解析法使用衬管材料当量屈服强度σseql来代替不同应变时衬管材料真实的塑性硬化强度，但是针对不同制管间隙和衬管材料时，在液压胀型过程中衬管的变形程度存在明显差异，若仍使用当量屈服强度σseql计算将不能保证计算精度。然而，使用有限元法可以不简化地输入衬管材料的真实应力应变曲线数据，在其液压膨胀和卸载过程中，获得较为准确的应变强化数据以及获得准确的紧密度值。下面将基于材料多线性强化理论和有限元方法来解决复合管成型过程中衬管材料强化问题。

2 材料多线性强化有限元模型的建立

2.1 多线性强化模型的建立

目前在衬管选材方面，316L 材料以其良好的力学性能和耐腐蚀性能被广泛应用于衬管制造中。为了研究不同硬化强度的衬管材料对衬里复合管液压胀型紧密度区间的影响，选取两种316L 材料在MTS 材料实验机上进行拉伸实验测试。两种316L材料的应力应变曲线测试结果如图3 所示。材料1是相对于材料2 较软的一种316L 材料，材料1 应变在前20%以内，其强化应力比材料2 低得多，随后两种材料应力差值缩小。

图3 两种316L 材料拉伸实验下应力应变曲线Fig.3 Stress-strain curves of two 316L materials under tensile test

通过实验测试出两种316L 材料应力-应变曲线后，由于其数据量较大，不便用于有限元分析的材料模式，因此，需通过数据处理，用多段直线段来拟合、逼近实验曲线，拟合后两段直线的连接点即可以代表材料应力应变性能的关键点。在本研究中，衬管膨胀受到基管内壁空间的限制，其应变范围超不过10%，因此，仅取了两种316L 材料实验数据的前10%进行多线性应力-应变曲线拟合，其结果见图4。

根据图4 中多线性应力应变曲线数据可知，随着材料应变的增加，第一段直线的斜率即材料的弹性模量，后面几段直线斜率则依次反映了对应形变程度下材料应变强化能力的大小。依次将图4 曲线中的关键点数据在有限元软件中建立两种316L 材料的多线性材料强化模型。

图4 两种316L 材料在应变前10%内的多线性材料应力应变曲线Fig.4 Stress-strain curves of two 316L materials within the first 10%of strain

2.2 有限元模型的建立

以某常用的衬里复合管为例，基管材料为管线钢X70，衬管材料为不锈钢316L，衬里复合管基管规格为ϕ200 mm×24 mm，衬管规格为ϕ148 mm×3 mm，初始制管间隙为2 mm，通过实验测得基管与衬管材料的具体力学参数见表1。根据复合管结构特点和弹塑性力学理论，建立复合管1/4 平面应变有限元模型，施加对称约束。胀接压力pi均匀施加于衬管内壁，设置基管内壁和衬管外壁为接触对，并对接触界面附近的网格进行二次加密，提高接触参数计算精度，如图5 所示。

表1 衬里复合管材料力学参数Tab.1 Mechanical parameters of lined composite pipe material

图5 衬里复合管平面应变有限元模型Fig.5 Plane strain finite element model of lined composite pipe

接触设置方法为：基管内壁为目标面，衬管外壁为接触面，接触单元类型分别为target169 单元和conta171 单元，接触求解方法选择增广拉格朗日法。

2.3 加载—卸载方式

为了使加载过程更加真实地模拟制管加载工况，有限元计算时将加载方式分为10 个分析步，加载—卸载的分析步方式如图6 所示。0∼2 分析步为加载阶段，载荷先从零逐渐线性加载到最大设计值；2∼8 分析步为稳载阶段，保持该内压值一段时间，稳载阶段使得衬管材料处于强化过程的缓冲区，并充分与基管内壁贴合，符合实际制管过程中的加载方式，提高计算结果的可靠性；8∼9 分析步为卸载阶段，将压力值渐线性卸载到零；9∼10 分析步为卸载后阶段，此时内压力卸载为零，基管的弹性回弹将抱紧衬管，使得衬管和基管之间存在一定的紧密度。

图6 有限元模型加载—卸载方式Fig.6 Load and unload mode of finite element model

3 液压胀接计算结果分析与讨论

3.1 胀接内压极限载荷分析

在有限元计算时，在衬管内逐渐施加胀接压力pi，衬管逐渐膨胀，其材料由弹性变形过渡到塑性变形，并且衬管开始与基管接触，继续增加胀接压力pi，达到pimin时，将pimin载荷全部卸掉，基管的弹性恢复完成刚好与衬管外壁接触，即为胀接压力的最小极限载荷pimin。如果在最小极限载荷pimin之后继续加载胀接压力pi，衬管径向膨胀推动基管膨胀，基管处于弹性变形，按规定制管过程中基管不能进入塑性变形，因此，在有限元模拟计算过程中，可以计算出基管内壁刚好进入塑性变形时的胀接压力pimax，即为胀接压力的最大极限载荷。

当胀接压力pi从0 线性加载到150.00 MPa，其有限元模拟计算结果见图7 中一系列的胀接变形及其基管、衬管（316L 材料1）内的Tresca 应力变化过程。由图7 中计算结果可知：随着胀接压力pi的增加，衬管内的Tresca 应力也逐渐增加，当pi=12.90 MPa时，衬管外壁刚好开始与基管内壁接触，如图7c 所示，衬管内最大Tresca 应力为369.70 MPa，超过其屈服应力299.10 MPa，说明此时衬管已经发生塑性变形。继续增加衬管内壁的胀接压力pi，基管内的应力也逐渐增加，直到pi=130.50 MPa时，基管内壁开始出现塑性变形，如图7d，即其应力超过基管材料的屈服应力522.20 MPa，这是实际生产制管时不允许出现的。因此，制管过程中的最大胀接压力pimax=130.50 MPa。如果继续增加pi，基管内的塑性应力也逐渐增大，直到pi=150.00 MPa时，基管内的Tresca 应力达到610.13 MPa，已经接近其抗拉强度极限值626.80 MPa，此时基管材料接近内压失效，见图7f。

图7 基管、衬管内的Tresca 应力随胀接压力的变化过程Fig.7 Variation process of Tresca stress in outer pipe and liner pipe with expansion pressure

将有限元计算结果中基管内壁和两种316L 材料衬管外壁的Tresca 应力随其胀接压力变化的数据提取出来，并通过计算获得其紧密度分布区间，计算结果分别见图8、图9。

由图8 可知，材料2 衬管和基管开始屈服时的胀接压力分别为12.80 和132.50 MPa，残余接触压力为零的最小胀接压力为125.10 MPa，为了保证成型制管具有紧密度，材料2 的胀接压力范围理论上必须控制在125.10∼132.50 MPa。同理，根据图9的计算结果可知，材料1 衬管和基管开始屈服时的胀接压力分别为12.80 和130.50 MPa，残余接触压力为零的最小胀接力为111.45 MPa，因此，材料1 胀接压力的有效范围为111.45∼130.50 MPa。同时，为了保证基管不发生塑性变形，两种材料衬管内的最大胀接压力分别不能超过132.50 和130.50 MPa。

图8 基管、衬管应力随胀接力的变化曲线（316L 材料2）Fig.8 Variation curve of stress of outer pipe and liner pipe with expansion pressure（316L material 2）

从图8、图9 中制管后的紧密度区的变化还可以看出，在相同初始复合管结构尺寸下，316L 材料2和材料1 的紧密度区宽度分别为7.40 和19.05 MPa，表明相同应变位置衬管材料硬化强度高的，其紧密度区越窄，变窄后不利于制管过程中胀接力的控制，即胀接力的灵敏度控制较差。因此，在复合管生产制造时，相同初始复合管结构尺寸下，选择硬化强度较低的材料（材料1），其紧密度区间较宽，更有利于制管胀接力的设计和控制。因此，建议复合管制造厂家在衬管材料选择时，也应将材料的塑性硬化性能考虑在内。

图9 基管、衬管应力随胀接力的变化曲线（316L 材料1）Fig.9 Variation curve of stress of outer pipe and liner pipe with expansion pressure（316L material 1）

与此同时，复合管制造商也应关注不同批次的材料应变强化参数的差异问题，在进行液压胀型前，必须对不同批次的复合管材料进行力学参数测试和评价，充分考虑材料的硬化强度对制管参数的影响，通过计算确定每一批材料对应的制管参数来指导实际生产过程，提高复合管成型的精度和质量。

3.2 胀接载荷与紧密度的关系

根据本文建立的有限元计算模型，通过大量的有限元计算数据，在有效紧密度范围内建立两种316L 材料胀接载荷同紧密度的关系，并对两者关系曲线进行了拟合，结果如图10 所示。

由图10 可知，在其有效紧密度范围内，紧密度与其胀接力为线性变化关系，对两种材料条件下的有限元计算结果进行拟合，其拟合关系的数学计算式为

图10 衬里复合管紧密度随胀接力的变化关系曲线Fig.10 Variation curve of tightness of lined composite pipe with expansion pressure

式中：

xa—胀接力，MPa；

y1—316L 材料1 紧密度，MPa；

y2—316L 材料2 紧密度，MPa。

根据CJ/T 192—2017《内衬不锈钢复合钢管》的规定，双金属复合管在成型后两管间的紧密度必须大于0.3 MPa，才可正常投入使用。所以当卸除压力后查看基管内壁的管间紧密度状况来确定最小胀接压力值。根据紧密度0.3 MPa 的标准，由图10中316L 材料1、材料2 的紧密度和胀接力关系拟合公式，可得这两种材料的最小胀接力分别为113.38和126.99 MPa。

3.3 有限元解和解析解计算结果对比

对衬管316L 材料1 和材料2 的多线性有限元计算结果和解析解结果进行对比分析，由于解析法使用材料当量屈服强度σseql进行胀接力学参数计算，而有限元法直接使用材料的应力应变曲线拟合后的多线性应力应变数据来进行计算，因此，解析解与有限元计算结果对比分析时，以有限元法计算的结果为基准进行对比。根据上文中解析解计算式（1）和式（2）计算胀接成型参数，经过多次试算后发现衬管材料当量屈服强度σseql的取值对计算结果影响很大，为了验证解析公式的计算精度，分别将有限元计算中两种316L 材料对应应变位置的强化应力数据提取出来，作为当量屈服强度σseql代入解析公式中进行计算，其中，316L 材料1 和材料2对应的强化应力分别为441.2 和493.9 MPa。两种方法的计算对比结果如图11 所示。

由图11 可知，两种材料模式下，有限元计算结果与解析解计算结果基本吻合，验证了解析解的计算精度和准确性。这说明使用解析方法计算复合管成型参数时，若衬管的当量屈服强度取值合理，使用解析法是可以满足复合管成型参数计算的。但是，解析法计算时所需要的关键参数—当量屈服强度σseql是不能直接获得的。目前，求解材料的当量屈服强度最常用的方法为图解法[20-22]。使用图解法求解当量屈服强度的误差是不可避免的，尤其针对不同复合管规格、材料和制管间隙时，材料的应变范围变化较大，图解法的应用受到了巨大的限制。由此可见，使用解析法进行复合管成型参数计算的劣势非常明显。使用有限元方法求解复合管成型参数，不仅能够保证计算精度，而且可以根据计算结果实时调整优化成型参数，提高复合管的成型质量。

图11 两种316L 材料胀接力、紧密度有限元计算结果与解析解计算结果对比Fig.11 Comparison of the finite element results and the analytical results of expansion pressure and tightness of two 316L materials

4 结论

（1）通过有限元分析计算结果可知：当满足衬里复合管成型条件时，选择硬化强度较低的衬管材料，可以增大胀接力范围和紧密度区间，更有利于制管时胀接力的设计和控制。

（2）满足本文结构尺寸复合管的紧密度大于0.3 MPa，该两种316L 材料1 和材料2 的最小胀接力值分别为113.38 MPa 和126.99 MPa，建议复合管制造商应关注不同批次的材料应变强化参数的差异问题，制管前对不同批次的复合管材料进行力学参数测试和评价，及时调整制管参数以保证成型质量。

（3）当衬管材料的当量屈服强度σseql取值合适时，有限元计算结果与解析解计算结果吻合度高。但解析法的缺陷为当量屈服强度σseql取值精度控制较差。

（4）文中建立的材料多线性强化有限元模型，使用材料的真实应力应变曲线拟合后的多线性应力应变数据来进行计算，完整考虑了衬管材料在胀接过程中的应变强化，计算结果更加准确。