深度学习视域下培养学生计算思维的实践研究

宋新波 丁双林 陈智敏

摘要：本文以《数据编码——二进制》一课教学实践为切入口，探寻深度学习视域下培养学生计算思维的路径——创设情境、自主探究、探索原理、解密游戏，并在这一路径中引导学生进行深度学习，以期达到培养学生计算思维能力的目的。

关键词：二进制;计算思维;深度学习

中图分类号：G434  文献标识码：A  论文编号：1674-2117（2022）08-0034-03

随着高中信息技术课程改革的不断推进，如何转变学生学习方式的研究成为信息技术教学研究的热点。新课改强调课堂学习方式从“教师教课文”转向“学生完成学习任务”，着眼于学生信息技术核心素养的发展，这与深度学习的理念不谋而合。为此，笔者以《数据编码——二进制》教学实践为例，基于深度学习理念设计教学活动，旨在探索高中信息技术课堂学生计算思维的培养策略。

为让学生掌握计算机的二进制原理，本节课以学生为主体开展学习活动，教师对学生的学习活动进行引导和帮助，在教学过程中让学生通过自主探究完成基础知识的学习，教师讲解二进制知识的数理原理，帮助学生完成与已有知识的意义建构，逐步提升学习的深度，从而实现学生计算思维的深度培养。本课采取如图1所示的策略模型进行教学。

● 創设情境，激发兴趣

深度学习的核心特征是“活动与体验”，要求学生在教师的引导下进入学习情境，积极主动地提出问题、分析问题并解决问题。所以，本课创设“猜生日游戏”的教学情境，激发学生的好奇心，从而吸引学生参与到教学活动之中。笔者给出如下页图2所示的5张卡片，每张卡片上有16个数，参加游戏的学生说出自己生日的“月”和“日”对应的数分别在哪几张卡片上出现过，基于以上信息，教师能快速说出该学生的出生日期。例如，当某学生回答他生日的“月”在第②④张卡片上出现，而“日”在第①②⑤张卡片上出现时，教师能立即说出他的生日是10月19日。

教师不看卡片就能快速准确地说出答案是游戏趣味性的关键，这充分激发了学生的好奇心和内部学习动机，同时调动了学生参与课堂活动的积极性，为后续教学活动的开展奠定了基础。

● 自主探究，完成任务

教学策略的实施应尽可能还原实际问题的解决过程，通过问题情境启发学生，培养学生自主学习、合作探究等能力，帮助学生深度理解知识。解决问题的过程旨在提高学生分析问题、抽象归纳、建立模型、应用迁移解决问题的能力。基于学习主题将零散的碎片化知识进行深度整合，针对原理性知识教师“适时、适法、适度”讲解，为学生提供必要的帮助，保证教学活动的顺利进行。

为探究卡片上数字的特点，从数字出发，笔者带领学生研究数字出现的卡片集合情况。用5个格子从右向左（最右边格子代表第1张卡片，最左边格子代表第5张卡片）依次表示对应卡片中数字出现的情况，1表示数字在该格子对应的卡片中出现过，0表示未出现。如在上例中，生日的月份在卡片②④中出现过，生日的日期在卡片①②⑤中出现过，填充结果如图3所示。

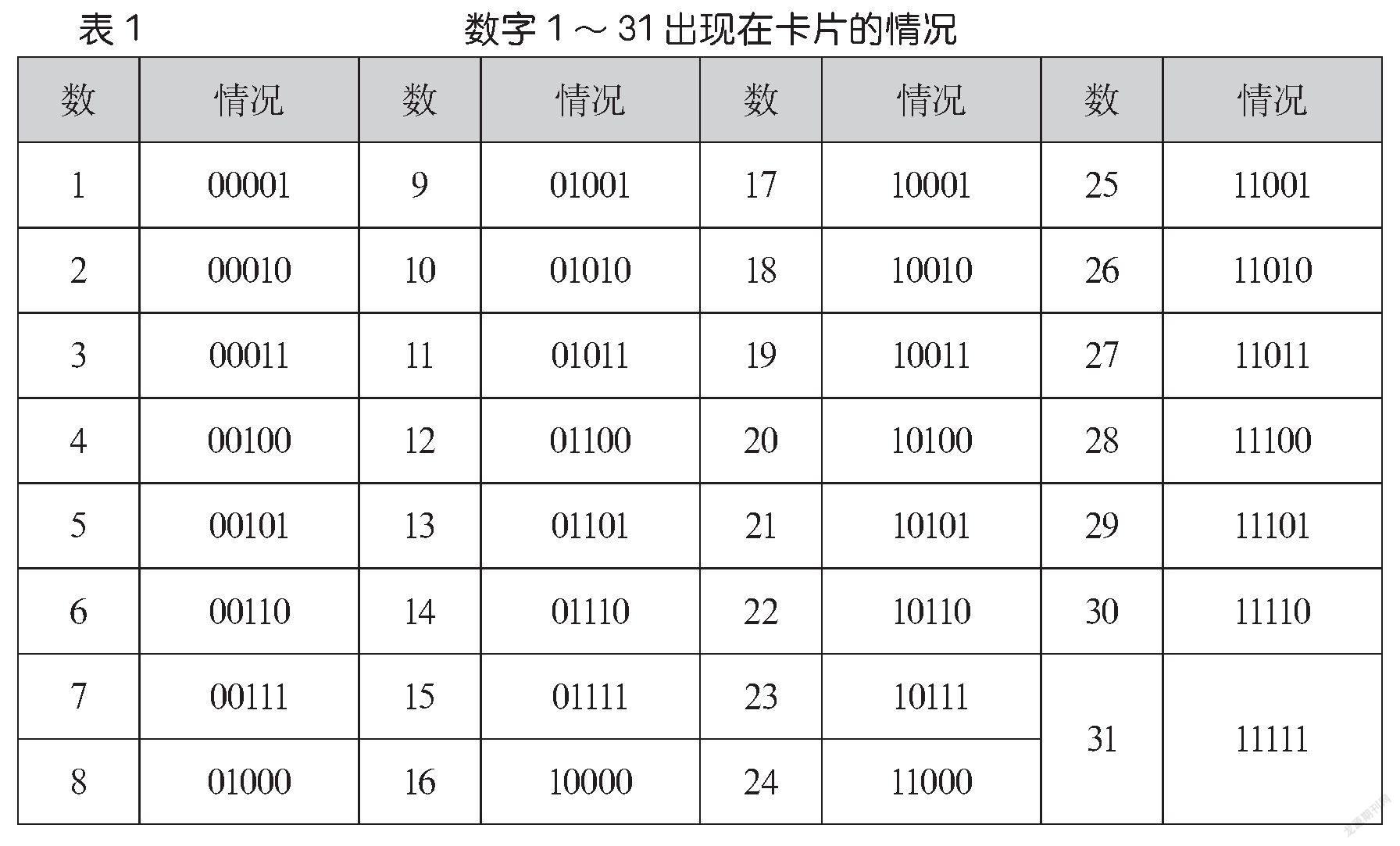
由简单到复杂，由特殊到一般，教师将1～31每一个数字在卡片中出现的情况用上述方法中的01串来表示（如表1），并利用石墨文档实时更新数据的特性，实时了解知道学生的填写情况。从结果可以发现学生已经很好地掌握了以上表示数字出现情况的方法，为后续二进制的学习打下良好的基础。

● 探索原理，深入学习

以上表示1～31每个数字在卡片中出现情况的01串就是二进制。二进制是计算机运算和存储数据的基础，是计算机唯一识别的数字，二进制满二进一，只有0和1两个数字。接下来可以自然地引入二进制的概念，教师提前准备二进制知识的相关材料给学生自学。从熟悉的十进制引入二进制的定义、进位以及位权等知识，再到“二进制数转十进制数”“十进制数转二进制数”等问题，层层递进，环环相扣。

“十进制数转二进制数”是难点，不少教师只讲做法，不讲原理，使得学生对该知识点难以达到“融会贯通，举一反三”。针对这个难点，笔者采用了“除2取余，逆序排列”的方法。具体流程如下：用十进制数除以2，得到商和余数;用上一次除法操作得到的商继续除以2，又会得到新的商和余数。反复执行该过程，直到商为零;将上述过程产生的余数逆序排列即为答案。下页图4是用“除2取余，逆序排列”法把十进制数19转为二进制数10011的全过程。

以上做法的正确性如何证明？因此，课堂上要有证明环节，该环节能让学生掌握二进制背后的原理，从而加深对二进制知识的理解。

● 解密游戏，深化思维

笔者再次安排任务，要求各小组把表1中的01串对应的二进制转为十进制数，并观察规律。大部分小组都能发现：数字x出现卡片情况的01串对应的十进制数就是x本身，即数字x的二进制表示就是x出现卡片情况的01串。这就揭示了卡片设计的奥秘，即把1～31中的每个数转为二进制，把该数放到其所有二进制位上为1所对应的卡片中，如25的二进制表示为（11001）2，则把25放到卡片①④⑤中。

因此，在游戏中，当学生报出自己出生日期所在卡片的全部编号时，教师就能反推出该数的二进制表示。例如，某学生报出其出生日期在卡片②④⑤上出现，则该数的二进制表示为（11010）2。教师可以快速计算出（11010）2=21+23+24=26，也可以把（11010）2看作（10000）2+（01000）2+（00010）2，其中（00010）2（01000）2、（10000）2分别为②④⑤这三张卡片中的第一个数，从而能快速计算出答案。接下来，要求两个学生为一组再次体验游戏，深化对游戏原理的理解。同时，给出拓展任务，设计一个能猜从1900年起包含年份的完整生日的游戏。

● 课堂小测，验证效果

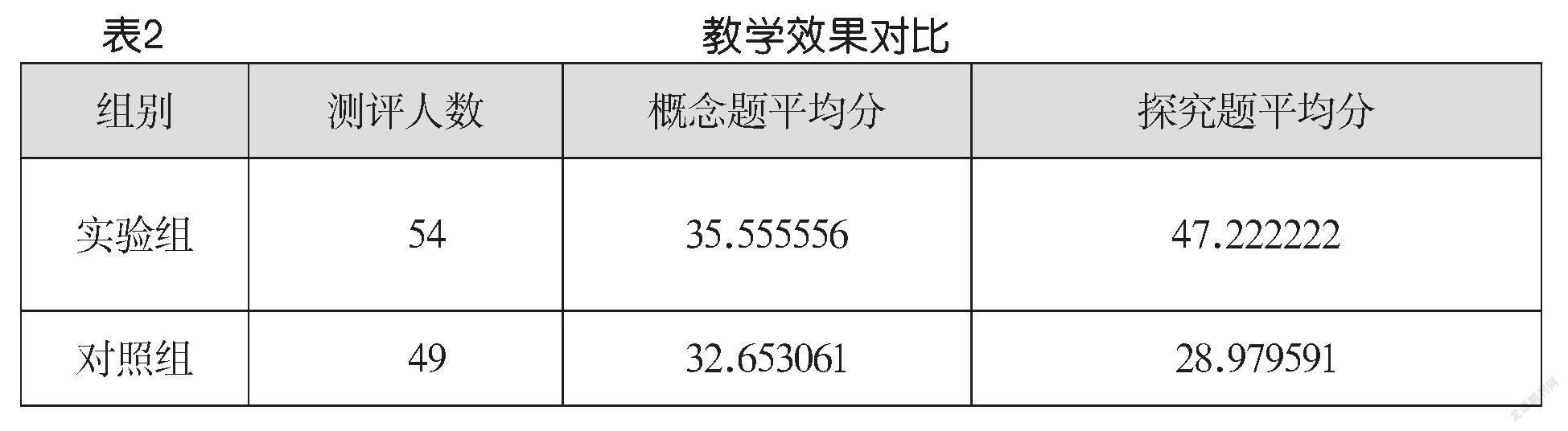
为了验证教学效果，本节课采用了定量的对比试验，根据教学要求编写了有关二进制的习题问卷，共10道题，包括4道概念题，6道探究题，每道题目10分，内容涉及二进制基础、二进制转换、二进制的应用等，考查学生理解、抽象、推理、探究的能力。选取人数相近的两个班级共计103位学生进行实验，其中实验组54人，对照组49人。通过问卷结果（表2）可以发现，概念题模块实验组和对照组平均分相当，但是探究题模块实验组平均分表现更加优秀。

● 对“深度学习”教学理念的思考

以上案例是笔者实践新课标、促进学生深度学习的一次有益尝试，这正是新课标背景下聚焦于提升学生核心素养所需的，因此，教师在教学中要设计真实合理的教学情境，以学生的学习为中心，让学生对知识的来龙去脉不仅知其然，还能知其所以然，真正达到培养学生计算思维和创造性思维能力的目的。当然，真实的课堂教学充满了复杂性和不确定性，在实践过程中还要根据教材内容、学习对象、教师水平等多方面因素进行合理创生，真正把深度学习落到实处。

参考文献：

[1]何玲，黎加厚.促进学生深度学习[J].现代教学，2005（05）：29-30.

[2]曾雪庆，张精宝，吴磊.基于项目式教学提升学生信息素养的实践研究——以《信息技术》课程为例[J].中国教育信息化，2021（02）：56-61.