基于A星算法的无人机高速公路巡检应用研究
靳 朝,林富生,宋志峰,余联庆
(武汉纺织大学 机械工程与自动化学院,湖北 武汉 430200)
0 引言
目前,国内高速公路巡检主要是人工巡检和固定式路测监控设备巡检两种巡检方式:人工巡检费时费力,效率低下且巡检工作人员有安全风险;固定式路测监控设备仅分布在个别重要路段,数量有限[1-3]。此两种巡检方法的低效率、高支出,难以应对复杂地形及恶劣环境,缺乏即时反馈手段,已经难以满足日益加重的高速公路巡检任务。对此,无人机技术作为一种新型技术可以摆脱上述困难,降低环境因素所造成的影响,保证巡查的效率与便捷。
1 无人机航迹规划的实现原理
无人机的航迹规划主要分为4个部分:初始化参数、构建地图、路径搜索、路径优化,如图1所示。
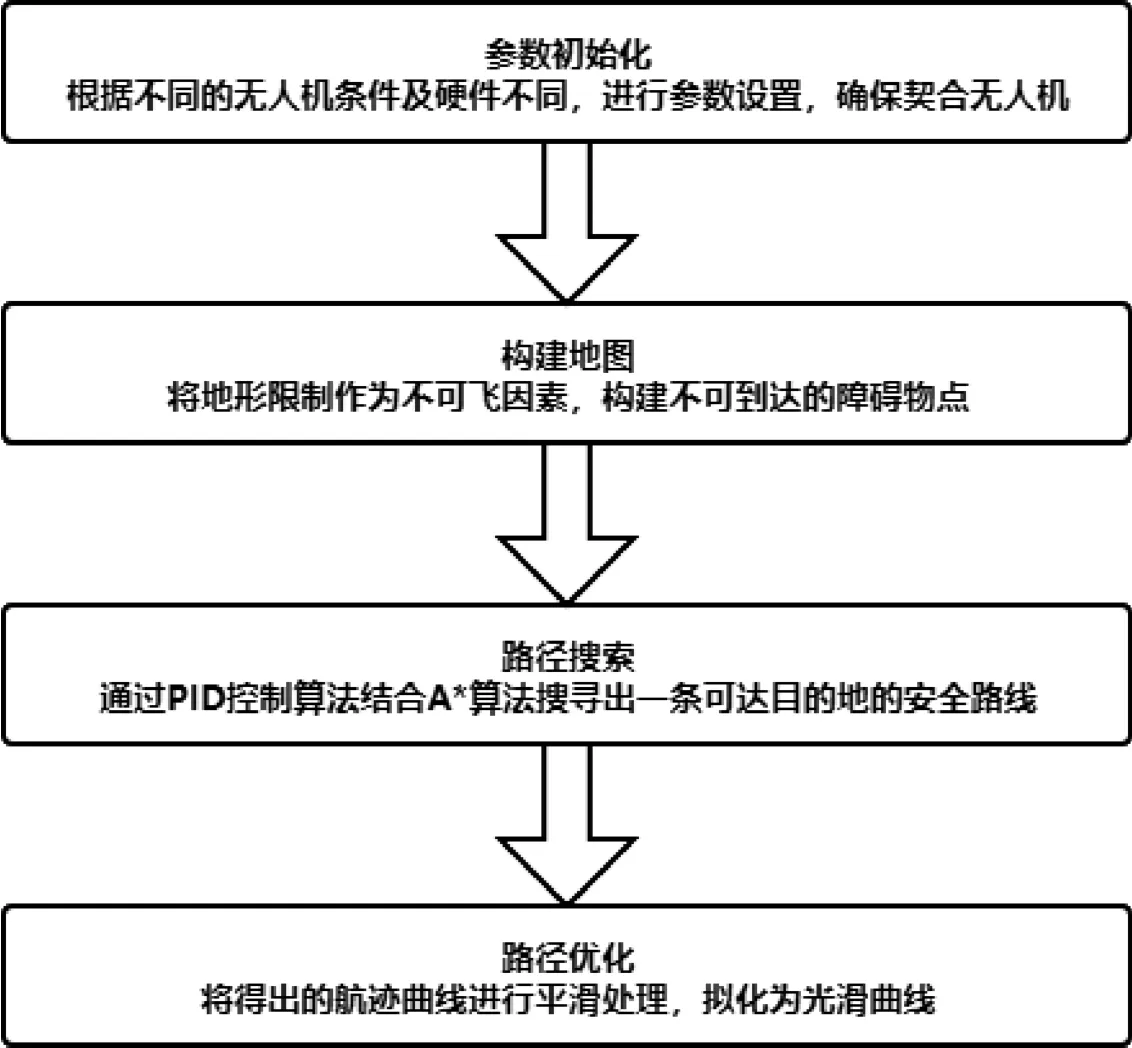
图1 无人机航迹规划技术流程
1.1 参数初始化
在进行无人机自主飞行航迹规划之前需要对无人机进行结构分析和数据估算来确定无人机的约束条件,其约束条件包括最大爬升角、最小步长等。无人机的最大爬升角指无人机的航迹坐标系X轴与水平面之间所能形成的最大夹角,最大爬升角影响的是无人机三维空间的节点划分距离,每一个三维立体节点之间所形成的爬升角必须要小于无人机的最大爬升角。无人机的最小步长是指在当前飞行环境中无人机改变飞行状态所需要飞行的最小直线距离,无人机的最小步长影响的是无人机二维空间的节点划分距离,二维节点间的最短距离不得小于无人机的最小步长。为了简化空间模型,将三维的空间转化为二维空间,消除无人机最大爬升角的约束,所有避障方式全部选择绕飞。
1.2 构建地图
因为采用绕飞的避障策略,所有Z轴方向上的障碍物都可以投影在俯视的XY平面上,在进行空间模型简化后,得到的就是一张二维的空间分布图。为了更加精确地模拟无人机的飞行,使用栅格法构建了一个30 m×30 m的二维空间地图;再根据无人机本身的俯视投影面积大小,来确定无人机的工作区间大小,以确保无人机有足够的飞行空间。
1.3 路径搜索
路径搜索的基本原理就是通过将所需飞行区域简化为方形栅格,方形栅格也就成为了一个二维数组,每一个栅格就是二维数组的一个元素,而这些元素都带有标记,每一个元素都是一个节点,每一个节点都带有可到达或不可到达的标识。在设定好起始点和目标点后,无人机会根据自身所带的摄像模块识别每一个节点所携带的标识,最终再串联带有可到达标识的节点,形成一条路径最终到达目标点。
2 基于A∗(A星)算法的航迹路径规划无人机
A∗航迹搜寻算法是一种作用于搜索区域的启发式算法[4],A∗航迹搜索算法结合于Dijkstra算法和BFS算法,所以它兼具两种算法的优点,不仅能够搜索到最短路径,而且可以使用启发函数。A∗航迹搜寻算法在规划航迹时会对每一个节点进行估值,即:

式中:F(n)指最后经过n个节点所得到的路径;G(n)指从起点出发到达第n个节点所付出的移动代价;H(n)指从第n个节点到达目标点的估算成本。
从起点开始A∗算法会建立一个库,这个库被称为open list。open list作为一个待检查的清单,从起点开始每一个经过的节点周围的所有可到达节点都会进入这个库,反复遍历open list查找F(n)最小值的点,再把它当做处理点,将周围的可到达节点纳入open list,这个处理点会被纳入另一个库close list,当节点进入close list后就不会再被当做处理点,重复上述过程,一直到把目标点纳入open list,即得到一条最优的路径,如图2所示。

图2 A∗算法示意图
图2中,灰色圆点代表起点,灰色三角形代表终点,黑色填充方格代表障碍物,小方块填充方格代表待搜索的open list,交叉线填充方格代表已经搜索过的close list,灰色填充方格代表当前搜索过的路径。
得到路径的过程即估算成本取决于H(n)所使用的启发函数,本文使用的是曼哈顿算法和欧几里得启发算式。
曼哈顿启发函数为:

式中:D表示一个栅格的曼哈顿距离;c代表当前节点;goal代表目标节点。
欧几里得启发函数为:

式中:D表示一个栅格的欧几里得距离;c代表当前节点;goal代表目标节点。
因为欧几里得距离接近两点最短距离,所以得到的路径为最短距离,同时结合曼哈顿启发算法,可以保证路径的稳定性,计算后得到最优航迹路线。
3 基于A∗算法的无人机仿真实验
3.1 环境构建与运行仿真
为了保障算法可以应用于大多数复杂场景下,在模拟场景中将会尽量多地构建不同类型的障碍物。根据无人机的最小步长,将模拟空间平面图构建为一个30 m×30 m的地图,每一个无人机无法到达的障碍点都用一个黑色栅格表示,其他无标注区域均为无人机可活动区域,灰色圆点代表无人机所在位置,灰色三角形代表无人机的目标点,如图3所示。通过运用卡尔曼数据融合技术对各传感器的各项数据进行整合,然后解算无人机的姿态。再运用曼哈顿距离的启发算法对G(n)进行推算,同时通过路径的改变不断地计算出各点的F(n),确保无人机沿G(n)最小值的路径进行移动,最终得出最短路径,如图3所示。
3.2 路径优化
如果通过A∗路径算法搜索所得到的最优航迹路线是一条直线,那么就不用对所得航迹进行路径优化处理。但是在现实环境中飞行航迹不会这么理想化,因此需要对航迹进行平滑处理,而要进行平滑处理就需要消除无人机最大升角和最小步长的影响。本文使用Savitzky-Golay滤波(SG滤波),SG滤波[5]基于局域多项式最小二乘法拟合的滤波方法,其拟合多项式为:

式中:p(n)为拟合多项式;ak为第k个数值;k为数据项数。
其最小二乘残差为:
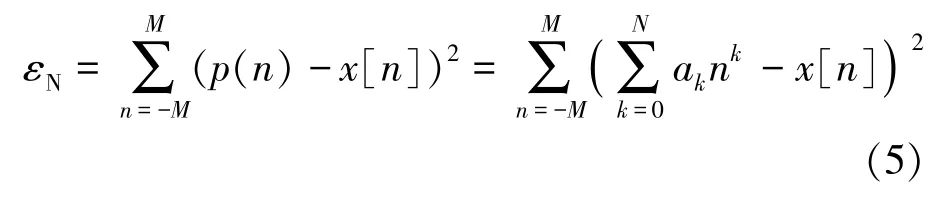
式中:εN为残差期望值;x[n]为给定模型函数。
其运算可以通过卷积运算的方式实现,算式如下:
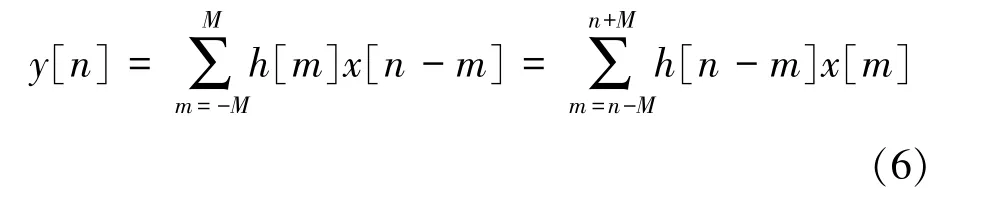
式中:y[n]为滤波后的结果信号;h[n]为滤波系数;x[n]为输入信号;M表示滤波的抽头数;滤波阶数为M-1。
再将所得航迹路线进行平滑处理后得到的路径如图4所示。
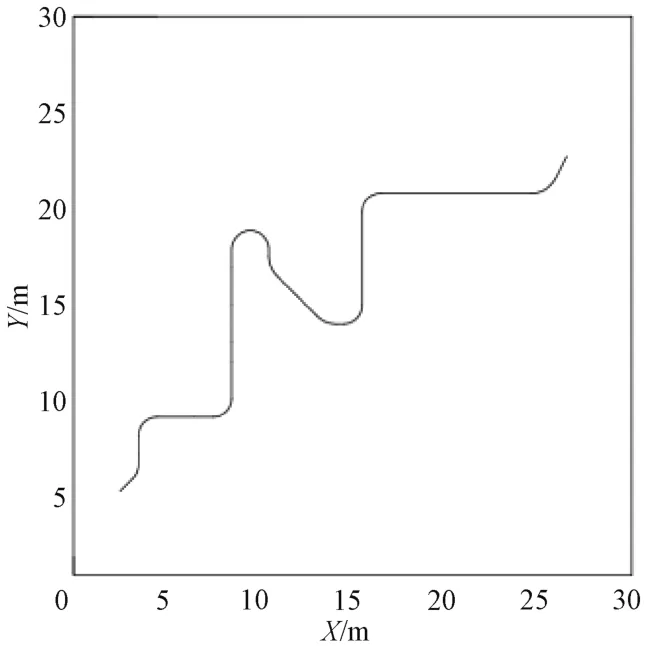
图4 平滑处理后的航迹路线简化图
由图4可以看出,由于对飞行航迹路线进行了优化处理,更加地符合无人机的飞行运动规律,同时因为对每一个转角的平滑处理使得无人机在贴近障碍物飞行时不会因为转折角度问题贴近障碍物的边缘,故以此种寻迹方法进行飞行会降低无人机飞行的碰撞危险性。
4 结语
从上述实验可以看出,基于A∗算法的无人机在较为复杂的环境中可以实现寻迹、避障等操作。针对基于传统人工的巡查方式,本文通过分析高速公路的环境特征、巡查特点,结合无人机技术,对无人机在高速公路巡查的应用进行研究,提出无人机自主飞行高速公路巡查方案。

