基于混合多项式插值的工业机器人关节运动规划
普亚松, 史耀耀, 蔺小军, 张文斌, 陈振
(1.西北工业大学 机电学院, 陕西 西安 710072; 2.红河学院 工学院, 云南 蒙自 661199)
工业机器人广泛应用于搬运、码垛、喷漆、焊接、装配等领域,随着工业机器人技术的发展,工业机器人逐渐用于打磨抛光、监测、自动检测系统等领域,工作性能要求更高,因而对工业机器人运动规划提出更高要求。工业机器人运动规划不仅对末端执行器的位移、速度有着严格的要求,而且良好的轨迹规划还可以保证良好的运动平稳性和较小的机械磨损,提高机器人工作性能[1]。
工业机器人运动规划分为2种类型,一种是作业空间中末端执行器运动规划,另一种是关节空间中关节运动规划。作业空间中末端执行器运动规划,需要反复求解逆运动方程来计算各关节的角位移和角速度,计算量比较大,且有时会出现奇异点,不能正确驱动各关节运动。关节空间中关节运动规划,只需要进行少数目标点位姿与速度的逆运动学计算,极大减少计算量,且不用考虑关节奇异点以及冗余问题,更适合工业机器人点到点的运动[2]。
几种主要的工业机器人关节运动规划方法如下:抛物线过渡的线性规划优势在于线性阶段关节转速保持恒定,但是必须保证有足够的过渡时间,并且角加速度有间断点。三次多项式规划方法简单,计算量少,但对于速度约束的点到点运动,连接点处的角加速度会出现间断点,角加速度不连续,机器臂容易产生颤抖,影响作业性能和使命寿命。五次多项式规划角加速度是连续的,但需要预先设定关节在各目标点的角加速度值,如果设置不当,角速度曲线会出现往复波动现象,不利于关节运动控制。然而,预先设置合适的角加速度值较为困难[3]。并且五次多项次数比较高,角速度曲线和角加速度曲线变化也比较激烈,容易使角速度和角加速度峰值较大[4]。三次B样条曲线也常用于工业机器人运动规划[5-6]。三次B样条曲线用于机器人关节速度约束的点到点运动规划时, 在连接点处角加速度会出现间断点,角加速度不连续。有研究人员对三次B样条曲线进行参数控制,对B样条曲线一阶导数约束的同时,实现了各型值点处G2连续,但并不是C2连续,二阶导数并不是真正的连续[7-8]。
为了进一步解决较复杂的多个目标点关节规划,Niku[9]提出4-3-4多项式样条拼接方法,该方法确保了连接点处角加速度的连续性,但只能指定首、末2个目标点处的角速度,中间目标点处的角速度不能任意指定。Xu等[10]提出3-5-3多项式样条拼接方法,该方法能够任意指定中间目标点处的角速度,并且角加速度是连续的,但是当目标点超过5个时,需要预先设定目标点的角加速度值,角加速度预设定值不适当会引起角速度较大波动。
除了上述方法外,许多研究人员对工业机器人关节运动规划也做了相关研究。田国富等[11]采用内插法替代五次多项式插值对机械臂关节进行连续运动规划,得到C2连续的平滑运动规划,但该方法没有对关节中间目标点的角速度进行约束,无法指定中间点的角速度。施祥玲等[12]采用五次非均匀有理样条曲线(NURBS)对关节运动轨迹进行规划,构造了高阶连续的关节运动轨迹。该方法忽略了NURBS曲线方程可能存在分母项为零的情况,规划曲线有出现突变值的可能性。刘承立等[13]采用三次多项式关节规划,通过把2个目标点按均匀时间划分为5个点,1条规划曲线变为3条规划曲线,得到起点和终点加速度为0的平滑规划曲线,但不能指定中间目标点的角速度。Parikh等[14]采用七次多项式和九次多项式对机器人关节进行运动规划,关节运动路径高阶平滑,关节的速度和加速度连续,但是高阶多项式不仅计算量较大,并且运动轨迹中会产生较大的加速度和速度峰值。
综上所述,对于速度约束的点到点关节运动规划,采用低阶次运动规划方法时,中间目标点的角加速度不连续,会带来附加冲击和振动,影响工业机器人的使用寿命和工作性能。采用高阶次运动规划方法时,虽然解决了角加速度连续的问题,但需要预先设定目标点处的角加速度值。设定合适的角加速度值是个难点,容易引起角速度曲线较大波动。再有,规划方法的阶次越高,运动曲线变化越激烈,角速度峰值和角加速度峰值较大,这些都不利于机器臂平稳工作。本文提出一种三次多项式与四次多项式混合拼接规划方法,对中间目标点的速度进行约束的同时,能够保证中间点处加速度保持连续性,并且角速度波动较小。
1 速度约束的点到点关节运动
工业机器人末端执行器是最终执行元件,是机器人作业的执行器件。末端执行器的运动模式主要有点到点(point to point,PTP)运动和连续路径(continuous path,CP)运动。末端执行器的运动是由机器人各关节共同运动合成的结果,末端执行器的运动和关节有对应的关系。
1.1 关节点到点运动
工业机器人点到点的运动模式适用于点焊、搬运、装卸、电路板插入元件等作业。末端执行器从起点运动到终点,只需规定末端执行器在起点与终点的位置和姿态,起点与终点之间末端执行器的路径和姿态并不作规定与要求。
当末端执行器进行点到点的运动时,工业机器人转动的关节相应地进行点到点的转动。如图1所示,以关节1为例,当末端执行器从起点PA运动到终点PB,关节1相应地从起点A转动到终点B。
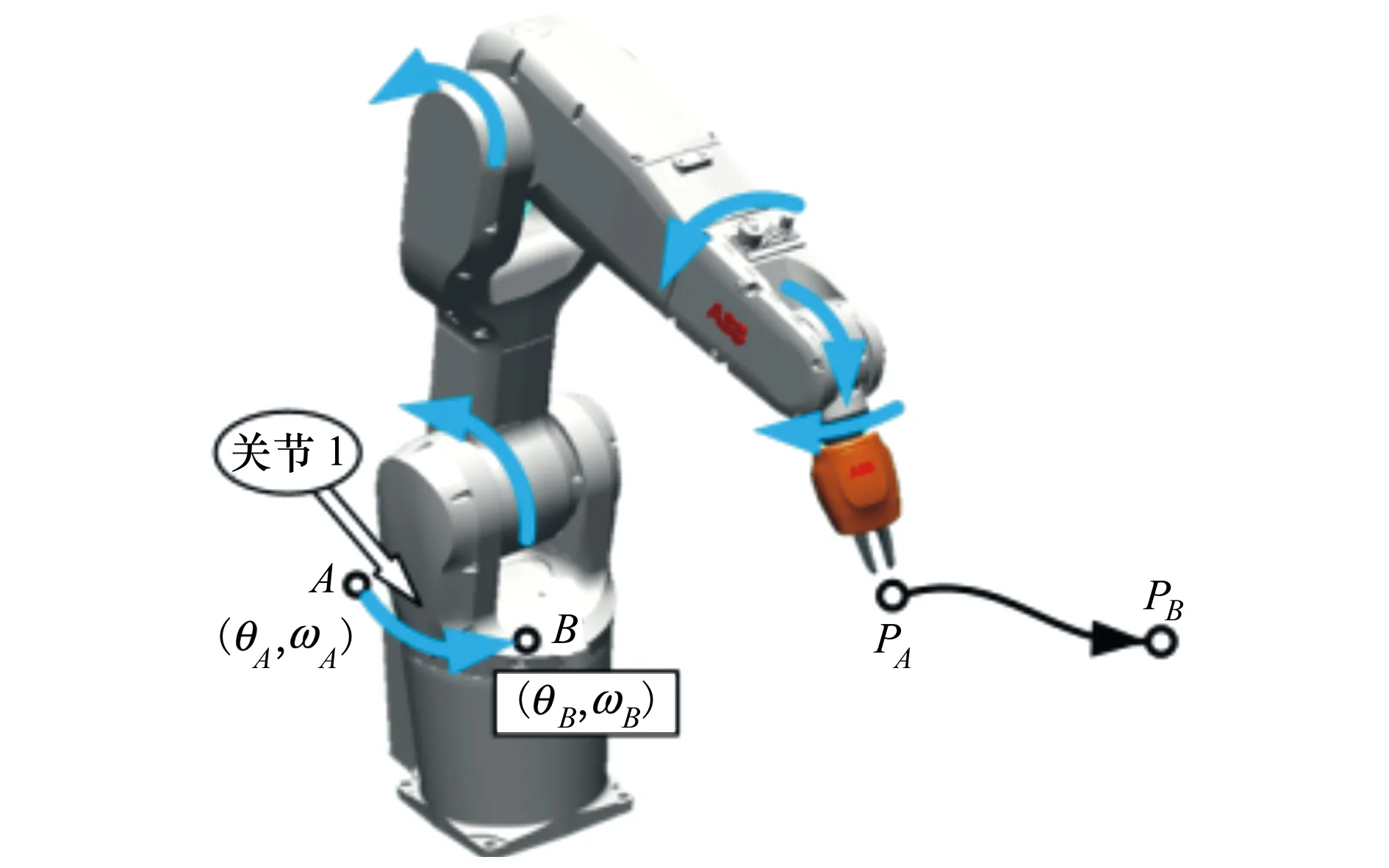
图1 关节点到点运动
末端执行器位姿与各关节角位移具有相应函数关系,如(1)式所示。末端执行器速度与各关节角速度也具有相应的函数关系,如(2)式所示。
式中:[xyzαβγ]是末端执行器的位姿;θi是各个关节角位移;f称为各个关节转角与末端执行器位姿之间的正向运动函数;[vxvyvzωxωyωz]是末端执行器的线速度和角速度;ωi是各个关节角速度;J是速度雅克比矩阵。各种类型的机械臂正向运动函数f以及速度雅克比矩阵J是各不相同的。
根据末端执行器的位姿和速度可以反求各关节的角位移和角速度,如(3)~(4)式所示,称之为逆运动学[9]。
根据末端执行器起点和终点的位姿和速度,通过逆运动学解可求得各关节的起点和终点的角位移值和角速度值,称之为关节起点和终点的边界约束条件。根据起点和终点的边界约束条件,进行各个关节运动规划,各关节运动规划最终合成为末端执行器的运动,流程如图2所示。这种点到点运动模式下,末端执行器在起点和终点的速度都为0,所以各关节对应的起点和终点的角速度也为0,以图1的关节1为例,ωa=ωb=0。
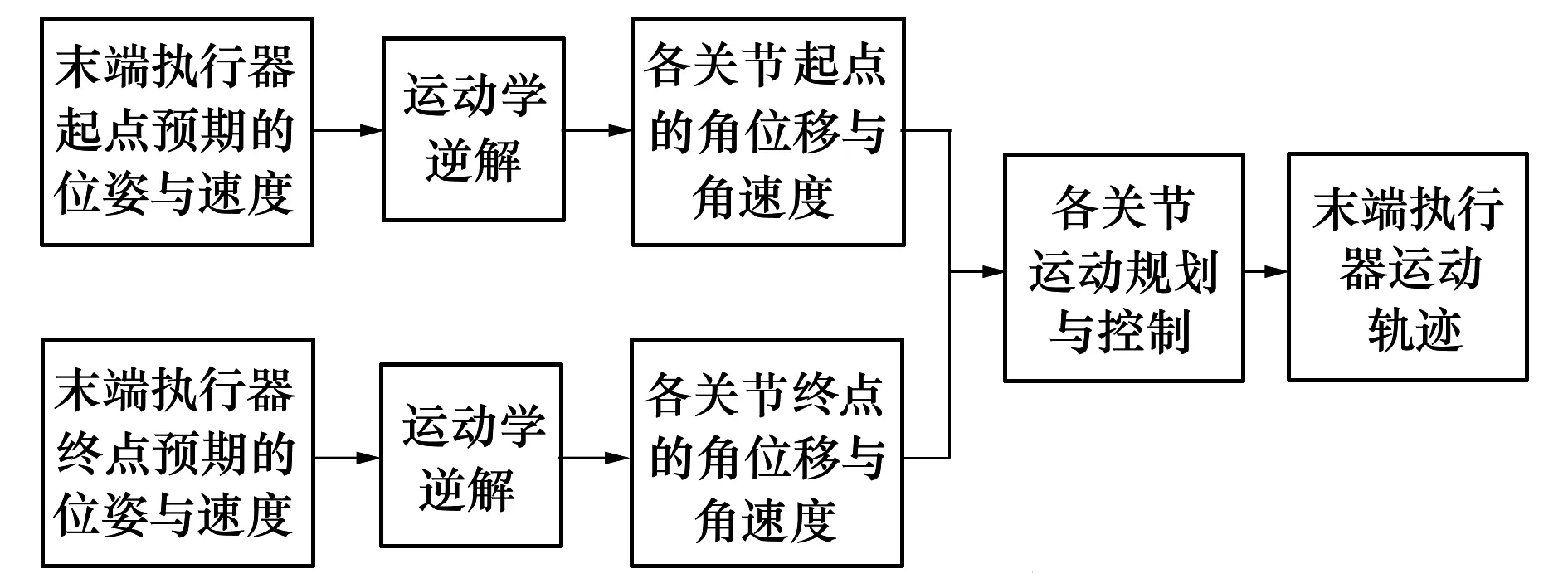
图2 末端执行器点到点运动与关节点到点运动规划
1.2 速度约束的点到点关节运动
当末端执行器点到点运动的起点和终点之间存在多个中间目标点,并且末端执行器需要以规定的速度经过中间目标点,对目标点的位置和速度都要进行约束。末端执行器进行速度约束的点到点运动模式时,各运动关节相应进行速度约束的点到点转动,对关节中间目标点的角位移和角速度进行约束,才能满足末端执行器在目标点处的位置和速度要求。
如图3所示,末端执行器从起点PA运动到终点PD,途中以指定的速度经过2个中间目标点PB和PC,各运动关节要进行相应的转动。以关节1为例,关节1对应地从起点A转动到终点D,途经中间目标点B和C,在中间目标点B点和C点角位移和角速度需要进行约束,角速度值一般不为0,因此,关节1进行的是角速度约束的点到点运动。通过逆运动学求解,可以通过末端执行器的位姿和速度求得关节各目标点的角位移和角速度边界约束条件,就可以对关节1的运动轨迹进行分段规划,对于其他关节也是同样如此,最后各个关节共同合成末端执行器的运动。

图3 速度约束的关节点到点运动
2 关节运动规划方法
工业机器人关节运动规划最常用的方法主要有三次多项式规划、五次多项式规划。
2.1 三次多项式运动规划
多项式插值是一种较为常见的插值方法,用于离散点之间的插值,这与工业机器人点到点运动特点相符合,因此常用于工业机器人运动规划。三次多项式插值是工业机器人关节常采用的一种运动规划方法,三次多项式插值方程如(5)式所示
θ(t)=a0+a1t+a2t2+a3t3
(5)
式中:t为时间变量;a0,a1,a2,a3是三次多项式插值方程的4个系数,需要根据2个目标插值点边界约束条件求解这4个系数。
将初始时间、结束时间以及2个目标点的角位移、角速度约束条件分别代入(5)式及其一阶导数中,经过经整理可以得到求解系数的(6)式。
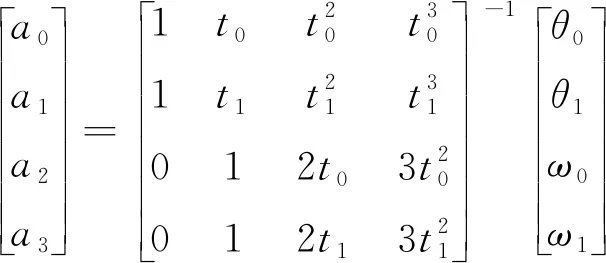
(6)
式中:t0为初始时间;t1为结束时间。θ0与θ1分别为2个目标点的角位移;ω0与ω1分别为2个目标点的角速度,这些值可以通过逆运动学求得。对于普通的点到点运动,ω0和ω1都为0。对于速度约束的点到点运动,ω0和ω1可以不为0。求得各系数之后,就可以得到满足2个目标点边界约束条件的三次多项式规划方程。
三次多项式规划原理简单明了,运算量小,因此广泛用于关节点到点的运动规划。但是,三次多项式用于速度约束的点到点运动规划时,各段规划连接点处会出现角加速度不连续的情况,如图4所示。加速度出现间断点会引起振动和冲击,影响工业机器人的工作性能和使用寿命。
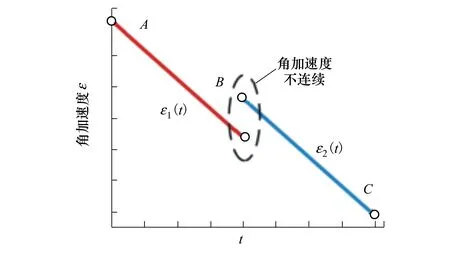
图4 速度约束的点到点三次多项式角加速度规划
2.2 五次多项式运动规划
五次多项式插值也常用于工业机器人关节运动规划,采用五次多项式规划能保证在各规划段的连接点处角加速度是连续的。五次多项式插值方程如(7)式所示
θ(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5
(7)
式中:t为时间变量;a0,a1,a2,a3,a4,a5是五次多项式方程的6个系数,需要根据关节2个目标插值点的角位移、角速度和角加速度边界约束条件求解方程中的6个系数。
将初始时间、结束时间、2个目标点的角位移和角速度的约束条件以及预设定的角加速度分别代入(7)式及其一阶导数和二阶导数中,经过经整理可以得到求解系数的(8)式。
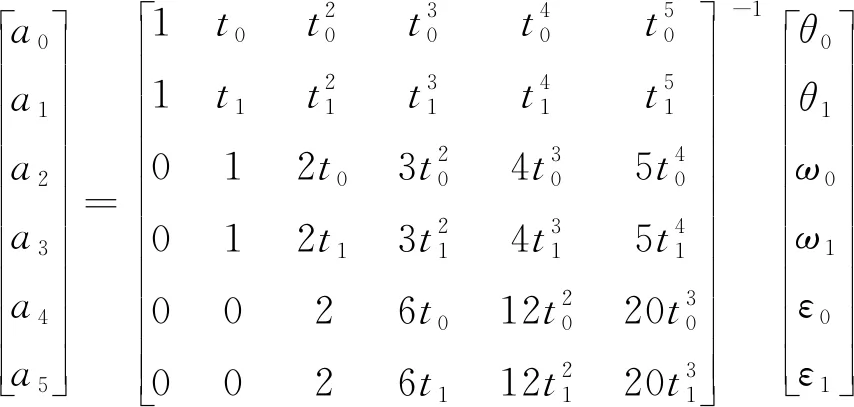
(8)
式中:t0,t1,θ0,θ1,ω0和ω1与(6)式中的物理意义相同;ε0和ε1分别为2个目标点的角加速度,需要预先设定。求得各系数之后,就可以得到满足2个目标点约束边界条件的五次多项式规划方程。从(8)式中可以看出,只要在前、后段规划运动的连接点处设置相等的角加速度值就能保证加速度是连续的。
五次多项式运动规划需要预先设定目标点处关节角加速度的值,如果角加速度数值设定不合适则会引起角速度较大的波动。如图5所示,由于在点A点和B点处的角加速度设定不合适,导致角速度规划曲线ω1(t)′和曲线ω2(t)″出现角速度往复波动,关节电机需要来回加减速,不利于关节角速度的控制。但角加速度要找到合适的预设定值并不容易,因此容易出现角速度波动的情况。
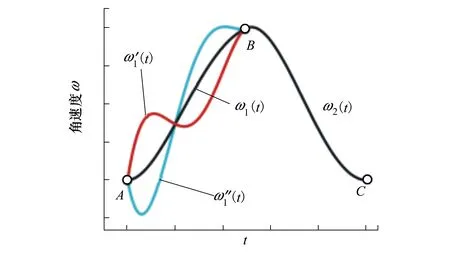
图5 五次多项式规划角速度波动
3 混合多项式插值的关节运动规划
三次多项式规划用于速度约束的多目标点规划时,角加速度不连续,出现间断点。五次多项式规划时角加速度是连续的,但会出现角速度波动大的问题。因此,出现多项式混合插值规划的方法。
3.1 多项式拼接规划
虽然三次多项式规划简单实用,速度平稳,但是单一的三次多项式规划方法显然难以满足工业机器人日益提高的性能要求,于是出现三次多项式与其他多项式混合使用的方法。
Niku[9]提出4个目标点的4-3-4多项式拼接方法用于关节运动规划,该方法可以扩展到高于4个目标点的多项式拼接4-3-…-3-4。这种拼接方法虽然能确保目标点处角加速度是连续的,但是只能指定首、末2个目标点处的角速度,中间目标点处的角速度不能任意指定。Xu等[10]提出3-5-3多项式样条拼接方法,该方法能够任意指定中间目标点处的角速度,并且角加速度是连续的,该方法因为五次多项式的角速度由前后2段三次多项得到,所以不需要进行角加速度的设置。但是当目标点超过5个时,拼接方法成为3-5-…-5-3,此时就需要对五次多项式的加速度进行预先设定,角加速度预设定值不适当时会引起角速度较大波动,角速度运动不平稳。
本文提出的3-4-…-4-4的混合多项拼接方法,可以任意指定各目标点的角速度,确保角加速度的连续性,并且无需预先设定角加速度的值,避免角加速度预设定值不适当带来的角速度较大波动,解决了现有的多项式样条拼接方法存在的不足。
3.2 四次多项式运动规划
本方法运用到四次多项式插值,四次多项式插值方程如(9)式所示
θ(t)=a0+a1t+a2t2+a3t3+a4t4
(9)
式中:t为时间变量;a0,a1,a2,a3,a4是四次多项式插值方程的5个系数,需要根据关节2个目标插值点约束要求求解各系数。
将初始时间、结束时间、2个目标点的角位移和角速度的约束条件以及1个目标点的角加速度代入(9)式及一阶导数和二阶导数中,经过经整理可以得到求解系数的公式(10)。

(10)
式中:t0,t1,θ0,θ1,ω0和ω1与(6)式中的物理意义是一样的;ε0为2个目标点的任意一个目标点的角加速度。这里规定ε0为两个目标点中前一个目标点的角加速度,目的是为了与上一段运动规划的加速度在连接点处相等,也即让加速度在连接点处保持连续。因此,ε0可从上一段运动规划得到,而不需要设先设定,避免角加速度预设定不合适带来速度波动的问题。求得各系数之后,就可以得到满足2个目标点约束边界条件的四次多项式规划方程。
3.3 运动规划时间的计算
关节的运动时间与末端执行器的运动时间是同步、相等的。对于连续路径运动,末端执行器的运动时间等于位移量除以工作运动速度,关节运动时间也等于该时间。对于有时间要求的点到点运动,例如生产流水线分捡、工装等,末端执行器运动时间是根据工作要求而进行设定,关节运动时间也与之同步。
对于没有时间约束的点到点运动,关节运动时间不是唯一的,需要根据一定的条件进行设定。对于关节点到点的运动,目标点中间的速度没有进行约束,如果运动时间非常短,目标点的位移又比较大,过程转动中可能出现关节速度过大,甚至超过了电机允许的最大转速,即“飞车”现象,这是不允许的,因此在关节最大转速小于电机允许的最大转速的前提下,设定合适的关节运动时间。
根据求极值的原理,函数的导数为0处存在极值。对于三次多项式规划方程,二阶导数为0处,其一阶导数存在极值,即角速度存在极大值或极小值,暂且以极大值叙述。根据三次多项规划方程(5),令关节角位移的二阶导数等于0,如(11)式所示,可以得到关节运动出现最大角速度的时间tm,如(12)式所示。
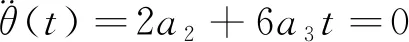
(11)

(12)

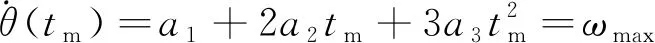
(13)
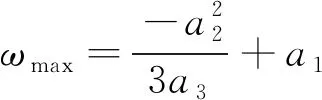
(14)
根据(6)式,系数a1,a2,a3是关于t0,t1,θ0,θ1,ω0,ω1的函数,θ0,θ1,ω0,ω1是已知量。t0是开始时间,对于第一段运动规划t0=0,对于其他运动规划段,t0等于前一段运动规划的结束时间,所以t0是已知量。t1是结束时间,是未知待求量。将系数a1,a2,a3的表达式代入(14)式中,得到(15)式。
ωmax=
(15)

ωmax=

(16)
(16)式中只有t1是未知变量,其他都是已知量,因此可以求解得到结束时间t1。如果从时间效率方面考虑,在电机最高转速范围内,将关节运动的最大角速度ωmax设定得越高,则关节运动结束时间越短,且不会出现因关节角速度超出电机允许的最高转速而引起的“飞车”现象。如果从转动平稳方面考虑,关节最大角速度ωmax越接近2个目标点中较高的角速度,则速度波动越小。结束时间t1随着ωmax变化而变化,可根据不同的需求设定ωmax的值,求解得到相应的结束时间。
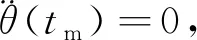
3.4 三次多项式与四次多项式混合插值的运动规划原理
对于速度约束的点到点关节运动规划,本文提出一种三次多项式和四次多项式混合插值进行速度约束的点到点关节运动规划,第一段采用三次多项式规划,其余都采用四次多项式规划,其原理与过程配合图6叙述如下。为了便于描述,把目标点依次标记为A,B,C,D…。
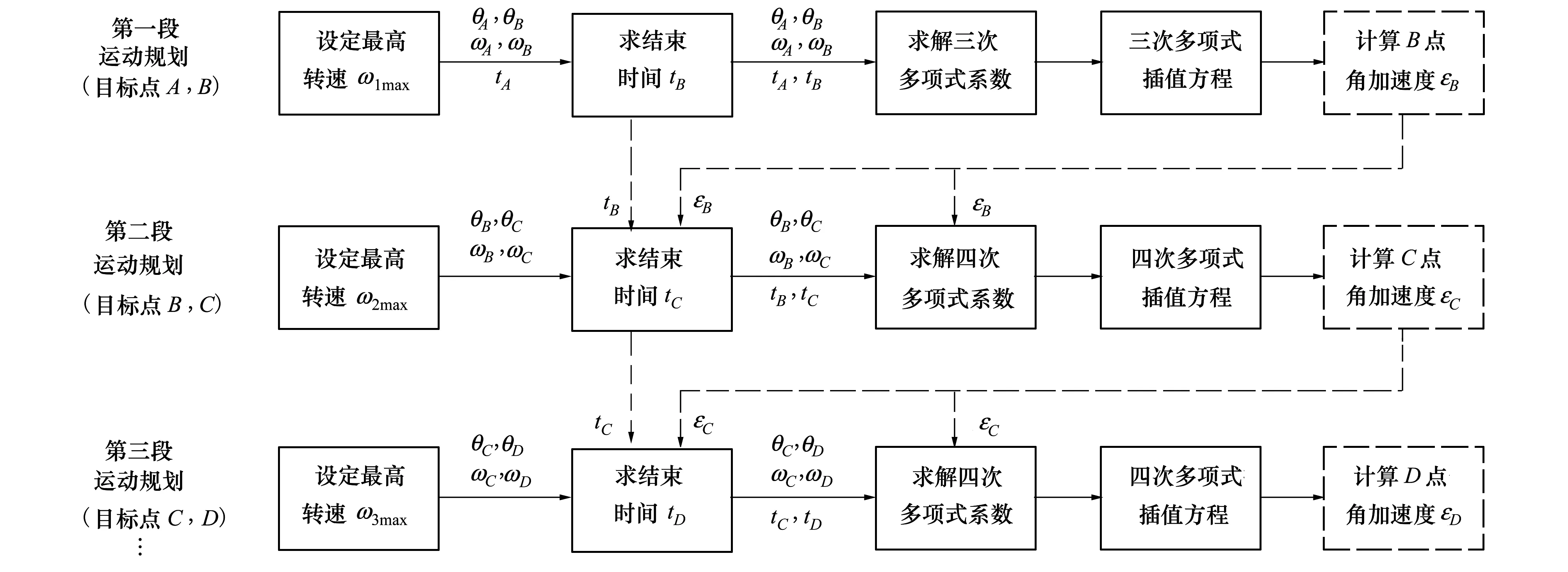
图6 3-4-…-4-4混合多项式运动规划流程图
1) 第一段运动规划采用三次多项式插值。根据目标点A和B的角位移和角速度约束条件θA,θB,ωA,ωB,初始时间tA(tA=0),并设定关节最高转速ω1max,求解运动结束时间tB。
2) 根据θA,θB,ωA,ωB,tA,tB,运用(6)式,求解三次多项式插值方程的系数,得到第一段运动规划方程。
3) 根据第一段运动规划方程,求得目标点B的角加速度εB,以供第二段运动规划使用。
4) 第二段运动规划采用四次多项式插值。根据目标点B和C的角位移和角速度约束条件θB,θC,ωB,ωC,初始时间tB,B点角加速度εB,并设定关节最高转速ω2max,求解结束时间tC。
5) 根据θB,θC,ωB,ωC,tB,tC,εB,运用(10)式,求解四次多项式插值方程的系数,得到第二段运动规划方程。因为第一段规划与第二段规划在连接点B处角加速度相等,所以确保这两段规划曲线在连接点B处角加速度是连续的。
6) 根据第二段运动规划方程,求得目标点C的角加速度εC,以供第三段运动规划使用。
7) 如果还有后续目标点,后面的运动规划都采用四次多项式插值,重复步骤4)~6),直到完成所有目标点的运动规划。
从上述原理与步骤中可以看出,这种规划方法不但能保证连接点处角加速度的连续性,且不用预先设定目标点处角加速度的值,避免不合理角加速度预定值带来的角速度波动。
4 算例验证与分析
为了证验本文提出方法的合理性和有效性,运用相关算例进行验证与分析说明。
算例工业机器人为了完成某项工作任务,关节1需要进行速度约束的点到点运动,从起始点A开始转动,依次经过B,C,D,E点,各目标点的转动量如表1所示。使用本文提出的三、四次多项式混合插值,对该关节进行速度约束的点到点运动规划。
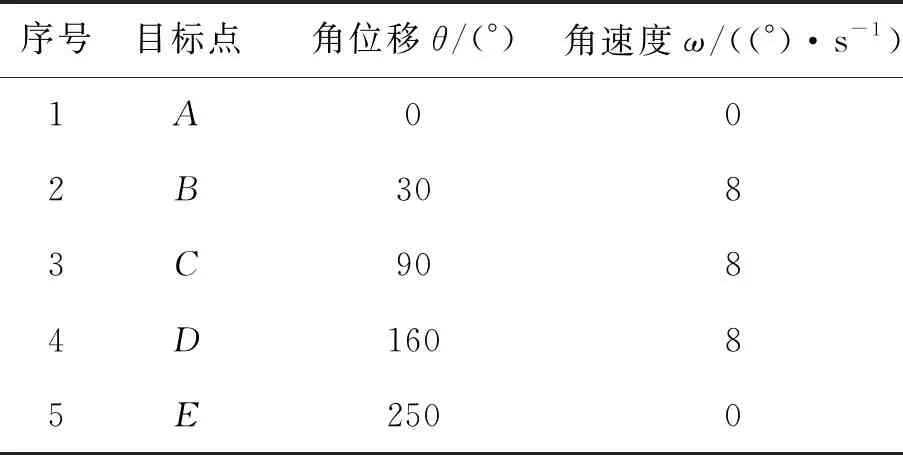
表1 关节1目标点约束条件
1) 第一段运动规划,三次多项式插值。从速度平稳性考虑,对于三次多项插值,取2个目标点较大速度为最大速度,ω1max=8,求得第一段运动结束时间为5.625 s,适当取整之后,取结束时间tB=5 s。
根据(6)式求解第一段运动规划三次多项式的系数,得到第一段运动规划方程,如(17)式所示。
θ1(t)=2t2-0.16t30≤t≤5
(17)
根据该方程,得到第一段规划结束点B的角加速度εB=-0.8°/s2以供第二段运动规划使用。
2) 第二段运动规划,四次多项式插值。从速度平稳性考虑,对于四次多项插值,最大速度设定为略高于2个目标点较大转速,ω2max=8.5°/s,并求解第二段运动结束时间tC,去除复数解及异常解,有2个合适解12.55和13.29,适当取整之后,取结束时间tC为13 s。
根据(10)式求解第二段运动规划四次多项式的系数,得到第二段运动规划方程,如(18)式所示。
5≤t≤13 (18)
根据该方程,得到第二段规划结束点C的角加速度εC=-0.05°/s2以供第三段运动规划使用。
3) 第三段运动规划,四次多项式插值。从速度平稳出发,取关节最大速度为ω3max=8.5°/s,并求解第三段运动结束时间tD,去除异常解,适当取整之后,取结束时间tD为22 s。
根据(10)式求解第三段运动规划四次多项式的系数,得到第三段运动规划方程,如(19)式所示。
13≤t≤22 (19)
根据该方程,求得第三段规划结束点D的角加速度εD=0.246°/s2以供第四段运动规划使用。
4) 第四段运动规划,四次多项式插值。从速度平稳出发,取关节最大速度为ω4max=8.5°/s,求解第四段运动结束时间tE,去除复数解和异常解,取整之后,取结束时间tE为35 s。
根据(10)式求解第四段运动规划四次多项式的系数,得到第四段运动规划方程,如(20)式所示。
22≤t≤35 (20)
至此,关节的运动规划完毕。验证运动规划的目标点是否满足边界约束条件,见表2。从表2中可以看出,4段运动规划的目标点都满足算例给定的角位移和角速度约束条件,并且在各段连接点处角加速度相等,保证了角加速度的连续性。

表2 目标点运动量检验
根据求得的4段运动规划方程,绘制如图7所示的运动规划曲线。如图7a)所示,角位移规划曲线变化平缓,并且目标点满足角位移的约束条件。如图7b)所示,目标点满足角速度约束条件,并且整个角速度曲线光滑平稳,波动较小,并且没有出现大的角速度峰值,说明所提出的运动时间计算方法是合理可行的。如图7c)所示,角加速度变化平稳,在各段连接点处是连续的,无间断点。算例验证了本文提出的运动时间计算方法的合理性以及所提出的3-4-…-4-4混合多项式规划方法的合理性和有效性。
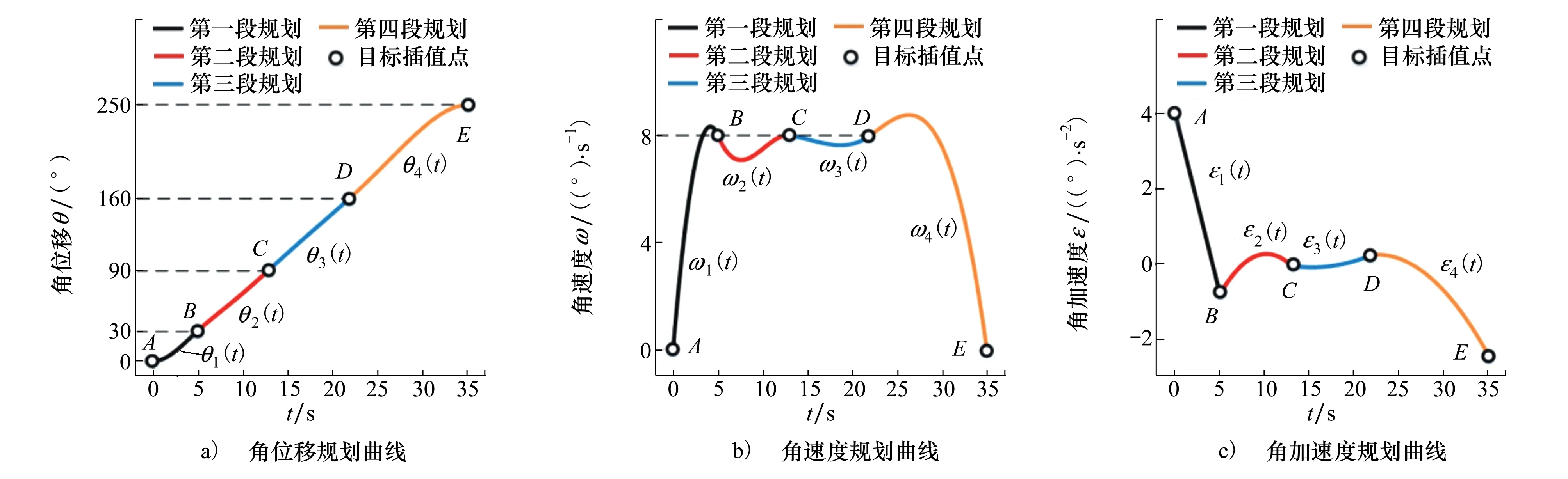
图7 3-4-4-4混合多项式运动规划
本算例又分别采用了三次多项式和3-5-5-3混合多项式进行规划,与本文提出的3-4-4-4多项式规划进行比较。图8是3种运动规划的角位移曲线,3种规划都能满足目标点角位移要求,角位移曲线基本相似,没有太大差别。

图8 3种运动规划的角位移曲线
图9是3种运动规划的角速度曲线。如图9b)所示,三次多项式规划的角速度曲线整体变化平稳,角速度波动不大,但是连接点处有明显的尖锐点,在C点尤为明显,说明在连接点处角加速度虽然连续但是并不平滑,如图9c)所示,3-5-5-3规划的角速度曲线在第二段和第三段中波动较大,说明在连接点C的角加速度预设定的值不适当,因此造成角速度曲线有较大的波动,角速度不平稳。如图9a)所示,采用本文提出的3-4-4-4规划方法,角速度曲线整体变化平稳,在连接点处角速度光滑平稳。

图9 3种运动规划的角速度曲线
图10是3种运动规划的角加速度曲线。如图10b)所示,三次多项式规划在连接点B,C,D处角加速度出现明显间断点,在连接点处角加速度不连续,将会产生振动和冲击,不利于工业机器人的工作性能和使用寿命。如图10c)所示,3-5-5-3规划方式的角加速度在连接点处是连续的,但是在五次多项式规划段中,角加速度波动较大。如图10a)所示,采用本文提出的3-4-4-4规划方法,角加速度在连接点是连续的,并且整个加速度曲线变化较平稳。

图10 3种运动规划的角加速度曲线
从上述比较分析中可以看出,本文提出的方法进行3-4-4-4混合多项式规划,相比于三次多项式和3-5-5-3多项式规划,能更好地应用于速度约束的点到点运动规划中,满足目标点角位移与角速度约束要求的同时,保证了运动规划角加速度的连续性,且不用预先设定目标点角加速度的值,减小角速度变化波动。
5 结 论
对于速度约束的点到点运动,三次多项规划连接点处角加速度不连续,出现间断点,会引起振动和冲击,不利于机器人的使用寿命和工作性能。五次多项式规划解决了角加速度不连续问题,但需要预先设定目标点处的角加速度,如果预先设定的角加速度值不合适则会引起角速度来回波动,不利于控制。对于现有的多项式样条曲线拼接方法,4-3-…-3-4多项式规划的角加速度虽然连续,但是不能指定中间目标点的角速度值,3-5-…-5-3多项式规划方法因为五次多项式的存在,也需要预先设定角加速度,同样容易引起角速度较大的波动。
针对这些存在问题,本文提出了3-4-…-4-4混合多项式插值规划,这种规划方法主要有以下几个优势:①在指定中间目标点角速度的同时,能够确保在连接点处的角加速度是连续的,不会出现角加速度间断点;②不需要预先设定目标点的角加速度,避免预先设定的加速度值不适当引起角速度波动;③提出运动时间的计算方法,避免运动规划中出现速度峰值过大的现象,并且使规划的角速度波动较小;④相关算例验证了所提方法的有效性和合理性,较好地解决了现有规划方法存在的问题,能够很好应用到速度约束的点到点运动规划中,有利工业机器人的工作性能和使用寿命。

