新型无铁芯永磁同步直线电机推力性能优化设计及试验*
李 博,张君安,李子昂,刘 波
(西安工业大学 机电工程学院,西安 710021)
近年来,随着“工业 4.0”与“智能制造2025”的提出,永磁同步直线电机在自动化生产领域得到了充分的利用,也成为了工业伺服领域研究的热点[1]。因此开展ACPMSLM推力提高及推力波动抑制的研究具有重要的理论和实践意义[2]。
无铁芯永磁同步直线电机(Air Core Permanent Magnet Synchronous Linear Motor,ACPMSLM)由于不使用铁芯,且无齿槽结构使得其拥有高定位精度、零定位力等优点,故广泛应用于超精密定位的直线驱动系统中[3]。电机定子结构通常采用径向磁体排布或Halbach阵列两种形式,其中 Halbach永磁阵列可以将一侧磁场加强,另一侧磁场减弱,提高了电机的推力密度[4]。
目前国内外多数团队从电机结构与控制策略两方面进行推力提高及推力波动削弱研究。文献[5]基于等效磁化电流法对无铁芯永磁同步直线电机的磁场模型进行了求解,并推导出了电机的推力公式,研制了样机并进行了试验测试。文献[6]详细分析了无铁芯盘状电机的结构特征,动子采取Halbach磁极布置,并对该种结构电机的优缺点,制作成本等也进行了评价。
文献[7]建立矩形无铁芯永磁同步直线电机的数学模型,并根据其模型推导出了电机的推力常数、反电动势常数等参数,比较了采用矩形磁极和Halbach磁极对电机性能的影响,研制了采用矩形磁极布置的样机,最后进行了简单的电气参数的测量。文献[8]针对无铁芯永磁同步直线电机的横向端部效应进行了研究,提出了横向漏磁系数的表征概念,对电机散热效果进行分析,并给出水冷却系统方案。文献[9]基于麦克斯韦应力张量法对无铁芯永磁同步直线电机建立数学模型,得出推力谐波是影响电机推力波动的主要因素,降低电机的推力波动可通过降低其推力谐波含量实现。
本文研制一种新型永磁体结构的无铁芯永磁同步直线电机并对其关键结构参数优化以解决推力及推力波动问题。提出新型永磁体结构设计原理,建立物理模型。对新型磁极结构的磁场进行有限元分析,通过有限元对新型磁极布置下电机的推力与推力波动进行仿真分析,以推力不削弱、推力波动最小作为优化目标,进行样机研制,通过重复定位精度的测量验证新型磁极阵列所设计的电机抑制推力波动的有效性。
1 新型ACPMSLM拓扑结构设计
Halbach磁极布置结构作为一种优化方案,对提高无铁芯直线电机的推力性能具有积极的作用[10]。Halbach磁极布置如图1所示,一侧磁力线因相互抵消而减弱,另外一侧因相互叠加而加强。

图1 Halbach磁极布置
1.1 多段式Halbach磁极布置推力性能比较
Halbach布置按其一个极距下充磁方向的角度变化可分为两段式Halbach、三段式Halbach、四段式Halbach等。通常段数越高,充磁方向越复杂。
两段式Halbach的物理模型如图2(a)所示,其充磁方向按90°依次变化,在一个极距内充磁方向改变两次。三段式Halbach的物理模型如图2(b)所示,其充磁方向按90°、45°交错变化,一个极距内充磁方向变化三次。四段式Halbach的物理模型如图2(c)所示,其充磁方向按45°变化,一个极距内充磁方向变化四次。

图2 多段式Halbach布置物理模型
在无铁芯永磁同步直线电机中,采用四段Halbach与常规磁极相比,其气隙中心线磁密幅值将会大幅提高,通过采用多段式Halbach磁极布置的结构,可以增强无铁芯永磁同步直线电机气隙中心线磁密的幅值和正弦性,从而增大无铁芯永磁同步直线电机的推力并减小其推力波动,这将有利于增强它的精密伺服性能。
1.2 新型Halbach磁极布置
采取四段式Halbach磁极布置对增强无铁芯永磁同步直线电机的伺服性能有非常积极的效果。但四段式Halbach磁极布置中包含的45°充磁方向的永磁体对充磁工艺要求较高,相邻永磁体之间的作用力给样机的组配也带来了不小难度,且一个极距内永磁体个数较多,耗费工时。为此可采取一种新型磁极布置,希望其产生的效果与四段式Halbach磁极布置相近,工艺上又相对较容易实现。
图2(c)中四段式Halbach磁极布置的物理模型,其45°充磁方向的永磁体从原理上可以由图3等效,其45°充磁方向可以视为横向与径向充磁方向的叠加。

图3 Halbach磁极布置45°充磁方向
根据图3叠加原理得到如图4所示的四段式Halbach布置物理模型。
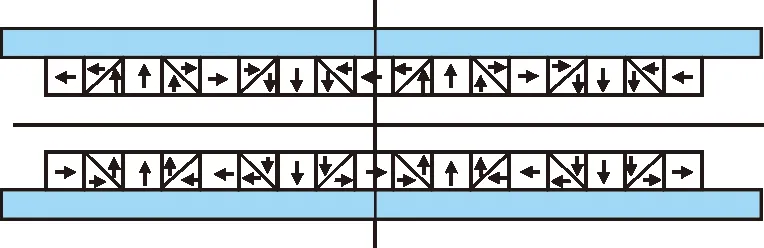
图4 四段式Halbach布置物理模型
由图4可观察到,原来彼此相邻的充磁方向不同的三块矩形永磁体可变为单块矩形永磁体与相邻两块三角形永磁体的叠加,且单块矩形永磁体的充磁方向与相邻三角形的充磁方向相同,于是由图4可等价转换为如图5所示的新型Halbach磁极布置结构。

图5 新型Halbach磁极布置结构物理模型
2 新型ACPMSLM磁场有限元分析
2.1 有限元磁场分析的数学模型及边界条件
在电磁场的求解区域中,若电机为稳态磁场,则不需要考虑位移电流,因此可得麦克斯韦微分方程组[11]:
(1)
式中:H为磁场强度;J为传导电流密度;D为电通量密度;E为电场强度;B为磁通密度;ρ为电荷密度;t为时间变量。
在无铁芯永磁同步直线电机中不同介质分界面上磁场满足边界条件[12-13],即
1) 磁感应强度法向分量连续,即
Bn1=Bn2。
(2)
2) 磁场强度切向分量连续,即
(3)
式中:Bn1与Bn2分别为磁通密度B1与磁通密度B2的法向分量;Ht1与Ht2分别为两侧磁场强度切向分量;μ1与μ2分别为边界两侧磁导率;A1与A2分别为边界两侧矢量磁位;n为单位矢量。
永磁体内部磁场为静态磁场,对外表现为泊松方程形式的矢量场。式(3)求解的边界条件为
(4)
式中:Ω为无铁芯永磁同步直线电机内部静态磁场区域;μ为磁导率;S为外部的边界;Az为S边界上的矢量磁位;L1为无铁芯永磁同步直线电机内部介质之间的交界线(除永磁材料外与气隙的交界线);L2为永磁材料与气隙的交界线;Jm为交界处的电流密度;x,y为边界位置坐标。
计算空间进行网格划分时要同时考虑计算机资源与求解精度,在满足求解精度的基础上节省计算时间[14-15]。经过网格划分后结果如图6所示,在气隙处与材料边界处三角形网格较密集,而较远处三角形网格分布较稀疏。无铁芯永磁同步直线电机的2D模型在求解区域的边界处与需要精确结果的气隙区域均进行了网格的加密处理。

图6 网格划分情况
2.2 Halbach磁极布置磁场分析
对两段式、三段式、四段式Halbach磁极布置结构的电磁场进行有限元计算。提取出各段式Halbach磁极布置在气隙中心线位置处数个极距下的磁感应强度,观察其幅值随距离变化的情况,如图7所示。
由图7可得,采用四段Halbach布置结构与常规磁极布置相比,其气隙中心磁感应强度幅值提高。为了比较该新型磁极布置与常规磁极布置、四段Halbach磁极布置的气隙中心磁感应强度,对新磁极布置方式进行有限元计算,结果如图8~9所示。
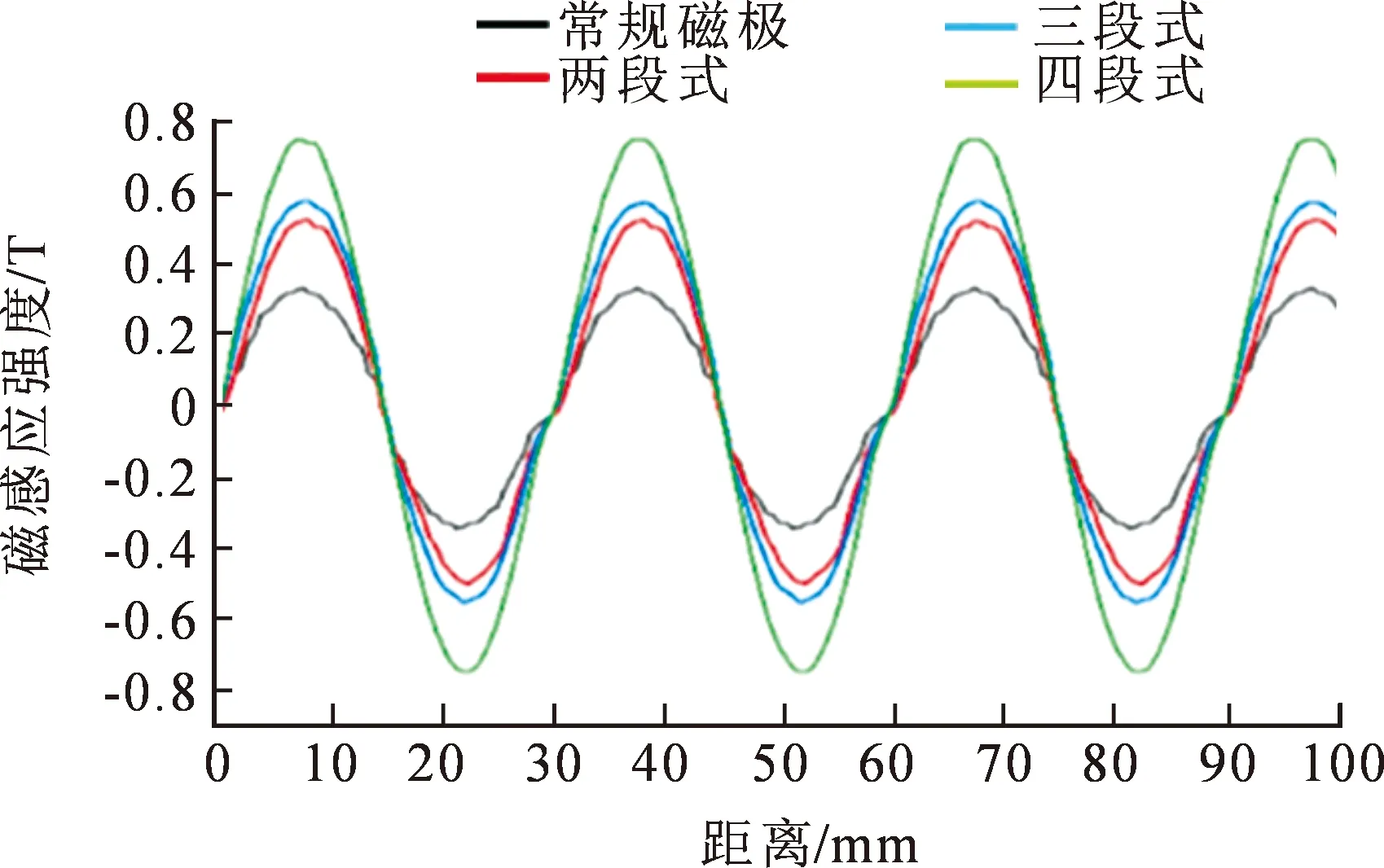
图7 气隙中心磁感应强度

图8 新型磁极布置磁场分布云图

图9 新型磁极布置磁力线分布图
在梯形布置高度已知的情况下(与常规径向布置相同),为进一步确定梯形永磁体模型上底a与下底b的最优值。已知a+b=τ,τ为极距,所以a,b取不同值,实际就是改变θ的大小,θ为梯形底边夹角。在此定义气隙磁场总谐波畸变率(Total Harmonics Distortion,THD)作为衡量波形正弦性的参数标准,其值为各谐波含量总和与基波含量之比[16]。θ改变时气隙中心磁感应强度幅值与气隙磁场总谐波畸变率变化情况见表1。

表1 对气隙中心磁感应强度幅值与气隙磁场总谐波畸变率的影响
由表1可知,当θ=65.8°时,无铁芯永磁同步直线电机所得的气隙中心磁感应强度幅值最大,气隙磁场总谐波畸变率最小。采用此新型磁极布置比常规磁极布置的气隙磁感应强度幅值提高了约2倍,其大小与正弦性接近于四段式Halbach布置。新型磁极布置减小了四段式Halbach布置工艺的复杂性。
分别建立采用常规磁极布置与新型磁极布置结构的2D仿真模型,动子采用四极三圈结构,对采用常规磁极布置与新型磁极布置进行了推力仿真计算,得到两种布置方式下的推力,如图10所示。
由图10可知,两种磁极布置方式通以相同大小的三相交流电时,电机采用新型磁极布置方式时的推力较采用常规磁极布置时增加,推力波动减小。这对提高无铁芯永磁同步直线电机的推力性能具有积极的影响。

图10 无铁芯永磁同步直线电机推力波形
3 重复定位精度测试
假设电机工作过程中,电机做往复匀速运动。理想状态下电机到达B1理想工作位置,实际工作中电机不会到达理想工作位置,而处在实际工作位置B2,B1与B2之间的距离Δx即可视为其重复定位精度。若测量出Δx的大小,可得电机的重复定位精度。
电机直线移动距离分别为20 mm、50 mm、100 mm时测量20次重复定位精度,如图11所示。
为检测两种磁极结构下无铁芯永磁同步直线电机重复定位精度的稳定性,利用变异系数(又称为标准离散差)进行分析,其值越高,表示数据的离散程度越大,其计算公式为
CV=(SD÷MN)×100%。
(5)
式中:CV为变异系数;SD为数据的标准偏差;MN为数据的平均值。
经过计算得出常规磁极布置的三组变异系数依次为0.098 2,0.098 5,0.103 0,新型磁极布置的三组变异系数依次为0.078 8,0.092 5,0.099 5,可见新型磁极布置的变异系数均小于常规磁极布置的变异系数。并随着直线定位行程的增加,重复定位精度的降低将导致变异系数的增大,符合实际情况。
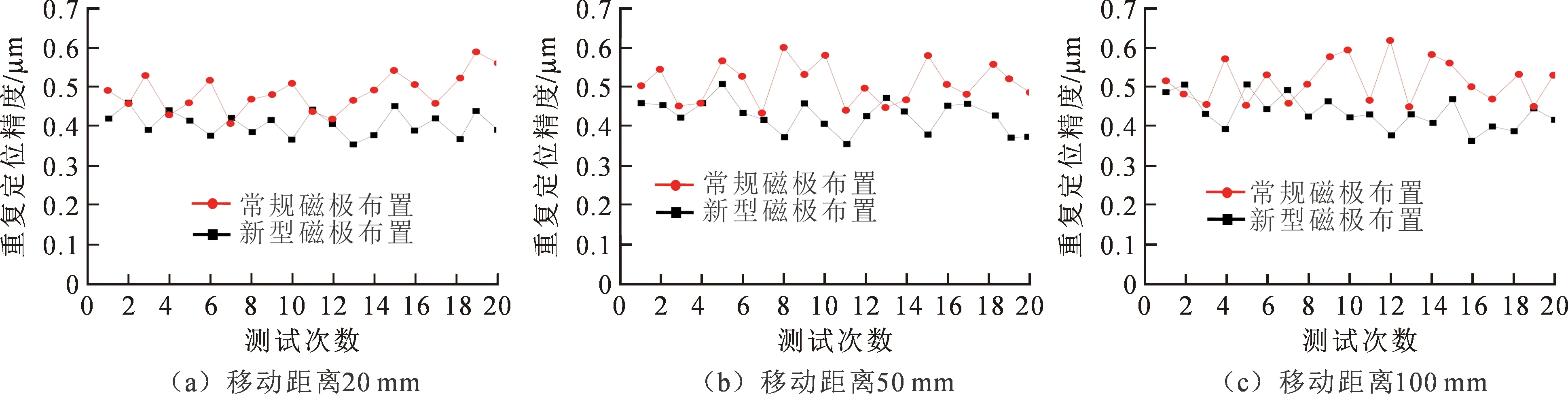
图11 重复定位精度测试
4 结 论
1) 文中所提出的新型磁极布置在效果上可以替代四段式Halhach磁极布置,从工艺上比四段式Halbach磁极布置更易实现。
2) 文中所提出的新型磁极布置与常规磁极布置相比,提高了无铁芯永磁同步直线电机的推力,并降低了其推力波动率。
3) 实验表明,新型磁极布置的变异系数小于常规磁极布置的变异系数,采用此种新型磁极布置可以提高无铁芯永磁同步直线电机的定位精度。

