考虑电压暂降波形多样性的暂降特征评估

江友华，谢振刚，曹以龙

（上海电力大学电子与信息工程学院，上海 201306）

0 引言

随着高新技术产业的发展，企业自动化和信息化程度越来越高，电压敏感负荷的比例也越来越高，供配电系统接地故障和大功率设备启动造成的电压暂降问题备受关注。

据统计，由电压暂降引起的用户投诉占整个电能质量问题投诉数量的80%以上，电压暂降已成为最频繁、最严重的电能质量问题[1-2]。如何准确地对电压暂降特征量进行快速界定成为亟待解决的问题。文献[3-4]在进行电压暂降评估时将短路故障暂降波形视为矩形波，忽略了用户终端动态负荷特性。但电力系统中出现相当数量的感应电动机时，暂降波形将不再是常见的矩形，而是呈现多样性。为此，相关研究根据暂降波形特征对非矩形电压暂降指标进行修正[5-10]。文献[5]新定义了电压暂降持续时间概念，将电压暂降波形恢复阶段的剖面近似为K阶根式，并根据设备的耐受特性曲线的Umin修正了持续时间的定义。但此方法只适用于对电机启动的电压暂降波形分析评估。文献[6]将其等效为一系列暂降幅值下对应持续时间的矩形暂降，在求暂降严重度时采取逐一计算严重度取最大值的方式。仅对单相暂降分析，未考虑不平衡暂降的情形，且较单一幅值与持续时间的描述方式计算复杂。文献[7]通过对事件持续段电压幅值进行积分，可有效表征整体幅值水平，而不仅仅依赖最低幅值评估暂降幅值的严重程度。但该方法只对事件持续段的电压进行积分，而非矩形暂降的过渡段较长且难以界定，尤其当故障时间较长时事件持续段较短，积分所得电压幅值结果失准。由此可知，虽然现有文献对非矩形特征值的界定做了相关研究，并取得一定成果，但对暂降幅值和持续时间描述并不完全准确，且存在计算复杂等问题，使相关暂降特征值的准确计算及后续评估工作难以开展。

针对电网中电压暂降的波形多样性、复杂性及上述电压暂降特征值分析评估的不足，文中应用恒暂降能量的思想提出了等效矩形暂降的方法，使原来的不平衡或非矩形暂降和转化后的矩形暂降具有相同的电压暂降能量损失。可以更准确地界定暂降特征值，旨在更好的展开电网中电压暂降相关研究的后续评估。

1 电压暂降波形的典型分析及描述方法

1.1 电压暂降波形的典型分析

电压暂降产生的本质原因[11]为系统中突然出现大电流，在导致系统阻抗上的分压增大，造成PCC点电压突然降低。系统内突然的大电流原因有很多，系统侧原因有短路故障、大型变压器空载激磁等，用户侧原因有大容量感应电动机启动、大负荷投切等。考虑到电压暂降在网络中传播以及动态负荷对故障清除后电压暂降恢复的影响，徐永海等将264次有效电压暂降事件作为研究样本，按不同电压等级将常见电压暂降监测波形统计见表1。图1中给出了相应暂降类型的电压暂降均方根值波形。

表1 不同电压等级下典型波形对应的电压暂降概率Table 1 Voltage sag probability corresponding to typical waveform under different voltages %

图1 电压暂降典型均方根值波形Fig.1 Typical RMS waveform of voltage sag

表1中，电压暂降波形按照波形的形态主要分为3种类型。第1类暂降是矩形波，主要是由短路故障引起，占比68.56%。其均方根值波形如图1（a）所示，电压暂降开始和恢复阶段波形陡，基波电压的幅值变化过程呈矩形，并且不同故障类型引发的电压暂降具有不同特征。第2类暂降属于左快右慢型，主要由电机启动不当或变压器励磁涌流造成，占比20.44%。其均方根值波形如图1（b）所示，电压暂降开始时，电压幅值突然下降，并逐渐恢复至正常值，三相暂降幅值相同，且持续时间较长。

第3类左慢右快型暂降是基于文献[12]静态计算和瞬态仿真讨论了受感应电动机负荷影响的线路故障在电机侧所引起的非矩形暂降波形，其有不同的表现形式：其中图1（c）为电压尚未下降至稳定值而故障已被清除，电压开始恢复，故暂降波形呈现三角状，图1（d）对应故障切除时电压已经下降至稳定值的情况。其较第1类暂降整体幅值更高，持续时间更长，且该类暂降具有时变幅值特性。电压的变化率为在一定时间内，电压幅值下降或恢复的多少。以图1（c）为例，最低幅值附近10 ms内，电压下降阶段，电压变化率为0.04 p.u./ms，电压恢复阶段，电压变化率为0.053 p.u./ms，故本文将其归为第3类左慢右快型暂降。虽然此类暂降类型的占比较少，但其影响不可忽略。还有其他类暂降如雷击造成的绝缘子闪络等不规则暂降波形。

1.2 电压暂降表征方法

国标GB/T 30137—2013中[13]，取暂降过程中电压方均根值的最小值占标称电压比值为暂降幅值，低于阈值电压（取典型值0.9 p.u.）的时间为持续时间。通过相数组合及时间组合进行不平衡暂降和多暂降事件的统计。相数组合结果为最低暂降幅值的均方根值，时间组合法将1 min内的连续数次暂降归并为一次暂降，持续时间累计[14]。

电压暂降特征表征方法见图2，图2（a）将矩形暂降波形分为暂降事件持续段和过渡段，可根据最低幅值和对应的持续时间来度量暂降幅值和持续时间维度严重程度。图2（b）将非矩形暂降波形分为持续暂降阶段以及故障后的电压恢复阶段。文献[7]中非矩形评估用数学表达式描述故障恢复阶段，忽略了持续暂降阶段的影响，故仅适用于第2类电压暂降波形的特征值计算。对于矩形暂降过渡段边界的界定容易，而非矩形暂降电压幅值具有时变特性，采用文献[9]评估方法刻画电压暂降幅值和持续时间不再适用于类似图2（b）的非矩形暂降。因此需要更全面、更合理的方法对电压暂降特征量进行界定。

图2 电压暂降特征表征方法Fig.2 Voltage sag characteristic characterization method

2 电压暂降波形的特征评估

电压暂降特征量的界定是电压暂降分析和评估中的首要工作。如1.2小节所述，由于电压暂降波形存在非矩形现象，且现有电压暂降特征值的计算具有不准确性及计算复杂性。为此，对于电压暂降相关的研究，有必要对暂降特征的描述方法进行修正。

能量指标同时兼顾了持续时间和暂降幅值两个暂降特征值，且考虑了暂降波形信息，具有合理性[15-16]。电压暂降能量Evs是指暂降事件损失的能量，伴随着暂降的发生会导致负载相应的能量损失。

文献[17]论述了暂降能量计算方法包括全过程法，半周波法和采样点法。全过程法适用于矩形电压暂降，半周波法的测量数据窗口为半周波的电压方均根测量值，每半个周波更新一次，一般用于实际监测。由于暂降波形存在多样性，文中选用采样点法计算负荷侧的能量损失指标。根据原来的不平衡或非矩形暂降和转化后的矩形暂降具有相同的电压暂降能量损失的方法，将非矩形暂降转换为等效矩形电压暂降，以便于电压暂降的特征提取。

IEEE Std.1564—2014标准[18]中给出的电压暂降能量指标定义中，隐含地给出了暂降幅值和持续时间之间的转换关系。阈值电压取典型值0.9 p.u.，Evs的计算如式（1）所示。

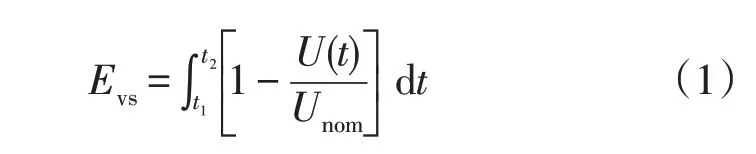
由于第1类暂降的电压均方根值在暂降期间是基本恒定的，且持续时间易获取。三相平衡矩形暂降可用全过程法计算暂降的能量损失，如式（2）所示。

对于不平衡矩形暂降，非故障相电压幅值一般高于0.9 p.u.，其电压暂降影响较小，一般忽略不计。由于故障相的电压幅值不一，需将出故障相的电压幅值归一化。分别计算各相暂降能量并求和，如式（4）所示，根据文献[19]提出的相数组合方法计算出三相暂降的持续时间Tsag。

进而结合式（2）计算出电压暂降幅值归一化指标，如式（5）所示。

而对于第2、3类的非矩形暂降的电压幅值具有时变性和电压恢复阶段缓慢的特征，使用Umin和Tsag两个参数计算不能准确表征幅值和持续时间两个暂降特征，从而得不到准确的暂降能量损失指标。本文对电压幅值低于0.9 p.u.的波形进行积分运算来反映整体电压水平，如式（6）所示。

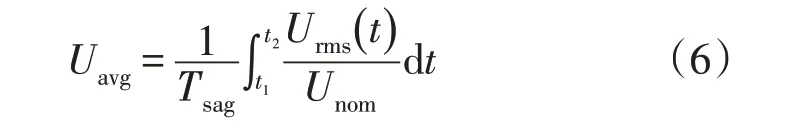
式中：Urms(t)为电压均方根值的标幺值；t1、t2为暂降发生的起止时间；Unom为标称电压。

采用统一的采样频率和方法，对波形进行数字化处理，用一组坐标点定义暂降曲线[(U1，t1)，(U2，t2)，...，(UN，tN)]，将式（2）和式（6）离散化，得到非矩形单相电压暂降幅值期望值与能量损失指标，表达式如式（7）、式（8）所示。

式中：ΔT为相邻采样点的时间间隔；Urms(k)为暂降期间各采样点电压有效值的标幺值；N为Urms(k)低于0.9 p.u.的采样点数；Urms(k)为事件过程中第k个采样点的电压均方根值。

最后结合式（2）和式（7）-（8）求得单相电压暂降持续时间的新定义，如式（10）所示，将不平衡非矩形暂降等效为不平衡矩形暂降。

最后，根据不平衡矩形暂降处理方法，将三相电压暂降幅值进行归一化，结合式（2）、式（4）和式（10）可计算幅值归一化指标。公式为

3 仿真模型

利用PSCAD/EMTDC仿真工具对拓扑如图3所示的系统进行电压暂降仿真分析。用户由2个220 kV变电站和2个110 kV变电站中的5条10 kV线路供电，用户线路均为YJV-300的电缆。系统将500 kV母线和110 kV电厂作为恒压源供电，考察架空线路发生短路故障造成的用户电压暂降情况。

图3 系统仿真拓扑图Fig.3 Simulation topological diagram of system

文中将节点1-5作为用户评估节点，采用感应电动机并联恒阻抗负荷来模拟节点4、5的综合负荷特性，其他节点负荷采用等值恒阻抗模型[20]模拟。不同电压等级输电线路参数通常采用典型值[21]，感应电机参数见表2。

表2 感应电动机主要参数Table 2 Main parameters of induction motor

4 仿真结果分析与验证

本节使用第3节的电力系统模型仿真得到的低于0.9 p.u.电压阈值的电压均方根值采样数据和对应的持续时间数据。将其导入Matlab故障分析程序，计算出各节点的暂降能量指标，并由第2节介绍的暂降能量等效算法提取出各节点电压暂降的特征值。

以L2发生A单相短路接地故障引起的电压暂降为例，Timed Fault Logic模块设置故障发生时间为0.3 s，故障持续时间为60 ms，仿真时长设置为0.5 s，采样频率取10 kHz。采样时间从0.25 s开始直到仿真结束，则采样点数为2 501，和实际电能质量监测所取采样点数相同。考察感应电动机的动态响应对短路故障的暂降特征值的影响，对负荷节点1-5处的暂降情况进行仿真分析。

负荷节点处电压均方根值波形见图4。其中，图4（a）为节点1-3暂降波形，属于第1类暂降，暂降最低幅值为0.51 p.u.，持续时间为70.9 ms；图4（b）可以看到节点4-5的暂降波形，属于第3类暂降，暂降最低幅值为0.58 p.u.，持续时间为75.7 ms。对比暂降幅值和持续时间发现考虑感应电动机的综合负荷模型使暂降波形变浅且变长，使得电压包络曲线不同，验证了1.1节中分析的正确性。

图4 负荷节点处电压均方根值波形Fig.4 Voltage RMS waveform at load node

以故障前节点的标称电压为基准值，得到的仿真结果均以标幺值表示。根据式（8）计算出负荷节点1-5出现的电压暂降能量对比见图5。

图5 各节点电压暂降能量指标值Fig.5 Voltage sag energy index of each node

由图中可知，节点电压暂降能量损失指标存在差异性，这可以解释为感应电动机的动态响应为网络提供了无功支持，以防止电压快速崩溃[22]。

根据最低幅值和低于阈值电压的持续时间的传统方法和文中方法计算得到电压暂降特征，为了更直观地表示出两种计算方法的差异性，作图6可以得到直观清晰的电压暂降特征值比对结果，并将计算结果列于表3中进行特征比对。

表3 考虑感应电机的电压暂降特征值对比Table 3 Comparison of voltage sag characteristic value considering induction motor

图6 电压暂降特征值对比Fig.6 Comparison of voltage sag characteristic values

由节点1-3暂降特征值分析结果可知，如果电压暂降波形是矩形，则有，用采样点法和全过程计算出的暂降特征结果接近，这意味着文中方法完全适用于矩形暂降。由节点4-5的对比结果可知，采用文中方法的电压暂降特征计算结果较传统方法计算得出的暂降幅值更高，持续时间更短。这是感应电机有抗拒电压突变的作用[12，22-23]，对故障清除后电压暂降恢复有影响，使得非矩形暂降波形在短时间内不会跌落至最低值，并且电压恢复阶段缓慢。

文中方法考虑了整体电压水平以及暂降的能量损失，更能体现电压暂降波形的整体特征，可以有效减小因忽略感应电机负荷对评估结果造成的影响。对于单相短路故障，不管暂降波形是否为矩形波都能有效评估电压暂降的特征值，使电压暂降的评估更具准确性和可信度。

为了进一步验证文中特征评估方法的有效性，文中同时采用传统方法和文献[6]多暂降阈值的方法作为对照。在节点5处先模拟感应电机定子回路串联1Ω电阻启动，然后模拟短路故障各种类型，全面考察节点5的电压暂降特征，将暂降特征值的计算方式分为3种，进行对比分析，见表4，验证恒能量理论的有效性及可行性。

表4 电压暂降特征值的计算方式Table 4 Calculation mode of voltage sag characteristic value

为方便比对，将上述3种计算方式计算得到的特征值进行汇总，见表5，方式1的传统计算方法只采用最低幅值，造成电压幅值的过度评估，对电压恢复阶段缓慢的暂降也会造成持续时间的过评估。方式2的多暂降阈值将暂降波形等效为一系列矩形暂降，计算结果较方式1更准确，但其较单一幅值与持续时间的方式计算量大。方式3的计算结果与方式2具有相同的准确度，计算多个电压暂降的波形的特征量时，较方式2能够更简单快速，为后续暂降评估工作提供便利。

表5 节点5各种暂降特征分析Table 5 Analysis of various transient characteristics of node 5

5 结语

电压暂降源存在复杂性、多样性、随机性等特点，采用现有电压暂降特征值计算会导致暂降特征计算存在不准确和计算复杂的问题，进而造成电压暂降相关评估结果的失准。

文中综合分析了各种类型的电压暂降，并给出了各自波形，在电压暂降表征的基础上引入恒暂降能量理论，提出了一种将不平衡和非矩形暂降等效为矩形三相平衡暂降的方法，给出了暂降特征值的数学表达式和电压暂降评估模型。文中仿真模型考虑了感应电动机对电压暂降特性和传播的影响，不管暂降波形是否平衡或矩形都能有效评估电压暂降的特征值，使电压暂降的评估更具准确性和可信度。