偏度约束下单位收益风险最小的投资组合模型构建与实证
刘洪民(总会计师)战颖(高级会计师)乔运锋(高级会计师)
(1,2中冶北方工程技术有限公司 辽宁大连 114051 3中冶焦耐工程技术有限公司 辽宁大连 114031)
一、引言
投资组合问题是现代财务学研究的起源,诺贝尔经济学奖获得者Markowitz使用方差度量风险并构建均值-方差模型来定量研究资产的优化配置,标志着现代投资组合理论的诞生。由于方差将收益率向上的有利波动也视为风险,显然是夸大了风险,与实际不符。对此,学术界提出了其他投资组合模型。
以风险或收益是否给定为标准,可将现有的投资组合模型分为两大类。
第一类是既定风险下收益最大化或者既定收益下风险最小化的投资组合模型。其中,比较有代表性的是VaR模型,VaR(Value at Risk)主要用于衡量某一资产组合在市场正常波动时所遭受的潜在损失,它是三十国集团于1993年正式提出的,被巴塞尔银行监管委员会于1995年所采纳并加以推广应用。但Artzner(1997)证明了VaR不满足风险测度一致性公理中的次可加性,是一种不够完善的风险度量方法。针对 VaR 的不足,Stanislav(2000)提出 CVaR(Conditional VaR),它是指某一资产组合的损失超过VaR的条件均值,反映了超额损失的平均水平。Stanislav证明了CVaR满足次可加性,比方差和VaR更能有效地测度投资组合风险。李锋刚等(2016)通过实证检验发现我国股票收益率不服从正态分布,采用改进粒子群算法来求解非正态分布下的均值-CVaR模型。
第二类是基于单位风险收益最大化或者单位收益风险最小化的投资组合模型,主要研究如何对投资组合的收益与风险进行综合权衡。其中,武敏婷等(2010)采用均值与VaR的比值测度单位风险收益,并构建了单位风险收益最大化的投资组合优化模型。高培旺(2011)使用标准差与均值的比值即变异系数来度量单位收益风险,并建立了基于变异系数最小的投资组合模型。由于VaR、标准差(即方差的平方根)均不是完善的风险度量方法,吴雷等(2013)选用CVaR与期望收益率之比来度量投资者为获得每一个单位收益所承担的风险,构建了单位收益风险最小化的投资组合模型。
上述模型大多关注收益的前两阶矩(即均值和方差),往往忽视了收益的三阶矩(即偏度)风险。早在1970年,著名经济学家Sanuelson就明确提出:如果资产收益率不服从正态分布,那么高阶矩风险特别是三阶矩风险就不容忽视。迟国泰等(2009)在均值-方差模型基础上引入偏度不小于零的约束,并证实偏度的引入可以降低投资组合风险。吴雷等(2014)在均值-CVaR模型的基础上引入偏度约束,构建了均值与偏度约束下CVaR最小的投资组合模型并予以实证。蔡小龙等(2017)通过引入偏度约束,构建了均值-方差-偏度-正弦熵的投资组合模型,实证结果表明偏度约束在控制风险的同时可实现更高收益。
上述第一类模型需要投资者事先设定收益率或风险,存在着较大的主观性和随意性,如果投资者将收益率设定得过高或过低,都可能导致投资者为获得每一个单位的收益而承担了过高的风险。而第二类模型没有考虑收益的三阶矩(即偏度)风险。综合考虑上述因素后,本文选用CVaR与期望收益率之比来度量单位收益风险,通过引入偏度大于等于零的约束条件来控制重大投资损失发生的概率,构建了偏度约束下单位收益风险最小的投资组合模型,并对模型作实证检验。
二、模型构建
(一)单位收益风险最小原理
现有文献通常采用期望收益率来度量投资组合的收益,使用方差、VaR、CVaR等度量投资组合的风险。如前文所述,方差高估了风险,VaR不满足次可加性,两者均不是完善的风险测度方法。现有研究已证实CVaR满足次可加性、具有凸性等特性,被认为是一种较为完善的风险度量方法。因此,本文选用CVaR测度投资组合风险。
CVaR是Conditional Value at Risk的缩写,通常译为“条件在险价值”,是指在一定期间和置信水平下损失超过VaR的条件均值。现有的CVaR模型大多是给定收益率使风险值CVaR最小,投资者要求的收益率越高,承担的风险值CVaR也越高。然而,这类模型忽视了另一部分投资者的需求:对收益率没有特定的要求,但希望为赚取每一元钱所承担的风险最小。此外,由于这类模型中的收益率是投资者人为设定的,存在着较大的主观性和随意性,如果投资者将收益率设定得过高或过低,都可能导致投资者为获得每一个单位的收益而承担了过高的风险。
表1列示的是三种不同类型的投资组合,其中,“甲”的期望收益率与风险值CVaR均较低,投资者过于“谨慎”,但单位收益风险(CVaR与期望收益率的比值)较高,也就是说,投资者设定了过低的收益率,可能导致其为获得每单位的收益而承担了较高的风险。相反,“丙”的期望收益率与风险值CVaR均较高,投资者较为“冒险”,但单位收益风险偏高,换言之,投资者设定了过高的收益率,可能导致了其为获得每单位的收益而承担了较高的风险。“乙”的期望收益率和风险值CVaR较为适中,但单位收益风险相对较低。很显然,理性投资者应选择“乙”,即选择单位收益风险最小的投资组合。

表1 不同期望收益率下的投资组合
本文选择CVaR与期望收益率的比值度量单位收益风险,并构建基于单位收益风险最小化的投资组合模型,该模型不需要事先给定收益率就能求解,既满足了部分投资者对收益率没有特定要求但期望赚取每一元钱所承担风险最小的需求,又对投资组合的收益与风险加以综合考虑,可以避免投资者对收益率设定过高或过低所导致的单位收益风险过高,减少了投资者事先对收益率的盲目估计行为,提高了投资的效率和合理性。
(二)模型构建的思路
本文以CVaR与期望收益率的比值来测度单位收益风险,通过引入投资组合收益率的偏度大于等于0约束来降低投资损失发生的概率,构建了基于偏度约束下的单位风险最小的投资组合优化模型,模型构建的具体思路如图1所示。

图1 偏度约束下单位收益风险最小的投资组合优化模型构建思路
(三)目标函数的建立
1.目标函数的表达式。由上文分析可知,以CVaR与期望收益率的比值来度量单位收益风险,可以有效避免投资者对收益率设定过高或过低所导致的单位收益风险偏高。因此,目标函数就是最小化CVaR与期望收益率的比值,即:

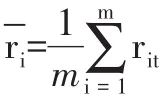
2.CVaR的表达式。根据CVaR的定义,可以得到:
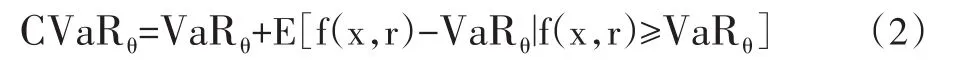
其中,发f(x,r)表示投资组合的损失函数,θ表示置信度。
通过式(2),无法直接求出CVaR,因为该式中含有内生参数VaR。本文参考Krokhmal(2002)设计的方法,对CVaR的计算进行离散化处理,得到CVaR的近似表达式:

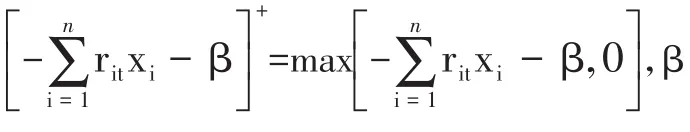
通过式(3)计算出的β值就是VaR,由此可见,在求解CVaR的同时顺便得到VaR。
3.目标函数的等价形式。综合式(1)和式(3),模型的目标函数可转化为:
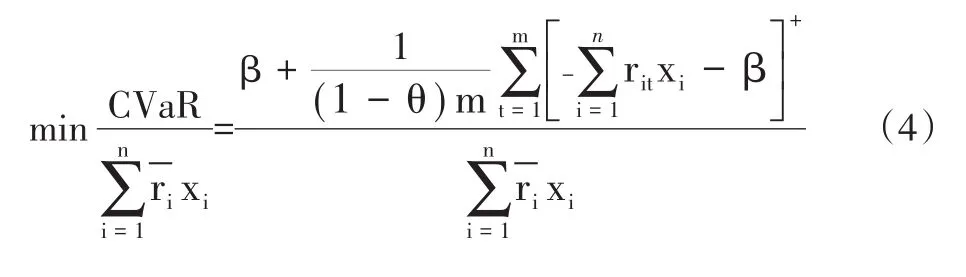
(四)约束条件的建立
1.偏度约束。偏度可用于衡量收益率概率分布的偏斜方向以及偏斜程度,其计算公式为:

其中:n为资产数量,r为第i项资产收益率,r为期望收益率,σ为收益率的标准差。
如图2所示,虚曲线M和实曲线N刻画的是期望收益率相同但偏度不同的两个概率分布,其中,M的偏度小于零,左尾长而右尾短,发生重大投资损失的风险较高;N的偏度大于零,左尾短而右尾长,发生重大投资损失的概率较低。显然,选择N进行投资,则在相同期望收益下,面临的风险更小,与投资者的期望相符。

图2 两个不同偏度的收益率分布
以偏度大于等于零作为约束条件,可以减少重大投资损失发生的几率,同时保留高收益发生的概率,进而降低投资风险,这正是使用偏度约束进行风险控制的基本原理。因此,本文引入了投资组合收益率的偏度为非负的约束,即:

2.投资比例约束。投资组合中所有资产的投资比例之和应等于1,即:

投资组合中每一项资产的投资比例通常不小于0,即:

(五)模型的建立
综合式(4)—(7),可以建立偏度约束下单位收益风险最小的投资组合优化模型,即:

其中:x表示投资比例,是模型最终所要求出的变量。
式(9)得到的模型与式(8)中的模型有相同的最优解,式(9)为一般的数学规划模型,可通过现有的数学软件就能求出最优解。
由此可见,对模型进行离散化和线性化处理后,不需要假定收益率是否服从正态分布就能求解,既降低了模型的求解难度,又提高了模型的实用性。同时,在求解CVaR的同时顺便得到VaR,而VaR在风险管理实践中使用较为普遍,模型的实用价值得到进一步提升。
三、实证研究
(一)数据收集与统计分析
本文从我国沪深股市抽取10只不同行业的股票进行投资,时间跨度为2020年1月1日至2020年6月30日,以每周三的股票收盘价为基础,采用对数方法计算股票周收益率r,其公式如下:

其中,P和P分别表示第i只股票在第t周和第t-1周周三的收盘价。
通过计算,得到了每只股票25个周收益率数据,有关描述性统计结果如表2所示。

表2 10只股票收益率的描述性统计
由表2可知,10只股票收益率的偏度和峰度均不为0,意味着这10只股票收益率均不服从正态分布,并且有8只股票收益率的偏度小于0,其收益率概率分布的“左尾”较长,出现低收益率的概率较大,投资风险也较高。其中,航天科技(股票代码000901)周收益率的偏度为-2.14,峰度高达6.09,其分布明显带有“尖峰厚尾”,且“左尾”较长,出现低收益率的概率较高。
(二)模型求解与分析
将m=25,n=10等数据代入式(9)中,置信度θ分别取90%、95%、99%,利用数学软件MATLAB进行求解,求解结果如表3所示。
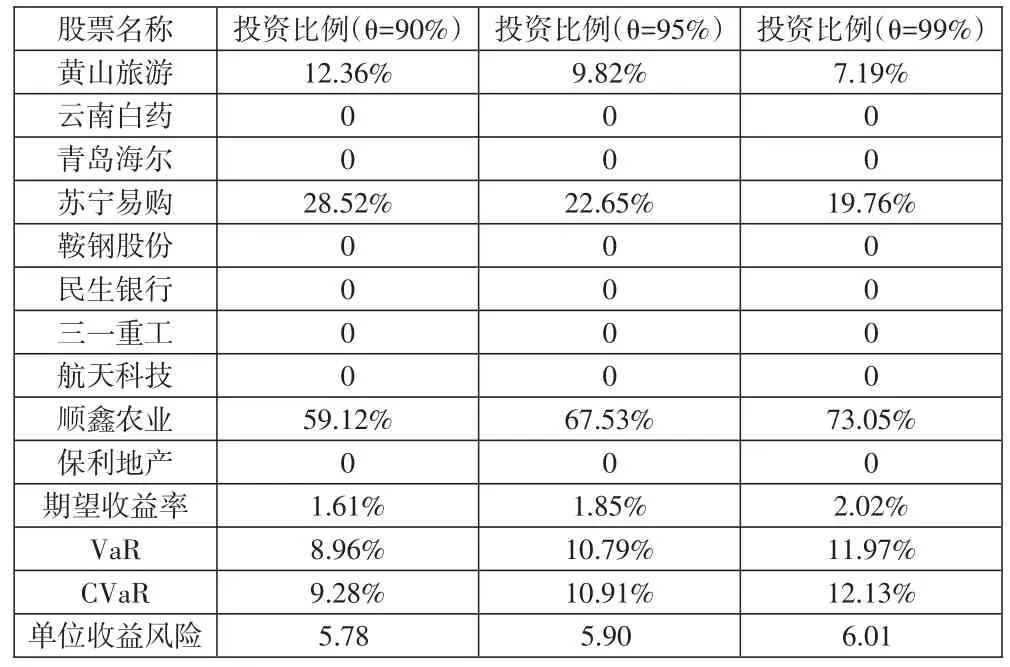
表3 模型求解结果
从表3可以看出,在三种不同的置信度下,始终选择黄山旅游、苏宁易购、顺鑫农业这三只股票进行组合投资,投资的股票种类并没有变化,只是投资的比例有所调整。当置信度θ设定为90%时,上述三只股票的投资比例分别为12.36%、28.52%、59.12%,投资者为获得1.61%的周期望收益率,所承担的风险值VaR、CVaR和单位收益风险分别为8.96%、9.28%和5.78。也就是说,有90%的概率可以断定:未来一周内,上述三只股票组合因市场正常波动所导致的损失不超过8.96%,因市场正常波动所导致的极端损失不超过9.28%,为获得1%的收益所承担的极端损失不超过5.78%。
当置信度θ设定为99%时,上述三只股票的投资比例分别为7.19%、19.76%和73.05%,投资者为获得2.02%的周期望收益率,所承担的风险值VaR、CVaR和单位收益风险分别为11.97%、12.13%和6.01。也就是说,有99%的概率可以断定:未来一周内,上述三只股票组合因市场正常波动所导致的损失不超过11.97%,因市场正常波动所导致的极端损失不超过12.13%,为获得1%的收益所承担的极端损失不超过6.01%。
从表3可知,当置信度θ从90%增加到99%时,VaR值从8.96%上升到11.97%,CVaR值从9.28%上升到12.13%,也就是说,VaR值和CVaR值都伴随着置信度θ的增加而上升,这意味着模型对投资组合风险的测度越来越充分,模型求解结果的可信度也越来越强。
同时,从表3中不难发现,在三种置信度下,CVaR值比VaR值都高,这反映出CVaR对投资组合极端风险的刻画要比VaR更加充分,也进一步证实风险测度方法CVaR比VaR更完善。此外,当投资者期望收益率增加时,投资者承担的风险值VaR、CVaR和单位收益风险也不断上升,也印证了“高收益高风险”的投资规律。
四、结论
本文以CVaR与期望收益率的比值来度量单位收益风险,通过引入投资组合收益率的偏度大于等于零约束来降低投资损失发生的概率,构建出偏度约束下单位风险最小的投资组合优化模型,并利用我国沪深两市股票数据对模型进行了实证检验。
与传统的投资组合模型相比,此模型的主要特色体现在:(1)不需要投资者事先设定收益率就能求解,既满足了部分投资者对收益率没有特定要求但期望赚取每一元钱所承担风险最小的需求,又对投资组合的收益与风险加以综合考虑,可以避免投资者对收益率设定得过高或过低所导致的单位收益风险偏高,减少了投资者对收益率的事先盲目估计行为,提高了投资的效率和合理性。(2)通过引入偏度大于等于零的约束,减少了重大投资损失发生的几率,同时保留了高收益率发生的概率,降低了投资风险。(3)对模型作离散化和线性化处理,不需假定收益率是否服从正态分布就能求解,既简化了模型的计算,又拓宽了模型的适用范围。

