身边的概率统计之小概率原理
徐英 徐雅静



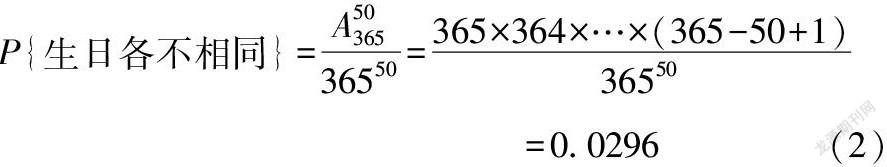


摘 要:小概率原理是统计推断理论中一个重要的基本原理,常常被广泛地应用于人们的日常生活和工作中.本文通过生动的故事案例,简述了小概率原理的基本概念和特点,概括了小概率原理在生活中应用的方法和技巧,引导人们正确认识和处理身边的小概率事件,运用小概率原理科学指导我们的行为,从而有效地规避风险,把握机遇。
关键词:统计推断;小概率事件;小概率原理;应用
中图分类号:O212 文献标识码:A
Abstract:As a very important basic principle in the inferential theory of statistics,the small probability principle is extensively applied to people’s daily lives.By some vivid stories and cases,this paper is devoted to describing the definition,features and applications of the small probability principle.It leads people to handle small probability events properly,and guides people’s behaviors scientifically.Therefore,opportunities would be seized and risks can be avoided.
Keywords:Statistical inference;Small probability events;The small probability principle;Applications
1 概述
小概率原理作为统计推断理论中的一个重要基本原理,常常在不经意间指导人们的行为,因此被广泛地应用到日常生活和工作中。乘车出行有时可能会发生事故,但是为什么会归心似箭乘车回家探亲或者兴致勃勃乘车出门旅行呢?购买两元一张的体育彩票有可能中500万大奖,为什么不争先恐后地去买呢?很多人会这样回答:“一次乘车出事故的概率太小了,不用担心;买彩票中大奖的可能性也太小了,一张彩票中大奖几乎是不可能的。”是的,这个回答已经在用“小概率原理”了。
事实上,小概率原理是指“小概率事件在一次试验中几乎是不会发生的”[1],是人们在长期的生活实践中总结和归纳出来的一条具有较强实用性的原理。因为“一次乘车出事故”与“买彩票中大奖”均为小概率事件,根据小概率原理,它们在一次试验中发生的可能性非常小,认为是几乎不可能发生。
在日常生活和工作中,不确定性给人们带来许多麻烦。无论是股市的涨跌、某类事故的发生,还是自然灾害的降临,在面对机遇或风险等随机问题需要做出推断和决策时,“小概率原理”常常是人们解决问题的有效手段甚至唯一手段。因此,这个原理又被称为“实际推断原理”。
那么,多小的概率才能称为小概率呢?这不能一概而论,要因人、因地、因事而异,正如人们常说的“这蚂蚁真大”“这大象太小”一样,大家要做的是让蚂蚁和蚂蚁比,大象和大象比。比如,一批铅笔的次品率为1%,可以出售,但一批注射用的针药有1%不合要求,就不能出售,因为它会对人的健康造成危害。通常情况下,将概率小于等于0.05的事件称为小概率事件。
除了在乘车或购买彩票时,大家在不经意间运用了小概率原理外,对于日常生活、工作中让人们感到困惑和费解的许多事情,只要善于从概率的角度做认真的思考,合理运用小概率原理,都可得到比较深刻的结果。本文通过简单生动的故事和案例,使人们能够注意到身边的概率统計,了解小概率事件和小概率原理的基本概念和特点,学会运用小概率原理科学指导自己的行为,从而能够有效地规避风险,把握机遇,实现“在危机中育新机、于变局中开新局”[2]。
2 小概率原理的直接应用
2.1 摸彩球游戏
人们经常见到街头摸奖的游戏,比如下面的摸彩球游戏[3]。一个口袋中装有6个红球与6个白球,除颜色不同外,12个球完全一样,每次从袋中摸6个球,游戏的规则见下表1。
从表面上看,表1中7种情况只有一种是输的,而其他六种情况都是赢的,这会让很多人动心,以为天上真的会掉下馅饼,然而游戏的玄机就在于这7种结果的发生不是等可能的。为了弄清楚这个问题,现计算表1中7种情况发生概率。
在无法区分红球和白球的情况下,任意摸6个球,摸到i个红球和j个白球的概率属于大家学过的古典概率,于是有:
根据公式(1),得各种情况发生的概率如表2所示。
从表2可以发现,赢得100分或者50分都是小概率事件,在一次摸取中几乎是不会发生的,虽然大约有48.7%的概率可以赢得20分,但是,却有43.3%的概率要输掉100分,也就是有近一半的机会要输掉100分,因此,摸的次数越多,输的就越惨。
事实上,这是一种“机会游戏”,庄家利用小概率原理,使得中大奖的概率达到很小。因此,庄家肯定是要赢的,玩的人越多,庄家赢的就越多。这就告诉人们,遇到诱惑时,要谨慎行事,要警惕这些利用小概率原理设置的陷阱,正确认识小概率事件,在生活中趋利避害。
2.2 生日游戏
我们来做一个生日游戏:一位同学新到一个班级,他完全可以面对49名新同学,做一个惊人的宣布:“大家好,班上一定有两名同学的生日是相同的!让我们认识一下他们,并为他们祝福吧!”大家一定会惊讶不已!一年有365天,而班上只有50名同学,难道生日会重合吗?实际上,这是极可能获得成功的。
根据古典概率的计算方法,全班50名同学生日各不相同的概率为:
公式(2)的分母是50名同学在一年内生日的所有可能情况,也就是365的50次方,分子是50名同学生日各不同的所有情况,即365天任取50天的排列数A50365。
可以发现,“全班50名同学生日各不相同”是个小概率事件。根据小概率原理,在一次游戏中它几乎是不会发生的。因此,推断班里面至少有两个人的生日相同是合理的。巧妙地运用小概率原理,还可以给人们的生活增添很多乐趣。
2.3 女士品茶与实验设计
20世纪20年代末一个夏日的午后,在英国剑桥,一群学者和他们的夫人们正在一起享用下午茶,一位女士坚称:把茶加进奶里,或者把奶加进茶里,不同的做法,会使茶的味道品起来不同。
在场的科学精英们对那位女士的“胡言乱语”嗤之以鼻,他们难以想象,仅仅是因为加入奶、茶的顺序不同,就会使茶的味道品起来不同。但是,一位身材矮小、戴着厚厚的眼镜、蓄着的短胡须的先生,却不这么认为,他对这个问题很感兴趣。他兴奋地对大家说:“让我们一起来检验这个命题吧!”[4-5]
于是,在胡须先生的指导下,他们讨论出了试验检验的若干种方案。其中有这样一个方案:把8杯已调制好的茶放到那位女士的面前,告诉这位女士4杯是先加茶后加奶,4杯是先加奶后加茶的。不过,排放的顺序是随机的,看看这位女士能否正确地品尝出不同的茶。试验结果是该女士完全正确地从8杯中品尝出了不同的茶。根据此试验结果可以断言该女士具有分辨能力吗?
我们假设“该女士没有分辨能力”,利用小概率原理,结合观测结果,来推断是否否定该假设,进而判断女士是否具有“分辨不同调制顺序的茶”的能力。
在原假设为真时,即女士无分辨能力,该女士从8杯中挑出4杯“先放牛奶后放茶”的方法,与随机从8杯中挑选出4杯是一样的。因此根据古典概率的计算公式,可以得到女士能正确品尝出不同的茶的概率为:
这是一个小概率事件,根据小概率原理——认为小概率事件在一次试验中不会发生,所以针对这一次试验设计,我们有理由否定原来的假设“女士没有分辨能力”,认为女士具有“区分不同调制顺序的茶”的能力。这里我们是将小于0.05的概率定为小概率,在假设检验中通常称其为显著水平。
事实上,有些试验者会认为0.05的显著水平不合适,希望将显著水平修改为0.01,那么在新的显著水平下,我们就没有充分的理由否定原假设“女士没有分辨能力”。这时我们可以对试验做些修改,将8杯改为10杯,并且不告诉女士“先加茶后加奶与先加奶后加茶各有4杯”的事实。原假设仍然为“女士没有分辨能力”。
在原假设为真的条件下,该女士只能通过猜测来回答每杯茶的调制顺序,所以每杯猜对的概率为0.5,记X为女士猜对的总杯数,显然X~B10,0.5。则有
PX=8|原假设为真=C8100.58·0.52=0.044
PX=9|原假设为真=C9100.59·0.51=0.0098
PX=10|原假设为真=C10100.510·0.50=0.00098
可见,10杯中猜对8、9、10杯的概率分别为0.044、0.0098、0.00098。也就是说如果试验结果为那位女士猜对了9杯或10杯,那么在0.01的显著水平下,就有理由否定原假设,相对上一个试验,这次试验否定“该女士没有鉴别能力”的证据要有力得多。所以我们可以推断她所说的“饮品味道与加入茶、奶的先后顺序有关”是可信的。
正是这个夏日午后的女士品茶使那个留着短胡须的先生突发灵感,将检验女士品茶能力的多种试验方案写入了他的开创性著作《试验设计》中。这位短胡须先生就是英国20世纪最有成就的统计学家罗纳德·艾尔默·费歇尔(Ronald Aylmer Fisher),作为概率论与数理统计的奠基人之一,他在《试验设计》中给出了对后世影响深远的科学试验设计思想,对概率论和数理统计的发展做出了巨大的贡献。
结语
通过以上实例,相信大家已经感受到小概率原理与人们的生活息息相关。值得注意的是,小概率事件不是不可能事件,虽然在一次试验中小概率事件几乎是不可能发生的,但是也不能忽视小概率事件,小概率事件重复的次数多了,迟早发生的可能性就會变得很大。
如果在一次试验中事件A发生的概率设为p,不管p如何小,把试验不断独立重复地做下去,n次试验中事件A至少发生一次的概率为1-(1-p)n1-(1-p)n,当n趋向无穷时,这个概率趋向于1。这表明事件A迟早要发生的概率是很大的。比如,在城市闹区乱放鞭炮,就一次而论,引起火灾的可能性并不大,但如果很多人都这样乱放鞭炮,那么“引起火灾”这个随机事件发生的概率就变得很大。常言道“常在河边走,哪有不湿鞋”,这也是基于上述推理。
正确对待“小概率事件”是人们处理工作和生活问题必备的科学素养。不当地忽视“小概率事件”,可能会因麻痹大意而酿成恶性事故。但也不必过分惧怕“小概率事件”,以致谨小慎微,裹步不前。事实上,大家不必因担心天上的飞机掉落在头上而忧心忡忡,但更不可因疏忽大意使飞机的安全受到威胁。
在日常的生活和工作中,大家做任何事情都要脚踏实地,面对生活中的随机事件要理性地分析、对待。正如一位哲学家所说的“概率是人生的真正指南”,只有学会用概率的思想去面对随机问题,才能把握大概率的机遇,规避大概率的风险,从而实现“在危机中育新机,于变局中开新局”[2]的创举。
参考文献:
[1]徐雅静,等.概率论与数理统计[M].北京:科学出版社,2015:196.
[2]人民日报评论员.在危机中育新机、于变局中开新局[N].人民日报,2020-05-25.
[3]秦秉杰.小概率原理及其应用[J].太原学院学报(自然科学版),2019,37(3):18-21.
[4]戴维·萨尔斯伯格.女士品茶:统计学如何变革了革命[M].刘清山,译.南昌:江西人民出版社,2016:3.
[5]陈希孺.数理统计学简史[M].长沙:湖南教育出版社,2000:226.
课题:郑州轻工业大学第13批教学改革与研究项目:“大学数学”新形态教材与资源建设的研究与实践——以“概率论与数理统计”课程为例
作者简介:徐英(1982— ),女,汉族,山东菏泽人,博士,讲师,研究方向:应用微分方程;徐雅静(1963— ),女,汉族,山东茌平人,硕士,教授,研究方向:应用统计分析。

