谈中学物理问题解决中图像法对科学思维的培养

张俊

(江苏省南通市通州区教师发展中心)

图像是物理学科中用来直观形象描述物理现象或物理规律的常用手段,运用函数图像进行实际物理问题的分析是中学物理教学中的热点问题.运用图像法解决物理问题既直观又方便快捷,可以培养学生处理信息的能力、分析解决问题的能力、进行科学论证和科学推理的能力,使他们形成科学思维,促进物理学科核心素养所必需的适应个人终身发展和社会发展的必备品格与关键能力的形成.

1 利用斜率的物理意义，巧判图线趋势

1.1 图线上每一点的斜率

例1如图1所示,定值电阻R0与滑动变阻器R串联,在滑动变阻器的滑片P移动过程中,电表读数与变阻器连入电路部分阻值之间的关系可能符合下列图中的().

图1

分析该题可以首先定性判断,当R增大时,电压表的示数也会增大,可以排除C、D 选项,如何确定A、B选项哪一项正确呢? 可以在图线上任取一点,该点的斜率k＝即为流过电阻R的电流,而实际情况下,当R增大时,电流会逐渐减小,所以图线上点的斜率会逐渐减小,如图2所示,因此选项B是正确的.

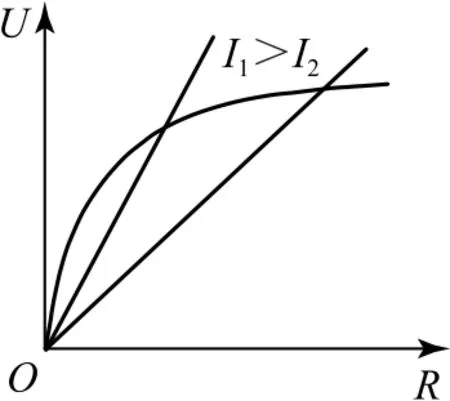
图2

1.2 图线上每一点切线的斜率

例2如图3所示,不可伸长的轻绳一端固定于O点,另一端连接一质量为m的小球,将小球拉至与O点等高,细绳处于伸直状态的位置后由静止释放,经时间t轻绳转过的角度为θ.在小球由静止释放到运动至最低点的过程中,下列关于小球重力势能Ep(取最低点为零势能点)随角度θ变化、动能Ek随时间t变化的图像中,可能正确的是().

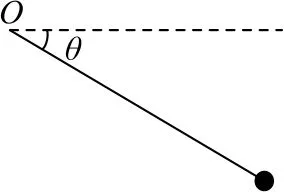
图3

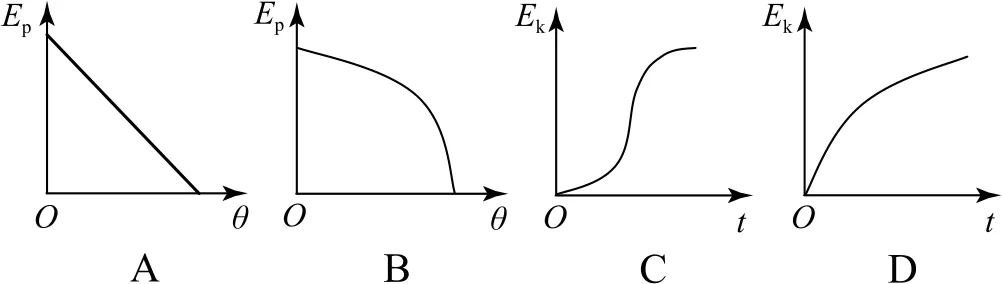
分析小球的重力势能Ep＝mgL(1－sinθ),因此图像应该是函数sinθ沿y轴向上平移mgL后所得到的图像,选项A、B都不正确;明确小球的动能Ek随时间t如何变化是解决本题的关键.因为小球摆下时合力做功,即为重力做功,所以小球动能的变化等于重力所做的功,因此图线上每一点的切线的斜率表示的物理意义为k＝,即为小球重力做功的瞬时功率,小球在与O点等高的位置和最低点时,重力的瞬时功率均为0,故而图线切线的斜率应该先增大后减小,只有选项C是正确的.

点评

上述两个问题中,均要判断图线弯曲的趋势,这类问题的突破口往往可以从图线上每一点的物理意义及其变化趋势、图线上每一点的切线斜率的物理意义及其变化趋势进行判断分析.

2 通过图像还原物理情境、过程，建立物理模型

2.1 单一过程问题

例3一款新能源电动汽车在某次测试中速度从0增加到30m·s－1的加速时间为10s,测试过程中车的加速度随速度的增加而逐渐减小,分析汽车在该段时间内运动的位移大小与150m 的关系.

分析根据题意,画出汽车在10s内运动的速度v随时间t变化的关系图像如图4所示,因为车的加速度逐渐减小,所以图线的斜率也逐渐减小.用虚线连接图线的两个端点O、A,易知线段OA与横坐标所围三角形的面积为150 m,所以汽车在该时段内运动的位移大于150m.

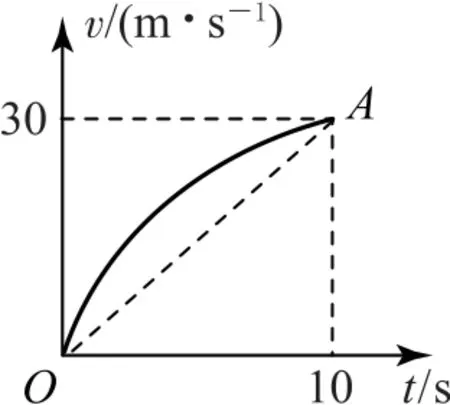
图4

点评

该题通过画出v-t图线较为直观地反映出汽车在10s内运动的情况,建立加速度逐渐减小的加速运动的物理模型,根据图线与坐标轴所围图形的面积判断汽车运动的位移大小关系.

2.2 复杂的多过程问题

例4如图5-甲所示,长为L的两块导体板水平平行放置,大量质量为m、电荷量为e的电子由静止开始,经电压U0的电场加速后,连续不断地沿平行板的方向从两板正中间射入两板之间.当两板均不带电时,这些电子通过两板之间的时间为T(T未知),现给两板间加上如图5-乙所示的幅值恒为U1的周期性电压(电子重力不计).

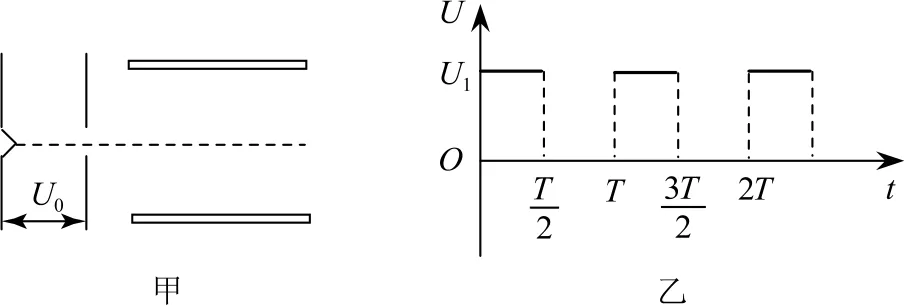
图5

(1)为保证有电子能从两板间穿出,求两平行导体板间的最小距离d1;

(2)若所有电子均能从两板间穿出,求两平行导体板间的最小距离d2.

分析该题中,分别画出粒子在t＝0、t＝时刻进入偏转电场后垂直于导体板方向的速度随时间变化的关系图像如图6 所示,对应图线①的粒子在偏转电场中有最大的侧移量,对应图线②的粒子在偏转电场中有最小的侧移量,所以为保证有电子从两板间穿出,板间距离的一半应该大于②中的粒子的最小侧移量,即以t＝(n＋)T(n＝0,1,2,…)时刻进入偏转电场的电子的运动为临界情况;而要所有的电子均能从两板间穿出,板间距离的一半最小为①中的粒子的最大侧移量,即在t＝nT(n＝0,1,2,…)时刻进入偏转电场的电子的运动为临界情况.

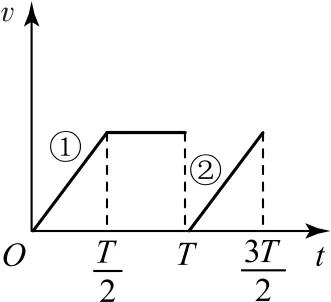
图6

点评

物体运动过程中分析运动的距离关系问题时,可以画出v-t图线,根据图线的面积等寻找解题的思路,由于速度是矢量,要注意其方向,注意t轴与图线所包围图形面积所表达的物理意义.

3 根据图像简化数学表达，确定变量关系

例5光敏电阻是制作传感器的常用元件.如图7为某光敏电阻的控制电路,电源电压U0恒定,内阻不计,RG为光敏电阻,其阻值随空气透光程度的变化而变化,R0为定值电阻.为监测空气的透光程度,现将电压表表盘的电压刻度值转化为对应的总阻值(R0＋RG),则转化后表盘上从左到右相邻两刻度线对应阻值的减小量将如何变化?

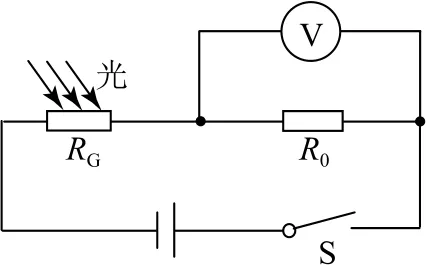
图7

分析由闭合电路欧姆定律可知U0＝I(R0＋RG),电压表示数U＝IR0,由此可以解得,所以电压U与(R＋RG)成反比,作出U-(R＋RG)图线(双曲线)如图8所示,并在U轴上取电压差值相等的三点Ua、Ub、Uc,向横轴作对应的垂线,可以推断出,随着电压的增大,转化后表盘上从左到右相邻两刻度线对应阻值的减小量将逐渐减小.

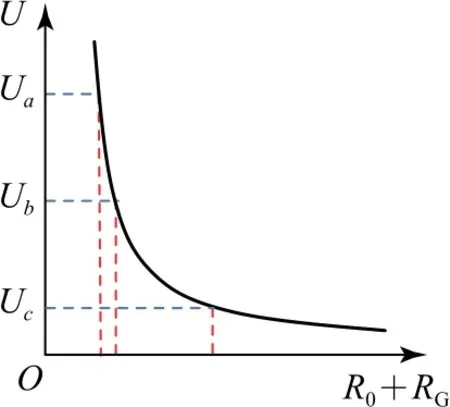
图8

点评

本题若采用函数关系式进行推断会很烦琐,而根据物理规律推导出物理量之间的函数关系,画出图像定性讨论变化量之间的关系,既直观又简洁,充分体现出了图像法解决问题的优越性.

4 画图分析图线交点，找寻等量关系

例6图9-甲是模拟空调温控装置原理的简化电路,电源电动势为6V,内阻不计,R1为电阻箱,L为阻值不计的线圈,R2是热敏电阻,其阻值随温度的升高而减小,当控制电路中的电流大于等于某一值时,接通受控电路使空调工作.当电阻R1调到1kΩ时,能接通受控电路.已知热敏电阻的电流随电压变化的I-U关系图像如图9-乙,求此时控制电路中的电流.

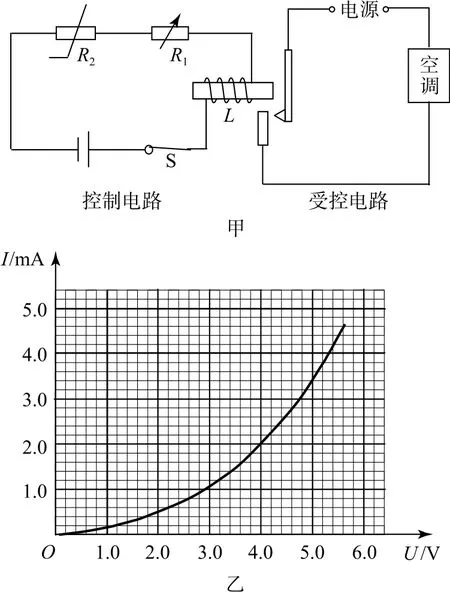
图9

分析在I-U关系图线中画出表示电阻R1的IU图线,如图10所示,由图可知,当电流为2mA时,电阻R1上的电压为2V,热敏电阻R2上的电压为4 V,说明控制电路中的电流即为2mA.

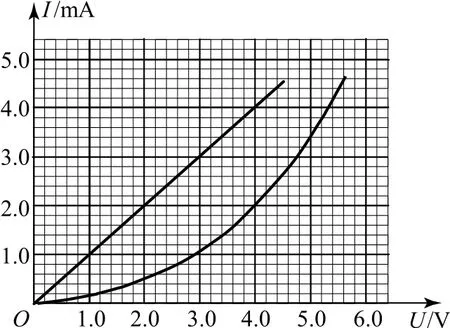
图10

从以上的分析可以看出,应用图像解决物理问题,是借数学之“形”,析物理之“质”,可以较为形象、清晰地呈现物理量之间的关系,把文字叙述、符号表达转化为图形表征,培养了学生应用数学知识解决物理问题的能力,培养了学生的推理论证能力,锻炼了学生的科学思维,提升了学生的学科核心素养.

当然,图像在中学物理中的应用还有很多,除了本文所分析的问题外,还可以利用函数图像的截距、拐点、峰值等来解决物理问题,像物理问题中的平均值、坐标变换化曲为直等也都蕴含着丰富的物理思想和科学思维,颇具研究和总结的价值.

(完)