基于随机森林模型的动态动脉血管硬化指数估计方法*

张海康，程云章，张天逸

(上海理工大学 上海介入医疗器械工程技术研究中心，上海 200093)

引言

根据世界卫生组织发布的《2020世界卫生统计报告》，仅在2016年，全球因非传染性疾病(noncommunicable diseases，NCDs)导致的死亡就达到了4 100万，约占当年全球总死亡人数的71%。心血管疾病(cardiovascular diseases，CVDs)，作为NCDs中主要疾病之一，每年造成的死亡数量约为1 700万[1]。动脉粥样硬化心血管疾病(atherosclerotic cardiovascular disease)和动脉纤维性硬化性心血管疾病(arterioscleroticcardiovasculardisease)是心血管疾病中造成诸多脏器障碍甚至病变的重要原因之一。在动脉粥样硬化早期，其临床症状不明显。若能在早期及时发现并对患者进行有效地治疗，可显著减缓病情恶化的程度[1-2]。

传统的大动脉弹性功能检测的方法包括：动脉脉搏波传导速度 (pulse wave velocity, PWV)和超声检测内膜-中层厚度 (intima-media thickness, IMT)。动脉的脉搏波传导速度能间接反映大动脉的扩张性。高分辨率超声既可以通过观察动脉某一横断面压力和动脉内径的变化关系反映动脉弹性的改变，又可以检测颈动脉内膜-中层的厚度，是早期诊断动脉粥样硬化的重要依据。但是，以上两种检测手段都需要昂贵的检测设备及专业的操作人员，在大规模的临床实践和流行病学研究中难以广泛推广。因此，研究更为简单有效的检测手段具有现实意义[4]。

2006年，李燕等[3-4]首次提出了AASI这个能反映动脉血管弹性的指数，并与传统的反映动脉血管弹性的指标进行了相关性分析，包括了脉搏波传导速度、中心增强指数、外围增强指数。之后，开展了一些关于AASI的研究。Palmas等[5]比较了AASI和24 h脉压尿液白蛋白排泄的相关性。Daolan等[6]比较AASI以及脉压对心脏性死亡以及中风的预测表现。结果显示，AASI作为对中风的预测因子优于脉压差，在心脏性死亡的预测上，脉压要优于AASI，而在正常血压区间内，两者都无法作为独立的心脏性死亡或者中风的预测因子。Eniksen等[7]发现AASI对于中年人群的肾小球滤过率 (glomerular filtration rate, GFR)下降是一个重要的独立因素。Obata等[8]研究了脑血流自动调节下限(lower limit of cerebral autoregulation，LLA)与AASI之间的关系，发现LLA与AASI关系显著，AASI可以作为术中预测LLA阈值的重要工具。

尽管学者们对AASI做了大量的研究，但大部分的研究都停留在临床数据统计与对AASI表征生理信息的验证上。AASI作为一个获取难度相对较低的能反映心血管健康状况的生理指标，对于AASI的实际应用成果却不多。因此，本研究基于动态动脉硬化指数 (ambulatory arterial stiffness index, AASI)，提出了一种新的测量患者动脉硬化程度的方法。作为一种动脉硬化的早筛方法，该方法能有效地降低测量成本，并对后续的临床诊断和检测具有一定的参考意义。与传统的血管弹性探测方法相比，基于机器学习得到的AASI估计值无需超声诊断装置或者侵入式探测，降低了重要生理信息获取的难度，对心血管疾病的早筛有重要意义。

1 材料与方法

基于机器学习的动态动脉血管弹性指数的估计流程图，见图1。

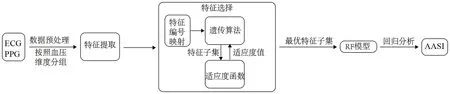
图1 AASI估计系统流程图

1.1 动态动脉硬化指数(AASI)

早在20世纪初，一些研究已经注意到收缩压和舒张压的变化可以反映动脉血管的弹性功能。当一个人的动脉血管健康有弹性时，收缩压升高，舒张压也相应地升高；当血管弹性降低后，收缩压增高，而舒张压增高不明显、甚至降低。这说明收缩压和舒张压两者之间的动态变化关系在一定程度上反映动脉的弹性功能。收缩压和舒张压的对应数值，可以分析舒张压和收缩压这之间的回归关系。李燕等把一段时间内采集得到的收缩压与舒张压做回归分析，其中收缩压作为自变量，舒张压作为因变量。AASI的计算方式为1减去回归斜率b。动脉弹性好，则AASI趋近于0；动脉弹性僵硬，则AASI趋近于1[3-4]。AASI的数学表达式见式⑴、式⑵：

DBP=a+b×SBP

(1)

AASI=1-b

(2)

其中，DBP代表一个心动周期的舒张压，SBP代表一个心动周期的收缩压。a、b是回归方程的回归系数。

1.2 数据源

本研究所用公共数据库来自于UCI机器学习资料档案库(UCI Machine Learning Repository)中的无袖带式血压估计数据集。该数据集实质上是经过去噪处理后的MIMICII(multi-parameter intelligent monitoring intensive careII)数据集[9-10]。数据集包含125 Hz的从指尖获取的光电容积脉搏波(PPG)信号、125 Hz的有创动脉血压(ABP)信号、125 Hz的心电信号(ECG)。其中，由于MIMICII数据库自身带有相当可观的危重患者的数据，血压处于极高值或极低值的病例被移除(SBP≥180 mmHg,DBP≥130 mmHg)∩(SBP≤80 mmHg,DBP≤60 mmHg)。此研究所使用的数据集基本信息见表1。在本研究中，80%的样本(共计2 036例患者数据)被用于模型的训练；20%的样本(共计510例患者)被用于模型的测试。

表1 所用数据集的基础信息

1.3 特征提取

特征提取是机器学习中最重要的部分之一。根据Sharifi等所做的研究[11-15]，本研究一共选用了13个特征。由于源信号PPG和ECG是时域信号而AASI则相对是一个常值，因此,本研究中所有的时域信号皆以在整个时轴上的均值呈现，以此使输入信号与被估计值得以匹配。整个特征提取过程在Matlab R2020a平台上实现。表2是所用全部特征名,图2—图4是对信号的提取特征过程。

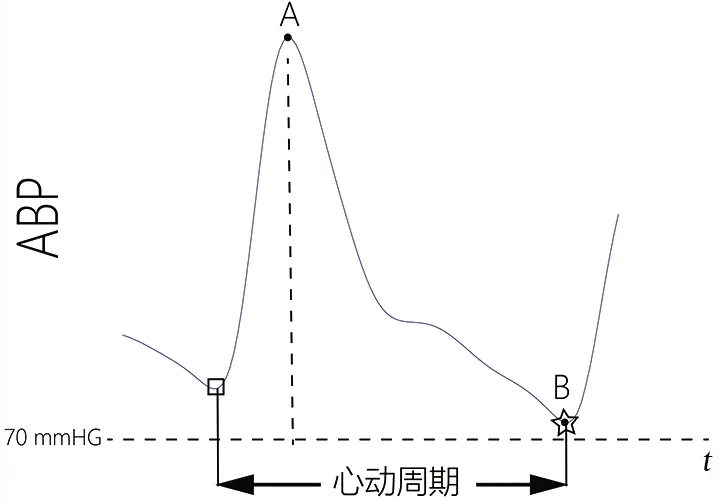
注：A和B作为周期内的最大值和最小值，被定义为是一个心动周期内的收缩压以及舒张压。

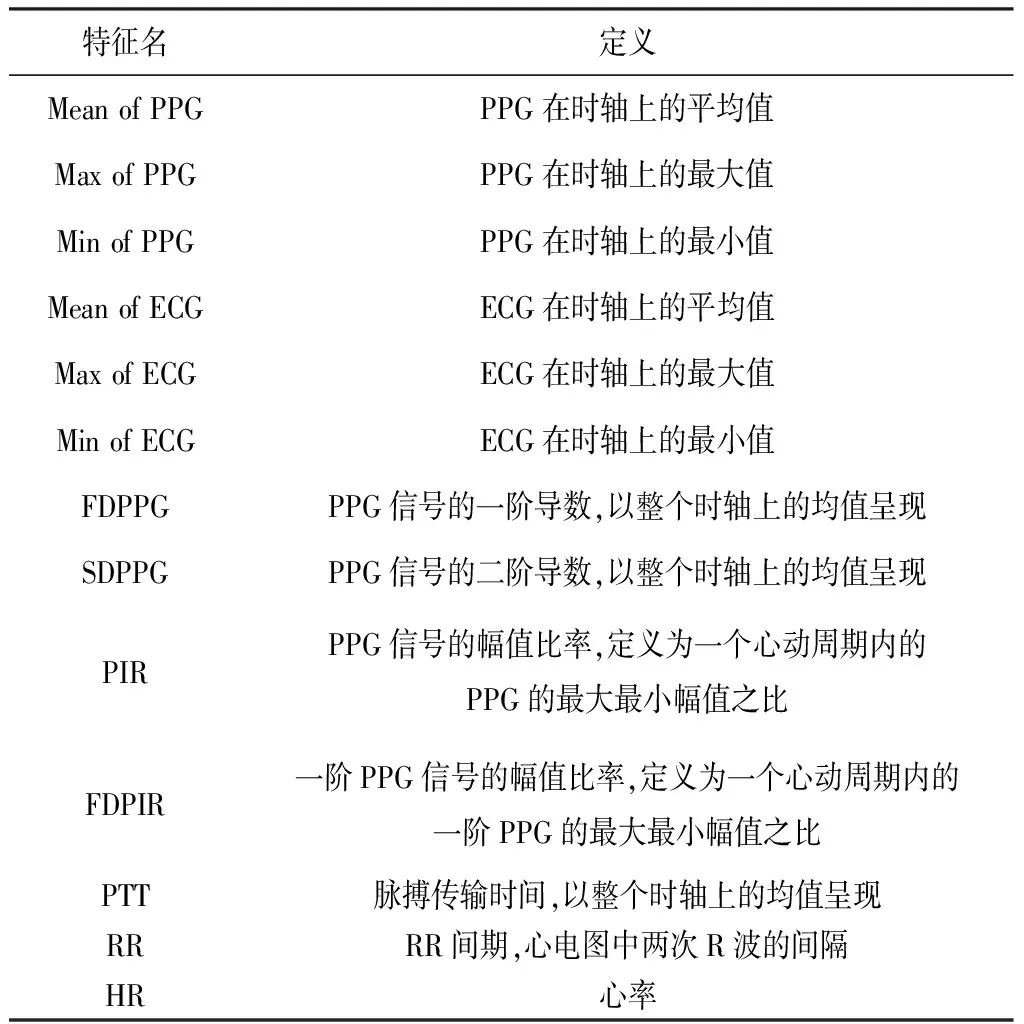
表2 特征名及其定义

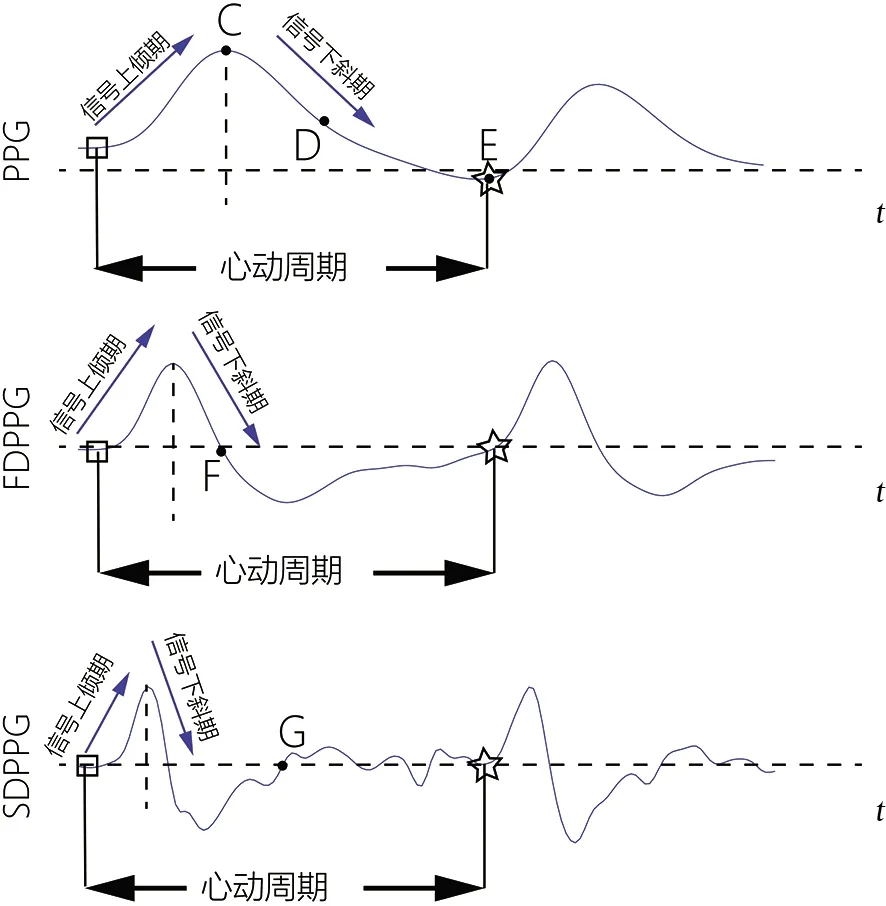
注：C和E是一个心动周期内的PPG最大值和PPG最小值； D是PPG信号这个周期的均值；F和G是FDPPG和SDPPG的均值。图3 PPG信号及其衍生的FDPPG和SDPPGFig.3 PPG, FDPPG and SDPPG

1.4 随机森林回归

随机森林(random forest ，RF)回归是由决策树学习衍生而来的。即使特征与目标呈非线性关系，RF也能有效地估计输出。RF算法采用bootstrap分类器来估计响应变量。它将每一组决策树模型都与数据集进行匹配。每棵树都使用训练数据不同的bootstrap样本训练，以此作为自己的回归函数，由回归给出的最终输出与各个决策树输出的平均值对应，即为RF纠正决策树算法常见的过拟合现象的过程。而未进入bootstrap分类器的样本被称为out-of-bag (OOB)样本,它们被用来测试决策树的准确性和评估整体模型的性能[16-20]。

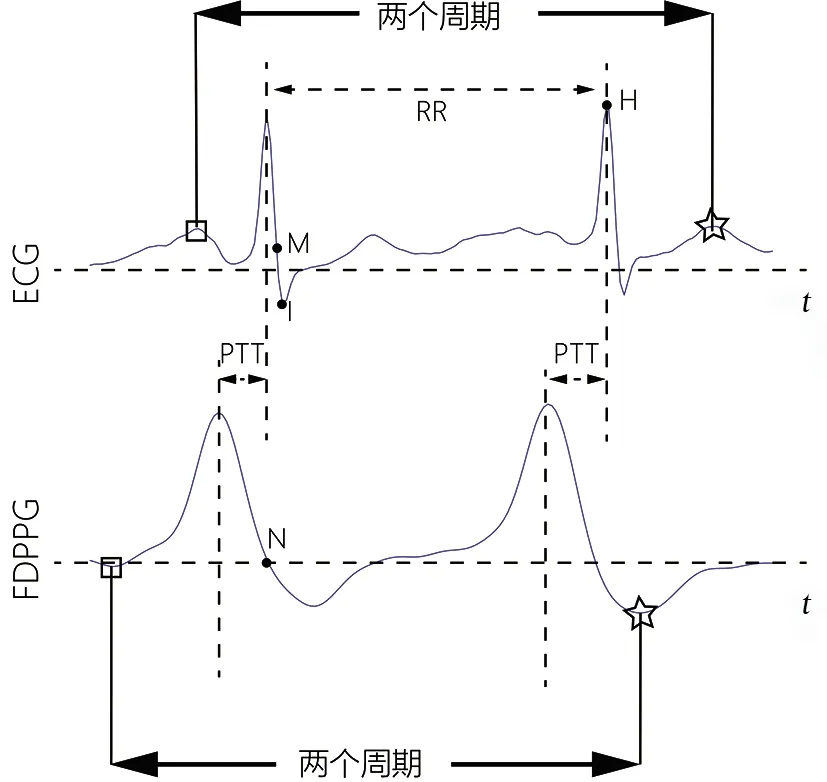
注：H和I是ECG信号的最大值以及最小值。M和N是

整个回归过程在Matlab平台上使用Treebagger函数完成。其形式见式(3)：

B=Treebagger(NumTrees,X,y)

(3)

其中，AASI作为响应y，不同形式的特征组合作为输入X，树的数量(NumTrees)设置为100。

1.5 遗传算法

表2中的13个特征的组合将被作为RF模型的输入。但若使用遍历思路解决该特征筛选问题，将会有213-1轮RF模型计算。考虑到整个数据集大小，该思路是不可取的。因此，引入遗传算法(geneticalgorithm,GA)进行特征筛选，以此找到最优特征子集组合[21-25]。

在本研究中，RF模型的平均绝对误差(MAE)作为GA的适应度函数。同时，所有的13个特征均以“0”、“1”的形式表明其被选择与否(“0”代表该特征不被选择。“1”代表该特征被选择)，它们共同组成13位二进制数字作为其特征子集组合编码，以此量化特征筛选问题,见图5。

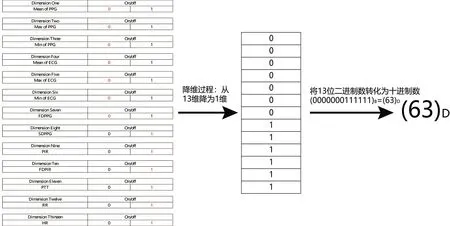
图5 特征子集编码过程

2 实验结果

本研究所用衡量方法的指标是均方根误差(root mean squared error, RMSE)、绝对平均误差(mean absolute error, MAE)、皮尔森相关系数(pearson correlation coefficient,r)和组内相关系数(Intraclass correlation coefficient, ICC)。实验结果，见表3。

表3种挑选了四种经典回归模型进行AASI的估计，全特征输入代表了未经筛选的特征子集组合。其中，脊回归损失函数的正则项系数设定为α=5。由表3可知，随机森林模型在估计AASI问题时误差最小(MAE、RMSE)、估计值与真实值的线性相关程度最高(r)。为了进一步提高本研究方法的性能，引入GA对综合性能表现最好的随机森林模型进行特征子集筛选。

2.1 遗传算法特征筛选

引入GA进行特征筛选，GA的迭代过程见图6。

表3 四种回归模型估计结果

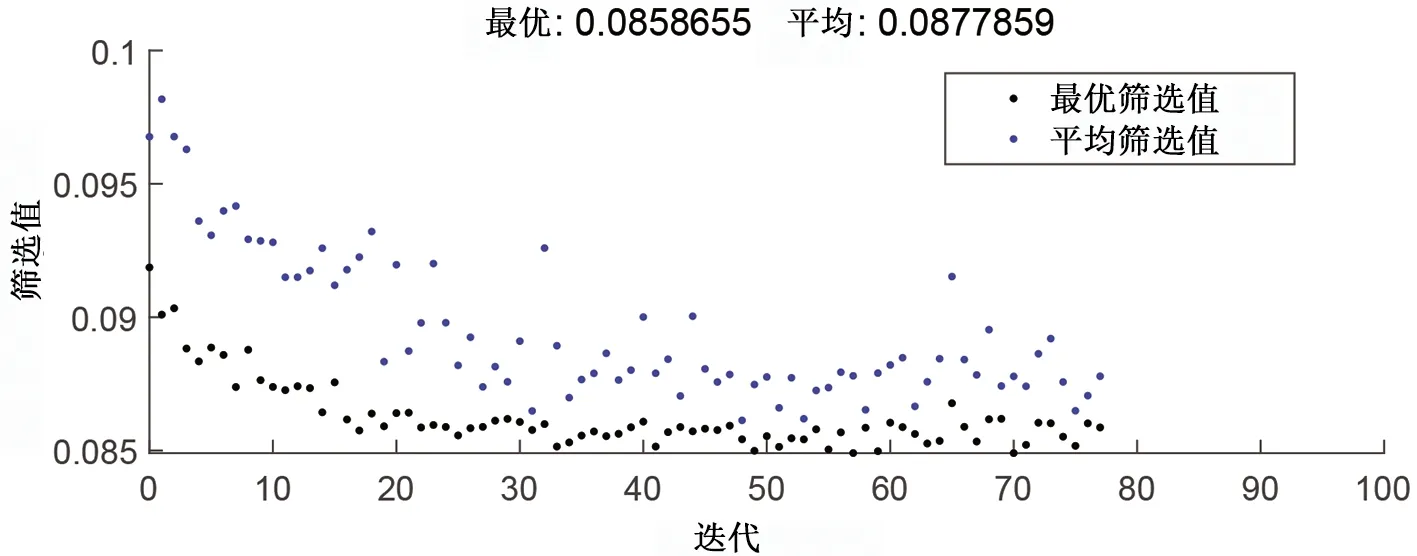
图6 寻找最优特征子集的GA过程

由GA获得的最优特征子集见表4，其估计结果表现见表5。

表4 由GA获得的最优特征子集

2.2 在血压以及心率维度下AASI估计分布情况

为了分析进行过特征筛选后的RF模型对于不同患者的准确度，本研究从血压、心率两个维度对所有样本进行了误差统计，见图7。

图7的横坐标轴代表每个样本的平均动脉血压，纵坐标轴代表每个样本的心率，色块代表绝对误差大小：由浅入深代表绝对误差由大至小。一个黑点代表一个病例，为了使统计结果方便可视，且能展现出总体样本的趋势，在此引入了局部加权回归使图像完整且平滑。

表5 RF模型下经过GA特征筛选与未经过GA筛选的结果对比

3 讨论与总结

由表3可知，随机森林模型在估计AASI时，其综合性能显著优于表中的其他三种模型。由表5可知，当引入GA完成特征筛选后，RF模型估计AASI的能力提高，误差明显减小。

在本研究中，RF模型的最优特征子集为Max of PPG、Min of PPG、FDPIR、HR和RR。

2.2节分析了在最优特征子集和随机森林模型下，AASI的绝对误差在血压和心率维度上的分布情况。由图7可知，AASI估计值的绝对误差在样本平均动脉血压突破了100 mmHg以后，与其呈正相关，在图7表现为色块在横轴上由深入浅地变化，而另一维度心率与估计AASI误差的关系在图7上尚不显著。产生此现象的原因可能为：(1)训练回归模型的样本中，高血压的样本数要低于正常血压的样本数，因此，模型对高血压样本产生的误差大于正常血压区间的样本；(2)AASI对高血压患者的表现要弱于对正常血压患者。根据李燕等[4]的研究，AASI与颈动脉-股动脉PWV的相关系数在面对正常血压患者时为0.51，而面对高血压患者时仅为0.28[26]。

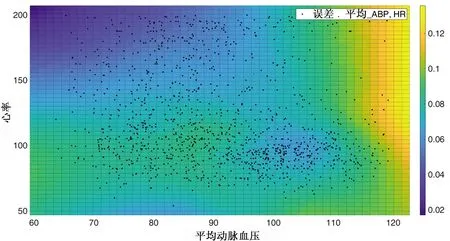
图7 在最优特征子集下AASI误差分布图

为对抗心血管疾病早发的态势，本研究基于动态动脉硬化指数与随机森林模型，完成了动态动脉硬化指数的初步估计，并且优化了在估计过程中的特征选择问题，同时分析了动态动脉硬化指数的估计绝对误差在血压和心率维度上的分布情况。但是模型的可靠性仍需要多中心的外部资料进行验证，并在推广过程中不断优化和提高其性能。