下肢外骨骼康复机器人关节运动轨迹分析与步态测试研究*

魏强生，王殊轶△，肖建如，许炜，邢文琪

(1.上海理工大学医疗器械与食品学院，上海 200093；2.上海市长征医院，上海 200003； 3.中国人民解放军全军骨科研究所，上海 200003)

引言

随着社会人口老龄化进程的加剧，我国由于机体功能衰退或各类致残疾病、事故导致的下肢运动功能障碍患者日益增加。其中由于脊髓损伤导致的截瘫具有较高的发病率，脊髓损伤(spinal cord injury, SCI)发生在第三胸椎以下引发下半身截瘫[1]。截瘫引发的下肢运动功能缺失会带来肌肉萎缩、压疮、神经功能受损等一系列健康问题[2]。

传统的截瘫恢复治疗是由理疗师与患者配合完成，理疗师工作强度大，患者治疗效率低下[3]。下肢外骨骼机器人作为跨领域、多学科交叉融合的产物，现已得到广泛关注[4]。穿戴式下肢外骨骼机器人从生物力学角度进行交互控制设计，充分考虑到运动中存在的生物力学问题[5-6]，达到人体下肢与外骨骼机器人的高度耦合，根据智能化操控对患者运动能力和行走步态进行康复训练，提高患者康复训练的质量和效率[7]。

国内外大量对外骨骼康复机器人的结构优化、仿真分析、运动轨迹规划等的研究成果，已成功应用于运动功能障碍康复领域[8]。美国Ekso Bionics公司研发推出面向截瘫、中风患者助力的下肢外骨骼机器人Ekso[9]，进行了差异化轨迹规划和大量临床分析，可通过行走过程中双腿支撑相和摆动相的差异化特性提供不同控制策略[10]。日本筑波大学联合研制的HAL系列外骨骼机器人推出双下肢、单侧腿和可移动带悬吊支架款等，根据不同术后病情规划康复训练效果最佳的轨迹模式[11-12]。宁萌等[13]采用运动捕捉系统采集下肢运动关节角用于外骨骼闭环控制系统，定义了RMP下肢康复评价标准。陈炜等[14]建立了外骨骼康复机器人动力学模型，并进行了运动轨迹的数据分析和动力学仿真，为控制系统设计提供理论依据。

本研究从运动学建模、动力学建模、虚拟样机技术仿真、样机试制与穿戴步态测试四个方面对下肢外骨骼康复机器人进行分析，从客观角度验证了下肢外骨骼康复机器人的稳定性和有效性。

1 运动学建模与分析

下肢外骨骼机器人由两条机械腿组成，并由髋部连接装置进行连接，总体结构包括穿戴背包、髋关节驱动模块、大腿调节机构、膝关节驱动模块、小腿调节机构、踝关节及足部模块。各构件部分通过连接配合，实现外骨骼机器人髋关节3个自由度，膝关节1个自由度，踝关节2个自由度的空间运动。下肢外骨骼机器人总体设计结构，见图1。

1.集成穿戴模块；2.髋部连接装置；3.髋关节驱动模块； 4.大腿长度调节机构；5.膝关节驱动模块； 6.小腿长度调节机构；7.踝关节及足部模块图1 下肢外骨骼机器人总体结构

为检验模型的正确性和有效性，对构建的下肢外骨骼机器人模型进行运动学建模分析。外骨骼机器人运动学分析主要通过建立基准坐标系和下肢各关节处的坐标系，将下肢各部位简化为执行杆件，并建立相邻关节处坐标系之间的变换矩阵，求解下肢步态运动时关节角度与外骨骼机器人末端执行杆件轨迹之间的关系[15]。

采用D-H法[16]对下肢外骨骼机器人进行运动学建模，对下肢行走过程中生物力学特性进行分析[17]，步态周期中摆动相单腿支撑时受力情况更加复杂，故选择只对右侧单腿进行建模分析，将下肢外骨骼机器人模型简化为在矢状面内运动的连杆模型。简化连杆模型及基准坐标系，见图2。

图2 外骨骼机器人运动学建模

在D-H法中，通常使用连杆长ln、旋转角度θn、偏置长度Dn、转轴公法线距离an等参数来表示建立的运动连杆模型。建立各关节处坐标系OnXnYnZn，其中ln表示连杆n的长度，θ1表示连杆n与连杆n+1之间的旋转角度，Dn表示连杆n与连杆n+1之间的偏置量，an表示相邻连杆转轴公法线之间的垂直距离。各参数见表1。

表1 下肢外骨骼机器人D-H模型参数

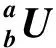
(1)

以髋关节旋转中心为基点建立基准坐标系O0X0Y0Z0，则连杆1到基准坐标系的变换矩阵为：

(2)

连杆2到连杆1的变换矩阵为：

(3)

连杆3到连杆2的变换矩阵为：

(4)

根据计算，P1点的坐标即为：

(5)

P2点的坐标为：

(6)

P3点的坐标为：

(7)

根据计算，即得出了踝关节坐标系原点相对于基准坐标系O0X0Y0Z0的坐标值。

2 动力学建模与分析

动力学分析作为理论力学的一个分支内容，主要研究的是作用于物体的力与运动的关系。下肢处于摆动相运动过程中受力更为复杂，连杆间力与力矩要求更高[18]。现将右侧单腿各运动关节简化为连杆模型，选用拉格朗日方法对下肢外骨骼机器人进行动力学建模，通过得到下肢外骨骼各关节处的角度、角速度、角加速度等[19]，求解各主动关节处运动状态下所需的驱动力及驱动力矩。下肢外骨骼动力学简化模型见图3。

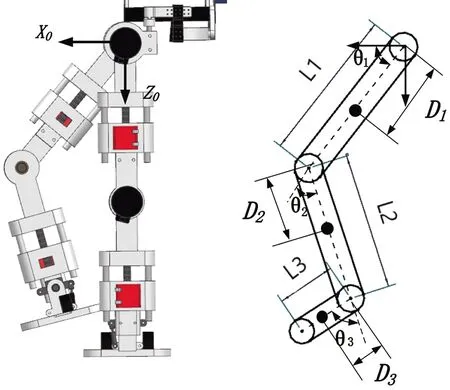
图3 外骨骼机器人动力学建模

拉格朗日方法具有能以简单的形式对较为复杂的系统动力学问题进行求解的优点，对于系统的动能Ek、系统的势能Ep，拉格朗日函数表达式为：

Lg=Ek-Ep

(8)

大腿简化为连杆后质心表达式为：

X1=D1cosθ1

(9)

Y1=D1sinθ1

(10)

小腿简化为连杆后质心表达式为：

X2=D2cos(θ1+θ2)+l1cosθ1

(11)

Y2=D2sin(θ1+θ2)+l1sinθ1

(12)

对于大腿简化连杆的动能、势能计算如下：

(13)

Ep1=m1gD1sinθ1

(14)

设计的下肢外骨骼机器人在踝关节处没有设置电机驱动，因此，在推导动力学方程时，为了简化计算篇幅，将踝关节处转动关节简化为与小腿连杆一体，仅增加质量m3，由此可得简化后的小腿连杆动能与势能：

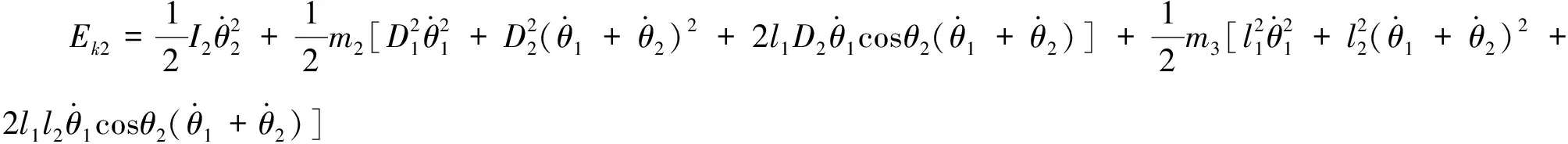
(15)

Ep2=m2g[l1sinθ1+D2cos(θ1+θ2)]+

m3g[l1sinθ1+l2cos(θ1+θ2)]

(16)

以上结果带入到拉格朗日函数表达式中得：

(17)

对下肢外骨骼机器人进行动力学分析，以求解各主动关节处运动时的驱动力与驱动力矩。根据系统拉格朗日方程：

(18)

式中，θi为系统广义上的坐标变量，当系统进行直线运动时，θi为直线运动位移变化量，τi为所有外力之和。当系统进行旋转运动时，θi即为角度变化量，τi为所有力矩之和。

即求得：

(19)

(20)

由此得出，简化连杆模型旋转处，也即髋、膝关节处在步态运动过程中的力矩变化值。

3 虚拟样机技术仿真分析

通过对单侧机械腿进行建模，得出了运动学和动力学理论研究结果。样机试制前，为更好地分析下肢外骨骼机器人系统的运行情况，本节采用ADAMS虚拟样机技术对建立的下肢外骨骼机器人模型进行运动学和动力学仿真[20-21]。将下肢外骨骼机器人模型导入到ADAMS中，重新定义脚部与地面的接触力和各关节处的旋转运动副等[22]，关节处驱动函数参考成年人标准步态数据库clinical gait analysis(CGA)数据和正常与病理功能步态分析资料，考虑到下肢运动功能障碍的患者康复步态行走缓慢，将一个完整的步态周期延长至6 s，在Matlab中进行函数拟合，膝、髋关节驱动函数见图4。

设定仿真时长12 s，步长1 000帧，由于左腿和右腿在步态行走的过程中相差半个周期，因此，接下来只选取右下肢仿真结果进行分析。仿真结束后，进入后处理模块提取左、右足质心在水平步道上的位移，进行曲线拟合(见图5)。

图4 髋、膝关节驱动函数

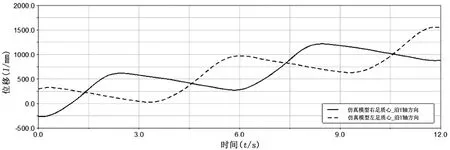
图5 水平方向左右足质心位移

由图5可知，仿真模型左右脚质心水平位移整体呈周期对称变化，通过提取右足前端相对于髋关节质心的轨迹变化，得出仿真输出结果与理论计算结果偏差总体处于合理范围内，验证了模型运动学理论计算的正确性，满足人体下肢行走步态规律，符合设计要求。

前文动力学分析理论计算结果表明，如需得出旋转关节处力矩，需要输入旋转关节处角度、角速度、角加速度等数据。参考成年人标准步态数据库，在Matlab中进行函数计算，得到下肢髋、膝关节步态周期中角度、角速度和角加速度的变化曲线，见图6。

在ADAMS仿真后处理模块中获得外骨骼右下肢髋、膝关节仿真驱动力矩曲线图，导出至Matlab中与理论计算得到的关节驱动力矩曲线进行对比，见图7。

由对比结果可知，髋、膝关节驱动力矩曲线拟合总体趋势较为吻合，绝大部分波动均处在合理范围内，验证了理论建模分析的正确性和仿真分析的有效性，为后续驱动电机选型和样机生物力学特性优化提供了支撑。分析髋、膝关节在拟合曲线多处波峰数值差距较大的原因为：外骨骼机器人仿真过程中参照实际情况设置了与地面的阻尼、接触力和摩擦力等，在足部与仿真步道接触时产生刚性冲击，力矩值发生突变；此外，理论建模分析时，将外骨骼模型简化为连杆结构，而在仿真过程中外骨骼机器人模型贴合人体下肢，结构较为复杂，造成了仿真结果与理论值的差异。

4 样机试制与穿戴步态测试

4.1 外骨骼样机试制

基于建立的符合人体下肢生物力学特性外骨骼机器人三维模型和对简化连杆模型进行的运动学、动力学理论分析及仿真，现已完成样机试制及装配，穿戴效果见图8。

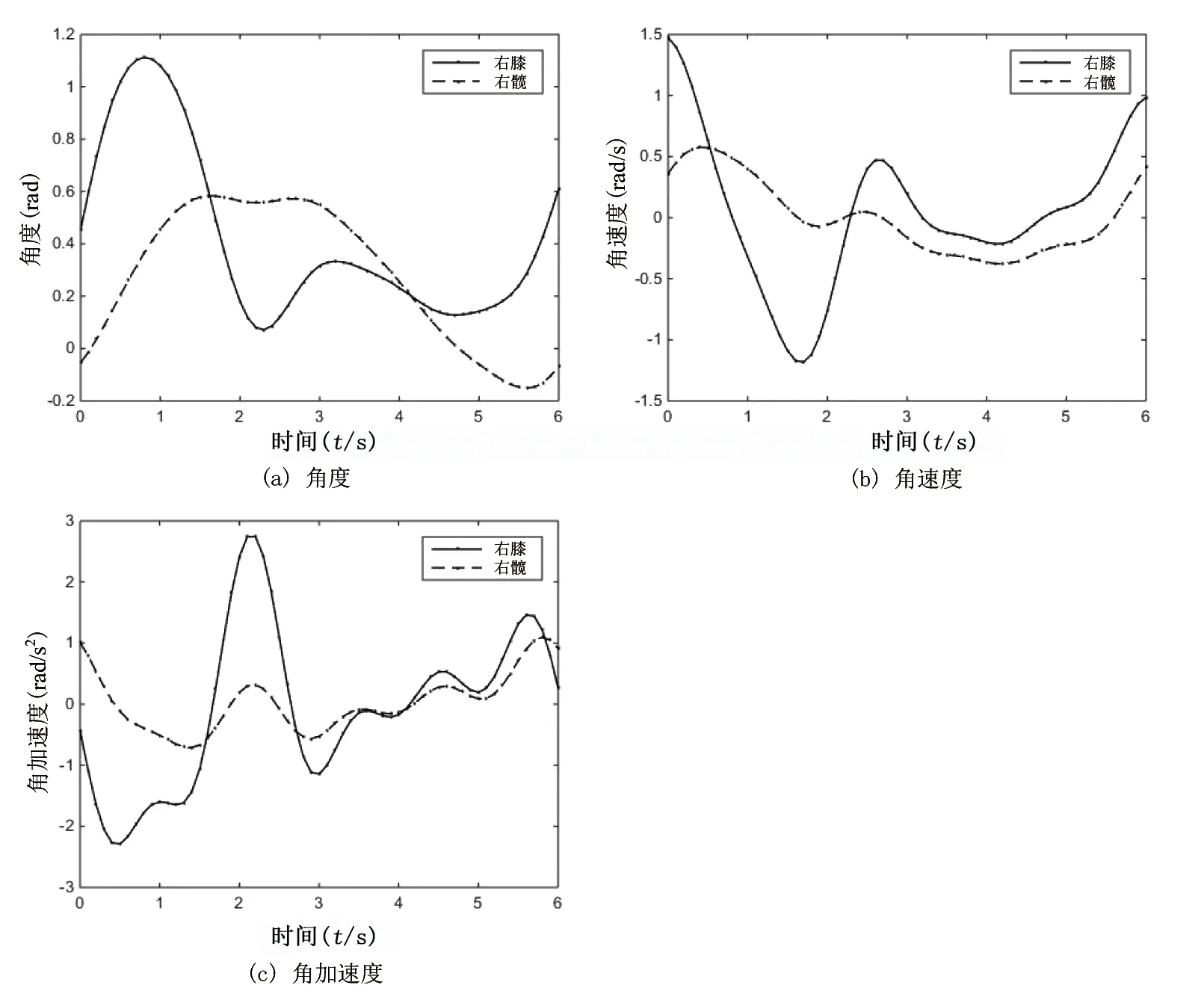
图6 髋、膝关节运动参数

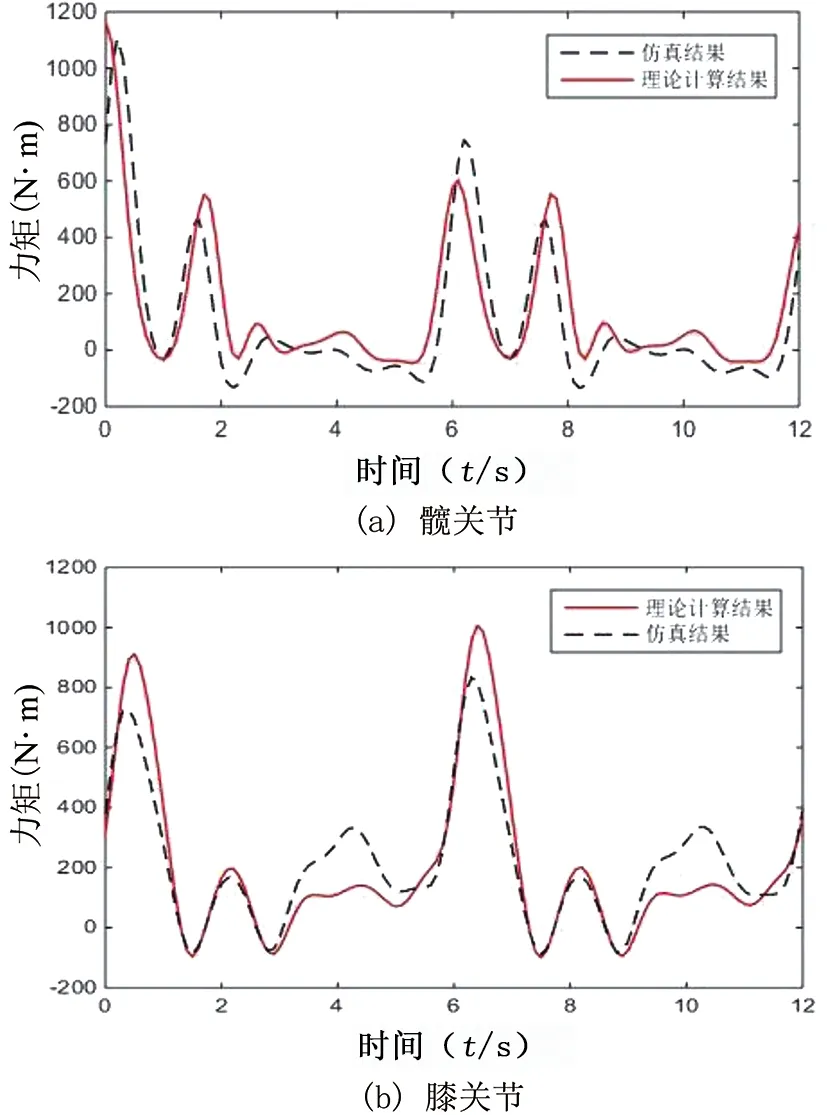
图7 髋、膝关节驱动力矩

经由受试者对试制样机进行穿戴，验证了髋、膝、踝关节各处自由度满足设计要求，大腿、小腿长度调节模块和髋部旋转辅助关节处均与人体下肢运动形成良好配合。

4.2 人体模型样机穿戴测试

为进一步验证下肢外骨骼机器人的稳定性和有效性，实现对规划步态内支撑相和摆动相等良好的复现效果，决定首先采用高还原度人体模型穿戴外骨骼机器人进行样机测试。人体模型(165 cm/43 kg)为等比例还原肢体解剖尺寸，具备髋、膝和踝关节自由度，符合样机模拟穿戴测试实验标准，人体模型穿戴下肢外骨骼机器人测试场景，见图9。

将人体模型绑缚于下肢外骨骼机器人，使人体模型关节轴线与外骨骼机器人关节处轴线相重合，通过操作蓝牙开关手柄，使得人体模型穿戴外骨骼机器人进行规划步态运动，在测试过程中将驱动器端口连接到上位机平台进行图像和数据监测[23]。以右侧主动关节为例，通过上位机获得测试图像见图10。

根据人体模型穿戴下肢外骨骼机器人进行预设步态测试获得的主动关节处图像可以看出，在步态周期中，髋、膝关节的运动轨迹与预设的规划步态轨迹近乎一致，行走过程中步态相位转换平稳，重心稳定，下肢外骨骼机器人的稳定性和有效性得到进一步验证。

图9 人体模型穿戴样机测试

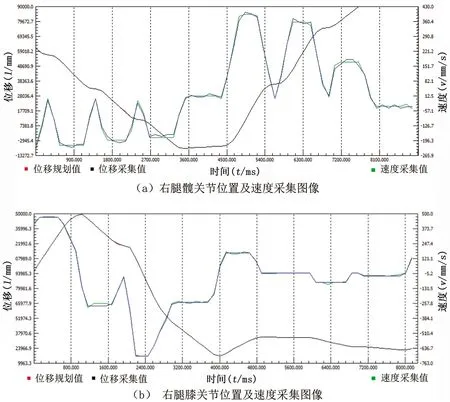
注：左侧坐标轴为位置跟踪图像坐标，右侧为速度跟踪图像坐标。

4.3 人体穿戴步态测试

通过人体模型进行样机穿戴测试，下肢外骨骼机器人的步态稳定性和有效性得到了初步验证。此次人体穿戴步态测试实验招募5名受试者，其中男性3名、女性2名，年龄(23.6±1.5)岁；身高(1.71±0.06)m；体重(58.5±9.5)kg；均为无肌肉和下肢关节疾病的在读大学生。实验设备选用Qualysis高精度三维运动捕捉系统搭配Miqus运动高速红外镜头，人体穿戴测试在Qualysis光学运动捕捉环境下进行[24-25]，见图11。

受试者调整并穿戴下肢外骨骼康复机器人，根据标准下肢运动捕捉贴点方案在外骨骼机器人上粘贴marker点，经由标定杆进行空间坐标系标定[26]，确定系统精度为0.019 mm,采样频率100 Hz。将标准贴点方案下捕捉到的反光marker点进行连接，得到光学捕捉环境下，人体下肢穿戴外骨骼机器人的连杆捕捉结构，见图12。

图11 人体穿戴步态测试

图12 穿戴外骨骼机器人下肢连杆捕捉结构Fig.12 Capture structure of lower limb with wearing LLERR

受试者依次穿戴下肢外骨骼机器人，在拐杖的辅助下，下肢做到不主动发力，由电机驱动外骨骼机器人带动人体下肢在行走测试步道上完成一个周期内的预设步态测试，为了达到更好地模拟和适应截瘫患者使用下肢外骨骼机器人进行康复的场景和效果，结合身体障碍生物力学特征的分析[27]，将一个完整的外骨骼机器人驱动步态周期延长为12 s，并通过各驱动电机间的协调配合，对步态相位进行调整，增加行走时的稳定性，完整的外骨骼机器人下肢运动规律包含支撑相位(约占步态规划的60%)和摆动相位(约占步态规划的40%)，具体的规划步态流程见图13。

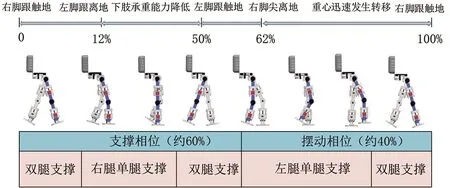
图13 人体穿戴测试步态规划流程Fig.13 Gait planning process for human body wearing LLERR

测试过程中光学运动捕捉镜头记录每位受试者下肢marker点的运动轨迹，通过对一个完整规划步态周期内受试者的人体下肢穿戴外骨骼机器人的连杆捕捉结构进行分析，得出双腿髋、膝关节处运动轨迹见图14。

图14 下肢双侧髋、膝关节运动轨迹

由图14可以看出，外骨骼机器人带动人体下肢进行预设步态行走达到预期效果，外骨骼机器人带动人体下肢运动轨迹与规划步态轨迹近乎一致，分析误差主要来源于运动捕捉过程中存在marker点受到遮挡出现捕捉信号丢失，尽管采用线性插值的方法对丢失数据进行了补偿，但不可避免引进误差。运动轨迹变化符合下肢运动规律，并且对下肢外骨骼康复机器人进行人因工程学分析[28]，从主观角度邀请受试者在完成穿戴测试后填写NASA-TLX主观评价量表，对受试者从体力负荷、努力程度、受挫程度和舒适性等方面进行主观评估[29]，受试者均无明显不适和不良反馈，下肢外骨骼机器人用于人体穿戴步态行走时的稳定性和有效性在主客观角度均得到了验证。

5 结论

本研究从运动学建模、动力学建模、虚拟样机技术仿真、样机试制与穿戴步态测试四个方面，对一款用于辅助下肢运动功能障碍患者的下肢外骨骼康复机器人进行了分析。分别采用D-H法和拉格朗日法对外骨骼机器人单侧下肢进行运动学和动力学建模，通过理论研究得出各运动关节间运动学与动力学关系，并在Adams中进行仿真对比验证，曲线拟合误差均处在合理范围内，验证了理论分析的正确性，为后期运动控制、生物力学特性优化分析等提供了良好的基础。

样机试制及装配穿戴，验证了总体结构设计方案的可行性，选用人体模型进行前期样机规划步态测试，获取速度与位置跟踪图像，进一步验证了外骨骼机器人的稳定性和有效性。招募受试者在光学运动捕捉环境下进行人体穿戴样机步态测试，从主、客观角度验证了外骨骼机器人带动人体下肢进行预设步态行走可达到预期效果。后续需要进一步对生物力学参数变化和控制精度深入探讨，完善人体下肢康复训练步态，为医院脊髓损伤康复患者穿戴预实验做好充分准备。