基于拓扑优化的股骨柄假体生物力学的研究*

张婷婷，程云章

(上海理工大学 上海介入医疗器械工程技术研究中心，上海 200093)

引言

髋关节是人体最大的负重关节，其病变会严重影响患者的生活质量。全髋关节置换术(total hip arthroplasty, THA)利用人工髋关节置换损伤的股骨恢复关节功能，减轻关节疼痛，矫正肢体畸形[1]。人工髋关节由股骨柄、股骨头、衬垫和髋臼杯组成。THA自19世纪出现以来，已成为骨科最成熟的手术之一，但人工假体与自然股骨的弹性模量之间的差距会造成不同程度的应力遮挡现象[2]。THA后，原本由股骨独立承担的髋关节力转为由股骨与假体分担，同时，高弹性模量的假体汇集了更多的载荷，使得载荷传递到股骨路径受阻，从而使股骨的应力分布不同于自然股骨，出现局部的高应力区和低应力区。在高应力区，应力集中可能会造成骨折；在低应力区则会出现不同程度的骨溶解现象[3]。骨在自然生长的情况下，骨组织的形态和密度会随着生物力环境的改变而改变。应力遮挡使得低应力区的股骨无法接受足够的应力刺激而引起骨质丢失。因此，关于假体的材料、固定方式、结构等方面仍有很大改进空间。

拓扑优化是一种在给定区域内生成最佳的形状和材料分布的数学技术[4]，是结构优化的一种，可分为密度法、晶格法、水平集法、无参数变形法等，所有方法均依赖于有限单元法(finite elementmethod, FEM)[5]。基于上游有限元分析系统，通过将区域离散成有限元网格，计算每个单元的材料属性，在给定的响应约束下改变材料分布以优化目标[6-9]。而密度法会根据模型中每个元素的密度执行优化[10]，它使用固体各向同性材料惩罚模型(solid isotropic material with penalization, SIMP)，单元密度不连续，只能是离散的0或1[11]。此方法已经集成到Hyperworks、ANSYS、NASTRAN等多个软件中，并被应用到植入体的优化设计中[12-16]。由于拓扑优化导致的轻量化会带来刚度的降低，为了保证模型刚度，柔度的最小化是拓扑优化中很重要的目标，其物理意义是刚度的反比。2019年，Munteanu等[17]利用软件TruForm作为Solidworks的拓展，对钛合金假体进行了拓扑优化设计，优化假体在满足轻量化15%的情况下，满足了标准ISO 7206/4和ISO 7206/6要求。吴乃超等[18]也在现有髋关节Synergy股骨柄假体的基础上进行拓扑优化，还基于晶格在植入物中的优势，设计了概念性“梯度假体”。虽因计算机算力的限制未完成理想有限元验证，使简化后“梯度假体”的表现不如常规拓扑优化后假体，但仍为后续的设计提供了新的思路。Niroomand等[19]利用ABAQUS的SIMIP算法对假体进行了拓扑优化和简化优化假体的设计，优化后的假体令股骨的力线分布更加均匀，甚至减轻了骨-假体界面的松动。至今为止，关于拓扑优化的研究主要使用质量或体积为约束，尚无研究应力约束下拓扑优化假体力学性能的改变，及其对于后续置入股骨的影响。因此，本研究使用基于密度的拓扑优化方法，以最小化柔度为目标、应力为响应约束对通用股骨假体进行结构优化，探索不同保留阈值下，体积对优化假体力学性能的影响，及优化假体对股骨应力遮挡现象的影响。

1 方法

1.1 通用假体有限元分析

在3-matic中对于假体模型，设置目标三角形边长为1.5 mm，用适应性网格方法画面网格。利用平滑工具，设置平滑因子为0.7。创建四节点四面体单元(Tet4)，设置最大边长为3 mm。最终获得23 934个单元，5 190个节点，最小单元体积为0.0322566 mm2，最大单元体积为2.52616 mm2。在模型顶部创建一个直径为20 mm的圆形印记面，作为前处理载荷的加载面，以cdb格式导出。

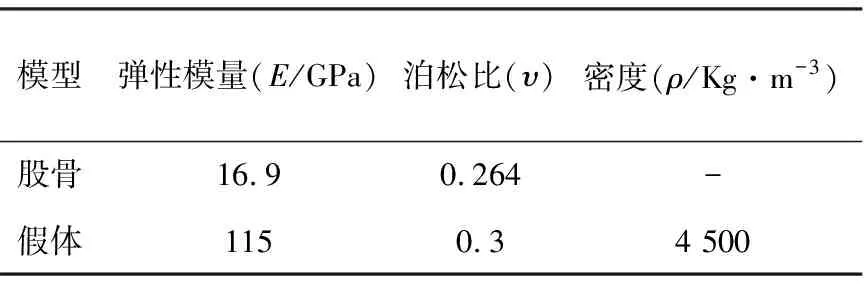
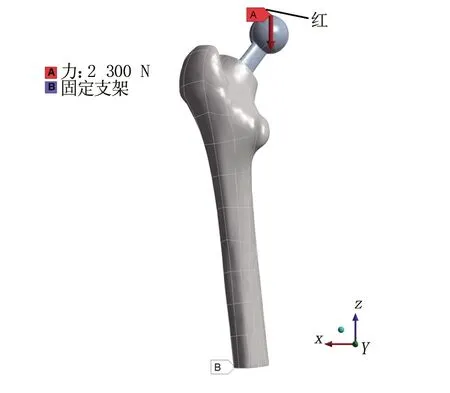
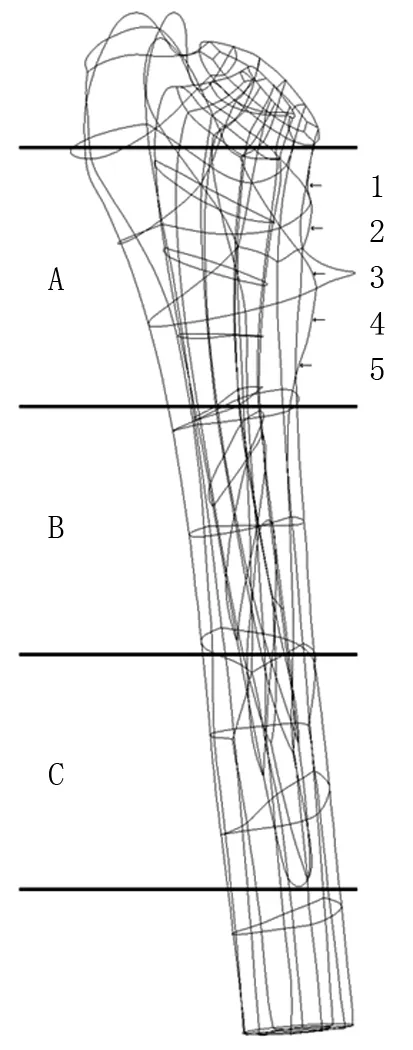
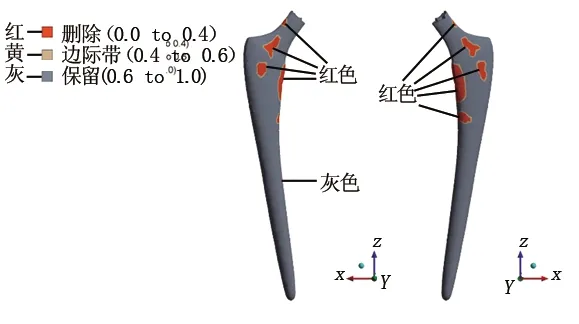
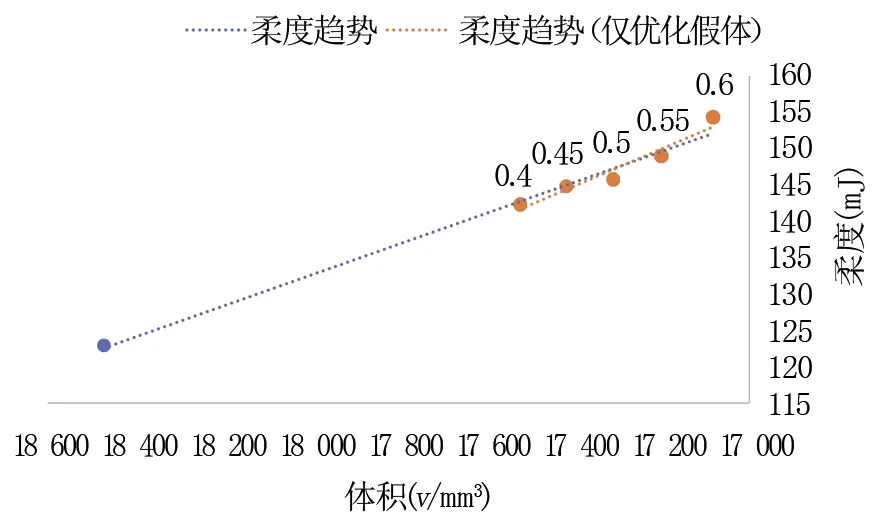
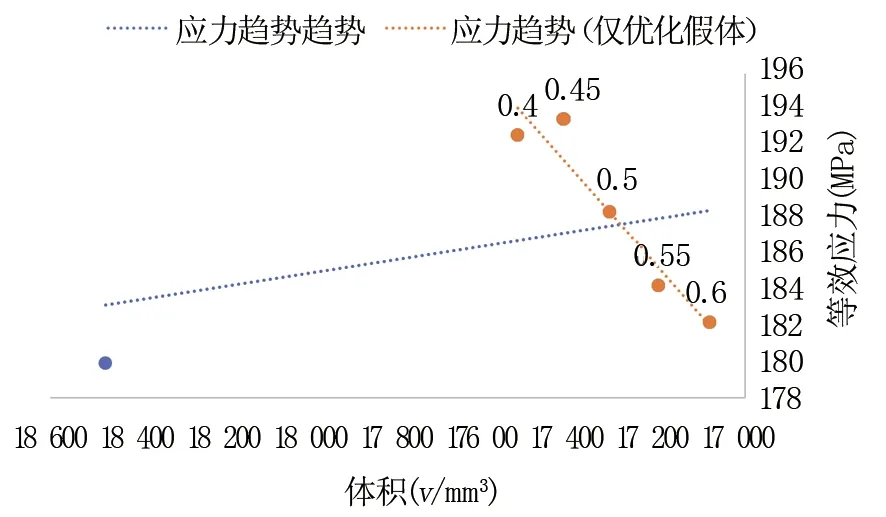
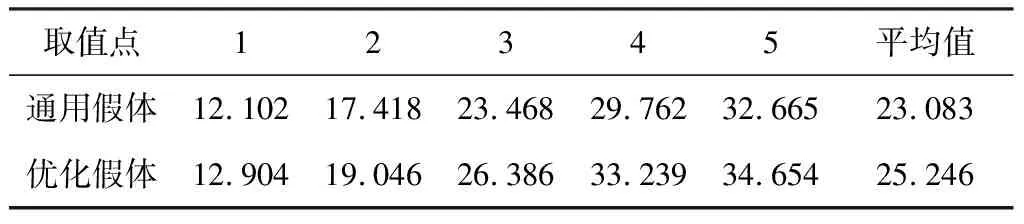
利用ANSYS Workbench 2020 R2中的外部模型模块导入假体模型。关联外部模型模块中的设置栏与静力学模块中的模型栏。在工程数据中创建材料“假体”，设置密度为4 500 kg/m3，弹性模量为55 000 MPa，泊松比为0.33。由于此假体从头部中心到骨柄顶端的距离在120 mm和250 mm之间(120 mm

1.2 拓扑优化

对于本研究所使用的应力约束下的拓扑优化方法，Holmberg与Le等[21-22]做出了突出贡献。在分析设置中，为了保证优化后模型最大程度满足优化设置，最大迭代次数设置为500，最小标准密度为0.000 1，收敛精度为0.05%，惩罚系数为3，选择序列凸规划法(sequential convex programming, SCP)作为解算器。优化区域为除假体头的所有部分,见图2。

目标为最小化柔度。在轻量化假体的需求下，仍要最大限度地保证假体的刚度。响应约束设置为最大冯米塞斯应力99.98 MPa。即假体50%最大等效应力。最后添加制造约束。由于其优化方案的特殊性，拓扑优化解决方案可能会产生在传统制造业中无法制造的设计，而在后期制造过程中，不按预期设计对制造工艺进行任何更改都可能破坏原始设计的完整性，也降低了拓扑优化的意义。因此，本研究根据制造过程添加了制造约束，其应用于拓扑优化系统时，可以通过指定制造限制来帮助减轻设计困难。本研究指定尺寸大小为制造约束，此类型能够制定支撑结构的最小厚度和最终设计中连接部件的最大厚度。虽然后续可能的增材制造已经解决了该问题，制造约束仍然降低了增材制造的难度，且此类型保证了打印体最小尺寸的刚度。

1.3 假体-股骨系统有限元分析

在3-matic中将Implant和Femur模型以Binary stl格式导出，在Geomagic Wrap中进行曲面化，并以Step - AP214格式导出。做相减布尔运算后，把运算后的模型在Geomagic Design中与假体模型合并为一个假体-股骨系统模型。至此完成创立可被ANSYS接受的假体-股骨系统文件。

在ANSYS Workbench中的静力学模块创建分别为股骨和假体的材料，材料参数见表1。

为方便说明，股骨采用简化Gruen分区的方法，并采集其中5个点的数据对其应力进行比较。具体方法为：以股骨距区和假体为边界，平均分为3份，见图4。其中A区是本研究感兴趣的区域。在A区基础上，在股骨距区表皮从上到下平均取5个点的参数，取其平均值作为优化前后股骨的比较应力值。

表1 模型材料参数

设置模型间的接触为无摩擦，边界条件见图3[23]。

图3 假体-股骨系统边界条件

图4 简化Gruen分区及A区取值点

2 结果与讨论

2.1 优化结果

在实验过程中，通过解决方案信息的目标与全局应力响应收敛实时曲线得知，在迭代进行到第20次左右，迭代曲线已趋于平稳，但并未达到设置的收敛标准。因此，在迭代第50次时停止，此时得到的模型视为该设置下的最优模型，得到以下节点平均结果的拓扑密度云图，见图5，最终的平均拓扑密度为0.89978。图中显示了三个色带：红色色带所示的保留阈值为0～0.4，意为删除；黄色色带所示的保留阈值为0.4～0.6，作为边际带，后续可根据需求在此范围内选择合适的保留阈值；灰色色带所示的保留阈值为0.6～1.0，意为保留。保留阈值同时也与杨氏模量相关联，即高保留阈值意味着它能保有高杨氏模量和承受更强的压力。经过拓扑优化得到优化假体的基本构型。可以看出，假体的下半部均为灰色，不能删除；而在颈部形成了5个大小形状不一的块斑，每个块斑由约0.6 mm的边际带围成，将优化区域的保留带与删除带隔离开。

图5 拓扑密度云图

在拓扑密度处添加平滑选项，生成保留阈值分别为0.4、0.45、0.5、0.55、0.6的优化假体stl文件，见表2。导入3-matic进行处理，再导入ANSYS进行分析，步骤与章节2相同。

表2 不同保留阈值下的假体

在Fraldi等[24]的研究中，使用了保留阈值超过0.4～0.6范围的做法。该做法使得不同保留阈值的假体构型有着很大的差异，因此，在后续分析中认为构型对结果产生了更大的影响。本研究由于优化假体皆是在基本构型的边际带中保留阈值，因此，在后续的分析中，认为优化假体体积对结果的影响大于构型对结果的影响。

2.2 有限元分析结果

2.2.1体积与柔度的关系 在SCP中，应变能与柔度有着同样的内含[13]。柔度越小，假体的应变能越小，刚度越强。本研究设置最小化柔度为拓扑优化目标，因此，在结果部分把测得的应变能的值等效于柔度的值。

不同体积对应的柔度见图6。通过对优化前后假体应变能的测量可以看出，优化前假体比所有优化后假体柔度小，为123.06 mJ，优化后假体的柔度皆比优化前假体大，且随着假体体积的减少而增加，由保留阈值为0.4的142.31 mJ增加到保留阈值为0.6的154.28 mJ。柔度趋势的线性拟合为y=-0.0202x+514.16，R2=0.9865。仅优化假体的线性拟合为-0.0255x+588.88，R2=0.9385。从R2值可以看出，体积对柔度的影响比较稳定，即柔度随着假体体积的减小而增加。由几近重合的趋势线可以看出，柔度只与体积有关，材料的减少会导致柔度的增加，而与优化构型无关。

图6 体积对柔度的影响

2.2.2体积与应力的关系 在全约束切线上方10 mm(D=80 mm)以上的区域评估应力(见图1)。以该方式评估应力可避免因刚性固定的影响在感兴趣的区域产生过多的错误应力。

不同体积对应的等效应力，见图7。通过对优化前后假体应力的测量可以看出，优化前假体比所有优化后假体应力小，为179.96 MPa，优化后假体的应力皆比优化前假体大，且随着体积的减少先增加后减少，当保留阈值为0.45时，应力达到最大值193.49 MPa；而当保留阈值为0.6时，应力为优化假体的最小值182.23 MPa。应力趋势线的线性拟合为y=-0.0037x+252.19，R2=0.113。而仅优化假体的线性拟合为y=0.0272x-283.39,R2=0.9147。从优化假体的应力趋势线R2值可以看出，此时体积对应力的影响比较稳定，即应力随着体积的减小而减小。虽然全部假体的应力趋势线显示了一定的趋势，但过小的R2值使得该趋势无意义，因此，不能说应力随着体积的减小而增加。对比优化前后假体应力的变化，观察到拓扑优化得到基本构型后的假体应力都比通用假体大，而体积与应力的关系仅在优化假体中表现稳定，且其趋势与应力随全部假体变化趋势相反。因此，在拓扑优化前后，应力受构型和体积的双重影响，且此构型的影响占据了主导因素。此构型会增加假体的应力，而在此基础构型下，应力有随体积的减小而减小的趋势，能够抵消部分构型带来的影响。

图7 体积对应力的影响

2.2.3优化前后假体对股骨应力的影响 在此方法下，优化后假体刚度下降，且假体体积越小，刚度丢失越严重。因此选择折衷参数，即保留阈值为0.5的假体做后续分析。优化假体的置入方式与通用假体相同。测得置入优化前后假体的股骨A区应力值见表3。

表3 优化前后假体在不同取值点处的应力值(MPa)

宏观来看，轻量化后的假体对比通用假体更有断裂损坏的风险，但随着一定限度内轻量化的加深，此风险得以缓解。虽然此方法整体上造成了假体力学性能的下降，但由优化前后假体对股骨应力的影响中可以看出，刚度下降的优化假体能够一定程度减轻股骨距区的应力遮挡现象。

3 结论

本研究利用股骨柄假体在3-matic中划分网格后导入ANSYS创建材料、边界条件进行分析。以柔度为目标、99.98 MPa应力为响应约束进行拓扑优化，保存保留阈值分别为0.4、0.45、0.5、0.55、0.6的假体，分析不同保留阈值下体积对其力学性能的影响，并筛选出保留阈值为0.5的假体置入股骨，对比置入优化前后假体对于股骨的影响得到以下结论：拓扑优化后的假体基本构型在颈部有5个不规则的孔洞，每个保留阈值下的构型差异不大，在体积上有每0.5保留阈值平均相差109.6 mm3的区别。优化后假体的柔度皆比优化前假体大，且随着假体体积的减少而增加。优化后假体的应力皆比优化前假体大，且随着体积的减少先增加后减少。应力受构型和体积的双重影响，且构型的影响占据了主导因素。比较置入优化前后假体的股骨A区取值点平均应力发现，保留阈值为0.5的优化假体相较于通用假体能减小股骨的应力遮挡。综上所述，假体的轻量化必然会令其损失自身的部分力学性能，但从应力遮蔽产生的原理来看，优化假体上升的柔度才会减轻应力屏蔽现象。如何设计能够平衡假体使股骨的性能达到一个更稳定的状态，以及进一步筛选合适的设定指标，将是后续的研究方向。