MTICA-AEO-SVR股票价格预测模型

邓佳丽，赵凤群，王小侠

西安理工大学 理学院，西安 710054

股票作为经济市场的重要组成部分，一直受到政府和投资者的关注。股票价格的准确预测可以引导市场平稳运行，也能使投资者最大限度地规避风险，做出正确的投资策略，从而获得最大收益。然而，由于股票市场的随机性、非平稳性和不确定性，使得股价预测成为一项具有挑战性的工作。依据统计学理论，时间序列分析方法常被用于股票价格的预测[1-2]。但时间序列分析方法是建立在一系列假设条件之上的，例如数据的独立性和依赖性、数据的分布以及各种参数的有效范围等，而实际中满足这些假设条件是困难的，这使得该方法的实用性不强。支持向量机回归（support vector regression，SVR）[3]是基于统计学习理论和结构风险最小化原理的优化模型，其结构简单，泛化能力强，近年来被广泛应用于金融时间序列预测中。Xiao等人[4]基于奇异谱分析（singular spectrum analysis，SSA）和SVR建立了股价预测模型；Aggarwal等人[5]提出一种完全经验模态分解和SVR比特币预测模型，并证明了该模型的有效性。但采用凑试法或网格搜索法对SVR的惩罚系数和核函数参数寻优效率较低，因此，有研究者将智能优化算法引入到SVR中，以提高模型的预测效率。Lahmiri[6]利用粒子群算法（particle swarm optimization，PSO）优化SVR参数提高了SVR的预测性能；Liu等人[7]采用灰狼算法（grey wolf optimizer，GWO）对SVR模型参数进行优化建立选股模型，然而PSO、GWO存在收敛速度慢和易陷入局部极值的缺点。

由于股票价格序列具有高噪声的特点，在价格预测前往往需要做去噪处理。独立分量分析（independent component analysis，ICA）[8]是一种从混合信号中分离出独立分量的特征提取方法，也常被用于数据的去噪。王灿锋和孙曜[9]提出了一种改进独立分量分析自动去除眼电伪迹的方法，该方法有效降低了去伪迹耗时，极大提高了信噪比；Sueaseenak[10]采用ICA算法对心电信号进行了去噪处理进而提高了心电信号的相关系数和信噪比；Lu[11]提出了一种基于ICA的神经网络去噪方法并用于股票价格预测。Fast ICA算法是ICA模型中最简单的一种，其具有收敛速度快、形式简单等优点，但是对分离矩阵的初始值敏感，鲁棒性较低。为了解决这一问题，Chao等人[12]采用Huber M-估计作为Fast ICA的非线性函数；Meng等人[13]对Huber M-估计进行改进；Jianwei等人[14]将Tukey M-估计作为复值Fast ICA的非线性函数，提高了算法的稳定性。

为了进一步提高Fast ICA算法的鲁棒性，并获得较好的分离效率，在Tukey M估计的基础上，构造了一种新的非线性函数，提出了MTICA算法；在股票价格预测中将人工生态系统优化算法[15]（artificial ecosystem optimization，AEO）应用于SVR参数的调优，以克服SVR收敛速度慢和易陷入局部最优的缺点，增强预测性能，由此建立了MTICA-AEO-SVR股票价格预测模型。

1 Fast ICA简述

ICA是指从混合信号中分离源信号的统计方法，其数学模型为：

其中，x(t)=[x1(t),x2(t),…,xn(t)]T表示已知的n维观测信号，s(t)=[s1(t),s2(t),…,sm(t)]T表示m维源信号，A为未知的n×m维混合矩阵，v(t)为高斯噪声。ICA算法的目的是在源信号s(t)和混合矩阵A都未知的条件下，仅通过已知的观测信号x(t)来获得分离矩阵W，使得：

尽可能地逼近源信号s(t)。

Fast ICA是一种简单直观的ICA模型，以极大化非高斯性作为统计独立性判据，将负熵作为非高斯性度量，运用牛顿迭代法进行优化。负熵J(y)被定义为：

其中，ygauss表示与y具有相同方差的高斯随机变量，H(·)表示熵运算。由于在相同方差的随机变量中，高斯变量的熵最大，所以，J(y)≥0。当且仅当y服从高斯分布时，J(y)=0。

为了简化计算，Hyvarinen基于最大熵原理给出了一种负熵的近似公式：

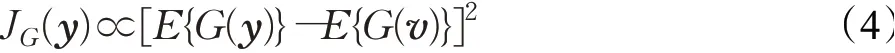
其中，G(·)表示非线性函数，E(·)表示均值运算，v表示均值为0，方差为1的高斯变量。

在Fast ICA算法中，非线性函数的选取对于其分离性能和效率有着较大的影响，通常来说，非线性函数G(y)的选择标准有：

（1）统计特性E(G(y))不难求得。

（2）G(y)的影响函数，即其一阶导函数G′(y)有界。

（3）当y逐渐增大时，非线性函数G(y)的增长速度不能快于y2，即。经典的非线性函数有：

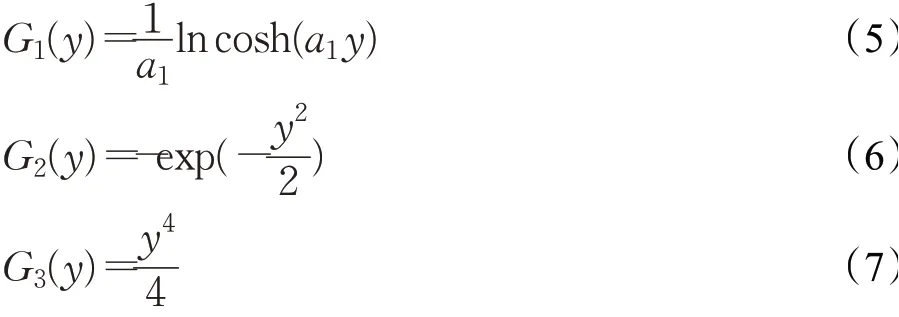
式（5）中，常数a1的取值范围为[1，2]，通常取a1=1。但是，使用这三种经典非线性函数时，数据中的野点对估计效果影响较大，估计结果不够稳健。因此，本文尝试寻找新的非线性函数G(y)以提高鲁棒性。

2 MTICA算法

2.1 非线性函数的构造

在传统Fast ICA算法的目标函数中，使用了一个单一的非线性函数，这使得目标函数对异常值的控制不佳。本文构造了一个如式（8）所示的非线性分段函数G(y)来计算式（4），构成新的算法，不妨称为MTICA算法。

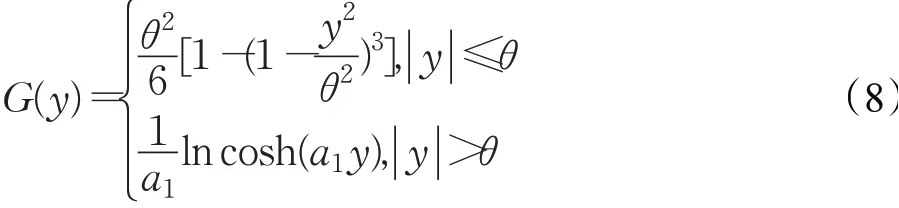
其中，参数θ表示阈值，该函数的一阶导函数G′(y)和二阶导函数G″(y)如下所示：

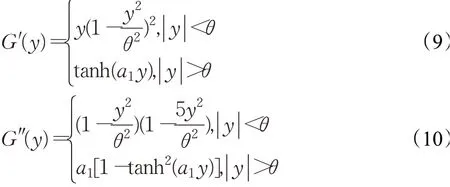
根据非线性函数的选择标准，从式（8）可以看出，当|y|≤θ时，非线性函数只涉及最基本的四则运算和平方运算。当|y|＞θ时，为式（5）所示的经典非线性函数。因此，统计特性E{G(y)}不难求得。另外，当|y|＜θ时，有时，有tanh(a1y)≤1,影响函数G′(y)有界。当|y|＞θ时，有G(y)的增长速度小于y2。因此，所构造的G(y)满足ICA算法的要求。但构造的G(y)在小于阈值点的部分，相比经典非线性函数增长速度更慢，且形式简单。在大于阈值点的部分，采用对数非线性函数可以进一步平滑阈值点的急剧过渡，进而减小异常值对ICA分离性能的影响，所以具有鲁棒性更好的优势。根据大量实验验证，当常数a1=2/(3π)，θ=6时，分离效果最佳。

2.2 分离性能测试

2.2.1评价指标

采用相关系数和信噪比来评价算法的分离效果。相关系数的定义为：

信噪比的定义为：

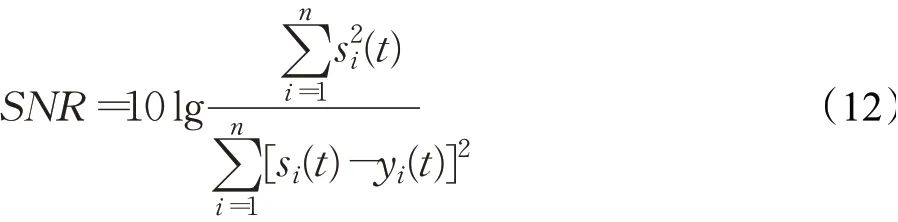
其中，s表示源信号，y表示分离后的信号，cov(·)表示协方差。

2.2.2分离结果与分析

以正弦波、锯齿波、方波、随机波为源信号来检验分离算法，源信号的波形图如图1所示。对源信号进行随机混合得到如图2所示的混合信号。

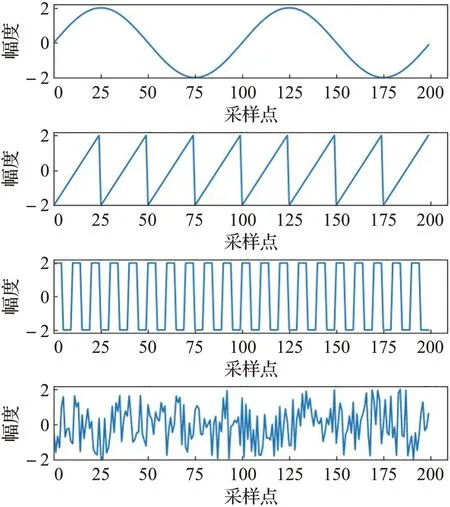
图1 源信号波形图Fig.1 Waveform of source signal

图2 混合信号波形图Fig.2 Waveform of mixed signal

分别用Fast ICA算法、Tukey Fast ICA算法以及MTICA算法对混合信号进行1 000次分离实验，并分别计算了三种算法相关系数和信噪比的均值和标准差。表1是相关系数的均值和标准差。表2是信噪比的均值和标准差。

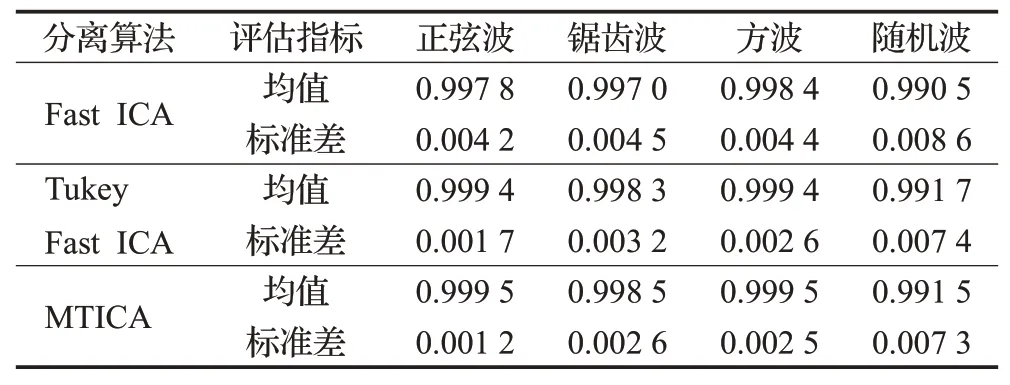
表1 三种算法相关系数的均值与标准差Table 1 Mean and standard deviation of correlation coefficient of three algorithms

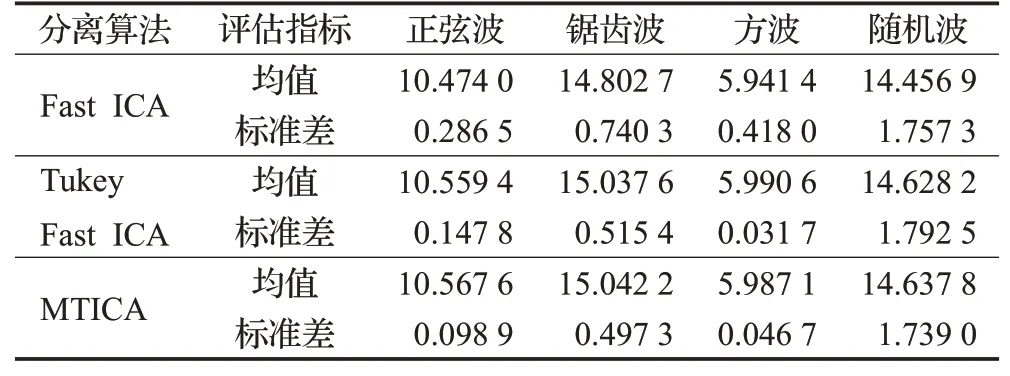
表2 三种算法信噪比的均值与标准差Table 2 Mean and standard deviation of SNR of three algorithms dB

从表1中可以看出，MTICA算法除了随机波的相关系数均值略小于Tukey Fast ICA算法外，其余相关系数均值都大于Tukey Fast ICA和传统Fast ICA，且所有的相关系数标准差都小于Tukey Fast ICA和传统Fast ICA。说明MTICA算法在保持分离精度的情况下，鲁棒性更好。从表2可以看出，MTICA算法除了方波的分离效果微逊色外，其余三种信号分离的信噪比均优于另外两个算法。

Fast ICA算法、Tukey Fast ICA算法和MTICA算法的分离结果分别如图3、图4和图5所示。从图中可以看出，三种算法对于方波和随机波的分离效果相当，均比较彻底；而对于正弦波和锯齿波，MTICA算法的分离结果明显优于Fast ICA算法和Tukey Fast ICA算法。

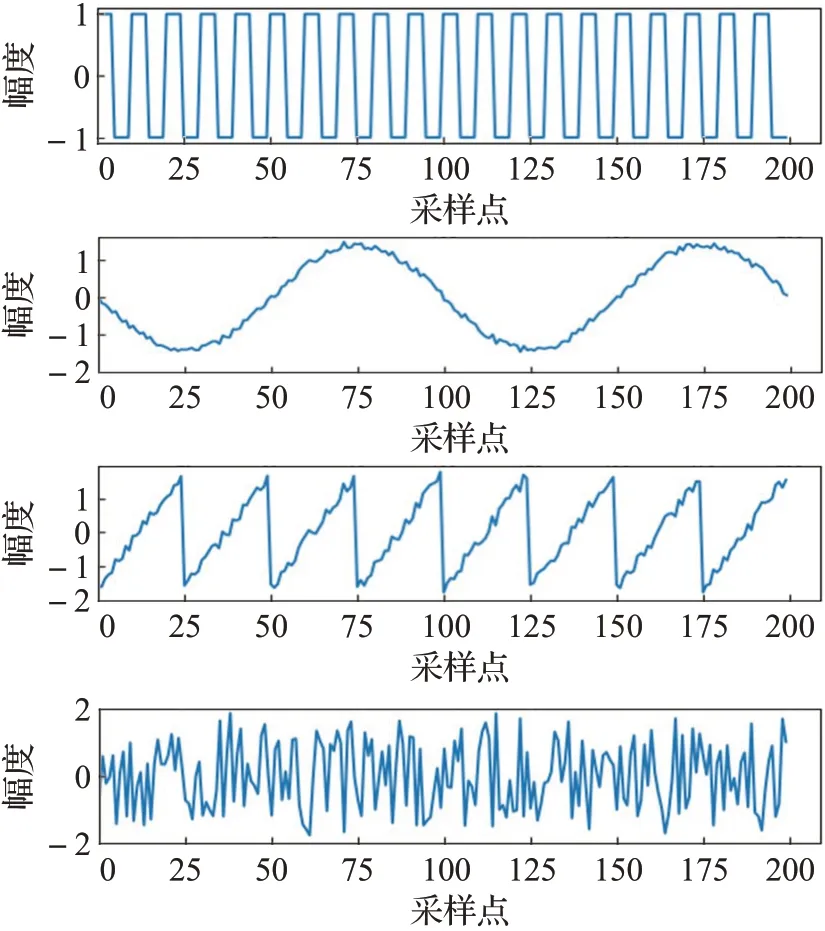
图3 Fast ICA算法的分离结果Fig.3 Separation results of Fast ICA

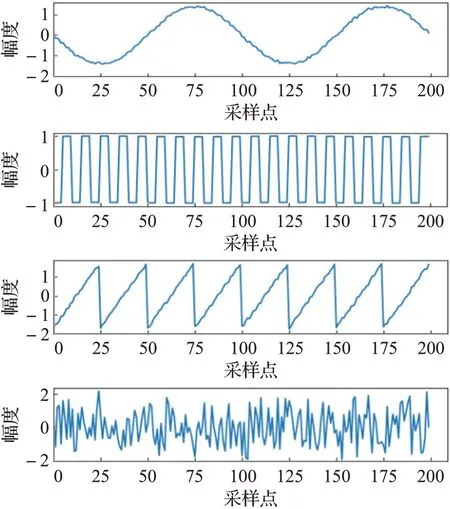
图4 Tukey Fast ICA算法的分离结果Fig.4 Separation results of Tukey Fast ICA

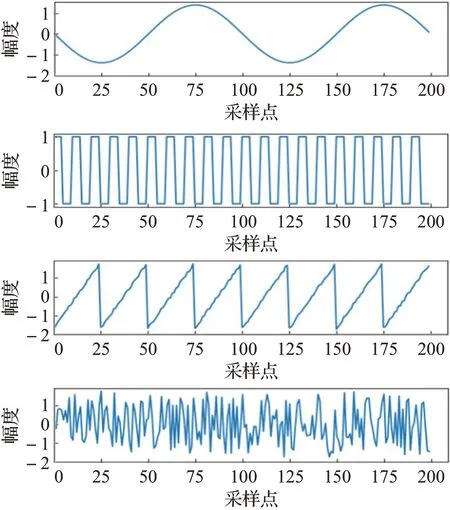
图5 MTICA算法的分离结果Fig.5 Separation results of MTICA

表3给出了三种算法的运行时间，可以看出，MTICA算法的运行时间远低于Fast ICA算法，与Tukey Fast ICA算法的运行时间相当，综合三种算法的分离效果，说明该算法在信号分离时更高效。

表3 三种算法的运行时间Table 3 Running time of three algorithms

3 MTICA-AEO-SVR股票价格预测

由于SVR模型的参数对预测精度有着决定性影响，采用AEO算法对SVR模型中的惩罚系数和核函数参数进行优化，以提高模型的预测精度和预测效率。以此建立的模型称为MTICA-AEO-SVR股票价格预测模型。

3.1 基于AEO算法的SVR模型参数优化

对于一组给定的股票价格历史数据{(x1,y1),(x2,y2),…,(xn,yn)}，其中，x i∈R表示第i个特征向量，yi∈R表示第i个输出，SVR的优化模型为：

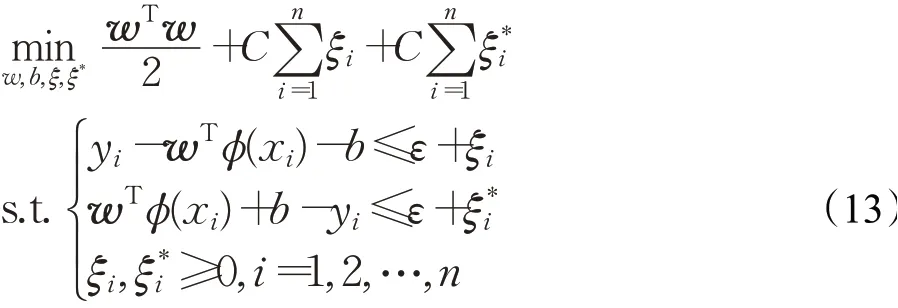
其中，C为惩罚系数，φ(x)为核函数。常见的核函数有：

（1）线性核函数

（2）多项式核函数

（3）径向基核函数

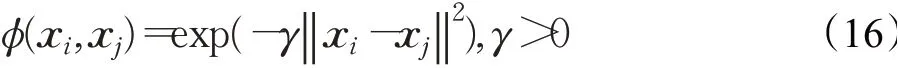
（4）sigmoid核函数

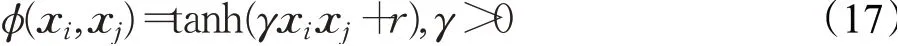
在SVR预测模型中，惩罚系数C、核函数参数γ、损失函数参数ε是影响模型精度的主要参数。其中，惩罚系数C是平衡支持向量的复杂度和误分类率之间关系的。C过大时，会导致模型过拟合；C过小时，会导致模型欠拟合。核函数参数γ影响学习样本在空间分布的复杂程度。γ过大，模型的预测精度较低；γ过小，模型的复杂度过高。损失函数参数ε决定支持向量的个数。ε越大，支持向量的个数越少；ε越小，支持向量的个数越多。另外，r为核函数的常数项，对于多项式核函数和sigmoid核函数有效。因此，选取合适的参数组合，对于预测模型的精度以及复杂度都是关键的。

AEO算法是基于生态系统能量流动的智能优化算法，有着很强的全局优化搜索能力。在AEO算法中，每个个体的能量水平通过适应度值进行评估，且适应度值按降序排列。选择SVR拟合值的均方误差作为适应度函数，AEO-SVR优化模型的目标函数为：

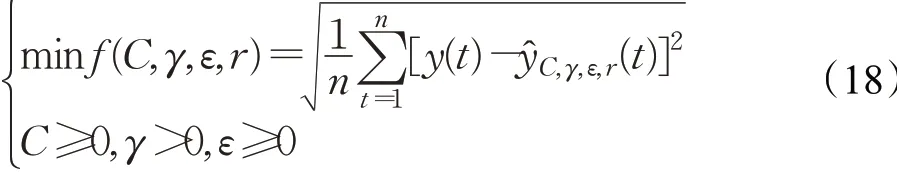
式（18）中，y(t)表示实际值，y^C,γ,ε,r(t)表示拟合值。

设参数向量X={C,γ,ε,r}，通过AEO算法求解优化问题（18），具体步骤为：

步骤1设定参数向量X的寻优范围，AEO算法的种群规模n，最大迭代次数T。

步骤2初始化SVR的模型参数X={C,γ,ε,r}，求解式（13）得到y^C,γ,ε,r(t)，代入式（18）求解优化问题得到当前最佳参数位置Xbest。

步骤3利用式（19）更新生产者位置：

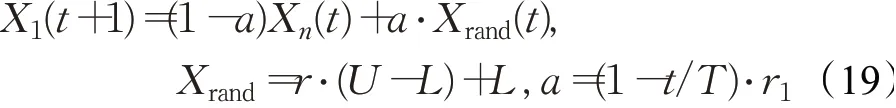
步骤4生成随机数r∈[0,1]，若r＜1/3，利用式（20）更新参数位置；若1/3≤r≤2/3，利用式（21）更新参数位置；其他情况时，利用式（22）更新；计算每个参数的目标函数，并且保留当前最佳参数位置Xbest：

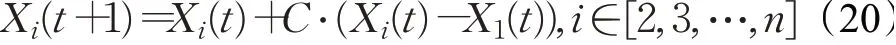
其中：

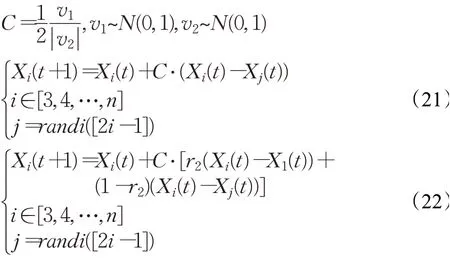
步骤5利用式（23）更新分解过程中每个参数的位置，计算每个参数的目标函数，并且保留当前最佳参数位置Xbest：

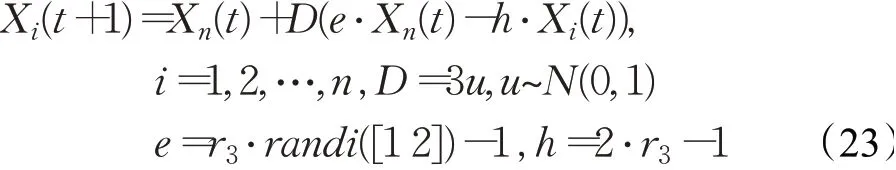
步骤6令t=t+1，判断算法是否达到终止条件，若是，输出全局最优解，算法结束，否则重复步骤（3）至（5）。

步骤7输出式（18）的最优值及全局最优参数Xbest，将最优参数Xbest代入式（13）进行预测。

3.2 MTICA-AEO-SVR预测模型算法步骤

MTICA-AEO-SVR预测模型的算法步骤如下：

（1）选取预测数据样本，并合理划分训练集和测试集，用嵌入法[4]将一维股票日收盘价映射为多维的。

（2）运用MTICA算法对多维股票数据进行分解，得到多个独立分量。采用TnA[16]方法进行排序去噪。

（3）对去噪后的每个分量进行SVR预测，在预测过程中选择合适的核函数，运用AEO算法优化核函数参数，以得到各分量的预测值。

（4）将各分量的预测值作为SVR的输入，以下一日的真实日收盘价作为输出，选择合适的核函数进行预测，获得收盘价预测值。

4 实证研究

4.1 数据准备和预测评价指标

选取上证B股指数（证券代码为999997）2019年9月3日至2021年4月28日的日收盘价数据作为实证研究对象，共包含400天的交易数据。数据来源于通达信金融终端。使用前70%的数据作为训练集，后30%的数据作为测试集。

评价指标为均方误差（MSE）和判决系数（R2）。均方误差用来检验模型的预测精度，判决系数用来评估模型的拟合程度。

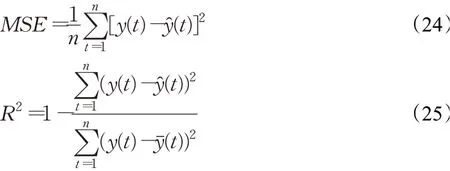
其中，y(t)表示真实值，y^(t)表示预测值，yˉ(t)表示真实值的平均值，n表示测试数据集的长度。MSE值越接近0表明模型预测精度越高，R2越接近1表明模型拟合程度越好。

4.2 实验结果与分析

为消除股票数据高噪声对预测效果的影响，在运用MTICA算法分解后，接着对四个独立分量采用TnA算法进行排序去噪。表4为四个独立分量排序的TnA方法每次迭代的相对Hamming距离（RHD）重构误差。

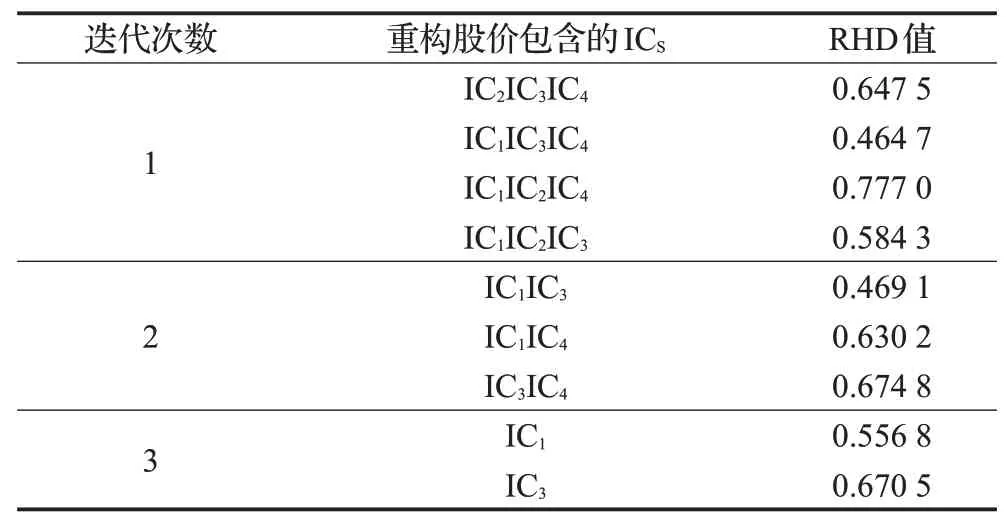
表4 ICS的RHD重构误差Table 4 RHD reconstruction errors of ICS

从表4可以看出，四个独立分量包含有效信息的顺序为IC1＞IC3＞IC4＞IC2。故IC1包含了股票价格的主要信息，IC2含更多的噪声信息。为了减少噪声对预测精度的影响，在后续的预测过程中去掉噪声分量IC2。

根据3.2节所示的步骤，对IC1、IC3、IC4分别做SVR预测，将常见的线性核函数、径向基核函数、多项式核函数，sigmoid核函数分别应用于SVR预测，筛选最优核函数。表5为IC1的预测结果，比较MSE、R2，可以看出基于sigmoid核函数的SVR预测模型最佳，采用AEO算法进行参数优化得到C=0.280,ε=0.021,γ=0.019,r=0.143。IC1预测曲线如图6所示。可以看出，IC1的预测曲线与真实曲线吻合，曲线走势基本一致。根据表4的排序结果可以看出，IC1为主要分量，表示股票价格的长期趋势，波动较为缓慢，因此预测的准确度高。

表5 IC1的预测结果Table 5 Prediction results of IC1

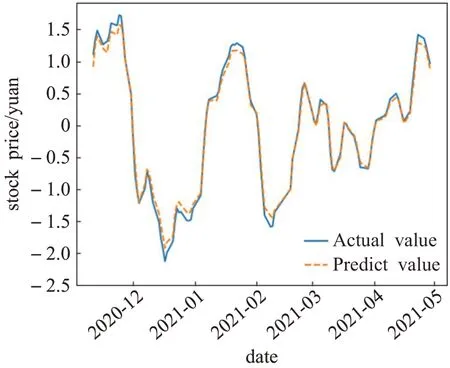
图6 IC1真实值与预测值比较Fig.6 Actual and predictive values of IC1

表6为IC3的预测结果，比较MSE、R2，可以看出基于线性核函数的SVR预测模型最佳，C=0.224,ε=0.096。IC3预测曲线如图7所示。可以看出，IC3的变化较剧烈，预测结果吻合度不如IC1，但走势基本一致，结合表4排序结果，说明IC3包含着股价的细节特征信息。

表6 IC3的预测结果Table 6 Prediction results of IC3

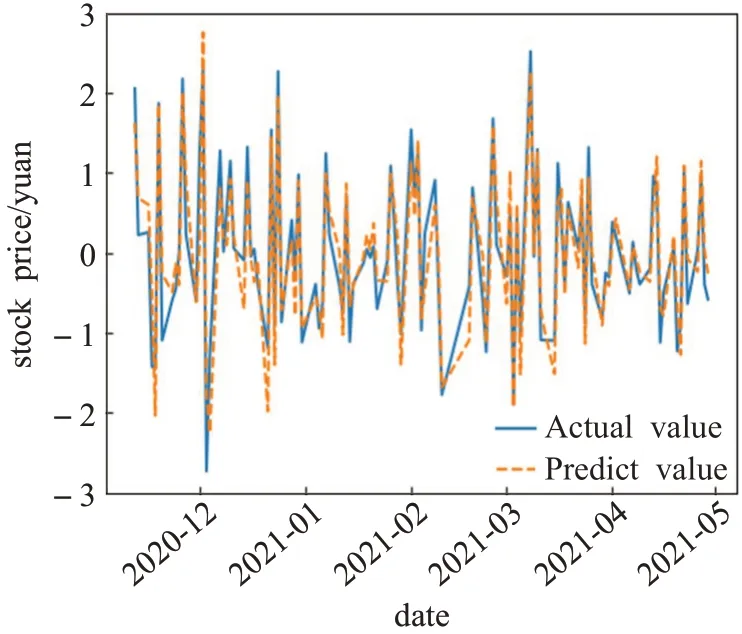
图7 IC3真实值与预测值比较Fig.7 Actual and predictive values of IC3

表7为IC4的预测结果，比较MSE、R2，可以看出基于径向基核函数的SVR预测模型最佳，C=0.650,ε=0.187,γ=0.557。IC4预测曲线如图8所示。可以看出，IC4在个别峰值的预测效果不理想，但曲线走势基本一致，结合表4的排序结果分析出IC4包含相对较少的股价特征信息，且波动变化较大，因此，对该分量的预测是相对困难的。

表7 IC4的预测结果Table 7 Prediction results of IC4

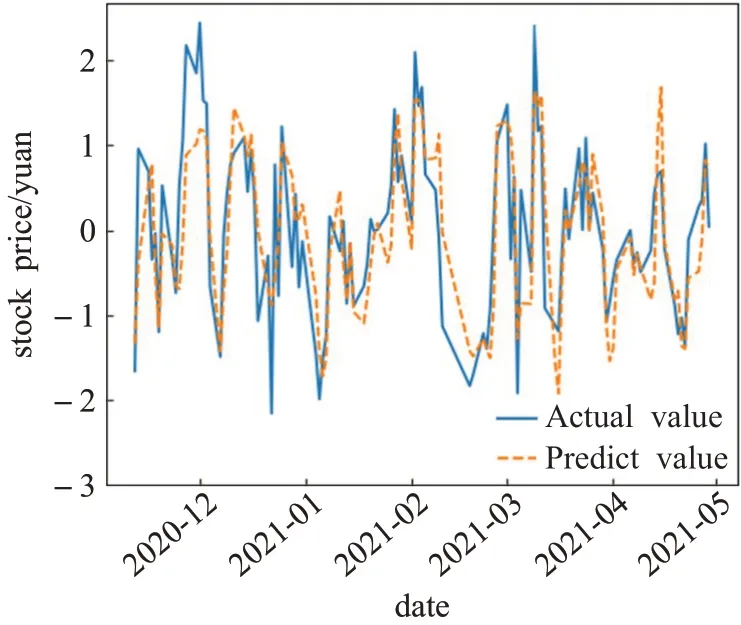
图8 IC4真实值与预测值比较Fig.8 Actual and predictive values of IC4

表8 原股票收盘价的预测结果Table 8 Prediction results of original stock price

分别使用ICA-SVR模型，ICA-AEO-SVR模型和MTICA-AEO-SVR模型对股票收盘价进行了预测。三种模型的预测值如图9所示。其中，图（b）为图（a）中预测部分放大后的效果展示。可明显看出整体上MTICAAEO-SVR模型的预测曲线与真实值曲线更接近；从图（b）标记的细节上可以发现，MTICA-AEO-SVR模型的预测结果成功捕捉到了股票价格的局部突变，而其余两种模型的预测值没有捕捉到该细节变化，说明MTICAAEO-SVR模型无论从长期趋势还是短期预测效果均比另外两种模型准确。表9为三种模型分别预测的MSE、R2和运行时间比较。可以看出，MTICA-AEO-SVR模型较其他两种模型MSE最小，R2最大，从客观上说明MTICAAEO-SVR模型预测结果最优，与图9分析结果一致。另外，MTICA-AEO-SVR模型的运行时间远小于ICAAEO-SVR模型和ICA-SVR模型。因此，MTICA-AEOSVR模型是一种准确高效的股票预测模型。

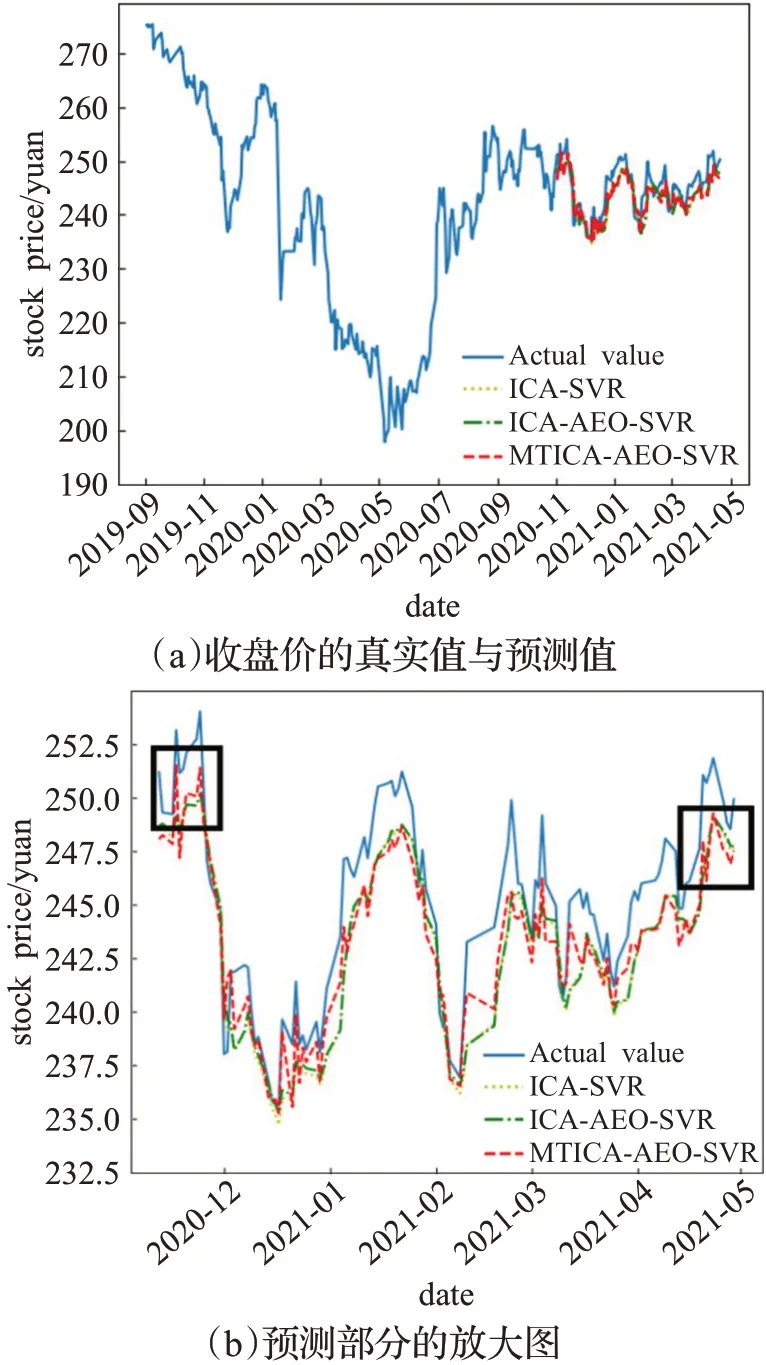
图9 股票收盘价真实值与预测值Fig.9 Actual and predictive values of closing price

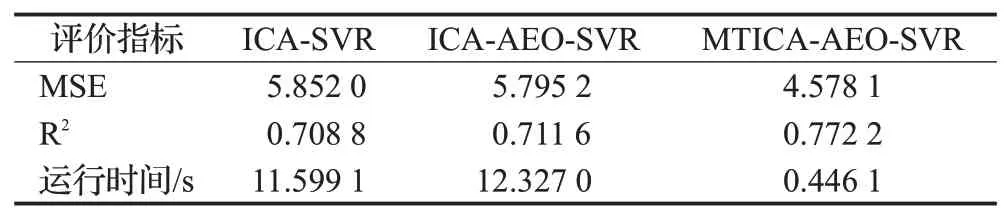
表9 不同模型的预测结果比较Table 9 Prediction results of different models

5 结束语

本文将Tukey M-估计函数与对数非线性函数相结合构造了一种新的非线性函数，克服了Fast ICA鲁棒性不足的缺点。通过实验分析表明，MTICA算法相较于传统的Fast ICA算法和Tukey Fast ICA算法运行时间更短，且鲁棒性更高。针对股票市场固有的复杂性，将MTICA算法与AEO-SVR预测模型相结合，提出了一种新的MTICA-AEO-SVR股价预测模型，实验结果表明该模型是一种高效准确的股价预测模型。