基于邻域拓展的静态路径规划A*算法研究

郭晓静，杨卓橙

中国民航大学 电子信息与自动化学院，天津 300300

路径规划指的是在障碍物空间中，快速有效地寻找出一条从起始位置到目标位置的无碰撞的路径[1-2]。现在广泛使用的路径规划算法有基于概率采样的RRT算法[3]等，它能够快速地在障碍空间中搜索出一条路径，但当环境中的通路狭窄时，算法搜索容易陷入长时间的停滞状态；文献[4]将道路约束加入到RRT算法中限制算法的随机性，以求出符合车辆实际使用的路径，但是它不适用于动态环境下的路径规划；基于图搜索的Dijkstra算法[5-6]是经典的用于解决最短路径问题的算法，但是其搜索过程会耗费大量时间和存储空间；文献[7]对Dijkstra算法的存储结构进行了优化，整体降低了算法搜索的时间复杂度，但是在大地图中其时间花费仍然高于其他算法；文献[8]考虑实际路径中存在的必经点限制，并将其加入Dijkstra算法，虽然能获得满足要求的路径，但是也增加了时间花费；具有启发式思想的A*算法[9-10]被认为是静态环境中进行最短路径规划的最有效方法，但它规划出的路径存在拐角过大、遍历节点较多等缺点；文献[11]将A*算法应用于机器人路径规划问题，传统方法中，机器人只能向8个方向扩展，由于搜索的节点数目较少，在前期就将更优秀的节点从搜索列表中删除，将8邻域拓展至24邻域搜索，提高了路径搜索的自由度，并与动态窗口法结合，提高了路径的平滑度与安全性，但是其在大地图中计算效率低下；文献[12]将搜索节点的多辈父节点信息引入启发函数，以此减少估计代价的局部最优情况，同时融合模拟退火算法优化节点选择，但是其在大地图和障碍物复杂的情况下算法将产生很多无用的节点扩展，进而消耗大量时间；文献[13]针对未知环境中的智能体路径规划问题，提出一种多层双向A*算法，使智能体可以响应环境中的突发障碍，但该方法搜索自由度较低，会使规划出的路径出现绕远的情况；文献[14]针对传统A*算法规划出的路径碰撞威胁大，不适合智能小车实际使用的问题，将障碍物安全距离引入启发式函数，从而降低碰撞威胁，但是该方法会使算法搜索更多的节点。

因此本文针对静态网络路径规划问题，提出一种改进的A*算法，利用A*取评估函数最小节点拓展的性质，生成对应方向向量对额外邻域的拓展进行引导，使传统A*算法有更高的自由度，同时也避免大量增加计算量。然后对获得的路径节点进行检查，进一步剔除冗余节点，使最终所得路径更短、更平滑。将该方法用于大地图环境的路径规划中时，获得的路径比8邻域及24邻域的A*算法更短，搜索时间花费更少。

1 改进的A＊算法

传统A*算法是一种启发式的图搜索算法[15-16]。它依靠评估函数f(n)来引导它的搜索方向。评估函数含有距离函数g(n)和启发式函数h(n)两部分，如式（1）所示：

其中，f(n)是评估函数，表示的是从当前节点n节点到目标点的总路径长度；g(n)是距离函数，表示的是初始节点到当前节点n的实际最短路径长度；h(n)为启发函数，则表示当前节点n到目标点的预估路径长度。

传统A*算法通常选取评估函数值最小的点作为下一步计算节点，以优化搜索路径[17]。即从初始节点开始，计算周围节点的评估函数，选取其中值最小的一个节点作为当前最优节点进行拓展，直到搜索到目标点，然后由目标点回溯到起始点形成一条全局规划轨迹。但是由于A*算法本身的特点，其搜索的自由度不足，进而会使得搜索出的路径不够平滑。

1.1 A＊算法的邻域拓展

传统的A*算法一般采用8邻域搜索，即每个方向都有45°的夹角，这种方式限制了路径的规划形式，容易使最终规划出的路径转折点过多，轨迹不够平滑。

因此本文先将A*算法的搜索拓展至24邻域的形式，如图1所示，在原先8方向的基础上加入额外的16个邻域，形成了1～16个搜索的方向，搜索方向角度从原先的45°夹角变为22.5°，增加了搜索的自由度，从而使得路径更加平滑。该方法适用于静态网络路径规划问题。

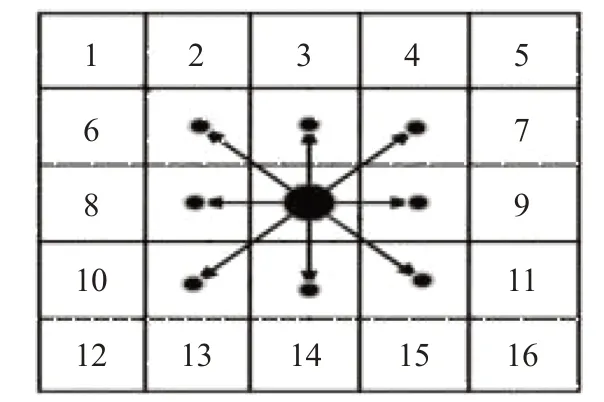
图1 A*算法的24邻域拓展Fig.1 24-neighborhood searching of A*

1.2 确定引导向量优化邻域数量

将A*算法的8邻域搜索拓展到24邻域，增加了搜索时间花费。为此提出引导向量概念，对邻域的拓展方向进行引导，在引导方向上计算额外的拓展邻域，如图2所示。因此，搜索算法不再需要计算24个邻域，也能保证搜索时增加自由度。

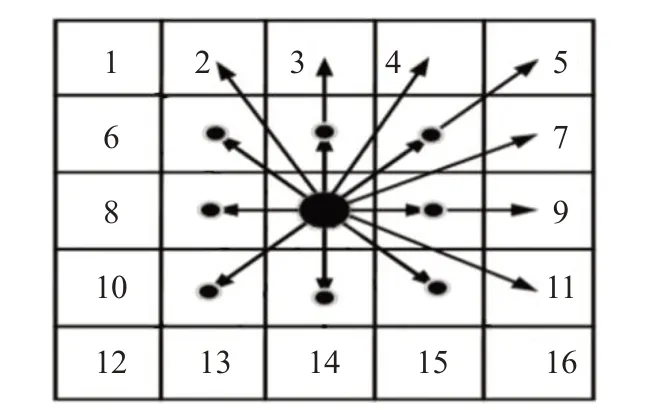
图2 引导A*算法的邻域拓展Fig.2 Searching neighborhood modified by guided vector

定义节点(n.x,n.y)为当前的评估函数值最小节点，节点(pre.x,pre.y)为最近一次评估函数值最小节点，利用它们生成引导向量(Dx,Dy)，如式（2）所示。根据Dx与Dy值的正负，可以将搜索方向分为表1所示的8类。当Dx为负Dy为正时，改进A*算法在传统A*算法的8邻域基础上额外搜索{2、3、4、5、7、9、11}号邻域；当Dx为零Dy为正时，改进A*算法在传统A*算法8邻域的基础上额外搜索{4、5、7、9、11、15、16}号邻域。

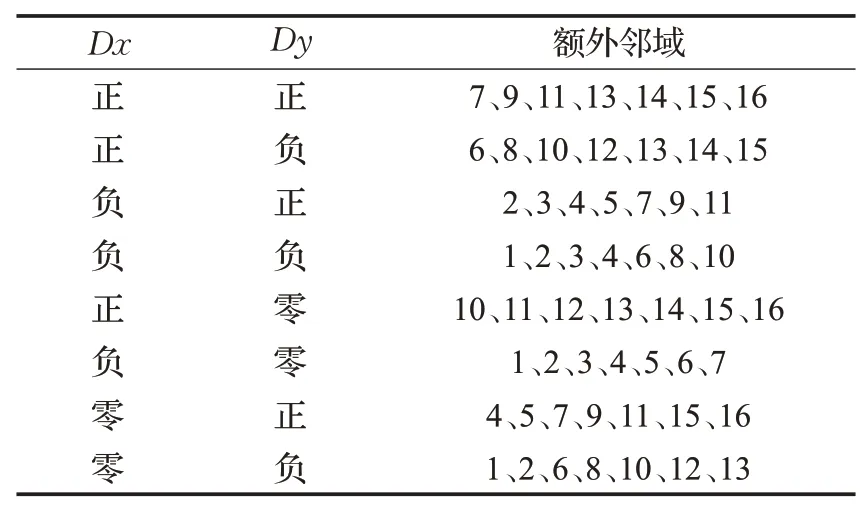
表1 引导向量对应搜索方向Table 1 Guide vectors and searching direction

由于额外邻域的数量影响算法的启发信息含量和计算量，算法的时间复杂度O(closesize×n)与邻域的数量n相关，其中closesize表示A*算法在完成搜索时对应的已搜索节点的数量。以图3所示的栅格地图为例，设定起点为地图左上角A点，目标点为地图右下角B点，栅格间一次横纵移动长度为10步，比较3邻域、5邻域、7邻域、9邻域、24邻域下的路径长度及搜索时间。

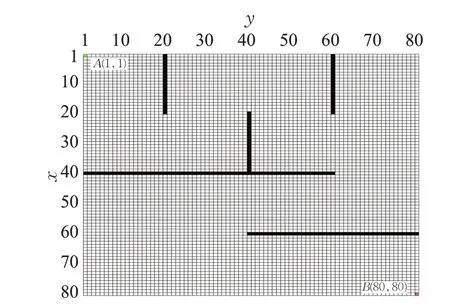
图3 邻域数量比较栅格地图Fig.3 Simulated map for number of neighborhood

如表2所示，3邻域和5邻域拓展由于自由度不够，导致路径长度最长，7邻域、9邻域、24邻域搜索获得路径最短，且7邻域的搜索时间最短，因此选定在引导向量方向上进行额外7邻域的搜索方式，提高搜索效率。

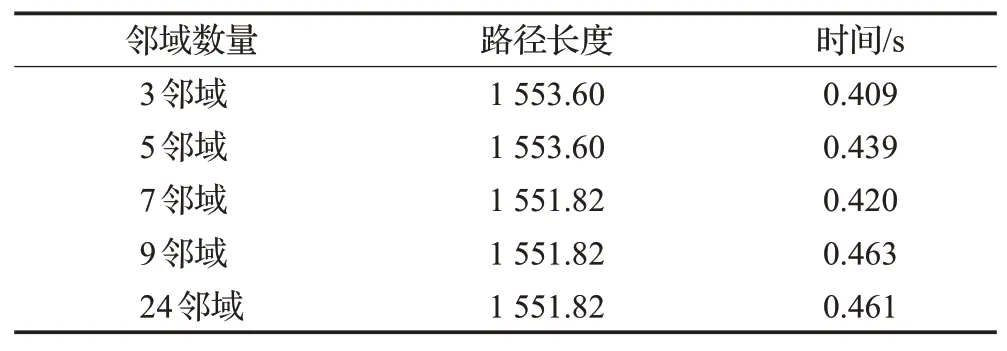
表2 邻域数量优化比较Table 2 Neighborhood number and performance items

1.3 路径平滑处理

为了优化路径，项目研究采用局部优化策略去除搜索冗余节点。如图4所示，图中黑色方块表示障碍物，白色方块表示自由通行区域，x1节点为起点，x6节点为目标点，从起点到目标点的黑色实线为初选路径，横纵移动一格的长度为10。

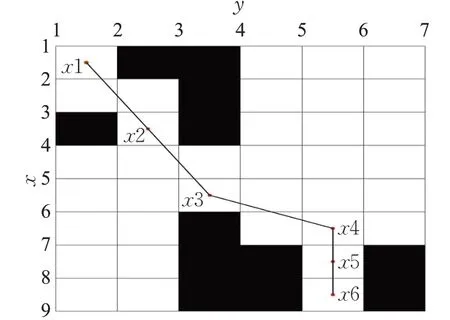
图4 初始路径示意图Fig.4 Original results of A*algorithm

依次遍历各节点，并判断其与其他节点形成路径为无碰撞相连，从而建立一个无向图网络。经过路径优化，剔除了x3与x4节点，最终获得图5所示{x1,x2,x5}路径。

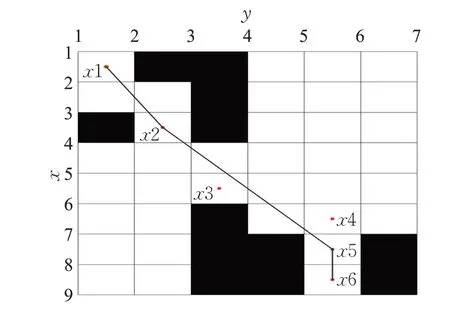
图5 优化路径示意图Fig.5 Path smoothing optimization results

具体平滑处理流程如图6所示：用集合S表示目前节点间最短路径；用集合Dn表示节点间非最短路径，n代表路径数。对集合S和集合D中的数据不断地迭代更新以便实现路径平滑处理。当集合S与集合D中的路径存在起止点一致的，即指对于当前节点，从起点开始有多种不同的方式可以到达。通过选择两个集合中起止点一致时路径长度的较小值，更新集合S中的节点数据，从而保证集合S中存储的是当前最短路径节点。当遍历完所有节点后，即获得各节点形成的可能路径方案，找到目前的最优路径。

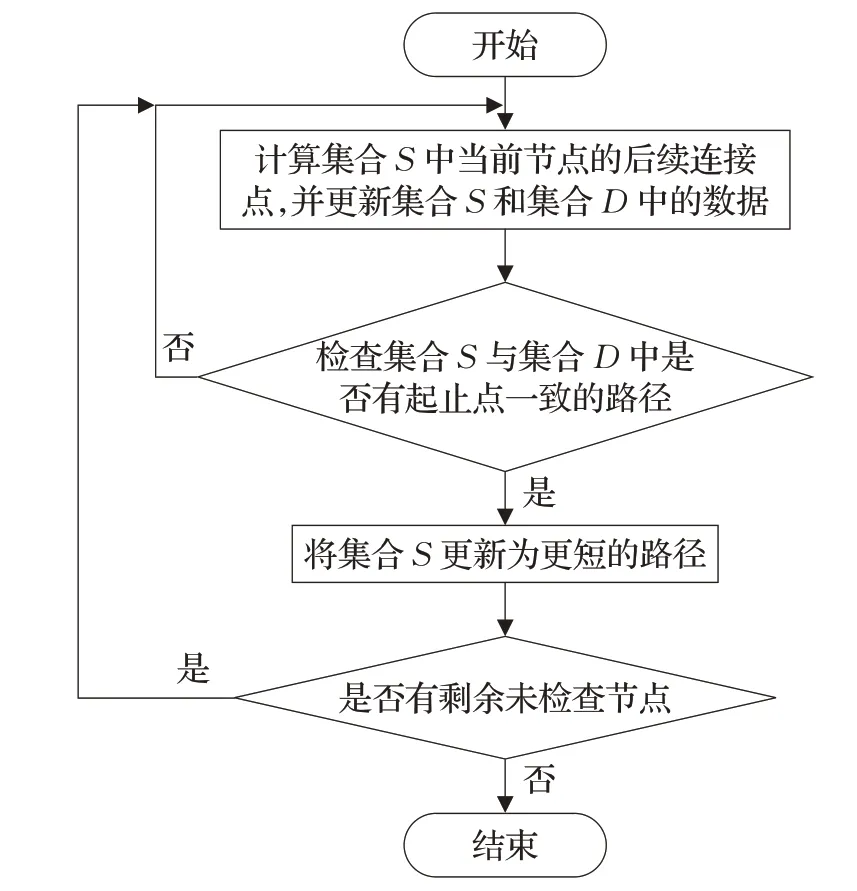
图6 平滑处理流程图Fig.6 Flow chart of path smoothing algorithm

因此，改进的A*算法实质是在传统8邻域A*算法的基础上，借助引导向量，优化搜索邻域，从而提高搜索效率；通过平滑处理步骤，剔除冗余的节点，进一步优化路径长度与平滑度。

2 仿真实验

2.1 随机栅格地图仿真

将改进后A*算法分别在不同地图、不同障碍率的条件下，进行仿真实验。选用地图大小分别为50×50、100×100、300×300的栅格环境来代表小地图、中等地图和大地图，障碍物的随机生成占比分别为10%、20%、30%、40%，模拟4类12种环境（见图7～图10）。在上述地图环境，选择中心A点为路径起点，右下角B点为终止点，定义栅格地图中一格横纵移动的长度为10，记录100次有效实验的路径长度和搜索花费时间。

图7 10%障碍占比三种地图Fig.7 Three categories of map under 10%obstacle scale

图8 20%障碍占比三种地图Fig.8 Three kinds of size of map under 20%obstacle scale

图10 40%障碍占比三种地图Fig.10 Three categories of map under 40%obstacle scale

如图11～图14所示，比较改进A*算法、24邻域A*算法、8邻域A*算法、24邻域的Dijkstra算法、RRT算法仿真实验效果。其中RRT算法采用了双向RRT算法，目标偏向概率为10%，搜索次数上限为30万次。

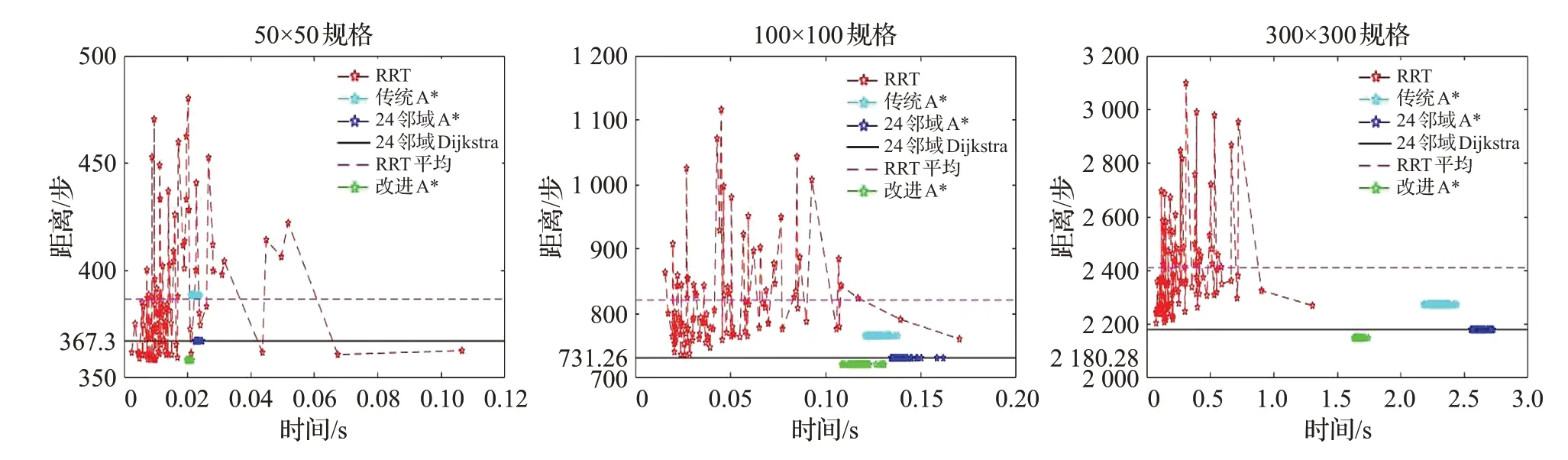
图11 不同地图10%障碍实验结果Fig.11 Results under 10%obstacle scale

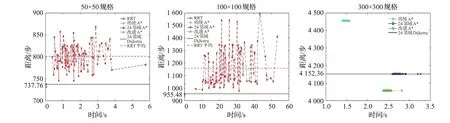
图14 不同地图40%障碍实验结果Fig.14 Results under 40%obstacle scale

可以看出：

图9 30%障碍占比三种地图Fig.9 Three categories of map under 30%obstacle scale

（1）改进的A*算法对比8邻域和24邻域的A*算法获得的路径更短，在每一类实验中均可以获得最短长度的路径。

（2）改进A*算法、8邻域A*算法、24邻域A*算法、Dijkstra算法每次搜索获得的路径长度固定，且A*类的算法搜索花费时间波动不大，说明这些算法性能较为稳定。

（3）在上述的12类环境下，RRT算法搜索花费时间以及获得的路径长度均有较大的波动，该算法性能不稳定。

路径优化目标包含两个方面，一是降低随机性影响，提升其路径查找的成功率，二是减少路径长度，提高路径搜索效率。因此，选择成功率(p)、100次平均路径长度(dˉ)、100次路径长度标准差(sˉ)、搜索最小花费时间(tmin)、搜索最大花费时间(tmax)等5个指标作为算法评价指标。为了验证实际地图下不同算法的性能，在300×300地图，不同障碍率下，计算各性能指标（见表3～表6）。

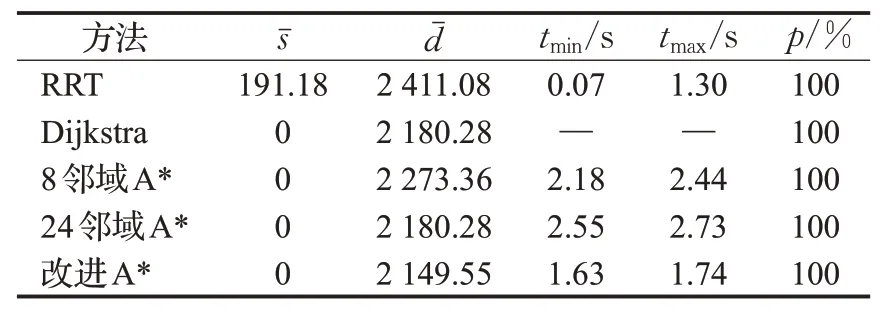
表3 300×300地图10%障碍物Table 3 10%obstacle scale in 300×300 map

表6 300×300地图40%障碍物Table 6 40%obstacle scale in 300×300 map

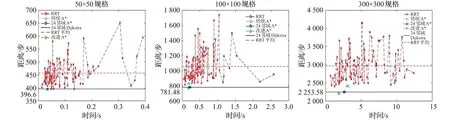
图12 不同地图20%障碍实验结果Fig.12 Results under 20%obstacle scale

图13 不同地图30%障碍实验结果Fig.13 Results under 30%obstacle scale

可以看出：

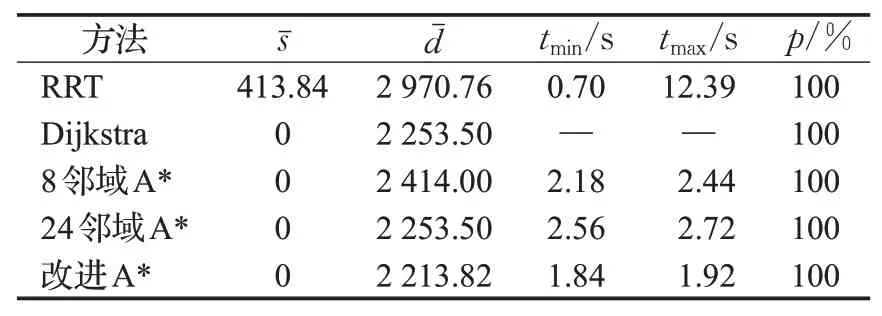
表4 300×300地图20%障碍物Table 4 20%obstacle scale in 300×300 map

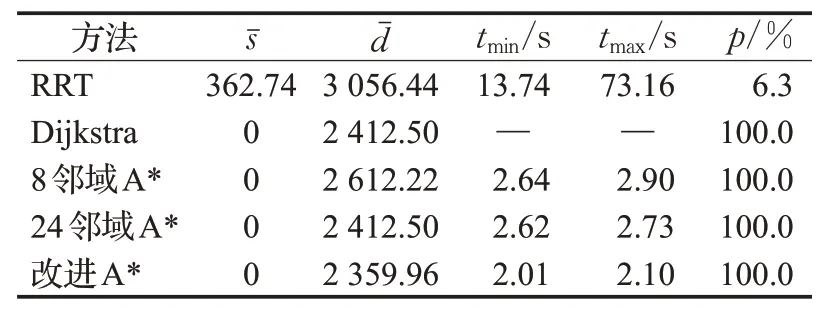
表5 300×300地图30%障碍物Table 5 30%obstacle scale in 300×300 map

（1）当障碍物占比较小，分别为10%和20%时，改进的A*算法（额外7邻域）具有100%的成功率，其每次均可求得最短长度的路径，因此路径长度标准差均为0，该算法在两种环境下对应的最大最小搜索时间差别不大，分别为0.11和0.08，说明该算法性能稳定。24邻域A*算法的最小搜索时间花费分别为2.55 s和2.56 s，与同条件下的8邻域搜索相比搜索时间更长。RRT算法的成功率可以保持在100%，其在两种情况下的路径长度标准差都是最大的，分别是191.18和413.84，说明随着地图障碍物占比的上升它表现得愈发不稳定，其最小搜索时间是最快的，但与最大搜索时间的差值较大，说明该算法性能不稳定。

（2）当障碍物占比为30%时。改进的A*算法有100%的成功率，且其每次均可求得最短长度的路径，其最小搜索时间是最快的。RRT算法的成功率急剧下降至6.3%，说明该算法不适用于此环境，其路径长度标准差依然最高，但是相比之前环境的结果下降至了362.74，原因是障碍物占比的提高对RRT算法的随机性起到了一定的限制作用，其算法的最小搜索时间是最慢的，与最大搜索时间的差值变大，说明该算法性能不稳定。

（3）当障碍物占比为40%时。改进的A*算法仍然可以保证100%的成功率，且求得的路径长度依然是最短的，其最小搜索时间略慢于8邻域A*算法。RRT算法在长时间的运行下仍不能获得至少一组解，因此不讨论其性能。

综上所述，在改变地图大小以及障碍物占比模拟出的12种环境下，改进的A*算法可以稳定地在各种环境下求出最短路径。在障碍物占比和地图大小增大后，RRT算法的性能均会受到影响，且障碍物占比的提升对它的影响更明显。Dijkstra算法也对应进行24邻域搜索。

2.2 实际地图仿真实验

模拟机场特种车辆的路径规划实验。将机场卫星地图进行栅格化处理，用于实际地图仿真实验。如图15所示，左上角A点为路径起点，右下角B点为目标点，获取20个有效实验结果（图16），其他实验条件与2.1节同。不同算法下指标量化计算见表7。

图15 实际地图栅格化Fig.15 Rasterization of real scene map

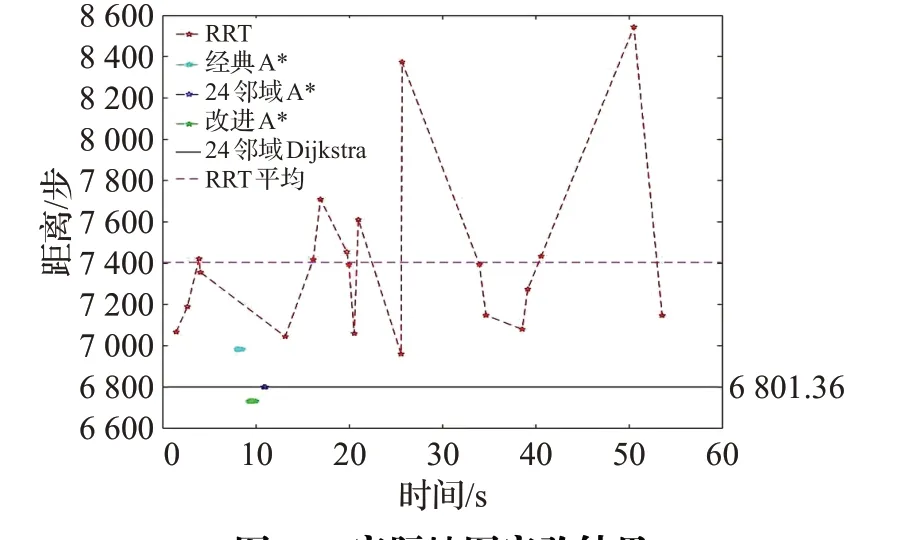
图16 实际地图实验结果Fig.16 Results in real scene map

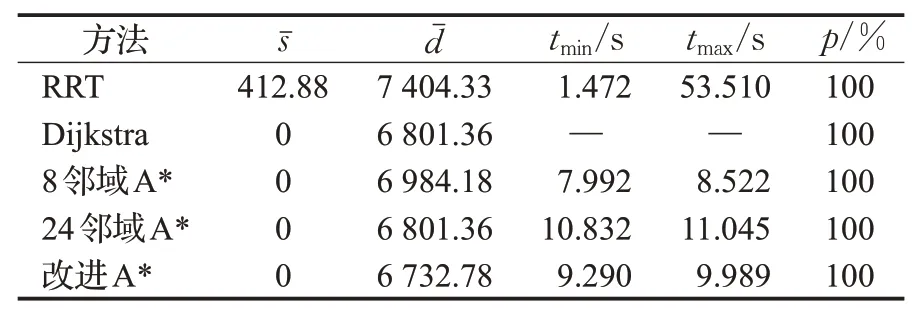
表7 实际地图仿真结果Table 7 Results in real scene map

可以看出RRT算法在该环境下搜索成功率为100%，它的路径长度标准差最大，为412.88，有最快的搜索速度，但是其搜索时间波动较大，为52.038 s，说明其性能不稳定；改进的A*算法可以稳定搜索出最短的路径，长度为6 732.78，且其时间花费波动较小，为0.699 s，搜索性能较为稳定。

实验结果表明在实际地图的仿真实验中，改进的A*算法依然能够稳定地求得最短的路径。

3 结论

改进A*算法是基于图搜索原理寻求路径最优的方法，该算法将传统A*算法的搜索邻域拓展至24邻域，提高算法搜索的自由度，引入引导向量，优化邻域数量减少无用探索，以便提高搜索效率，加入平滑处理步骤，减少冗余节点，进一步优化路径长度与平滑度。不同实验环境下，本文算法都可以稳定高效规划路径。