基于Voronoi图的方向区域查询方法

刘润涛，董庆宇，吴昊天

1.哈尔滨理工大学 信息与科学计算技术研究所，哈尔滨 150080

2.哈尔滨理工大学 理学院 数学系，哈尔滨 150080

方向区域查询是根据给定条件，在空间数据库中查找相应空间对象集的一种典型的空间查询类型，在地理信息系统（GIS）中具有重要的作用，其广泛应用在城市规划、交通以及物流管理等各个领域。方向区域查询的本质是根据所给定的方向及其他约束条件从数据集中找出方向区域内的所有空间对象。例如，若策划修建一条公路，则需要确定在预定方向以及一定宽度的区域内有哪些建筑物需要被拆除。方向区域查询因为其广泛的应用前景，成为重要的研究内容。

与其他空间查询方法一样，当面对庞大的数据量时，效率成为了人们关注的问题。为了提高方向区域查询的效率，学者们近年来提出了一些方法，其流程大致分为过滤和提纯2个步骤，在过滤过程中不需要查询区域的几何信息进行完整的计算而是需要高效的索引结构将有可能在查询区域内部的点加入候选集中，在该过程中可以舍去大量无关空间对象；对于提纯过程，在利用候选集的基础上进行严格的几何计算从而得到完全在查询区域内的正确结果集。由于提纯过程中涉及复杂的几何计算，故其通常比过滤步骤更加耗时。长时间以来，研究人员构造良好的索引结构使候选集减小或提出更有效的几何验证算法以降低提纯的计算成本。

近年来，较多方向区域查询方法被提出，其大多数是在R树[1]与其扩展的基础上进行的。这就使R树的缺点被引入。Papadias等人[2-3]提出使用R树结构检索方向关系，但研究的都是绝对方向上的查询（例如北、东）的索引机制和处理策略，为了实现绝对方向上的查询，其方法使用范围查询策略（RQS），但具有一定局限性。为了克服在R树索引上使用传统的范围查询策略处理基于对象的方向查询的局限性，Liu等人[4]提出基于开放形状的策略（OSS），该策略在遍历空间对象的过程中使用实际方向区域作为过滤器，从而尽早排除可能存在的错误结果。肖予钦等人[5]为了表示对象的MBR间的方向关系提出了一种四元组模型，同时利用上述模型和R树提出了一种针对方向关系查询的过滤方法，为了得到对象间的方向关系，根据MBR间方向关系的不同种类提出了相应的提炼方法，减少了计算消耗。张泽宝等人[6]在利用R树以及四元组模型方向关系的基础上提出了一种针对方向关系查询的精过滤方法，在传统的查询流程基础之上，加入了一个精过滤过程，减少了计算量。Liu等人[7]在已有方向查询算法的基础上，通过利用索引结构MB-tree，给出了针对方向查询策略的剪枝规则，使访问点的数量减少。Wei等人[8]利用包含空间对象内部和外部近似信息，提出了一种基于MRD-tree和开放形状模型的方向查询策略，该方法可以在过滤过程中排除大量无关对象。刘润涛等人[9]利用MBR在MB-tree中有序的特点，提出了一种针对被查询结点的MBR剪枝的规则，减少了I/O操作。王中辉等人[10-11]通过将方向以及空间距离关系相结合，提出了一种基于方向距离关系的方向空间查询方法，但由于查询模型的限制，查询结果可能在某些情况下出现一些偏差。

R树具有计算简便等优点，但R树在查询过程中存在大量中间结点重叠和覆盖的问题，即实际方向MBR区域远大于实际方向所覆盖的区域，从而使执行过程中访问了较多不必要的结点造成候选集包含大量的错误结果，使整体查询性能下降。为了提高方向区域查询效率可采用性能更佳的结构。本文针对这个问题，将Voronoi图结构引入方向区域查询。

Voronoi图[12-13]是计算几何领域中的一个重要内容，在空间查询等相关研究领域中得到了较多关注。此外，Voronoi图与Delaunay三角剖分[14]互为对偶图的关系已被广泛地应用。Voronoi图可以很好地表示空间数据的邻近关系，同时具有矢量以及连续平铺数据模型的基本特性，可以对空间数据进行很好的管理。鉴于Voronoi图具有的良好拓扑结构和几何性质，本文采用基于Voronoi图的方法进行方向区域查询。

为了获得完整的几何结构，本文利用Delaunay三角剖分形成Voronoi图。首先，为了形成初始Delaunay三角网，在对点集求凸壳后，将凸壳点集进行Delaunay三角剖分，然后采用逐点插入的方式对插入点所影响的局部区域进行修改更新，利用已形成的Delaunay三角网生成Voronoi图。对于给定的查询对象，利用首结点与查询对象连线形成的有向线段以及Voronoi图可以通过邻接生成点延展的特点确定查询点位置，同时以查询点位置为起点，利用Voronoi图结构进行延展，减少了数据的访问量，对于区域边界，利用空间对象与查询区域的关系分情况将相关点加入候选集中，减少对空间数据不必要的访问，从而提高查询性能。

1 基本定义及性质

定义1[15（]Voronoi图）给定一组生成点P={p1,p2,…,pn}⊂R2,其中2＜n＜∞,且当(i≠j)时，pi≠pj。其中，i,j∈In={1,2,…,n}。以下公式给出pi的Voronoi区域：

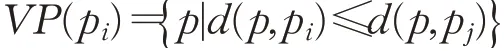
其中，j≠i,j∈In,d(p,pi)表示点p与点pi间的最小距离（欧几里德空间中点p和点pi间的直线距离）。其中点pi确定的Voronoi区域称为点pi的Voronoi多边形。

由V(P)={VP(p1),VP(p2),…,VP(pn)}构成的图形称为Voronoi图。点pi称为Voronoi生成点，共享相同的边的Voronoi多边形为邻接多边形，邻接多边形的生成点叫邻接生成点。

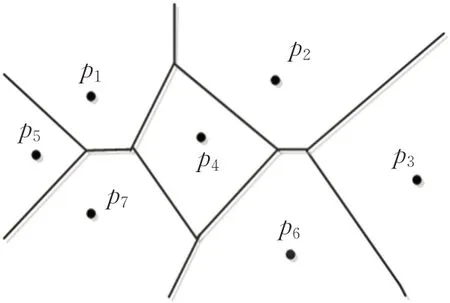
图1 Voronoi图Fig.1 Voronoi diagram

定义2[12]（Delaunay边）设三角网的边集为E,对于其中的一条边e,若存在一个圆经过e的两个端点，且圆内不含点集中的任何其他点，则称其为Delaunay边。

定义3[12]（Delaunay三角网）若点集的一个三角网中所有的边均为Delaunay边，则称该三角网为Delaunay三角网。

性质1[12]在点集S形成的Delaunay三角网中，每个Delaunay三角形的外接圆均不包含S中任意其他数据点；在点集S能够形成的所有三角网中，Delaunay三角网中的三角形的最小角度是最大的。

性质2[16]Voronoi图与Delaunay三角网对偶。

性质3[16]一个点集的Voronoi图是唯一的。

性质4[16]在Voronoi多边形中，每个Voronoi多边形平均有6条边，即每个生成点平均有6个邻接生成点。

2 Voronoi图存储结构

近年来，有关构建Voronoi图方法的研究很多，可以分为两大类。其中一类是直接生成，即不经过其余流程直接根据点集构造Voronoi图；另一类是间接生成，即利用性质1先对点集进行Delaunay三角剖分，然后构造Voronoi图。直接生成Voronoi图虽比间接生成Voronoi图的效率要高，但间接生成Voronoi图容易得到Voronoi多边形的结构便于研究和存储。本文将采用基于构建Delaunay三角网生成Voronoi图的方法。首先，在形成初始三角网的基础上，利用逐点插入法对点集中剩余点进行Delaunay三角剖分，形成点集的Delaunay三角网；其次，利用Delaunay三角网构造点集的Voronoi图，同时在生成过程中，对点、边等结构信息进行存储。

2.1 Voronoi图存储结构的构成

在Voronoi图存储结构中各类结点的结构为：

Vor结点：(pi,Vor-Pointslist,Vor-EdgesList,Vor-NeighborsList)

其中Vor结点中pi表示该点坐标；Vor-Pointslist表示Voronoi多边形顶点链表索引；Vor-EdgesList表示Voronoi边链表索引；Vor-NeighborsList表示该点的邻居链表索引；Vor-Point表示Voronoi顶点，其结点内p1表示该点坐标；PointArr表示共享该顶点的生成点；Vor-Edge表示Voronoi多边形的边，该结点内(pa,pb)表示该边两侧的生成点，(ph,pt)表示该边两端点；Vor-Neighbor表示邻接生成点（“邻居”），其中pi表示该点的索引。

2.2 Voronoi图存储结构的形成

在构建Delaunay三角网的过程中，首先生成点集的凸壳，并将凸壳进行Delaunay三角剖分生成初始三角网；将点集中其余点通过逐点插入的方法加入三角网中从而完成最终Delaunay三角网的构建。

对于凸壳的构建存在较多算法，考虑时间消耗等因素，本文采用Graham凸包求解算法。该方法首先对点集进行预处理，然后利用预处理后的点集，根据两点连线与第三点的方向关系判断是否存在于结果集中，最终生成凸壳点集。为了形成初始的三角网，主要思想为：对已形成的凸壳进行Delaunay三角剖分，利用生成的凸壳信息，每次找到一个由两条相邻凸壳边构成的三角形，同时确保没有凸壳上的其他点被包含在此三角形的外接圆内部，对相关信息进行更新并记录，依次执行，直至点集中最后剩下三个点，将各点相互连接形成三角形并记录，最终生成初始的Delaunay三角网。

在初始的Delaunay三角网基础上，采用逐点插入的方法形成点集的Delaunay三角网，如图2所示，该方法主要思想为：从初始三角网中找出包含新插入点的三角形；以包含该插入点的三角形为起点，利用存储的相关信息，找出外接圆包含新插入点的所有三角形，并形成三角形集，此三角形集的外边界即为该插入点的影响区域，删除三角形集中全部三角形，得到剖分空洞；将插入点与空洞中所有顶点依次进行连接，新产生的三角网满足性质1，即符合Delaunay三角剖分准则。

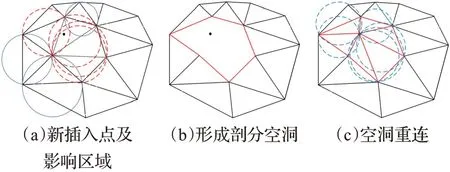
图2 插入点后Delaunay三角剖分Fig.2 Delaunay triangulation after insertion point

利用性质2，根据Delaunay三角网生成Voronoi图，如图3所示，其主要思想为：利用Delaunay三角网，对于凸壳上的边，从该边对应三角形外接圆圆心作指向该边外部且垂直于该边的射线；对于内部边，则只需连接该边两侧三角形外接圆圆心，依次处理Delaunay三角网中全部边，最终可得到Voronoi图。

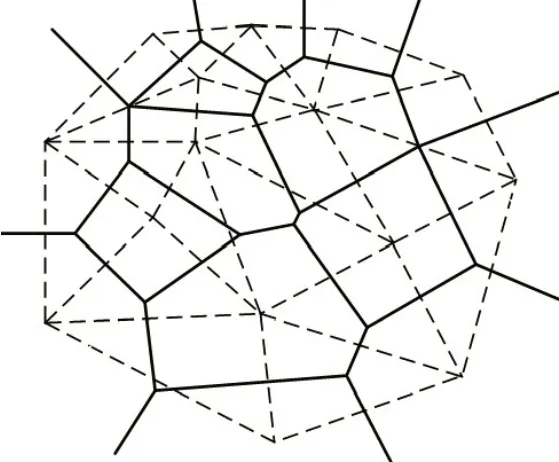
图3 利用Delaunay三角网生成Voronoi图Fig.3 Using Delaunay triangulation to generate Voronoi diagram

3 连续单方向开放区域及判定点与区域关系

3.1 连续单方向开放区域

开放区域是指部分边界被定义或边界超出所规定数据空间范围的几何区域。连续单方向区域指的是开放区域朝一个方向进行延伸。如图4（a）所示，给定查询目标q、宽度w以及角度θ，从点q两侧分别延伸w形成的p1和p2分别为连续单方向的两个起始点，n1和n2为分别以p1和p2为起始点的方向向量。如图4（b）和（c）所示θ∈[0,360]，且设定p1(x1,y1)和p2(x2,y2)两点满足x1＜x2或x1=x2,y1＞y2。

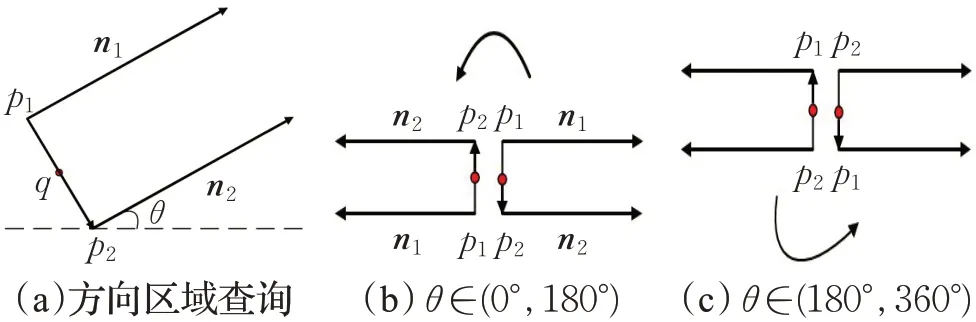
图4 方向区域查询模型Fig.4 Direction area query model

3.2 判断点与区域关系的条件

定理1已知一有向线段上的两点p(x p,yp),q(x q,yq),对于空间上任意一点s(x s,ys)，设：

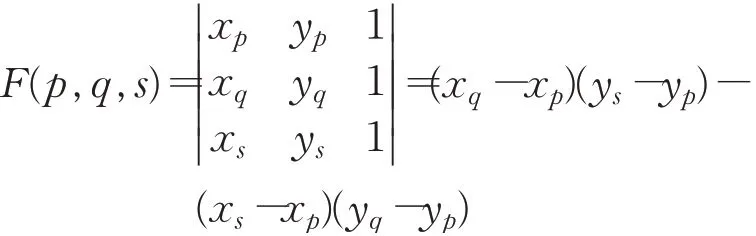
若F(p,q,s)＞0，则点s在该有向线段的左侧；

若F(p,q,s)＜0，则点s在该有向线段的右侧；

若F(p,q,s)=0，则点s在该有向线段上。

对于如图4（a）所示的方向区域查询模型，若空间中任意一点s(x s,ys)在查询区域内则应同时满足在p1p2的左侧，n1的右侧，n2的左侧。根据定理1基于如上讨论得到以下判定规则：

判定规则1对于空间中任意一点s(x s,ys)，设点q1为n1上除点p1外任意一点，点q2为n2上除点p2外任意一点。若有F(p1,p2,s)≥0,F(p1,q1,s)≤0,F(p2,q2,s)≥0成立，则点s位于查询区域内。

4 基于Voronoi图的方向区域查询

根据所给定的查询对象q以及所确定的查询区域，利用Voronoi图的拓扑结构与几何性质，进行基于Voronoi图的方向区域查询。首先根据Voronoi图结构找到查询对象所在位置，然后根据不同位置，按照规则将相应空间对象加入候选集，通过判断空间对象与查询区域的位置关系，根据规则加入候选集并判定是否为正确结果，从而得到查询结果集。

为了获得初始候选集，根据q所在位置分2种情况讨论：（1）查询对象位于生成点Voronoi多边形内；（2）查询对象位于Voronoi边上或位于Voronoi顶点上。为了使初始候选集中一定包含查询区域内部对象或与位于查询区域内部对象相关联的对象，给出以下判定规则。

判定规则2若对于任意pi∈S有q∈pi.VoronoiArea,则将pi.Vor-NeighborsList中对象加入候选集，其中S为数据点集。

判定规则3若对于任意pi∈S有q∈pi.Edge&q∉pi.Vor-Point，则将pi.Edge.(pa,pb)加入候选集；若q∈pi.Vor-Pointslist则将pi.Vor-Point.PointArr中对象加入候选集，其中S为数据点集。

根据点集中各点与方向查询区域的位置关系分2种情况讨论：

（1）该点位于方向查询区域内；（2）该点不在方向查询区域内，但该点的Voronoi顶点在方向查询区域内。

若假设pi∈QueryArea（查询区域），则存在(pk∈pi.Neighbors)∈QueryArea或(pk∈pi.Neighbors).Neighbors∈QueryArea；若pi∉QueryArea,但(pi.PointArr)∈QueryAre,则可能存在(pk∈pi.Neighbors)∈QueryArea。由于初始候选集中一定包含情况（1）或（2）的点，故只需考虑以上两种情况即可。基于以上讨论得出以下判定规则。

判定规则4对于一点pi∈S若pi∈QueryArea，则将点pi加入结果集的同时将pi.Vor-NeighborsList中所有点加入到候选集，其中S为数据点集。

判定规则5若pi∉QueryArea，但存在pi.Vor-Edge∩QueryAre，只将pi.Vor-NeighborsList中所有点加入到候选集。

定理2利用Voronoi图结构，从给定查询对象出发根据以上判定规则可以使查询区域中的点完全在候选集中，从而保证输出准确结果集。

证明在确定查询对象具体位置后，根据判定规则2和判定规则3可以确保使初始候选集中包含位于查询区域内的对象或尽管位于查询区域外但其Voronoi点在查询区域内的空间对象，之后根据判定规则4和判定规则5以及初始候选集中的点，利用Voronoi图结构进行扩展，使得查询区域内部对象以及与查询区域边界有关联的对象完全加入候选集。

根据以上判定规则以及定理2，本章提出基于Voronoi图的方向查询算法的主要思想为：首先判断查询点位置，该过程为将存储结构首结点与查询点连接生成向量，找到首结点与其邻接生成点连线中与向量夹角最小的为下一个点，从而替换首结点，依次执行，直至确定查询点位置；在确定位置后，根据规则1和规则2将相应点放入候选集中，之后从候选集中依次取出点，将区域内的点加入结果集中，根据规则3和规则4向候选集中加入新的点，直至输出完全结果集。在以上讨论的基础上，给出基于Voronoi图的方向查询算法，如算法1所示。

算法1Dir_Area_Query_Vor(Vor List,q,w,θ)

如图5所示，在基于Voronoi图的方向区域查询过程中，确定查询点具体位置后，建立区域模型，形成两个向量与一条线段所划定的查询区域，且标记√的Voronoi多边形为查询过程中被加入候选集中的点。

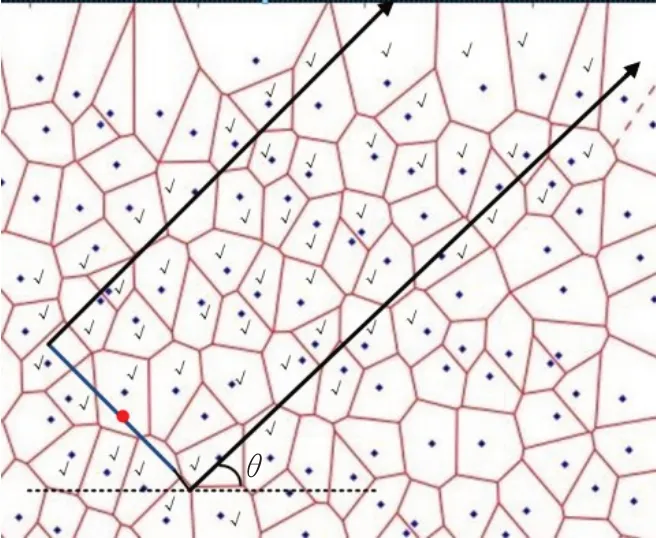
图5 查询过程模型Fig.5 Query process model

5 实验结果与分析

将本文给出的基于Voronoi图的方向区域查询算法与文献[7]中的基于MRD-树的方向区域查询算法进行比较。实验环境为：

（1）硬件环境：1.5 GHz CPU、4 GB内存、100 GB以上磁盘的个人计算机。

（2）软件环境：Windows 10 Professional操作系统，使用Visual Studio 2012编程实现。本文使用的数据集均为系统随机生成。

对于不同条件变量，本文进行以下测试项目：

（1）针对基于Voronoi图算法以及基于MRD-树算法在数据量不同情况下，对方向区域查询时所花费的时间以及I/O消耗进行比较。

（2）针对基于Voronoi图算法以及基于MRD-树算法在数据集密度不同情况下，对方向区域查询时所花费的时间以及候选集中非必要数据量进行比较。

图6、图7给出了数据集大小对于算法执行的影响，其中查询角度固定为30°，数据集大小为1×104～1×105，其中数据集中坐标值大小限制在0～1×105。由图6中可见，基于R-树的查询方法执行时间最长，其次为基于MRD-树的查询方法和基于Voronoi图的查询方法，且随着数据集逐渐变大时间消耗差距变大，这是因为基于Voronoi图的查询方法能够避开无效结点确定查询点位置，并且在查询过程中通过减少候选集中点的数量达到了减少大量几何计算的目的，从而加快了查询速度。图7给出了数据集大小对于I/O代价的影响，对于不同数据规模，基于Voronoi图的方向区域查询方法的代价低于其他两种方法。这是因为基于Voronoi图的查询方法在查询过程中能够减少更多非必要结点的访问使I/O代价降低。

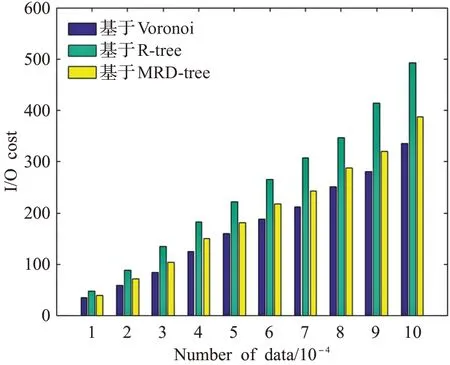
图7 数据量变化对I/O的影响Fig.7 Impact of data volume changes on I/O

表1给出了三种方法随着数据量变化各方法查询过程中候选集内数据量的对比，随着数据量不断增加，其他两种方法查询过程中候选集内数据量均大于基于Voronoi图方向区域查询方法，故该算法对于减少非必要数据点的访问效果较好且优于其余两种算法。

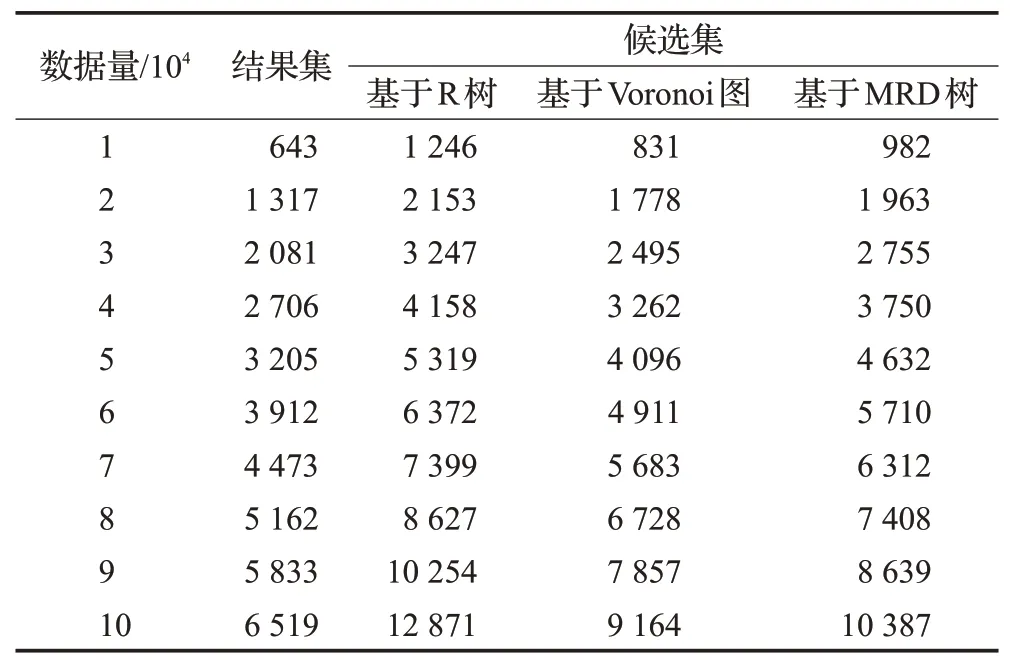
表1 三种算法的查询对比Table 1 Query comparison of three algorithms

图8、图9给出了方向区域查询中角度对于算法执行的影响，数据集大小为5×104，其中查询角度为0°～180°。由图8可见当查询角度不断变化时，基于R树的查询方法执行时间最长，其次为基于MRD树以及基于Voronoi图的查询方法，且该状态一直持续。由图9可见基于Voronoi图的查询方法的I/O消耗始终优于其他两种查询方法，且在0°～90°区间内基于Voronoi图查询方法与其他两种方法消耗差距最大，对应的角度为45°，在90°～180°区间内基于Voronoi图查询方法与其他两种方法消耗差距最大对应的角度为135°，这是因为基于R树以及MRD树的结构在查询过程中受到角度的影响造成查询过程中访问的MBR数量不同，且在45°和135°时访问MBR数量最多，从而导致I/O消耗增加，而基于Voronoi图的查询方法不受查询角度限制。

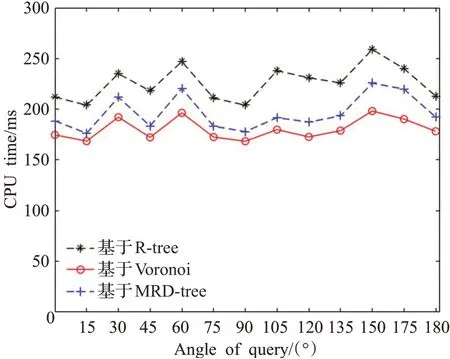
图8 查询角度变化对CPU消耗的影响Fig.8 Impact of query angle changes on CPU consumption

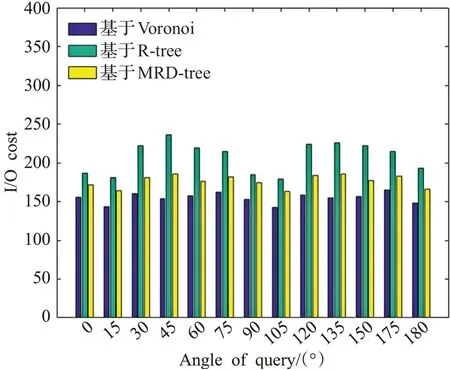
图9 查询角度变化对I/O消耗的影响Fig.9 Impact of query angle changes on I/O consumption

6 结束语

本文基于对空间数据方向区域查询的研究，提出了一种基于Voronoi图的方向区域查询方法，该方法利用Voronoi图的存储结构，根据Voronoi图几何结构以及可以通过邻接生成点延展的特性，大幅度减少了在确定查询对象位置以及查询过程中非必要结点的访问，从而达到了提高方向区域查询效率的目的且得到了准确的查询结果。理论分析和实验结果表明，该算法能够准确获得查询结果并具有较好的查询性能。未来将对基于Voronoi图的其他种类查询进行研究。