基于深度学习的矩阵分解推荐模型

纪佳琪，蔡永华+，郭景峰

(1.河北民族师范学院 数学与计算机科学学院，河北 承德 067000；2.燕山大学 信息科学与工程学院，河北 秦皇岛 066000)

0 引 言

在海量数据中获取有价值信息是大数据时代面临的一大问题，虽然搜索引擎能够根据关键词快速地检索到有用信息，但是这种检索是同一的且不是个性化的。推荐系统可以很好地解决个性化推荐问题，它根据用户的历史行为数据为用户匹配自身需求。在早期的推荐模型中，使用的训练数据大多是用户对物品评分的显式数据[1]，由于不同用户对同一物品的评分存在差异较大，一种带有偏置项的矩阵分解技术解决了这个问题[2]。为了解决显式数据稀疏性的问题，引入了额外数据到矩阵分解模型，如基于社交关系的矩阵分解模型[3]、使用物品内容和评论的基于主题的矩阵分解模型[4]等。然而，仅仅使用显式数据的推荐模型并不能产生较好的推荐结果，为此一些研究使用收藏、购买等隐式数据对推荐结果有了一定的提高[5,6]。近些年深度学习[8-10]理论也成功地应用到了推荐系统，如使用显式数据基于受限玻尔兹曼机的推荐模型[10]、基于自编码器和降噪自动编码机的推荐模型[11]等。这些研究成果的核心思想是使用显式数据通过学习他们间的深度隐结构来完成推荐。也有一些研究使用隐式数据基于深度学习的推荐模型，如协同降噪自动编码器[12]使用隐式数据构建用户偏好，神经协同过滤[13]使用多层感知神经网络对用户和物品的交互进行建模。上述研究只使用显式数据或隐式数据通过深度学习进行建模，本文将同时使用显式数据和隐式数据，提出了一种基于深度神经网络的矩阵分解模型用于解决推荐问题。

1 相关工作

使用U表示用户，U={u1,u2,…,uM}，共M个用户。使用I表示物品，I={i1,i2,…,iN}，共N个物品。R∈M×N表示用户评分矩阵，其中每一项Rij表示用户i对物品j的评分，该评分可以是显式的，也可以是隐式的。显式评分是用户根据自己的喜好程度给予物品的评价分，如在购物完成后给予1颗星表示1分，给予2颗星表示2分以此类推，一般情况下评分值可取1至5的整数，分值越高表示用户对该物品喜好程度越大。隐式评分是指用户的收藏、购买等行为折合成的评分，一般用1和0表示，如有上述行为用1表示，没有上述行为用0表示。

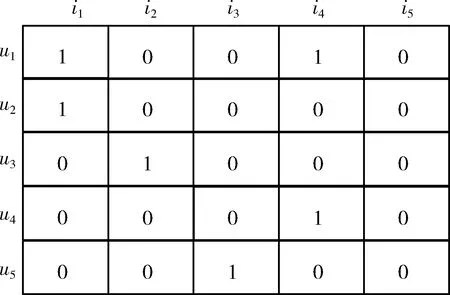
图1 用户评分矩阵

因需要同时考虑显式数据和隐式数据，因此不能像图1那样简单处理。由于评分矩阵中应既包括显式数据也应包括隐式数据，因此用户i对物品j的显式评分用原始值表示(一般情况下为1至5的数值)，用户i对物品j的隐式反馈用1表示，未知项用0表示，如图2所示。本文认为R矩阵中的数值表示了用户对物品的喜好程度，数值越高表示喜好程度越大。

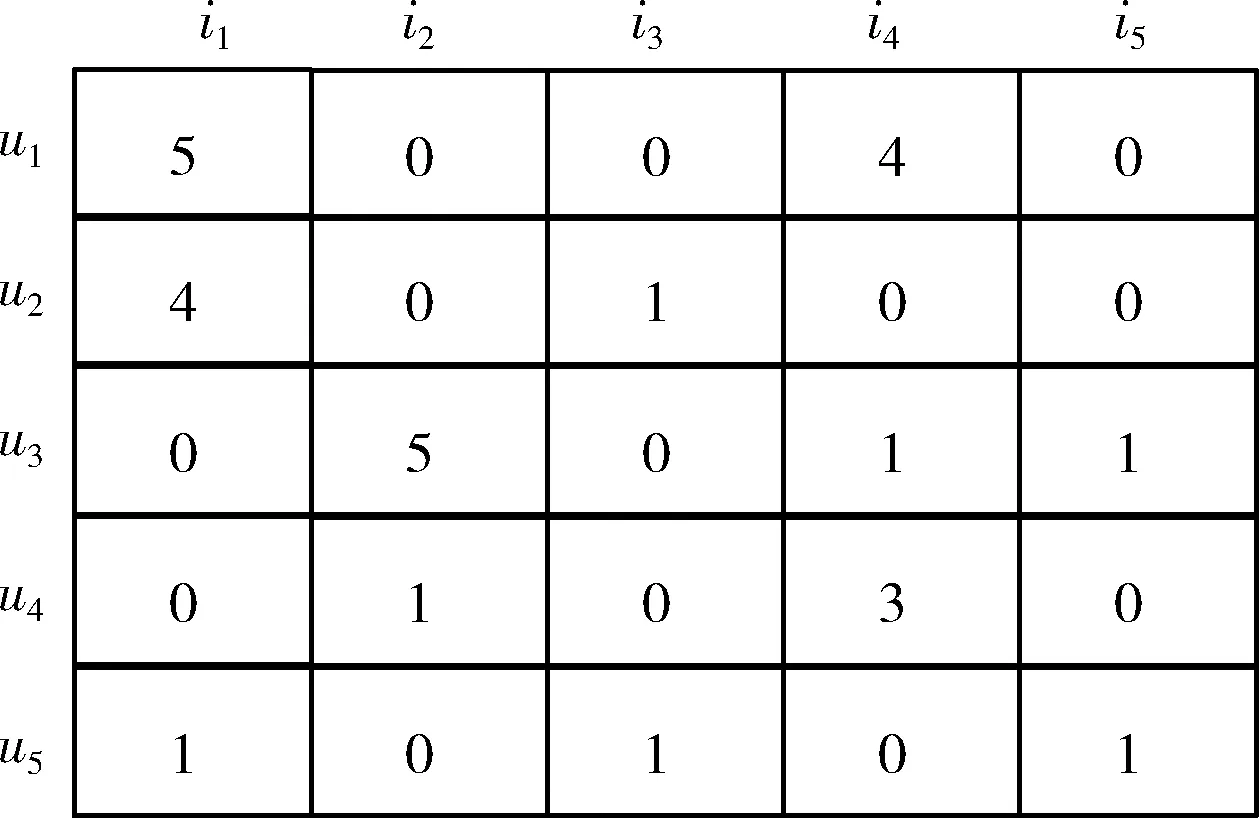
图2 改进的用户评分矩阵

(1)

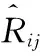
(2)

式(2)中，pi和qj分别表示用户隐向量和物品隐向量。在神经协同过滤[13]模型中，使用多层感知机来学习f，此时的f是非线性的，能够表达用户和物品间深度复杂的交互关系。

本文，我们综合运用了上述两种思想，首先把矩阵分解技术和深度神经网络结合起来，通过一个深层次的网络架构学习用户隐向量和物品隐向量，然后通过用户和物品隐向量的内积得到预测评分，从而完成推荐任务。

2 模型设计

本节首先给出本文设计的深度神经网络架构，通过这个架构能够把用户和物品用低维隐向量表示，然后定义我们重新设计的损失函数和优化方法，最后进行模型的训练。

2.1 深度神经网络架构

本文使用两个分别含有多个隐藏层的全连接深度神经网络，与一般深度神经网络不同的是本文的深度神经网络输出层并不是一个概率值，而是特征向量。然后对这两个特征向量再做点积运算得出评分预测值。

图3描述了本文提出的深度神经网络架构。输入层使用的输入数据是第1节图2描述的评分矩阵R，其中Ri*表示矩阵R的第i行，即第i个用户对所有物品的评分。R*j表示矩阵R的第j列，即所有用户对物品j的评分。由于R∈M×N，显然Ri*∈N，R*j∈M。

图3 深度神经网络架构

(3)

ReLU(x)=max(0,x)

(4)

同理，图3深度神经网络架构中右侧是用来生成物品隐向量qj部分。与左侧部分相似，可以形式化的用式(5)表示。其中上标q用来表示图3深度神经网络架构中右侧用来生成物品隐向量qj部分，其余符号含义与式(3)中符号含义相同

(5)

提取到用户特征隐向量pi和物品特征隐向量qj后，可以通过计算这两个隐向量的内积得到用户i对物品j的评分预测值，具体计算方法如式(2)所示。

在上述所提的架构中pi和qj不再由传统的矩阵分解方法生成，pi和qj是深度神经网络对Ri*和R*j相关运算后提取生成，而提取方法充分地利用了深度神经网络强大的特征自动抽取能力，因此pi和qj能够更好的抽象表示用户隐向量和物品隐向量。

2.2 损失函数

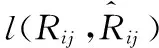
(6)

为了使2.1节提出的深度网络架构得到较好的训练，上述传统的损失函数并不能满足要求，需要从新设计待优化的损失函数，本文把损失函数的一般形式表示为式(7)。其中R+表示观测到的数据，即显式数据和隐式数据，称为正例；R-表示未观测到的数据，即R矩阵中我们设为0的数据项，称为负例。在实际训练中，由于数据量过大(共M*N条数据)，因此并不会使用所有负例参与训练，而是抽取一定的比例的负例参与训练，具体抽取比例的大小将会在后面小节的实验中给出。为了公式符号的简洁，本文仍使用R-代表抽样过的负例数据

(7)

待优化目标中损失函数的定义尤为重要，假设只使用显示数据，可以把评分预测转换为回归问题，此时可以使用平方差损失函数，其定义如式(8)所示

(8)

其中，θij是待优化参数表示当前训练数据Rij的权重。然而该损失函数无法对隐式数据和抽样的负例数据进行训练，因为这两类数据的值只为1或0，此时可以把评分预测转换为二分类问题，为此可以使用二分类交叉熵损失函数对这两类数据进行训练如式(9)所示

(9)

由于本文同时使用了显式数据和隐式数据，因此在综合考虑了式(8)和式(9)的特点后设计了一个全新的损失函数如式(10)所示，该损失函数能够对显示数据和隐式数据同时进行优化。该损失函数主要是在训练时对训练数据进行归一化，即所有训练数据都除以R矩阵中的最大值(max(R))。经过这样的处理，训练数据的范围会限定在0和1之间，因此可以使用类似交叉熵损失的损失函数

(10)

2.3 模型训练

结合2.1节提出的深度神经网络架构和2.2节提出的损失函数，得到了最终待优化的目标函数，本节给出模型优化过程的详细算法，详见算法1。

算法1：深度神经网络推荐模型优化算法

Input:R,neg_ratio,iter_num

初始化:

(2)设置R+为R中不为0的项

(3)设置R-为R中所有为0的项

(4)对R-进行随机采样，其采样个数满足|R-|=neg_ratio*|R+|

(5)设置训练集T=R+∪R-

(6)设置M=R中行数，N=R中列数

(7)fortfrom 0 toiter_num:

(8)forifrom 0 toM:

(9)forjfrom 0 toN:

(10) 使用式(3)计算pi

(11) 使用式(5)计算qj

(13) 使用式(10)计算损失函数

3 实 验

本节将展开一系列实验验证本文提出模型的有效性，同时根据实验结果确定不同超参数的设置，如网络层数、每层的神经元数、负例采样率(neg_ratio)等。

3.1 数据集

本文实验中使用的数据集为MovieLens 1M和MovieTweetings 10k，其详情见表1。

表1 数据集详情

MovieLens 1M(https://movielens.org/)：数据集的提供者已对该数据集进行过清洗，保证了每个用户至少有20条评分信息，每个物品至少有5条评分信息，评分值从1-5。该数据集包含了6040名用户对3706首歌曲的1 000 209条评分信息。

MovieTweetings 10k(http://research.yahoo.com/Academic_Relations)：来自于Twitter的电影分级数据集，评分值从1-10。该数据集包含了3794名用户对3096部电影的10 000条评分。

3.2 评价指标

本文使用5折交叉验证得出最终的实验结果，使用命中率(hit rate，HR)和归一化折损累积增益(normalized discounted cumulative gain，NDCG)作为评价指标。HR@n表示在推荐的n个物品中，能够命中至少一个的比例，该值越高越好。NDCG@n表示在推荐的n个物品中，不仅命中，而且排序尽量正确，同样该值越高越好。

3.3 超参数选择

3.3.1 负例采样率

在算法1中，需要从数据集的负例中采样一定比例的负例作为最终训练数据，我们通过这个不同的采样率值(neg_ratio，neg_ratio@1表示采样率设置为1)，观察各评价指标的变化。从表2中看出随着采样负例采样比例的提高，HR和NDCG的值程上升趋势但该趋势逐渐缓慢，随着采样比例的进一步提高，HR和NDCG还有下降趋势。考虑到采样越多的负例，其训练时间越长，并且无限增加负例数并不能无限提升系统性能，权衡之后本文取neg_ratio的值为5。

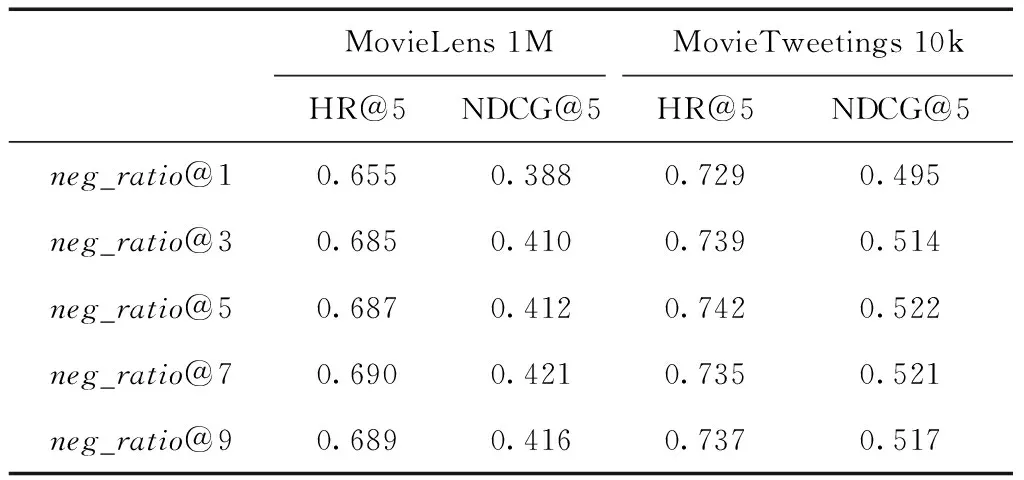
表2 不同负例采样率对评价结果的影响

3.3.2 深度神经网络层数及每层的神经元数

本文提出的模型中，是通过一个深度神经网络把用户和物品映射到一个隐向量空间中。由于网络层数及每层的神经元数的组合有无穷多种，因此不可能穷举所有情况进行实验。结合其它研究神经网络学者的一些指导意见，即隐藏层数过多和神经元数过多不一定对性能有极大的提升，反而可能还会产生梯度消失或梯度爆炸问题造成性能的急剧下降。因此，我们首先尝试了隐藏层数从1-5增长，每层神经元个数相同，负例采样率设为1。由于篇幅原因，只列举了在两个数据集上HR的实验结果如图4所示。由于当隐藏层数为4和5时HR值迅速下降，失去了比较意义，因此未在图中画出，这也说明无限增加隐藏层数并不能带来性能的持续提升。

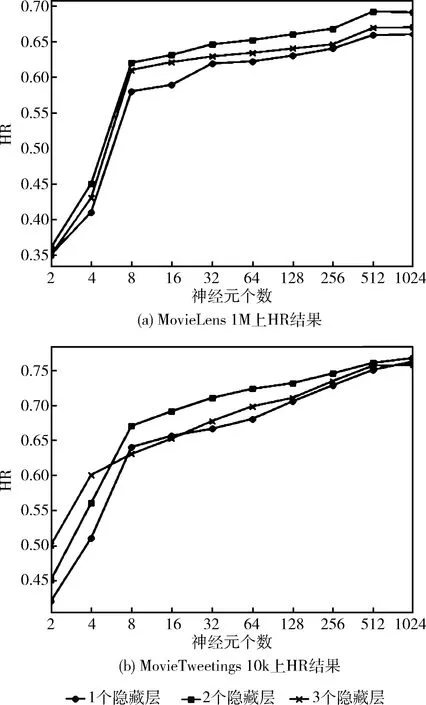
图4 神经网络层数及神经元个数对结果的影响

从图4中我们还可以看出，无论在哪个数据集上，当隐藏层个数为2的时候性能最好。当我们变化隐藏层神经元个数时，可以看到性能整体成上升趋势，其中当神经元个数从2增长到8时，上升趋势很明显，说明过少神经元不能够很好地进行特征表征，当神经元个数从8增长到1024时，上升趋势开始变得平缓，说明持续增加神经元并不能无限提高系统性能。当神经元从512增长到1024时，系统性能还有下降趋势。根据以上分析，我们把神经元个数设定为512。

3.3.3 隐向量长度选择

使用深度神经网络的目的是把用户和物品转化为用户隐向量和物品隐向量，而隐向量的长度会对最终推荐结果产生影响，因此我们分别设置这个隐向量的长度从32到256得出的实验结果见表3。从表3中可以看出，当隐向量的长度为128时，推荐结果最好。

表3 隐向量长度对推荐结果的影响

通过上述3部分实验，得出模型最佳超参数。即神经网络中的隐藏层数为2，每个隐藏层都包含512个神经元，输出的隐向量长度为128(即向量pi和qj的长度)，负例采样率为5。再接下来的对比实验中，默认都使用上述超参数。

3.4 与基线模型比较

为验证本文提出模型的有效性，选取了ItemKNN(item-based collaborative filtering)[15,16]，eALS(element-wise alternating least squares)[17]作为比较模型。

ItemKNN：基于物品的协同过滤算法，是推荐系统中较早的算法，目前已广泛用于工业界。

eALS：该算法使用隐式数据，通过对缺失数据赋予不同权重，使用矩阵分解方法，取得了良好的推荐效果。是目前基于矩阵分解方法取得较好推荐结果的算法之一。

图5显示了本文提出的模型和其它模型在两个数据集上HR@5和NDCG@5的比较结果。从结果中可以看出无论HR@5指标还是NDCG@5指标，本文的模型都由远优于其它两个模型(如：本文模型在MovieLens 1M数据集上HR@5指标比ItemKNN和eALS分别提升14.9%和3.1%)，说明本文提出的深度神经网络架构能够很好捕获物品和用户之间的隐关系，提取到了比较合理的用户隐向量和物品隐向量，结合显式数据和隐式数据并经过合理设计的损失函数后，本文模型取得了良好的效果。

图5 与其它模型比较结果

4 结束语

本文提出了一个基于深度学习的矩阵分解推荐模型，通过精心设计的深度神经网络架构，把用户和物品映射成低维空间的用户隐向量和物品隐向量，然后通过这两个隐向量的内积得到用户对物品的评分预测。模型中的训练数据包含了显式数据和隐式数据，为此设计了一个损失函数能够同时计算这两类数据的损失。通过与其它模型的比较，从实验结果可以看到本文所提出的模型在推荐性能上有较大提升。

在接下来的工作中的，我们将继续调整深度神经网络结构，以需求更好的特征提取。同时考虑使用卷积神经网络或循环神经网络对一些富信息进行提取，然后融合到推荐算法中以获得更好的推荐效果。