基于卷积LSTM模型的航空器轨迹预测

刘龙庚，翟俐民，韩云祥+

(1.中国软件评测中心，北京 100089；2.四川大学 视觉合成图形图像技术国防重点学科实验室，四川 成都 610041)

0 引 言

随着计算机技术不断发展，各行业的信息量急剧增长，一般将规模巨大且无法通过常规软件工具在合理时间内管理和处理的信息称为大数据，目前业界普遍认为大数据的特征可以归纳为4个“V“-Volume(大量)、Velocity(高速)、Variety(多样)、Value(价值低)[1]。传感器数据是大数据的主要来源之一，对传感器网络的大数据分析和应用，是信息技术的发展趋势和重点研究方向[2]，Liu L等深入研究了大数据环境下传感器网络基础技术[3-5]。空中交通管理过程中需要不断收集航空器相关传感器数据，天然具有大数据的特点，除了传统的大数据特征之外，还具有以下特点[6]：①体量巨大，空管一年产生的数据在PB级别以上；②种类繁多，在空管过程中涉及到多种数据，包含静态数据、动态数据、结构化数据、非结构化数据；③来源真实，空管数据直接采集自空管一线，来源真实可靠。

在空管大数据开发方面，美国处于领先地位[7]。国内在空管大数据开发方面也做出了一些探索。空管大数据可实现空管运行过程智能化精细化，空管大数据可用于空管流程优化和空管风险管理与评估，空管大数据可直接用于空管仿真模型的构建，并据此实现航空器运行过程预测，准确、可靠的空中交通轨迹预测模型(TBO)可以有效提高空中交通运行效率并进一步保障运行安全。

目前关于航迹预测的方法主要有基于航空器性能参数、运动学模型的传统方法以及基于数据挖掘和混合机器学习的研究方法。石庆研等[8]提出了一种在线更新LSTM网络的短期航迹预测算法；李旭娟等[9]提出了一种自动生成的条件变分自动编码器，以编码-解码的形式直接对未来一段时间的航迹进行预测；Xu等[10]提出了一种新的Social-LSTM模型，为空域内的每个航空器建立LSTM网络，并通过一个池化层整合关联航空器的状态，从而编码了航空器之间的相互作用；马兰等[11]基于ADS-B数据挖掘和统计分析，并使用CURE聚类分析；Shi等[12]提出了一种基于LSTM的轨迹预测模型，该模型解决长期依赖问题，避免了相邻序列状态的动态依赖性，有助于提高精度；Gallego等[13]针对目前的航迹预测方法缺少对于空中交通中不确定因素的理解，提出了融入航空器周围交通状况的航迹预测方法；Liu等[14]提出了一种基于树的高效匹配算法从气象数据中构建特征图，并构建了一个端到端的卷积神经网络，该网络包含一个LSTM编码网络和混合密度的LSTM解码网络，进一步从历史飞行轨迹中学习时空相关性；Shi等[15]提出了一种4D航迹预测模型，该模型长短期记忆网络结合滑动窗口来维持长期特征并预测轨迹，并将环境信息作为输入特征；Zeng等[16]针对目前的空域状态轨迹方法在终端区这样复杂的空域中效果不好的问题，提出了一种seq2seq的深度长短期记忆网络预测模型，可以有效地捕获长期和短期的时间依赖；Giuliari等[17]将自然语言处理领域的热门模型Transformer应用在轨迹预测中，并分别实现了原始的Transformer网络和BERT，实验结果表明Transformer在数据存在缺失的情况下表现更好；本文基于空管大数据分析挖掘，利用聚类算法萃取航迹数据，并构建LSTM网络航空器轨迹，使用航迹信息进行仿真验证，实现对航空器轨迹的准确预测。

1 数据处理

根据数据的来源的组织形式，可将空管大数据初步划分为静态数据、动态数据、结构化数据、非结构化数据[6]，其中静态数据是在一定时间段内保持稳定的数据，动态数据与静态数据相反，主要包含了航空器运行时数据。本文采集了动态的航空器轨迹数据、机场天气数据和静态的进场标准仪表进港程序用于构建航空器轨迹预测模型。通过一定渠道获取双流国际机场2019年6月至2020年12月每天进离岗航班相关数据[18]，包含解析标准ADS-B航迹数据以及二次雷达数据，编写爬虫收集双流机场对应日期的METAR天气数据报。对于从多种渠道获取的原始航迹数据及气象数据不能直接作为训练数据集，需经过以下处理流程：数据清洗、多源数据融合、离散特征编码、模型数据集构建。数据清洗是剔除航迹点缺失过多的航迹。多源数据融合是指将来自不同数据源的轨迹数据及气象数据进行整合，使得航迹数据特征更加丰富。数据编码是指将特征中离散数据通过特征规则化，使其满足神经网络模型输入格式，让机器读懂该特征的含义。数据预处理过程如图1所示。

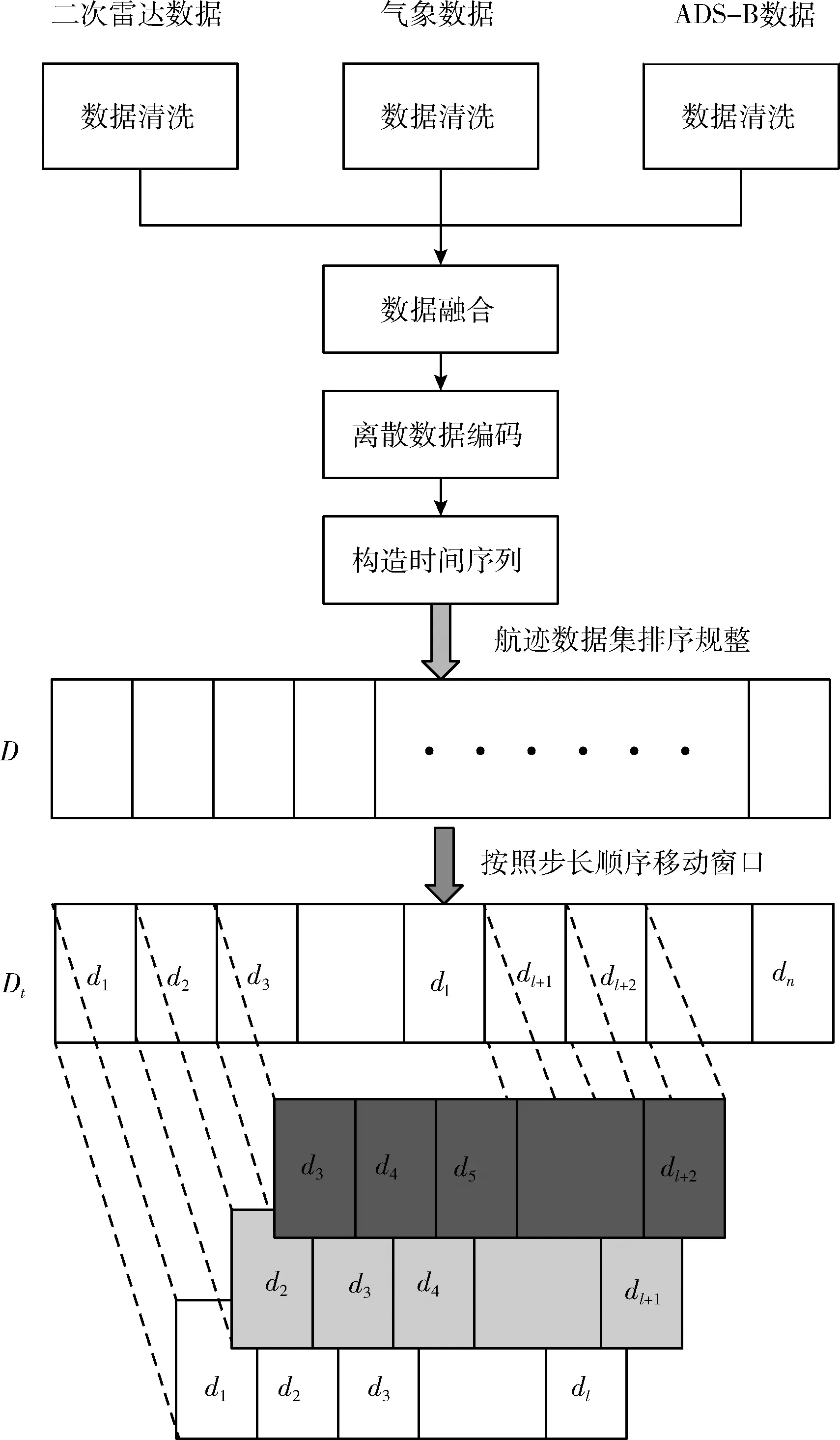
图1 数据预处理过程[19]

ADS-B以及二次雷达中的坐标数据为经纬度，为减少后续计算量，将航迹中的经纬度(B,L)通过墨卡托投影，转换为以双流国际机场为坐标原点的坐标系(X,Y)。坐标系转换关系如式(1)～式(3)所示

(1)

Y=K×(L-L0)

(2)

(3)

其中，标准纬度B0，标准经度L0，e为第一偏心率，e′为第二偏心率，a为长半轴长，b为短半轴长。使用一定对应规则将采集的ADS-B航迹数据、二次雷达数据、机场METAR数据进行融合，作为完整的训练集。ADS-B航迹数据与二次雷达数据通过飞行日期date和航空器呼号ID匹配，在确定为同一航班之后，使用时间戳插值的方法构造数据集，对于过程中差异较大的数据使用均值操作，如式(4)所示

(4)

上式中，(xradar,yradar)为航迹点p(i,j)记录的二次雷达位置坐标，(xabs-b,yabs-b)为航迹点p(i,j)记录的ADS-B坐标，(xi,j,yi,j)为融合后的航迹坐标。最后为了消除不同特征之间量纲不同导致模型训练困难的问题，使用归一化和标准化对数值型特征进行处理，方法如式(5)～式(6)所示

(5)

(6)

其中，X为特征数据集，x为原始特征数据，x′为归一化后的特征数据，max(X)、min(X)分别为该特征中的最大特征值与最小特征值，μ(X)、σ(X)分别为该特征中的期望与方差。

2 航迹聚类

作为一种无监督的机器学习方法，聚类在诸多领域应用广泛。聚类将具有类似特征的对象使用划分标准分为不同类别，目前常用的划分标准有欧式距离、马氏距离、曼哈顿距离等。在航迹聚类中，需要将类似的飞行轨迹划分为同一类，从最初选定的航迹簇开始，通过距离度量选定相近的航迹簇，不断合并航迹簇后重新计算航迹簇间距离，最终获得聚类结果。在计算的过程中，需要使用航迹间距离衡量航迹相似性，以判断是否将航迹簇合并。由于设备误差等现实原因，每条航迹长度通常不等，故无法使用常规的距离度量算法。动态时间规整(dynamic time warping，DTW)通过计算航迹点之间的最短距离，能够计算出航迹间的距离。针对两条航迹，其计算过程是将其航迹点分别作为行列，排列为一个二维表，并使用DTW公式计算航迹点间距离，从二维表的左上角到右下角寻找一条距离最短的路径，将这条路径上的距离和作为两条航迹间的相似度量。将训练样本中的所有航迹，两两计算航迹间的相似性，得到一个二维航迹矩阵，其大小为航迹数量，对于航迹集合T，通过DTW算法计算得到的航迹距离矩阵如式(7)所示

(7)

其中，d(Tj,TJ)为第j条航迹与第J条航迹之间的相似度。在计算距离矩阵时，使用快速DTW，其使用约束搜索空间的策略，可以降低时间复杂度，加速计算过程。

使用航迹聚类，将航迹分类并在此基础上建立不同预测模型，可以有效提高轨迹预测的精度。本文构建基于快速动态时间规整距离度量的并行剪枝层次聚类算法。在计算航迹相似度中，使用DTW算法；使用批次运算更新距离矩阵；及时剪枝远离聚类中心的离群航迹。具体流程：①计算航迹距离矩阵。对于训练集中的所有航迹，数量为nt，计算两两之间的相似度，得到nt×nt的距离矩阵，相似度计算使用DTW算法；②计算航迹簇之间的相似度；③遍历相似性矩阵中的航迹，获取其中距离最近的航迹，形成航迹簇对；④计算航迹簇对之间的簇间距离，比较与设定的簇间距离，小于预设则剔除，大于预设则为一个类别并重新计算所有航迹簇的距离矩阵，进行下一步迭代。使用预先设定的航迹数目阈值来判定航迹簇是否为离群航迹簇，当其中航迹数量大于阈值时，当前航迹簇成为一个航迹类别，否则该航迹簇为离群航迹簇，将被剔除。上诉过程为一次聚类算法的迭代过程，重新计算航迹簇的距离矩阵进入下一轮迭代。计算过程前需要设定两个关键参数，分别是离群航迹距离和离群航迹数目。

3 模型构建

航迹序列是一种时间序列，目前常用LSTM处理时间序列问题，相对于RNN而言，LSTM解决了其存在的长期依赖问题，能够学习长期依赖关系。LSTM的网络单元中每个重复模块由3个门组成，分别是遗忘门、输入门和输出门，每个门可以选择性地决定前一层的信息以什么样的方式传递给当前层，LSTM网络单元结构如图2所示。

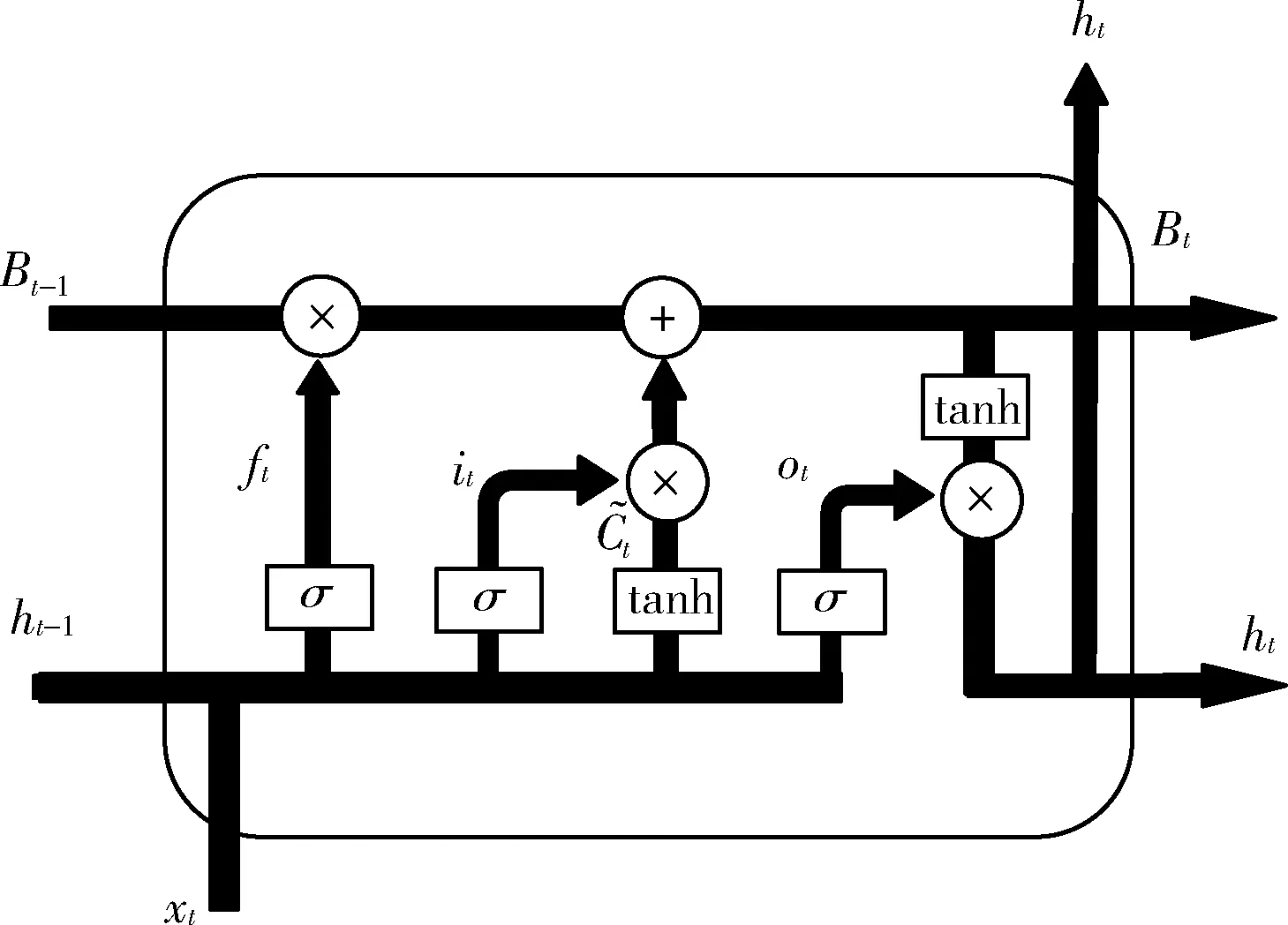
图2 LSTM网络单元结构

其中，σ和tanh分别是sigmoid激活函数和tanh激活函数，xt为t时刻的输入，ht为t时刻的状态，it为t时刻输入门输出，ft为t时刻的遗忘门输出，ot为t时刻输出门输出，结合图2，对于上述定义如式

ft=sigmoid(αf·[ht-1,xt]+βf)

(8)

it=sigmoid(αi·[ht-1,xt]+βi)

(9)

ot=sigmoid(αo·[ht-1,xt]+βo)

(10)

(11)

(12)

ht=ot*tanh(Bt)

(13)

图3 基于StackedLSTM航迹预测模型架构

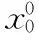
根据不同数据类型，LSTM具有多种变体，ConvLSTM是其中的一种，与原始LSTM的区别在于其使用卷积计算来代替权值计算，使用卷积提取多维数据中隐含的关联信息，在LSTM单元的遗忘门、输入门和输出门之前都添加一次卷积操作，这样做的目的是通过卷积在多维数据中提取特征，使其更加适合空间序列。ConvLSTM网络单元结构如图4所示。

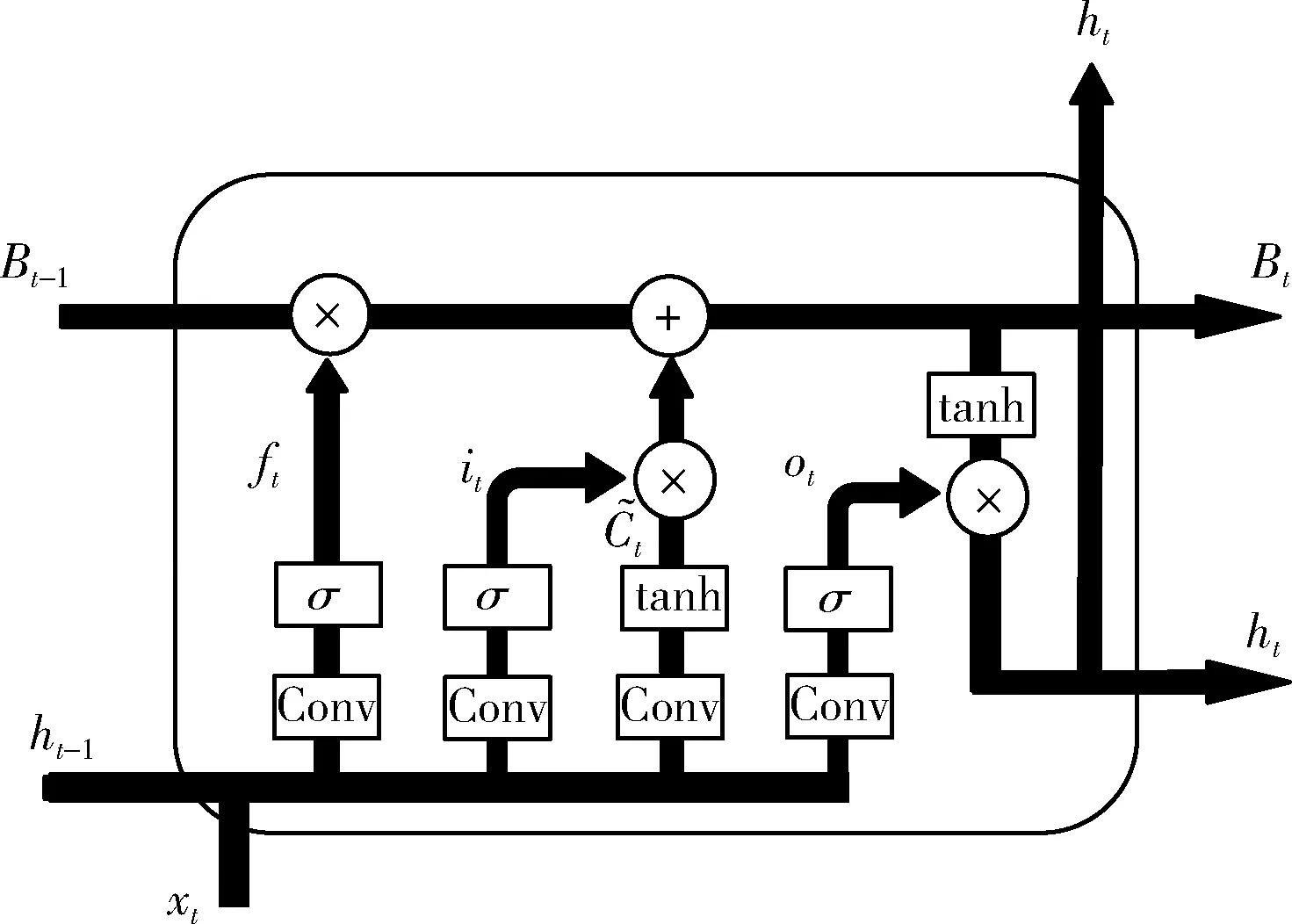
图4 ConvLSTM网络单元结构

相应的，网络单元中的每个门对应的计算公式也发生了变化，ConvLSTM的单元计算公式如下所示

ft=σ(Wxf*Xt+Whf*Ht-1+Wcf⊙Ct-1+bf)

(14)

it=σ(Wxi*Xt+Whi*Ht-1+Wci⊙Ct-1+bi)

(15)

Bt=ft⊙Bt-1+it⊙tanh(Wxc*Xt+Whc*Ht-1+bc)

(16)

ot=σ(Wx0*Xt+Wh0*Ht-1+WC0⊙Ct+bo)

(17)

Ht=ot⊙tanh(Bt)

(18)

式中：σ为Sigmoid激活函数；W为权重值；X为输入数据；H为输出数据；B为状态信息；b为偏差量；tanh为tanh激活函数。

ConvLSTM最早被应用于降雨问题预测，用于处理时空序列预测问题，后来也被应用在时间序列问题中。针对4D航迹预测问题，本文基于ConvLSTM单元构建了航迹预测模型，与Stack LSTM预测模型相比，ConvLSTM虽然包含了相同数量的隐藏层，但是将原始的LSTM单元替换成了包含CNN卷积操作的ConvLSTM单元；在模型输入层中，输入的数据为三维张量而不是一维数据；与原始的LSTM模型中大小为s的时间窗口序列对应，ConvLSTM模型的输入数据被划分为3个子序列；在模型的最后，仍然通过全连接层输出模型的最终结果。基于ConvLSTM航迹预测模型构架如图5所示。

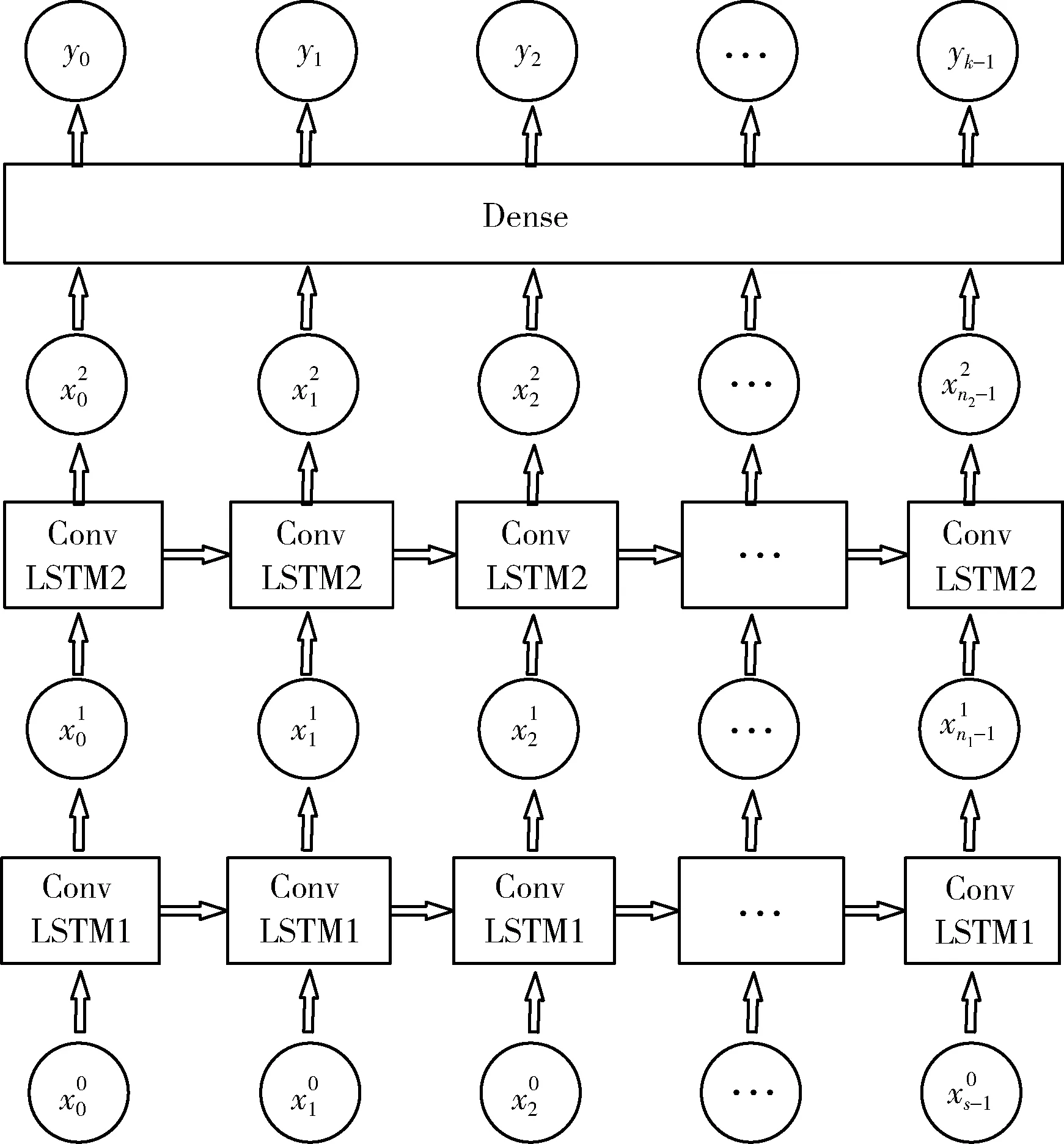
图5 基于ConvLSTM航迹预测模型架构

4 实验及结果分析

将获取的原始雷达报文数据解析，并通过数据分析等方法剔除不合理数据后得到航迹数据集。再对航迹进行航迹聚类，将数据集转换为聚类后数据。最后使用归一化和标准化将数据转换为标准模型输入。使用航迹中的三维位置坐标进行轨迹聚类，将航迹数据中不同航路的航迹分类。使用墨卡托投影将原始航迹中的经纬度坐标转换为以机场坐标为中心的二维平面坐标值以便后续计算，并对数据进行归一化处理以避免特征间量纲不同带来的影响。最终获得维度为9405*3的数据集。对于样本集中机型和分类结果是非数值类型，对其使用One-Hot编码。训练样本的特征包含时间戳、飞行器三维坐标、航向、速度、垂直速度、机型和聚类结果。训练时使用滑动窗口移动数据，将初始滑动窗口大小设置为9，即将航迹中前9个航迹点作为训练样本，模型输出下一个航迹点后窗口向后滑动，不断输出航迹点直到输出最后一个航迹点。使用水平误差、垂直误差和时间误差评估模型，水平误差为预测航迹点C和真实航迹点T在二维平面下的欧式距离，垂直误差是垂直方向上航空器的实际飞行高度和预测高度之前的距离差，时间误差是指两条航迹中对应航迹点的时间差值，计算公式如下所示

(19)

evert=|hT-hC|

(20)

etime=|tT-tC|

(21)

其中，水平误差以海里为单位(nm)，垂直误差以英尺为单位(ft)。使用平均绝对误差(mean absolute error，MAE)和均方根误差(root mean squared error，RMSE)衡量预测航迹和实际航迹之间的误差大小，其计算公式如式(22)～式(23)所示

(22)

(23)

其中，Pi为第i个航迹点某个特征的预测值，Ri为第i个航迹点某个特征实际值。使用双流机场航班进港航迹作为测试数据集，分析了DTW、快速DTW(FastDTW)、传统层次聚类(HC)，以及加入剪枝的改进层次聚类(IHC)在不同航迹点数下的实验结果，在时间开销上进行评价，结果见表1，聚类结果可视图如图6、图7所示。

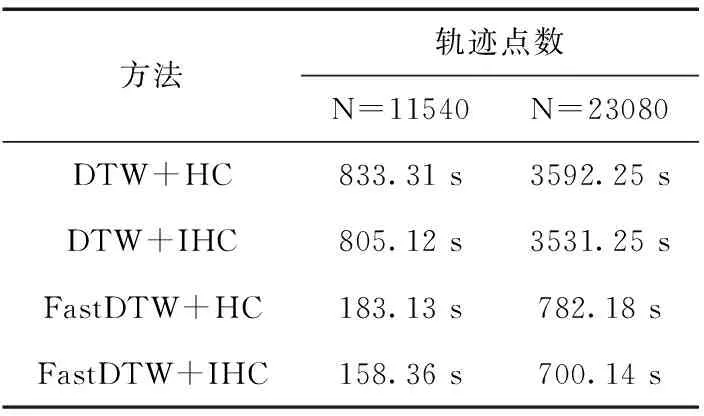
表1 聚类算法时间对比

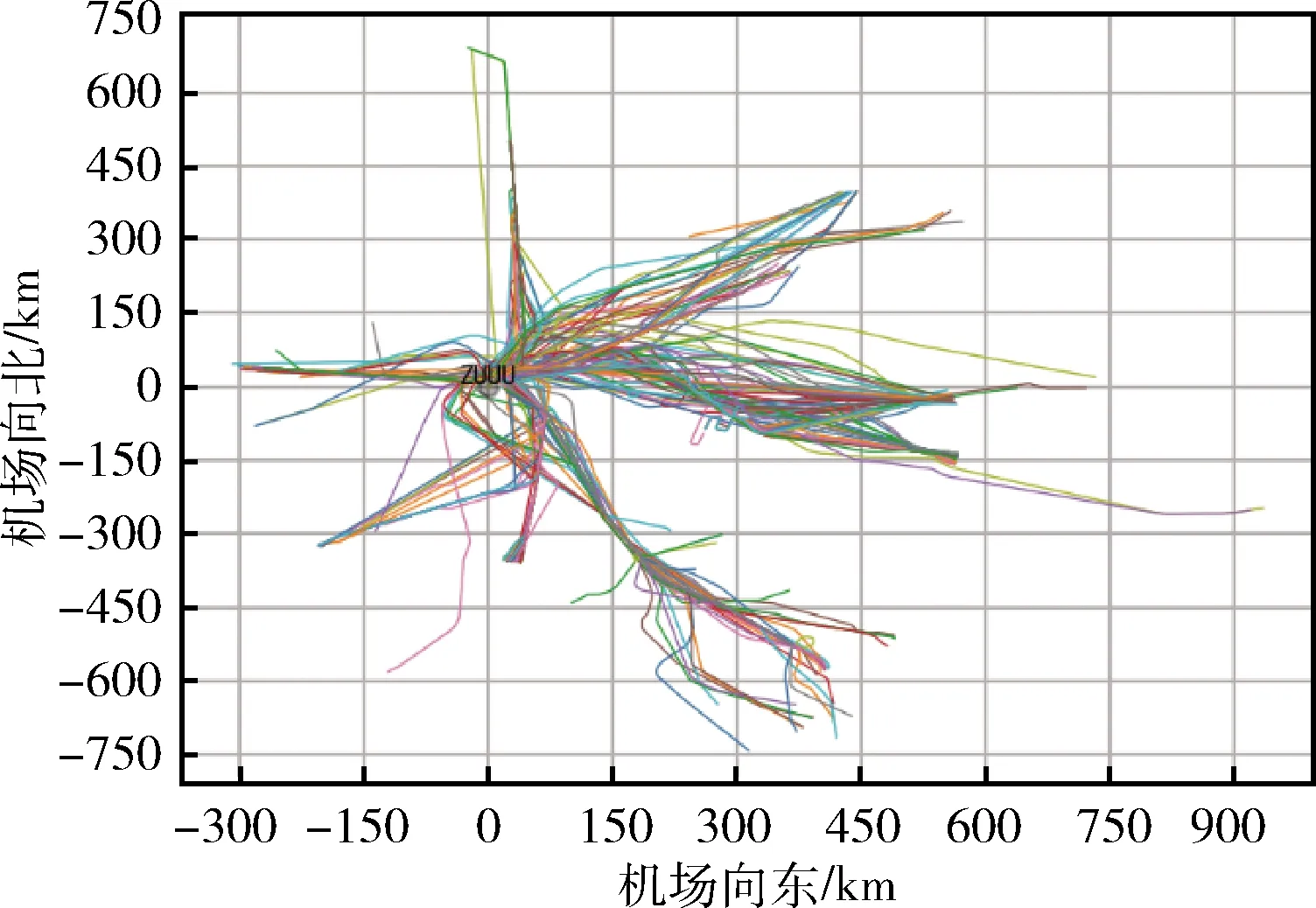
图6 原始航迹二维平面

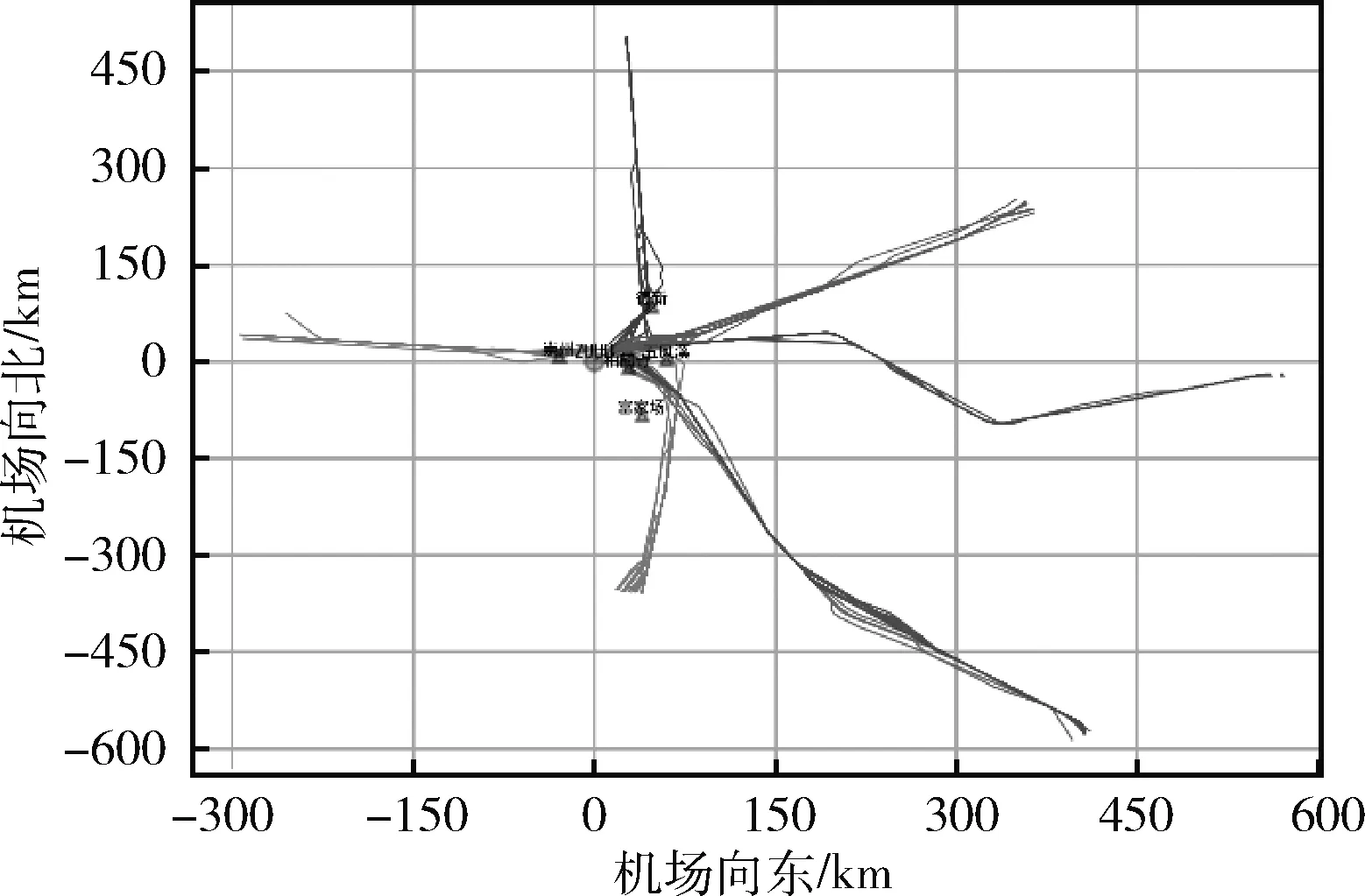
图7 聚类后二维平面

通过实际结果可知，该聚类方法将原始航迹分为6类，可以有效分离数据，将各类数据分别作为测试样本对航迹预测模型进行对比实验。在基于LSTM的预测模型中，包含两层LSTM隐藏层，单元个数均为300，为防止模型过拟合，在LSTM隐藏层后使用比例大小为0.2的Dropout，滑动窗口大小设置为9。基于ConvLSTM的预测模型中，将滑动窗口大小拆分为3、1、3，在输入层之后，包含两个ConvLSTM的隐藏层，每一层设置卷积核大小为(1，3)，通道数个数为256。随机选取60条航迹作为测试集，数据集剩余部分作为训练集。以测试集中一条航迹为例，预测模型的评价指标计算过程如下：①通过模型不断迭代计算预测点，获得一条预测航迹；②通过航迹点之间最短欧式距离的方式匹配样本标签航迹中的航迹点，计算预测点与实际点之间的各项误差值；③得到单条航迹的各项误差后，使用MAE和RMSE计算所有测试集误差。实验结果见表2。

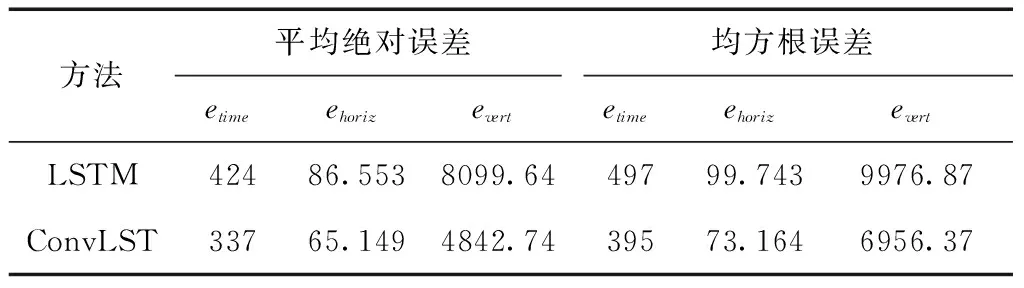
表2 误差分析对比

可以看出ConvLSTM预测模型的各项误差值均低于LSTM模型，其中，时间误差减少了87 s，垂直误差减少了21.404，水平误差减少了3256.9，由此看出ConvLSTM模型预测效果更佳。

5 结束语

本文从空管大数据出发，使用数据挖掘聚类算法构建数据集，在聚类算法中使用DTW算法和剪枝加速聚类，实验结果显示聚类时间开销从3592.25 s下降到700.14 s，构建LSTM预测模型和ConvLSTM预测模型，通过计算模型的MAE和RMSE，结果显示ConvLSTM预测模型的各项误差值均低于LSTM模型，时间误差减少了87 s，垂直误差减少了21.404，水平误差减少了3256.9。本文借助数据挖掘和神经网络等技术对4D航迹预测开展了研究工作，但仍然存在较多有待改进的不足之处，其主要包含：①目前数据源较为单一，随着民航大数据技术不断发展，可以从不同设备中获取航迹数据以供后续研究，后续工作可以获取多源航迹，利用大数据技术对数据进行融合，提供更加完备的数据集；②在预测中仅考虑历史航迹，并未将气象因素和空域态势融入模型，下一步可以将空域气象和空域态势输入模型，提高预测模型的鲁棒性和精确性。