基于W距离自编码器半监督生成模型

王江晴，何开杰，孙 翀，帖 军，尹 帆

(1.中南民族大学 计算机科学学院，湖北 武汉 430074；2.中南民族大学 湖北省制造企业智能管理工程技术研究中心，湖北 武汉 430074)

0 引 言

传统的监督学习通常需要大量的标签样本对模型进行训练，以便获得较好的质量，同时，由于维度灾难的原因，在处理高纬数据(如视频、语音和图像分类等)时，训练高质量的模型所需要的标签样本数量进一步呈现指数暴涨趋势[1]。

随着大数据时代的数据需求日益增长，海量的标签样本需求成为传统监督学习发展的阻碍之一，传统监督学习已无法满足人们的需求。半监督学习由于在标签样本数量很少的情况下，通过在模型训练中引入无标签样本来避免传统监督学习在训练样本不足(学习不充分)时出现性能(或模型)退化的问题，有着广泛应用。

近年来，半监督学习的研究工作主要集中在分类问题[2]。半监督深度分类模型主要目的是鼓励分类器将学得的条件分布逼近原数据的总体分布，当前半监督深度学习算法并没有充分考虑样本中无标签数据所包含的信息，半监督分类器并没有学习到真实的原数据的总体分布。针对该问题，本文根据迁移学习中的领域自适应(domain adaption)，将半监督学习中有标签数据集看成源域，全体数据集看成目标域，采用基于Wasserstein距离的Wasserstein自编码器(wasserstein autoencoder，WAE)生成模型与半监督学习相结合的方式，使得源域上训练的数据可以迁移到目标域中。本文从边际分布出发，使得优化目标既考虑有标签样本和无标签样本特征空间的边际分布和总体数据的边际分布相似，也考虑有标签样本的分布和总体的全概率分布相似，同时采用新的距离度量对模型拟合分布与真实数据分布之间的距离进行度量，从而学习到更加复杂的高维分布，将样本中无标签数据纳入分类器所学分布当中，学习到原数据的总体分布，最终使半监督深度分类算法可以学到原数据的总体分布。

1 相关工作

半监督深度学习算法训练模型的方式之一是采用生成模型。生成模型诸如生成对抗网络(GAN)[3]和变分自编码器(VAE)[4]通过对数据分布进行建模来捕捉样本之间的相似性，生成与原数据近似的拟合数据，半监督器学习模型期望通过生成模型学习到原数据的总体分布。

Semeniuta等[5]采用条件VAE建立鲁棒的结构化预测算法，在输入中加入噪声。M.Ehsan等[6]提出用于半监督学习的半监督变分自编码器，用Infinite Mixture模型处理半监督数据，采用带有不同混合系数的VAE的混合，让样本可以自动学习模型数量，但效果并不理想。Maaløe等[7]提出ADGM模型，引入辅助变量，建立更具有表现力的分布，提高预测性能，但也使得模型参数计算量过大。Cai等[8]提出MSVAE模型，该模型的双层解码器一定程度上克服了生成样本不够清晰的缺点，生成的样本尽管有所改进，但仍然较为模糊。采用KL散度和JS散度的生成模型均会产生样本模糊的问题，当高维空间中的两个分布之间距离没有重叠，KL散度和JS散度便会失去意义，无法度量分布间的距离。

Odena等[9]提出ACGAN，将标签信息和噪音一起输入到生成器中，使得ACGAN适合处理半监督数据。然而当前GAN模型大都难以训练并且会出现模式崩溃情况[10]。针对上述问题，Salimans等[11]提出采用经验技术来稳定GAN模型的训练，Arjovsky等[12]提出WGAN模型，采用Wasserstein距离替代KL散度和JS散度，改变了生成器和判别器的目标函数，并对判别器施加Lipschitz约束以限制判别器的梯度，基本消除了简单数据集上的模式崩溃问题，其中Wasserstein距离又称为推土机距离，当高维空间中两个分布没有重叠时，Wasserstein距离仍能够准确反映两者之间的距离。Tolstikhin[13]认为WGAN中的方法只适用于其本身，并改进Wasserstein距离与VAE生成模型相结合，使其可以应用于任何损失函数中，同时提出WAE模型。

WAE的做法使得模型对样本数据分布支撑集的拓扑限制更少，从而能学到更加复杂的数据分布[14]，但WAE作为无监督生成模型，只考虑到了无标签的信息，无法直接应用于半监督学习中，同时，现有的半监督与VAE结合过程中，忽略了样本中无标签数据所包含的信息，半监督分类器并没有学习到原数据的总体分布。

针对以上问题，本文通过将WAE与半监督学习问题相结合，提出基于Wasserstein自编码器改进的半监督分类模型(WCVAE)，从边际分布出发，采用新的分布间距离度量，弥补常用分布间距离度量(如KL散度和JS散度)的缺陷，设置新的优化目标，不仅考虑有标签样本和无标签样本特征空间的边际分布和总体的边际分布相似，也考虑有标签样本的分布和总体的全概率分布相似，进而使得生成器能够学习到原数据的总体分布，降低模型的分类错误率，提高模型泛化能力。

2 WCVAE半监督分类模型

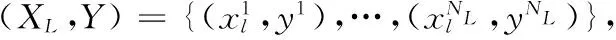
2.1 优化目标

数据的总体分布PA(x,y)由于无标签数据的存在，无法直接获得，但对于有标签数据，可以得到PL(xl,y)和关于xl的边际分布PL(xl)，同时，将半监督分类器所学到的分布，逼近全体数据的分布，即PC(y|xl)→PA(y|x)，并假设PA(x,y)和PL(xl,y)之间近似或者相同，当PA(x,y)分布和PL(xl,y)分布之间的Wasserstein距离越小，两个分布越相似，即有标签样本的分布和总体概率分布相似，如式(1)所示

(1)

式中：W为Wasserstein距离函数。

相比无监督生成模型VAE重构生成的是x，有监督生成模型CVAE在VAE的基础上，重构生成y|x，同时改进CVAE的变分下界损失函数，如式(2)所示

f(Qz,Pz;x,y)=-dKL(Qz‖Pz)+z～Q(Pz(y|x,z))

(2)

式中：dKL为KL散度度量，Qz是隐变量的近似分布，Pz是隐变量的先验分布，Pz(y|x,z)为生成模型，z～Q表示隐变量z服从Q分布的期望。

本文基于CVAE和WAE方法，将深度学习框架中的WAE生成模型改进成能够学习到原数据总体分布的条件生成器。训练好后，模型生成的数据的边际分布PGX(x)满足PGX(x)=PA(x)。同时，模型构造隐变量空间Z的近似条件分布Qz与先验分布Pz之间距离的惩罚项来放松模型中z的约束。WAE目标函数根据Wasserstein距离的原始定义进行推导，如式(3)所示

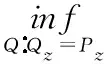
(3)

式中：P(x～PX,y～PGX)表示真实数据分布PX和生成数据分布PGX这两个边际概率分布组成的所有联合概率分布的集合。对于集合中的每一个可能的联合概率分布Γ，都可以从中得到一组样本(x,y)～Γ，c(x,y)是计算样本之间距离的任意成本函数，使用c(x,y)计算样本之间的距离。同时规定将所有联合概率分布的距离期望的下界定义为Wasserstein距离。

当PGX(x)=PA(x)时，即有标签样本和无标签样本特征空间的边际分布和总体的边际分布相似，优化目标如式(4)所示

(4)

式中：G(z)表示生成模型生成的数据，dz是测量Qz和Pz的任意散度，并且λ>0是一个超参数。

2.2 模型框架

针对上述优化目标，本文提出将WAE与半监督学习框架相结合，同时加入GAN中的鉴别器。主体包括：生成模型WCVAE，鉴别器D，分类器C，其中编码器E和生成器G构成生成模型WCVAE。模型框架展示如图1所示。

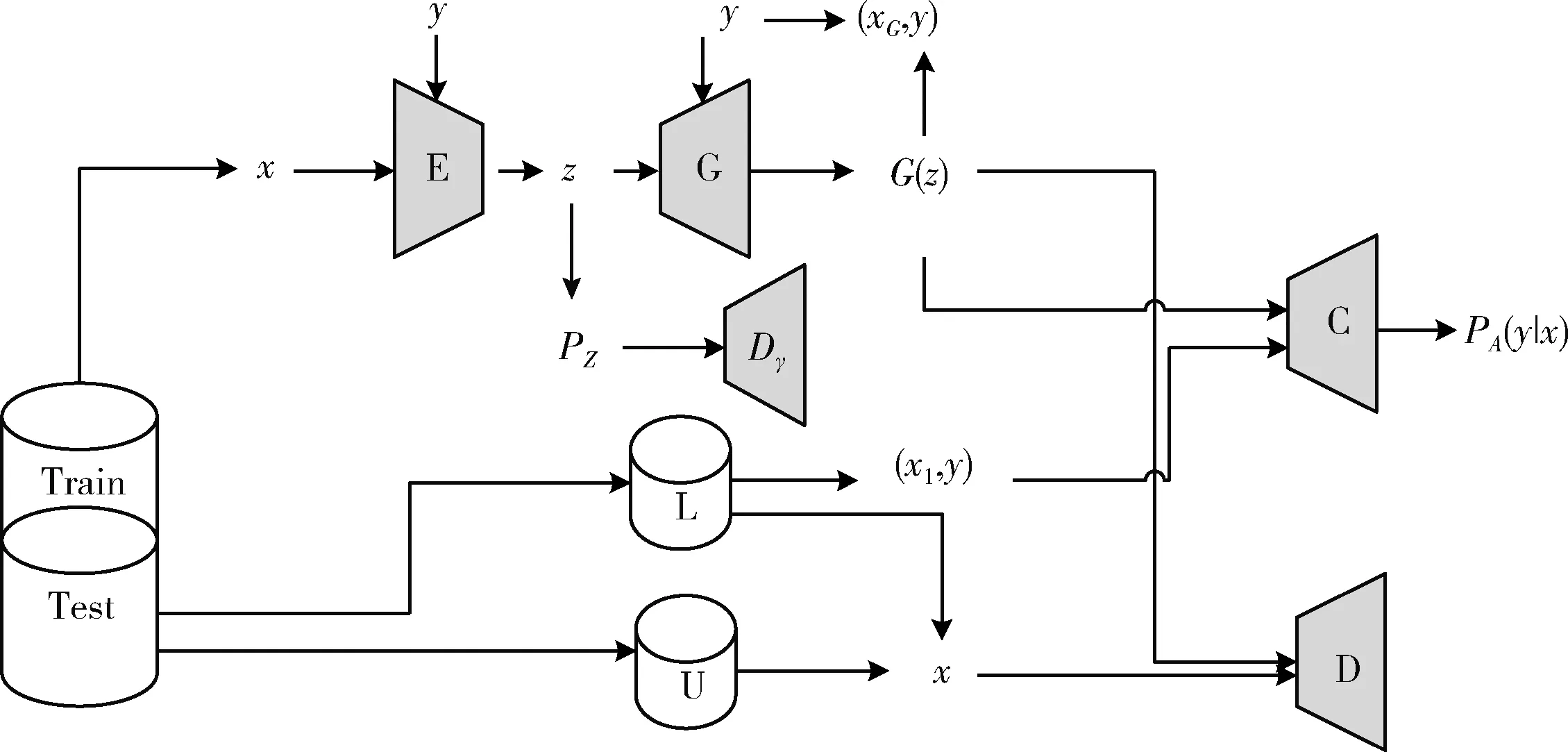
图1 WCVAE架构

图1中左上角E为编码器，由卷积层构成，该部件将样本映射到低维空间的隐变量z。G为生成器，由上采样层和卷积层构成，生成器将隐变量z还原成重构样本。图1右半部分D为鉴别器，由全连接层构成，鉴别器区分数据的“真”“假”。C为分类器，由卷积层和全连接层构成。图1中间部件Dγ为特征空间鉴别器，采用全连接层构建。

真实数据x从训练数据集采样，从编码器E左边进入，得到隐变量z，由生成器G生成新的数据G(z)，并将新数据传入鉴别器D中。为了提高模型生成的数据质量，本文在模型中加入鉴别器D，如图1右下角，模型中的鉴别器D和传统的半监督GAN类似，用来判断数据是“真数据”还是生成模型生成的“假数据”，同时和生成器进行对抗，两者共同成长，进一步提高生成模型生成样本的质量。因此，标签信息不会被应用到D中，真实的训练数据和生成器生成的“假数据”会在D中被区分出来。D的目标函数如式(5)所示

G(z)～PGX(z)[1-D(G(z))]

(5)

通过WGAN的结论，可以推导得到式(6)

W(PA(x),PGX(G(z)))=

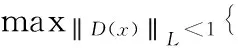
(6)

式中：L为利普希茨函数。

当模型的鉴别器达到最优时，将优化目标的结果转化为真实数据边际分布和生成器G的生成数据边际分布之间的Wasserstein距离,同时训练生成器G。本模型中的生成器G考虑有标签样本和无标签样本特征空间的边际分布与总体的边际分布相似。

生成器G的优化目标如式(7)所示

(7)

式中：λ·dz(Qz,Pz)类似VAE的正则项。同时考虑WAE中推出的基于GAN对抗方法的WAE-GAN，本文对该正则项方法加以改进。

WAE-GAN中dz采用对抗性训练来估计，使得dz(Qz,Pz)=dJS(Qz,Pz)。原文在隐变量空间Z中额外引入一个对手和新的鉴别器Dγ(如图1中Dγ部件)，试图将“假点”从Qz中分离出，将“真点”从Pz中分离出。同时也将对手从输入空间移动到隐变量空间，Pz相对于高斯先验分布将会有一个很好的单一模式的形状，并且相比匹配未知、复杂、多模式的分布会更容易。

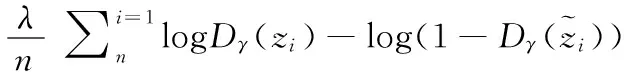
(8)

当鉴别器D和分类器C达到最优时，最终生成器的优化目标如式(9)所示

(9)

当生成器G达到最优，采用生成器G训练模型的分类器C。模型的分类器C将xl和G(z)作为输入，输出一个k维向量，同时采用softmax函数将其转换为类概率。每个类的输出代表后验概率PC(y|xl)。在训练阶段，分类器C试图最大化正确分类的概率，分类器C优化目标如式(10)所示

fC=-x～PL(xl,y)log[P(y|xl)]

(10)

最终可以得到模型优化目标，如式(11)所示

(11)

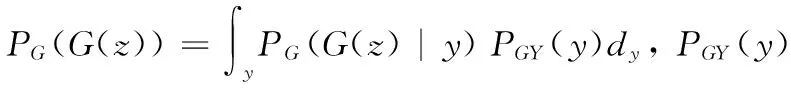
最终WCVAE模型训练过程如算法1所示。

算法1：基于WCVAE的半监督分类模型

输出：条件生成器G，分类器C。

while(W(PA(x),PGX(x)),θG)未收敛do：

从训练集中采用得到(x,y)，从高斯分布中采样得到(z1,…,zN)

fori=1 to n:

从后验分布Q∅中采样得(z′1,…,z′N)

endfor

使用式(8)更新Dγ

生成器G输出G(z)，训练鉴别器D：

fD=-log(D(x))-log(1-D(G(z′)))

训练生成器G：

训练分类器C：fC=-log(P(y|x))

endwhile

3 实验与分析

实验使用MINST[15]基准数据集，同时与半监督VAE算法M1+M2、ADGM、SeGMA[15]、针对错误率进行比较，以验证算法改进的有效性，并与基于GAN半监督深度学习算法CatGAN做进一步比较。

3.1 数据集及预处理

实验数据集采用MINST数据集，MINST是一个手写数字数据集，其中训练集有60 000张28×28图片，测试集有10 000张图片，每张图片的标签为0～9这10个数字其中之一。图2为MINST数据集部分样本。

图2 MINST数据集部分图像样本

本文采用MINST数据集中已有的划分，训练数据集采用全部的60 000个训练样本，训练600轮，每轮进行500批次训练。训练阶段，在训练数据集中随机抽取100个样本并对应标签，拼接成100个带标签样本，每批次训练数据集中包含100个标签样本和100个随机从训练集中抽取的无标签样本。测试阶段，本文从测试数据集中随机抽取100个测试样本，并随机生成0～9的10个数字其中之一作为标签输入。

3.2 实验设置

本实验在GPU服务器环境配备NVIDA Tesla P40和Ubuntu20上，使用Python3.8和深度学习开源框架Pytorch编码实现。

基于WAE改进的半监督深度分类模型中生成模型部分由编码器E和解码器G构成。模型采用Adam优化器，损失函数由反向传播算法进行更新,并且设定初始的学习率为0.0004,在最终阶段会线性下降到0，每一个批次的大小默认为100，同时采用ALM算法确定模型的超参数：鉴别器参数λ1、隐变量正则化系数λ2，同时更新潜在鉴别器参数Dγ。具体超参数设置见表1。

表1 实验超参数设置

为了定量评估半监督模型分类错误率性,本文基于MINST数据集进行对比实验。本文使用错误率作为评估标准,错误率越低，效果越好，具体计算公式如式(12)所示

(12)

式中：TP表示正例被模型判定为正类的数量，FP表示负样本被模型判定为正类的样本数量。

3.3 实验结果及分析

(1)与半监督VAE算法比较：本文将提出的方法在MINST数据集上与M1+M2、ADGM、SeGMA这3个半监督VAE算法进行比较，默认基于100个带标签样本。表2中前3行数据展示了3个半监督VAE算法基于MNIST数据集的错误率。从表2中可以看出，在与M1+M2、ADGM和SeGMA相比之中，三者的指标均高于本文推出的WCVAE算法，WCVAE与三者相比具有更好的质量，验证了WCVAE算法能够较好学习到原数据的全体分布。同时，相比于M1+M2算法会出现后验崩溃的情况，WCVAE具有更好的鲁棒性。

(2)与半监督GAN算法比较：从表2中可以看出，与CatGAN相比，WCVAE的分类错误率较为劣势，GAN模型在训练过程中容易出现不稳定和难收敛问题，CatGAN模型针对该缺点进行改进。WCVAE虽然采用了鉴别器D与生成器G进行对抗，但由于在特征空间加入鉴别器，同时采用Wasserstein距离进行改进，并未出现该问题，表明WCVAE的质量更好。模型损失曲线如图3所示(其中纵轴为比例值，故不带单位，横轴为训练轮次)，图3(a)为WCVAE模型损失曲线，图中虚线为模型生成器G的loss曲线，实线为模型鉴别器D的loss曲线，可以看到当达到20 epoch时，生成器G和鉴别器D已经趋于收敛，生成器虽略有波动，但后续也趋于稳定状态。图3(b)为CatGAN损失曲线，虚线为生成器loss曲线，实线为鉴别器loss曲线，当训练达到20 epoch时，鉴别器和生成器仍未趋于稳定，并处于波动状态，相比CatGAN训练后期阶段会出现难收敛现象，WCVAE具有更好的稳定性能。

图3 WCVAE(a)与CatGAN(b)损失曲线对比

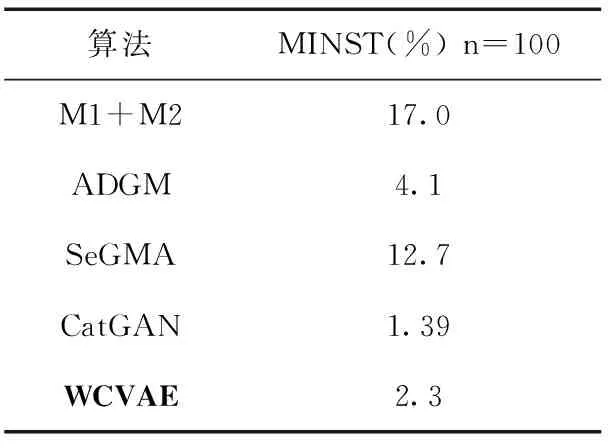
表2 基于MINST数据集的错误率

(3)不同标签样本数量对比：本文在MNIST数据集上采用20，50和200个带标签样本对算法进行评估。如表3所示，虽然在带标签样本数量为50和200的数据集中相比Improved-GAN错误率较高，但在带标签样本数量为20的数据集中，WCVAE算法具有更好的性能。经分析，WCVAE相比Improved-GAN能够更好学习到无标签样本和有标签样本的潜在信息，即WCVAE能12够真实学习到无标签数据和有标签数据的边际分布，并能够训练分类器学习到总体的分布。

表3 基于MINST数据集不同标签样本数量的错误率比较

4 结束语

本文针对当前基于VAE深度生成模型的半监督分类算法中忽略了样本中无标签数据所包含的信息，未能很好学习到逼近总体分布的问题，将WAE与半监督学习结合，提出基于WAE生成模型的半监督分类算法WCVAE，该算法优化目标既考虑了有标签和无标签样本特征空间的边际分布和总体边际分布相似，也考虑了标签样本分布和总体的全概率分布相似，同时采用Wasserstein度量替换VAE中原有的KL距离度量，使得生成模型能够学习到更加复杂的高维分布，进而使得半监督分类器能够学习到原数据的全体分布。实验结果表明，本文提出的模型相较于其它基于VAE深度生成模型的半监督分类算法具有更好的质量。