全景式数学教育视角下的“比较”： 从离散到连续,知结构而见森林

卢红旭

【摘 要】全景式数学教育强调“在整座原始森林中认识一棵树”，在该理念指导下，基于深度教材分析和认知心理学探讨“比较”单元结构化教学。对不同类型比较，借助非标准计量单位以一一对应比多少为线索建立联系，从离散的单位走向连续的物体，渗透“单位”概念，突出比较的本质，使学生在掌握比较方法的同时从整体视角认识比较，既见树木又见森林，明晰知识结构，实现全景式的数学学习。

【关键词】全景式数学教育 认知心理学 比较 非标准计量单位 一一对应

“不论我们选教什么学科，务必使学生理解该学科的基本结构。”理解学科结构依赖于课堂教学，伍春兰教授在系统观视域下提出，课堂教学结构是一个多种规律和谐发展的整体。但在传统教学中，各课时多呈现独立的状态，没有对知识点进行整合，长此以往，知识在学生脑海中成了一座座“孤岛”，不利于迁移运用。

全景式数学教育主张：让学生能更完整、更全面、更深刻地认识和思考数学本身及它所处的世界，基于课程标准和多个版本教材，以心理学和认知科学为依据，通过转变课堂教学结构有意识地体现知识结构，以使学生在看到一棵棵“树木”的同时发现整片“森林”。

本文以人教版数学一年级上册“比较”单元为例介绍全景式数学教育视角下的结构化教学。学生虽刚开始接受正式的数学教育，但已在有意识地寻找事物间的关联，发现物体间的异同点，初步具备了理解学科结构，进而完整、全面、深刻地认识数学与世界的认知基础。

一、分析教材，探究比较本质

《义务教育数学课程标准（2011年版）》仅对数的大小比较提出了明确要求，有关长度、面积等的比较则在附录中。大多数教材在一年级上册安排了比多少、比长短、比大小、比轻重等定性比较的内容，这为后续定量比较奠定了经验基础。

北师大版教材中先后比较了可数物体和不可数物体的多少。比较可数物体的多少比的是数量，“一一对应”是非常基础且重要的思想方法;对于液体这一不可数物体，比多少时比的是体积，常要借助某种容器。不同容器形状大小不一，若无法直接判断，可将其分别倒入同规格的小容器，此时小容器的容积为“单位体积”，能装满的小容器越多说明液体所包含的单位体积越多，其体积越大。

对于比长短，常用方法是将物体一端对齐，拉直后看另一端。若将比较对象按单位长度做标记，则可通过比较它们所含单位长度的个数来比长短，这就回归到了比多少。因此，所有的比较本质上都是在比较物体所含相同单位个数的多少，理论上都能用一一对应解决。此处的“单位”是非标准的，但其思想内涵与标准计量单位无异，所对应的心理图式基本一致。

鉴于此，以非标准计量单位为线索建立不同类型比较之间的联系，化离散的比较类型为整体的比较系统，呈现知识结构，通过顺应建立新图式，并在后续学习中通过同化对图式进行深化、完善。

二、建立联系，整合比较教学

（一）预——追本溯源寻内涵

教学片段：

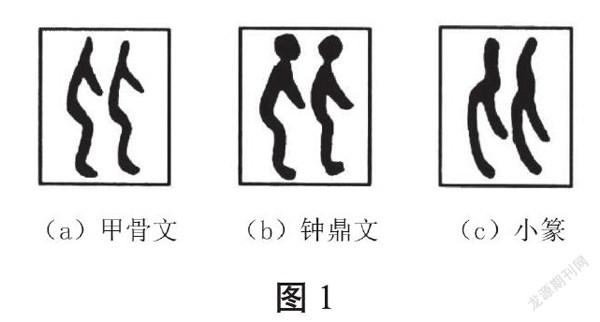
出示图1（a）-（c）。

师：认真观察各图，你们发现了什么？

生：第二幅图里的头最大。

生：两个人长得差不多，就差一点。

师：差在哪了？

生：个子！前两幅图中左边的人更高，第三幅图中右边的人更高。

师：你观察得真仔细！他们俩还有不一样的地方吗？

生：第二幅图中俩人的腿不一样，右边人的腿没怎么弯，左边人的腿弯得多。

生：第三幅图中他们的腰也不一样！左边人的腰很弯，右边人的腰更直。

师：这三幅图是同一个字，你们知道是什么字吗？（学生摇头）

出示图1（d）和（e），学生发现是“比”。

师：没错，就是“比”。当看到两个人在一起或者两样物品放在一起时，我们能发现他们有一样的地方，也有不一样的地方，这就是在“比较”。

【分析与说明】字源分析有助于学生理解概念。“比”是会意字，早期字形似两个人紧靠相依，并肩向前，本义为“亲近、紧靠”，引申为“并列、挨着、接近”。学生基于字形亲历比较过程，深刻体会其内涵，教师总结进一步明晰概念，學生初步建构“比较”的图式。

（二）起——一一对应破错觉

教学片段：

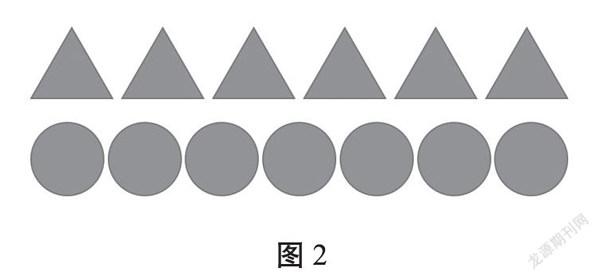
用磁贴呈现图2：

师：谁多谁少？

生：一样多！因为它们都是一个接一个，两边是齐的。

生：圆多，因为三角形是6个，圆是7个。

师：想象自己是一个原始人，不会数数，怎样知道谁多谁少？

生：对！

师：怎么“对”？

生上前操作得到图3：

师：为什么这样“对”能看出圆多，开始那样两边对齐就看不出来呢？

生：因为中间没对齐！两边齐了，可三角形更“胖”，所以放得少！

师：如果三角形和圆离得很远，用眼睛对齐很费劲怎么办？

生：用线连！

师：谁能给这种方法起个名字？

生：一对一！

生：连线法！

生：对应法！

师：数学上，把这种一个对一个的方法叫“一一对应”。

【分析与说明】一一对应比多少是感悟比较本质的重要过程，故最先呈现。根据皮亚杰认知发展阶段理论，学生处于前运算阶段向具体运算阶段过渡的时期，对比较的认知多处在生活概念层次，在比较某一属性时易受其他属性的干扰。课上“一样多”的错觉引发了学生的认知冲突，打破了平衡状态，激发了学生的学习热情。学生多通过数数来比较，原始人的设定迫使其另寻他法。学生“经历”知识产生的过程，回归最原始、最根本的“一一对应”，为方法起名字加深了对“一一对应”的理解，其认知重获平衡，比较的图式得以丰富。

（三）承——标准清晰言多少

教学片段：

师：只说“圆多”准不准确？

生：不准确，得说“多多少”。

师：多多少？谁能说完整？

生：圆多1个。

师：如果还有正方形呢？（在图上补5个正方形）和正方形比，圆还是多1个吗？

生：2个。

师：怎么一会儿多1个一会儿多2个？

生：和三角形比多1个，和正方形比多2个！

师：和谁比，谁就是标准，说比较结果时要把标准也说出来。

【分析与说明】比较具有相对性，正方形的引入搅动了学生的认知结构，他们在寻找平衡的过程中感悟标准的重要性，对比较的要素有了更清晰的认识。

（四）转——变换角度比长短

教学片段：

出示散乱摆放的小棒，其中橙色5根，绿色7根，学生一一对应比较二者多少。将小棒横向连接如图4：

师：哪条长？哪条短？为什么？

生：下面的长，上面的短，因为一一对应后，下面多2根。

生：我发现小棒越多，连的线越长。

师：你说越多越长，可是两根小粉笔头接起来都没有完整的粉笔长呀！

生：因为小粉笔头太短了，加起来也很短。

师：什么时候会越多越长？

生：如果每根粉笔一样长，就越多越长了。

师：如果每段一样长，就越多越长。这样的一段就是一个单位，谁的单位多谁就长。

【分析与说明】根据认知发展阶段理论，学生对量的守恒已有一定的感知。由于刚学了一一对应比多少，因此将小棒横向连接后（小棒本身没变），学生自然而然地将一一对应迁移到了比长短中，在两种比较间建立了联系。比较粉笔的长短这一反例的呈现挑战了已有的心理图式，促使学生寻找“段数越多就越长”的前提——单位长度相同。

生：要是看不出来谁的单位多怎么办？

生：可以画出来，数一数。

生：画得不一样长怎么办？

生：用尺子！那上面的格子一样大！

师：没有尺子怎么办？能不能直接比？比如：这两根粉笔怎样比长短？

生：把一头对齐，看另一头就行了。

师：（拿出两团绳子）怎样比较两团绳子的长短？

学生操作，总结比较绳子长短的步骤：一端对齐;拉直;看另一端。

师：为什么这里是三步，而在比粉笔的长短时只有两步？

生：因为粉笔就是直的呀！

之后比高矮环节，学生惊奇地发现比高矮和比长短的过程是一样的！如此，将这两“点”连成了“线”。

【分析与说明】很多时候通过比多少来比长短并不方便，因此需要探寻比长短的一般方法，这对已具有一定生活经验的学生来说并非难事。比身高丰富了比长短的内涵，加深了学生的理解。

（五）合——打通维度现结构

比轻重和比大小的教学思路与比长短的教学思路相同，比较对象由单位立方体组成，既可以从单位的角度一一对应比较，也可以整体进行比较。

最后，对不同类型的比较进行了回顾，学生进一步体会到一一对应可用于多种类型比较，虽然有时不方便，却是一种普适的思想方法。（如图5）

传统教学通常逐一探讨不同类型的比较，缺乏连续性，学生不断“转场”，流连其中，“只见树木，不见森林”，缺乏顶层思考。一一對应是比较的基本思想方法，以一一对应比多少为线索串联不同类型比较，有助于学生构建知识结构。先比较离散的单位的数量，再对由离散单位所组成的连续物体进行比较，渗透“单位”概念的同时突出比较的本质——比较物体所含相同单位个数的多少。最后的整体回顾使学生在掌握具体比较方法的同时能从整体视角认识比较，既见树木又见森林，形成完整的知识框架，促进深度理解。

三、回顾反思，总结比较教学

以一一对应比多少联结不同类型比较是在利用非标准计量单位进行定量比较，学生对此有一定体会，并能采取合适的方法正确比较。全景式数学教育通过跨单元、跨领域、跨学科乃至学段的整合使学生能用更广阔的视角发现当下的学习并看见其未来，走好每一步。

对于“比较”，还可以从以下两方面进行探索：

（1）关注比较的现实价值。乌申斯基说过：“比较是一切理解和思维的基础，我们正是通过比较来了解世界上的一切的。”然而，教材上的问题几乎只要求得到比较结果就可以，脱离了现实情境。得到结果不是终点，在日常生活中应引导学生思考如何应用比较结果。

（2）拓展比较对象及维度。教材中的比较对象和比较维度很有限，我们完全可以扩展到更大的范围，如比较两棵树的粗细、比较两种事物保质期的长短、比较两种声音的高低强弱等，这样学生会对“比较”有更系统、完整、全面的认识。