基于k -fold交叉验证的代理模型序列采样方法
李正良, 彭思思, 王 涛*
(1.重庆大学 土木工程学院,重庆 400045;2.重庆大学 山地城镇建设与新技术教育部重点实验室,重庆 400045)
1 引 言
对于一些较为复杂的实际工程问题,常采用物理实验和仿真模拟进行深入探究和分析,但这些方法往往需要消耗大量的人力物力,耗时长,成本高,其应用受到很大限制。而代理模型技术可以有效解决上述问题,成为一种非常流行的代替昂贵数值模拟的有效方式[1]。代理模型的本质是用输入和输出参数来模拟响应系统的行为,通过选取一定数量的样本点来构建具有相当精度的数学函数模型,其在工程设计和优化中得到广泛应用[1]。作为构建代理模型的关键步骤,采样方法至关重要,采样方法选取的样本点很大程度地决定了代理模型的精度水平。如何选取尽可能少的样本点构建具有足够精度的代理模型一直是研究者们关注的重点和热点,对此国内外学者展开了大量的研究[1]。
现有的代理模型采样方法一般分为一次性采样方法和序列采样方法两大类。一次性采样(one -shot sampling)方法主要考虑空间填充设计,使样本点尽量均匀地分布在整个设计空间中,较为常见的方法有全因子试验设计法、正交设计法和拉丁超立方采样法等[2]。然而在实际工程中采样数量往往难以确定,一次性采样容易导致过采样或欠采样[2],造成计算资源的浪费或近似精度难以满足要求,且自适应能力差。相较于一次性采样方法,序列采样方法(sequential sampling)对初始样本的依赖性较弱,能有效控制样本的数量,可以根据实际物理系统的空间特性进行采样,因此得到了学者们的青睐[3-7]。序列采样方法的基本思路为选取少量样本初步构建近似模型,在序列迭代的过程中充分利用已有样本和模型的信息来确定候选样本点的位置,通过在欠采样和高度非线性的局部区域逐步加点,不断提高模型的近似精度,直至满足设计者的需求。当前,该方法已应用于模型预测[3,4]、优化设计[5,6]以及可靠度分析[7]等诸多领域。
为了在整个设计空间中得到良好的全局近似结果,兼顾代理模型的全局精度和局部精度,不少学者针对全局代理模型的序列采样方法进行了深入探究。其中,泰森多边形(或Voronoi)作为一种合理划分空间和分析影响区域的常用工具,能有效地对整个设计空间进行全局探索,近些年来应用于序列采样方法的相关研究中。Crombecq等[2]提出了一种LOLA-Voronoi序列采样方法,创新性地根据泰森多边形法衡量样本密度,并通过局部线性逼近法分析数据点周围的非线性程度,进而选择新的候选样本点。但该方法在估计样本的梯度信息时需进行复杂的邻域选择,计算速度较慢;Xu等[8]结合了泰森多边形法和LOO交叉验证(leave -one -out cross validation)误差进行采样,发展了一类鲁棒性强的CV-Voronoi序列采样方法;缪继华等[9]将CV-Voronoi方法与支持向量回归模型相结合,提出了基于支持向量点的空间加点策略。虽然CV-Voronoi序列采样方法具有较高的精度和较强的鲁棒性,但其序列采样过程中交叉验证涉及大量的建模计算,且随着样本点数量的增加,计算量不断上升,致使其计算成本较为昂贵。
鉴于此,为了节约计算成本、加快采样速度及提高建模效率,本文引入k-fold交叉验证(k-fold cross validation)[10]方法,并结合泰森多边形法对设计空间进行全局探索和局部开发,发展了一种k-fold CV-Voronoi自适应序列采样方法,并通过数值算例和工程算例对本文方法进行验证。
2 序列采样方法
2.1 k -fold CV-Voronoi序列采样方法
本文发展的k-fold CV-Voronoi自适应序列采样方法基于泰森多边形法剖分设计空间,通过k-fold交叉验证方法展开误差追踪,在交叉验证误差最大的区域内进行自适应采样。该方法核心内容包括剖分设计空间、确定子区域以及选取候选点。
(1) 设计空间剖分。泰森多边形由离散点连成的三角形各条边的垂直平分线围成,是对空间区域的一种无缝不重叠剖分。对于d维设计空间Ω的一组样本点X={x1,x2,…,xn},其中第i个点xi的Voronoi区域Di定义为[9]
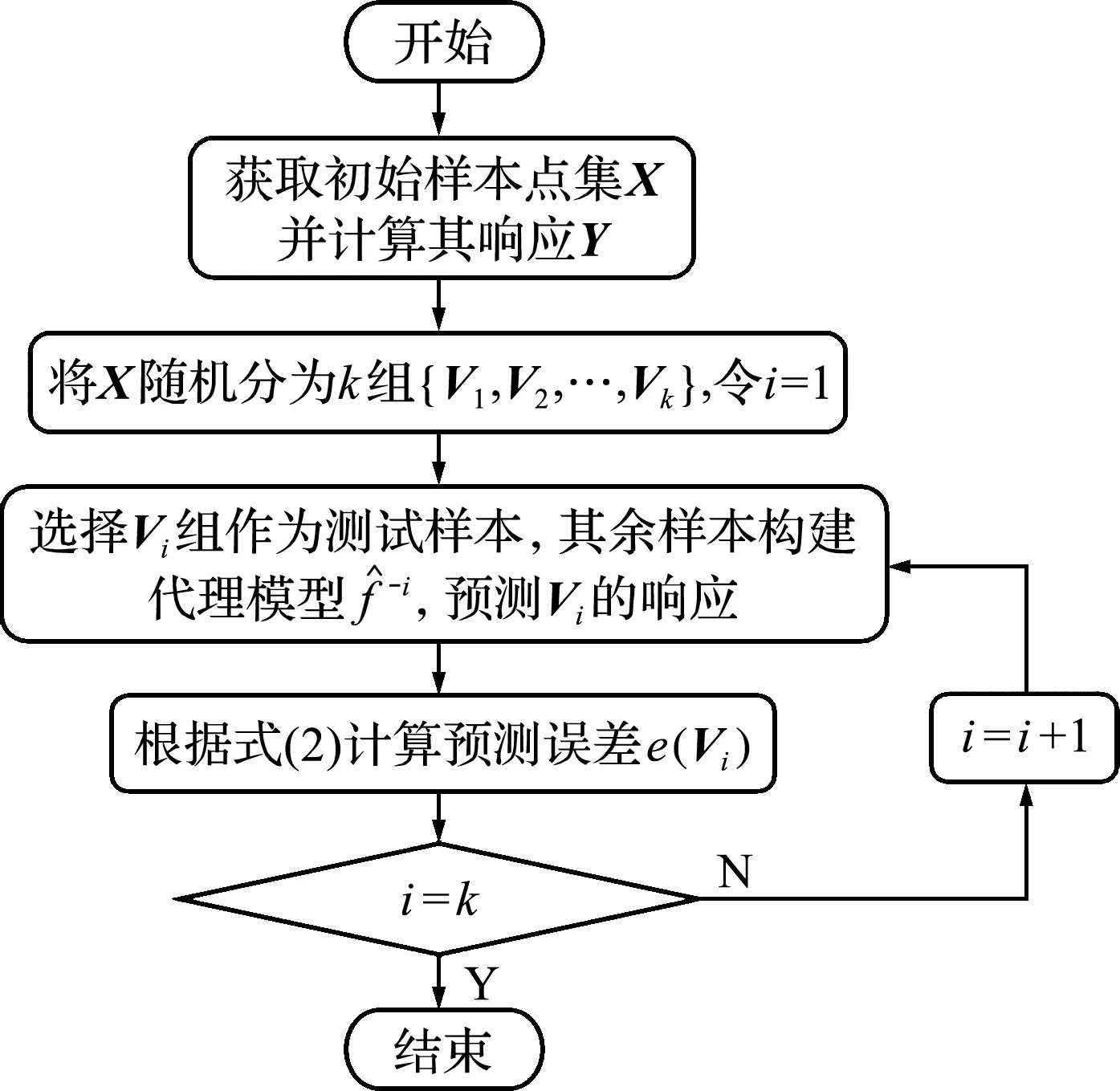
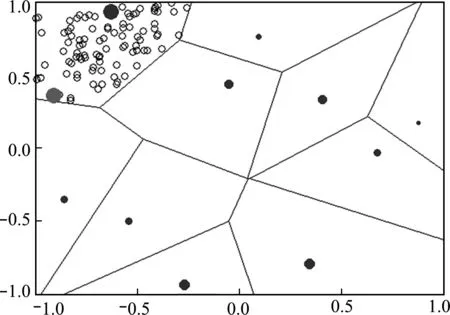
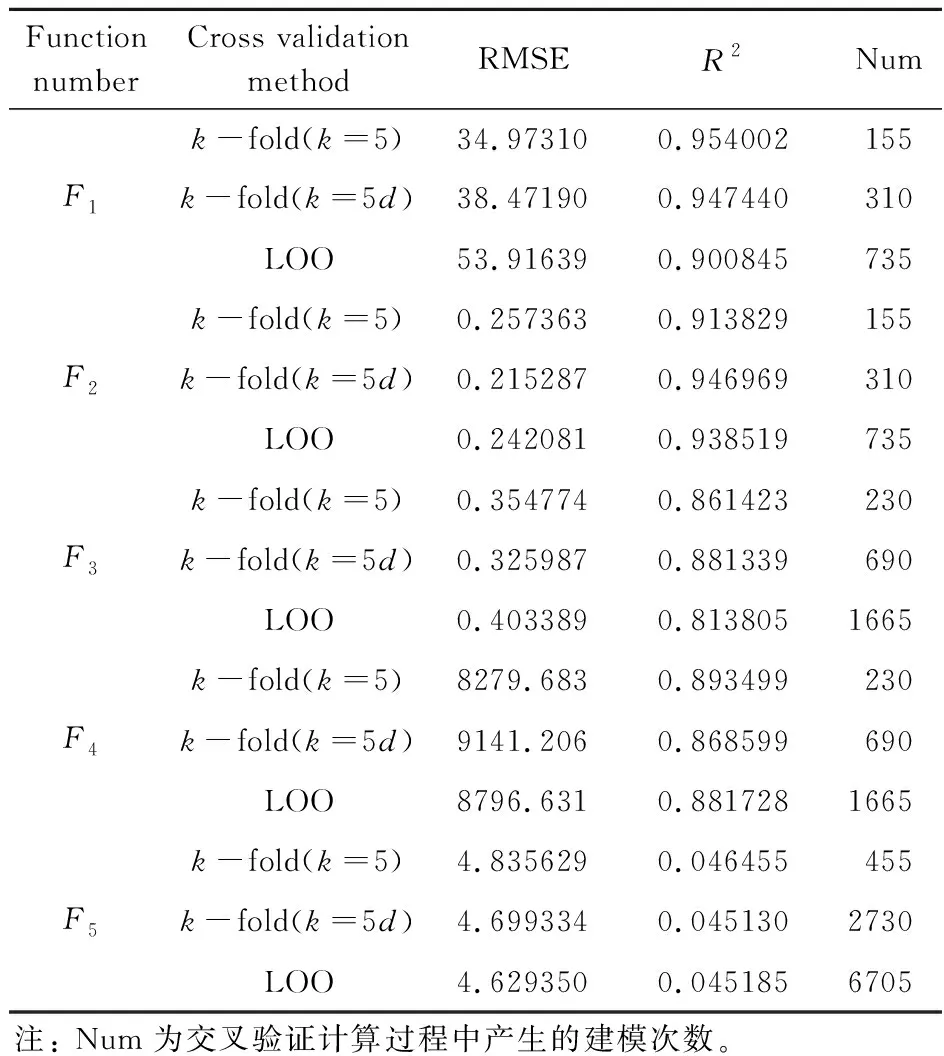
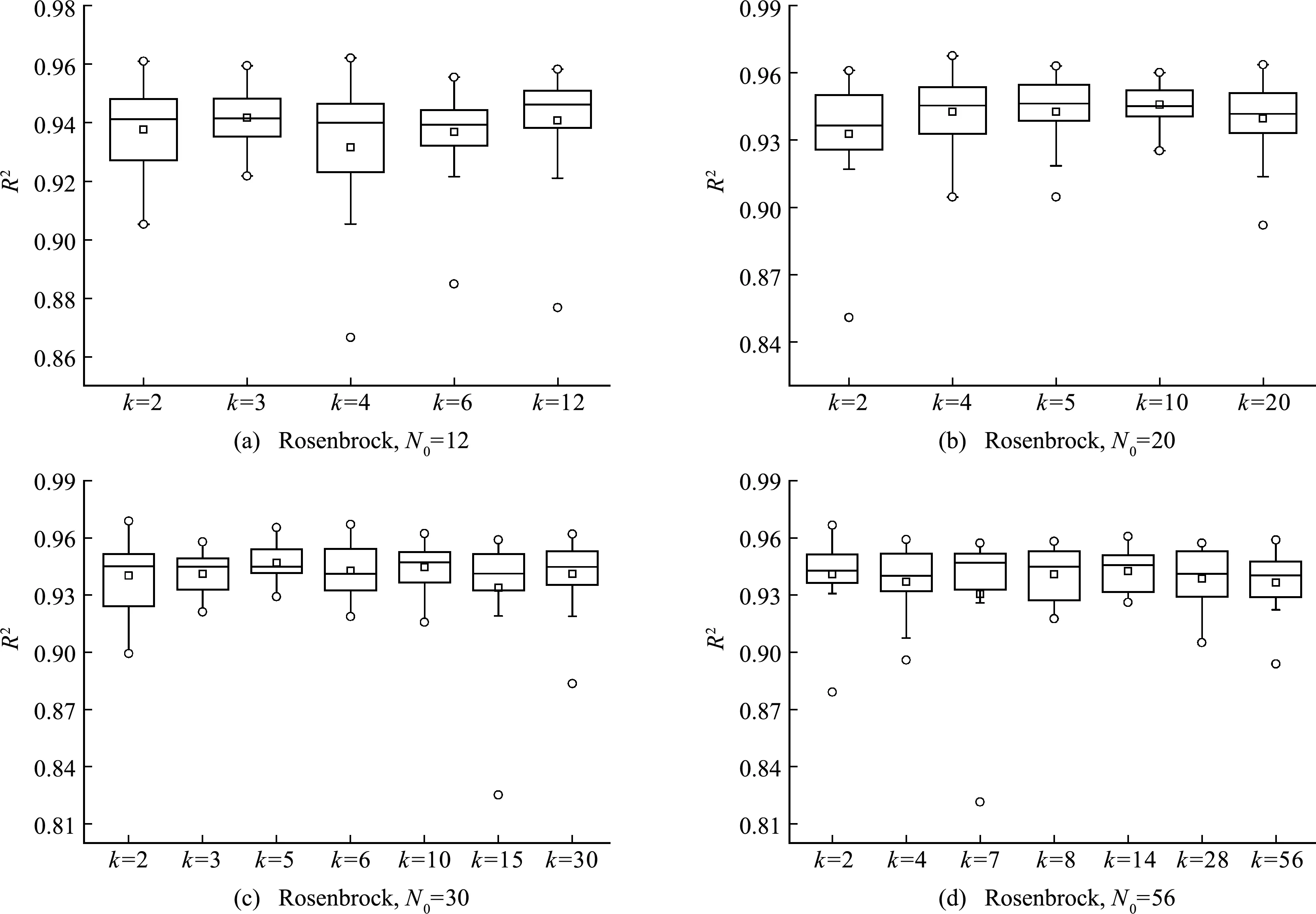
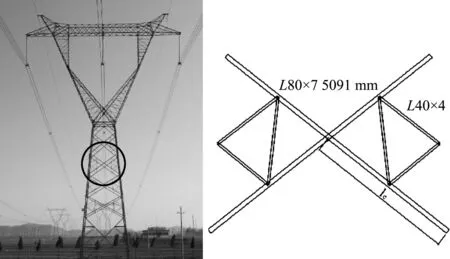
Di={x∈Ω|d(x,xi) (j=(1,2,…,n),j≠i) (1) 式中n为已知的样本数量,x为设计空间Ω的向量点,d(xi,xj)为样本点xi和xj之间的距离。 以二维设计空间为例,在[-1,1]2范围内随机生成10个样本点,其Voronoi单元划分情况如 图1 所示。可以看出,任意一个泰森多边形Di内部只存在一个已知样本点xi,且多边形Di中的点与其中心样本xi的距离最近,因此可将多边形Di围成的区域视为样本xi的有效影响范围。 图1 二维Voronoi图及其单元预测误差 (2) 子区域确定。当整个设计空间划分为一系列多边形区域后,需进一步考虑代理模型在各个子区域内的近似情况,在预测误差较大的区域增加样本点能有效提高模型精度。交叉验证方法可以获取样本点的预测误差信息,可用于评价代理模型的近似效果,但常见的LOO交叉验证方法随着序列采样过程的进行,所需的计算量在成倍上升,计算成本较大。因此,本文引入k-fold交叉验证方法[10]计算样本点的预测误差,其详细步骤如图2所示。 图2 k -fold交叉验证方法流程 k-fold交叉验证方法将样本集X随机分成k组(k≤n)互斥的子集{V1,V2,…,Vk},分别计算各集合中样本点的预测误差[1],其表达式可写为 (i=1,2,…,k)(2) 图1所示的二维实例中,采用不同大小的实心圆点表示由式(2)计算的样本点预测误差值,当样本点xi的误差ei越大,即表明在多边形Di区域内代理模型的拟合效果越差,与实际函数存在较大偏差。假设第c个样本点xc的误差最大,在相应的多边形Dc区域内进行采样。 (3) 候选点选取。为保证样本的空间填充特性,最大程度获取函数局部信息,k-fold CV-Voronoi自适应序列采样法应满足多边形区域Dc内的候选样本点与其中心点xc之间的距离尽可能大。具体操作为在预测误差最大的多边形区域内产生一批随机点,根据式(3)所示的最大距离最小化(maxmin)准则[11]抽取新的样本点, max[d(x,xc)] (x∈Dc) (3) 式中max(·)为求最大值的函数,x为区域Dc的向量点。 对于二维空间,采用上述方法进行采样的结果如图3所示,其中空圆圈代表一系列随机点,实心点即为新增样本点。 图3 二维采样过程 与一般的序列采样方法对比,本文建议的k-fold CV-Voronoi自适应采样方法存在三点优势。其一,该采样方法本身完全独立于代理模型技术,因此能与多种类型的代理模型相结合,可应用于不同工程问题,具有普适性;其二,算法中包括探索阶段和开发阶段两个过程,通过泰森多边形的空间划分和交叉验证误差的计算,实现了整个设计空间内局部开发和全局探索之间的动态平衡,自适应性强;其三,引入k-fold交叉验证策略能有效减少建模过程的计算成本,加快采样速度,提高建模效率。 对于实际工程中的建模问题,采用k-fold CV-Voronoi自适应序列采样方法构建精确代理模型的具体步骤如下。 (1) 选取适当的试验设计方法,在设计空间中抽取少量初始样本集X,并计算其响应Y。 (2) 根据样本及其响应值,建立相应的代理模型,并计算模型的近似精度。 (3) 基于已有样本信息,利用泰森多边形法剖分整个设计空间。 (4) 采用k-fold交叉验证方法计算每个样本点的预测误差,选出误差最大的样本点所在的多边形区域。 (5) 在选出的多边形区域中产生一系列随机点,根据maxmin准则选择候选样本点xnew并计算真实响应值ynew,将其加入集合X和Y,更新样本。 (6) 检查停止准则。若计算结果满足给定的停止准则,建模结束;否则,继续步骤(2),进行下一轮迭代。 RBF是目前应用最为广泛的代理模型之一[12],其选择某一欧氏距离函数作为基函数,通过径向基函数的线性组合来拟合实际函数,所得模型近似精度比较高,具有良好的鲁棒性,适用于解决高度非线性问题[13]。为验证k-fold CV-Voronoi自适应序列采样方法的效率以及适用性,将建议的自适应序列采样方法与RBF代理模型相结合,应用于数学函数算例进行对比分析,并针对k-fold交叉验证方法中k的取值展开讨论。 将建议的k-fold CV-Voronoi自适应序列采样方法应用于5个典型的数学函数,建立RBF模型并检验其精度,并与Xu等[8]提出的基于LOO 交叉验证的CV-Voronoi采样方法进行对比。数学测试函数的相关信息列入表1。 表1 测试函数信息 为了获得尽可能多的函数信息,初始样本点应在整个设计空间中均匀分布,并且具有良好的投影特性,故本文采用操作简单和易于实现的拉丁超立方抽样法(LHS)[14]选取初始样本。在序列加点过程中,考虑有限的计算成本,设置停止准则为,循环加点过程中当生成的总样本达到设置的最大样本数量时停止采样。若测试函数的设计维度为d,设置初始样本数量为N0=5d,最大样本个数为N=4N0。抽取500个测试样本验证代理模型的精度,采用两个常见的模型全局精度指标评价模型的近似程度,均方根误差(RMSE)和平方相关系数(R2)的表达式为 (4) (5) 为了消除随机误差的影响,表2所列结果为多次计算的平均值。 表2 不同采样方法下RBF建模结果 由表2可知,在初始样本和总样本数量不变的条件下,本文方法所得能以少量的计算成本取得较好的建模效果,而LOO交叉验证策略下序列采样过程中的建模次数远高于k-fold交叉验证。设初始样本数量为N0,采样结束时的样本总量为N,采用LOO交叉误差验证的CV-Voronoi自适应序列加点方法共需要1/2(N+N0-1)(N-N0)次建模,而采用本文的k-fold CV-Voronoi方法仅需k(N-N0+1)次建模计算,大幅缩减了计算消耗。 另一方面,对比表2各个函数模型的精度指标发现,在计算成本较小的前提下,本文方法的精度水平不低于CV-Voronoi自适应序列加点方法。综合而言,本文方法计算成本低,计算效率高,且鲁棒性强。 值得注意的是,表2中代理模型的精度结果随本文方法k的取值变化而发生改变,因此,为了确定k值的取值,本文进一步探究不同k值对代理模型精度的影响。仍采用表1的函数为例,对于每个测试函数,分别选取了不同的初始样本值N0,其相应k值在N0的公因数按从小到大的顺序分别进行取值[16],如当初始样本个数N0=12时,k值分别取2,3,4,6和12,样本总量保持不变。采用本文方法建立RBF模型,以全局指标R2衡量模型精度,将多次测试结果整理成如图4所示的箱线图。 图4 不同k值情况下RBF模型精度 通过观察图4平均数、众数和分位数等数据发现,在初始样本数量相同的情况下,同一测试函数不同k值下所得代理模型计算结果均未表现出明显的线性规律,即当k发生变化时,RBF模型的整体精度R2可能上升亦可能下降,在局部区域会出现极值。根据试验中多种情况下所得测试结果可知,对于所有测试函数,当k/N0=1/6~1/3时,所得模型的精度较高,且一般在k=1/4*N0处取得极值,建模效果最佳(如图4中Rosenbrock函数在N0=12,k=3;N0=56,k=14时取得最优结果),并且此时交叉验证的次数较少,计算成本低。 文献[17,18]也对比了LOO和k-fold交叉验证,证明在一次性采样建模中k-fold交叉验证方法取k=10时取得较优结果。但采用序列采样方法构建代理模型时,可以通过不断添加新的样本来更新模型,在多次循环迭代过程中不断提高模型精度,常选用较小的初始样本值和k值,故在上述k-fold CV-Voronoi方法测试中,k的建议取值略小于以往文献给出的参考值。 图5所示的交叉斜材作为保证输电塔结构稳定性的重要部件,对承受横向荷载起着关键作用,并且常与辅材一起改善输电塔内部的结构受力。 图5 输电塔交叉斜材构造 交叉斜材的承载力与截面几何尺寸和拉压比等因素之间的函数关系是其设计与优化的关键。本文选取交叉斜材的角钢截面肢长l、肢宽b以及拉力与压力的比γ作为自变量,通过ANSYS有限元分析软件对输电塔交叉斜材进行数值模拟分析,计算不同参数下杆件的最大内应力响应,采用本文方法建立RBF模型。建模过程中初始样本数量为N0=15,测试样本数量为30,k-fold交叉验证的k值取为1/4N0。 表3展现了建模过程中随着样本数量N的增加,RBF模型精度的变化情况。由表3可知,本文方法能快速提高代理模型的近似程度,当样本总量为30时,代理模型的整体精度R2达到80%以上,能够以较小的计算成本取得令人满意的建模效果,且所得代理模型可进一步用于输电塔交叉斜材的设计和优化。在实际应用中,设计者可根据目标函数精度要求控制加点过程的进行,从而提高建模效率,节约了计算成本。 针对现有采样方法的不足之处,本文发展了一种适用于任意代理模型的k-fold CV-Voronoi自适应序列采样方法,该法能有效地在整个函数设计空间进行全局探索和局部开发,具有很强的自适应性和鲁棒性。通过数学算例和工程算例得结论如下。 (1) 相同条件下,本文方法在序列迭代过程中交叉验证的建模计算次数较低,能大幅减少计算成本,提高建模效率。 (2) 本文方法适用于复杂系统的建模分析,且在计算资源有限的情况下具有显著优势。 (3) 提供了本文方法中k值的最佳取值范围,即k=(1/6~1/3)N0,可供设计及科研人员参考。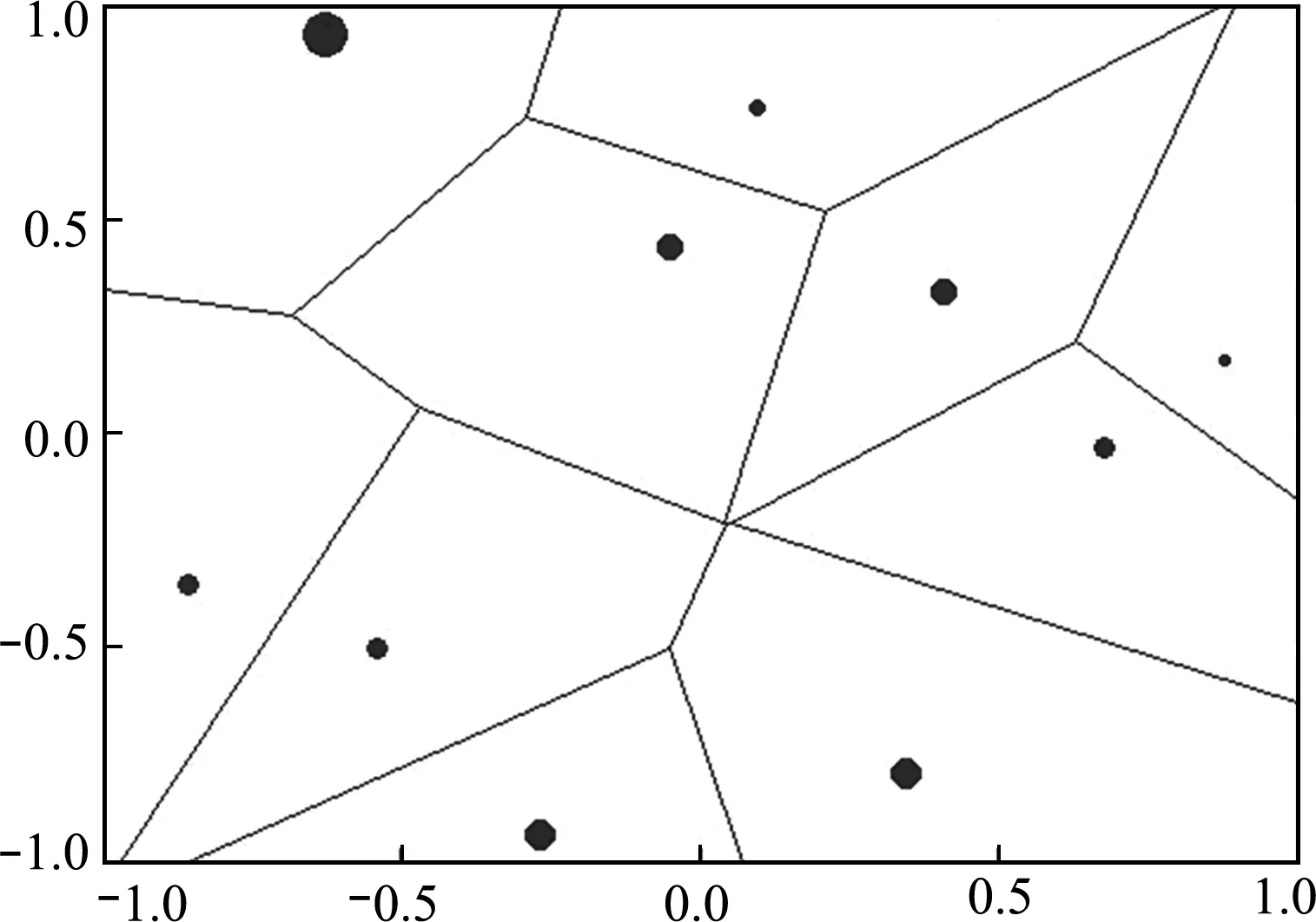
2.2 算法流程
3 数学算例
3.1 数学函数测试

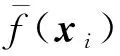
3.2 关于k的讨论
4 工程算例
5 结 论

