基于二次型性能指标定轴转动板减振拓扑优化
张君茹, 程耿东
(大连理工大学 工程力学系,大连 116024)
1 引 言
旋转结构在工业中有着广泛的应用,如涡轮发动机、直升机、风力发动机叶片和旋转太阳帆。当旋转结构工作时,可能会受到外界环境的干扰或者冲击,如异物撞击或者砂粒等[1,2],从而产生偏离正常运行的振动,影响旋转结构的正常功能,研究冲击荷载下的旋转结构减振问题是十分有必要的。
旋转结构动力学理论研究工作从研究旋转梁的动力学特性和响应起步,单杆机械臂或者叶片的结构分析和优化是以梁结构的研究为基础[3-5],但是梁结构不能很好地模拟具有低展弦比的结构,在很多应用中,研究旋转板的动力学特性和优化方法更合理必要。旋转板建模方法的主流方法有浮动坐标法和绝对节点法两类。基于浮动坐标法,文献[6,7]研究了旋转薄板的动力学响应和模态特性,Hashemi等[8]研究了旋转厚板的动力学响应和模态特性。赵将等[9]基于绝对节点法研究了旋转薄板的频率和模态特性,但是在处理斜率不连续问题时仍然需要进一步研究[10],优化设计过程中出现相邻单元密度不相等造成斜率不连续情况。本文采用浮动坐标法建立平面旋转板的多体动力学数学模型。
旋转板结构的减振优化设计和研究工作相对少见。刘利军等[11]研究了转动ACLD悬臂板的动力学建模及主动约束层阻尼层的振动控制。孙家亮等[12]基于移动可变形组件法(MMC)和绝对节点法(ANCF)研究了旋转薄板频率拓扑优化方法。
动力学减振优化的研究按照目标函数或者约束函数分为两类。一类是基于结构动力学特性如频率或者模态,这方面的工作很多;另一类是基于动力学响应。Kang等[13]综述了基于响应的优化工作,指出基于结构响应的优化问题需要求解每个时间积分步上的动力学响应,求解每个时间步响应的敏度十分耗费时间。基于动力学响应但不考虑每一个时刻的响应,赵君鹏等[14]提出基于响应的积分形式目标函数,阎琨等[15,16]使用积分形式的二次指标作为目标函数,使用李亚普洛夫方法将该指标简化,并使用伴随法计算该指标的敏度,求解了受冲击荷载板结构阻尼拓扑优化。
本文结合多体动力学理论和有限元方法推导了常速旋转板的面内振动动力学方程,并采用二次型性能指标作为目标函数,结合李亚普洛夫方法,建立以单元人工密度作为设计变量的SIMP(Solid Isotropic Material with Penalty)结构拓扑优化列式,研究在给定材料体积的条件下,受到冲击荷载作用的旋转板的拓扑优化减振设计。本文还讨论了以二次型性能指标和以基频为目标的优化设计的异同,发现在远端有环向支撑时,板基频最大的设计是重频率设计,但是,以二次型性能指标作为目标函数的优化设计没有重频。
2 垂直于旋转轴的平板动力学方程
2.1 浮动坐标法下广义位置坐标
考虑板以Z轴为旋转轴在平面内大范围转动,并假设发生的面内变形是小变形,使用平面应力板单元来离散板结构和模拟板的变形[8]。任取板中一点P,点P到板结构坐标系ObXbYb原点Ob的位置矢量为uP,点P到全局坐标系OXY原点O的位置矢量为r,点Ob在全局坐标系OXY的位置矢量为R,旋转板绕Zb轴旋转θ角,点P发生的变形为u。则P点全局位置矢量r表示为
r=R+T(uP+u)
(1)
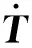
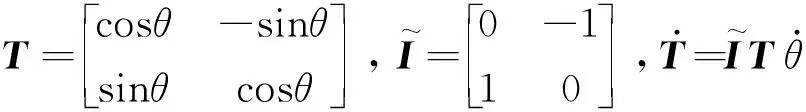
(2)
点P变形表示为
u=Nqe
(3)
式中平面应力板单元自由度qe和形函数N的表达式参见文献[17]。旋转板结构上任意点P的全局位置矢量r由广义位置坐标qP唯一确定表示
(4)
式中结构自由度q由单元自由度qe组集而成。
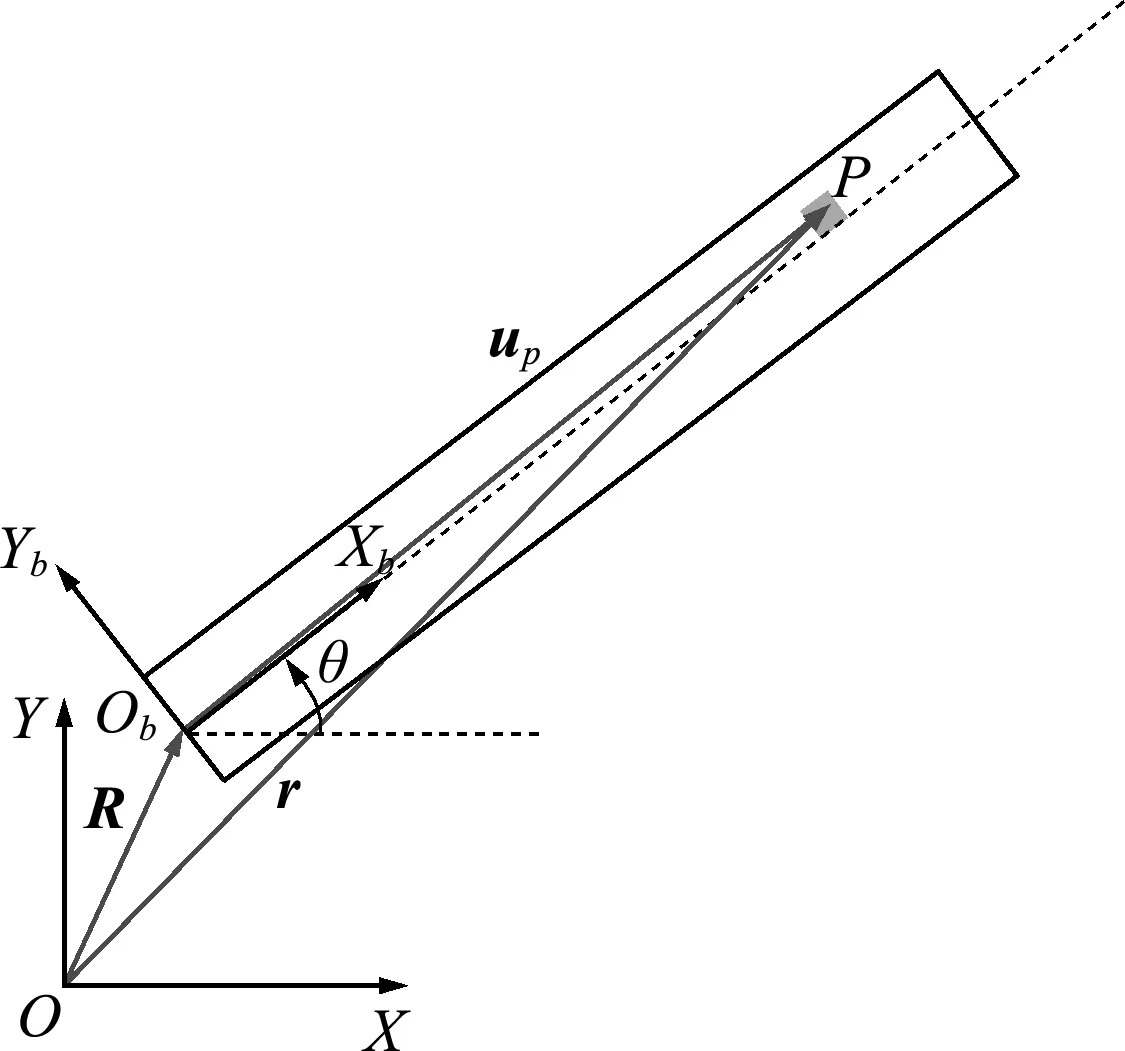
图1 板中任取点P的位置
2.2 旋转板的质量和刚度矩阵
点P速度由该点的位置矢量对时间求导得
(5)
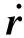
旋转板的动能和质量矩阵表示为
(6)
式中M(qP)为结构有限元模型的单元质量矩阵,其分量表达式参见文献[17]。
板的弹性势能和刚度矩阵可以表示为
(7)
式中应变矩阵B和弹性矩阵D参见文献[18]。
2.3 稳定旋转板受冲击扰动动力学方程
动力学问题的拉格朗日方程为
(8)
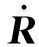
(9)
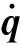
(10)
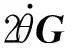
(i=1,2,…)
(11)
式中结构的阻尼比ξ是与材料的性质或者应力的状态有关的,一般在0.5%~15%之间[19]。本文采用α和β为 10和1e -5。使得对于本文算例,与基频相应的阻尼比落在此区间。
假定旋转板从初始启动后经过一段时间进入稳定旋转,转速ω为常数,在转动中设想受到外物碰撞、打击或者爆炸等作用时间极短的冲击,假设冲击后结构还处于未变形状态,并将冲击荷载简化为在板冲击点处施加冲击速度[20]。受到冲击稳定旋转板的扰动动力学方程可表示为
(12)
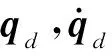
将式(12)转化为状态方程,可表示为
(13)
式中A为状态矩阵,x为由扰动速度和扰动位移组成的状态向量。
3 旋转板的减振拓扑优化
研究均匀厚度为h的旋转板的拓扑优化,待设计的板结构所在的设计域为Ω。假定板的材料性质和边界条件、允许使用的板的材料体积、冲击荷载的位置和大小以及观察点的位置与方向都已经给定。稳定旋转板在受冲击后发生振动,本文目的优化结构的拓扑以降低观察点的振动。
3.1 以二次型性能指标为目标的优化列式
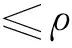
(14a)
(14b)
(14c)
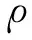
(e=1,2,…,n) (14d)

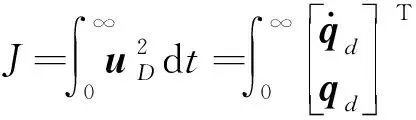
(15)
式中uD为人为选取受冲击板上观察点D在体坐标系下Yb方向的扰动位移,冲击点和观察点可以相同或者不同,算例1中观察点D的位置如图2所示。W为权系数矩阵,除了对角线上W(uD,uD)的值等于1,其余元素均等于0。在拓扑优化过程中,材料的密度分布在不断发生变化,为了保证结构受到外界冲量恒定,在冲击点处设置不可设计域。
3.2 拓扑优化数值方法
由于优化列式(14)允许单元人工密度取0~1的中间值,所以可以使用基于梯度的高效优化方法求解,但是最优结构的密度应该是0~1分布,为此,SIMP方法通常假定单元材料弹性模量和人工密度的关系为
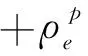
(16)
为了尽量减少在优化结果中出现大量的中间密度单元,通常将惩罚系数p取为3,但是,对于静力柔度优化问题,已经证明p=3时拓扑优化问题非凸,优化迭代可能落入局部最优解。此外,对于动力学问题,p=3也导致局部振型,需要特殊的处理方法。为了避免优化解出现棋盘格式等问题,需要采用线性密度过滤和非线性密度过滤等一系列变量变换,这样的方法称为三场SIMP(three field SIMP)法[21]。
本文采用p=3及上述方法求解了一些例题,但是,由于本文研究的旋转结构动力学问题不同于结构静力分析,优化往往导致局部最优解。本文采用p=1,除了减少了落入局部最优解的可能,还避免了局部振动模式,得到的中间密度在本问题中也可以解释为板的厚度取了中间值。为了解决优化解有灰色单元的情况,引入文献[14]包含灰度信息的加权目标函数为
(17)
式中w为权系数,该值在优化过程中固定,为了统一量级,该值的计算方式取为初始设计的二次型指标除以灰度信息。
4 基于李亚普洛夫方法的拓扑优化列式和方法
为了求解式(14)的优化问题,使用基于敏度的优化方法求解优化问题,需要高效的计算目标函数及其灵敏度的方法。式(15)目标函数是一个在无穷时间区间上的积分,需要时程分析和数值积分,计算目标及其灵敏度十分耗费时间。
4.1 李亚普洛夫方法第二方法
根据李亚普洛夫第二方法,对于渐近稳定的动力学系统,结构在初始时刻受到x(0)的冲击响应后,由于阻尼而使系统的振动逐渐减小,无穷时刻结构位移为0,因此x(∞)取为0。经简单推导可以将式(14a)的目标函数转化为
J=x(0)TPx(0)
(18)
式中P矩阵是对称正定且满足式(19)的代数黎卡提(Ricatti)方程,
ATP+PA=-Q
(19)
式中A矩阵为状态方程(13)的状态矩阵。利用式(18,19)可以把式(15)改写为目标函数容易计算的优化列式,不再需要时程积分。
4.2 振型叠加法
当结构划分为很多单元时,结构矩阵维度高,采用振型叠加法将高维矩阵缩减为低维矩阵,可缩短求解P矩阵的时间。振型叠加法先求解模态方程,
(i=1,2,…)(20)
式中ωi为第i阶频率,φi为第i阶模态。约定模态矩阵Φ=[φ1,φ2,…]相对于质量矩阵M正交归一化,即ΦTMΦ为单位阵。从模态矩阵Φ取出前s阶模态,称为缩减模态,形成矩阵Φs并引入模态坐标φ,使用缩减模态可将板的响应近似为
(21)
将式(20)代入式(13)得到缩减的状态方程为
(22)
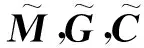
(23)
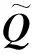
结合李亚普洛夫方法和振型叠加法,旋转板拓扑优化列式(14)可转化为
(24a)
(24b)
(14c~14d)
(24c)
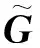
5 算 例
在动力学减振优化中常采用以最大化基频为目标函数减小结构的振动,本文则采用最小化二次型性能指标为目标函数。基频反映的是整个板结构的振动情况,二次型性能指标直接反映的是观察点处的振动情况。下面的第一个算例将比较和讨论不同转速下基于二次型性能指标的优化设计和基于最大化基频的优化设计。
5.1 算例参数、阻尼参数和缩减模态阶数选择
图2给出了旋转板的几何尺寸和工况。板长为 0.4 m,宽为 0.1 m,厚为 0.05 m,密度为 2766.67 kg/m3,弹性模量为6.89×1010Pa,泊松比为 0.3,体分比为 0.5。薄板结构绕A点以转速ω旋转,板的左端固定,右端点B和点C为滑动支座,允许板沿相对体坐标系的水平方向移动,即允许径向移动,但不允许其沿环向移位。在外径处有圆环提供支承的轮盘叶片就可以近似模拟成这样的结构。假定在板稳定旋转后,点D受到沿环向的初始冲击速度v0,v0设置为1 m/s,初始扰动位移设置为0。为了减小撞击点的位移,选取撞击点D为目标函数的减振观察点,如式(15)所示。有限元分析时矩形板划分为120×30,在撞击点处设置长宽各为2个单元、密度为1的不可设计域。
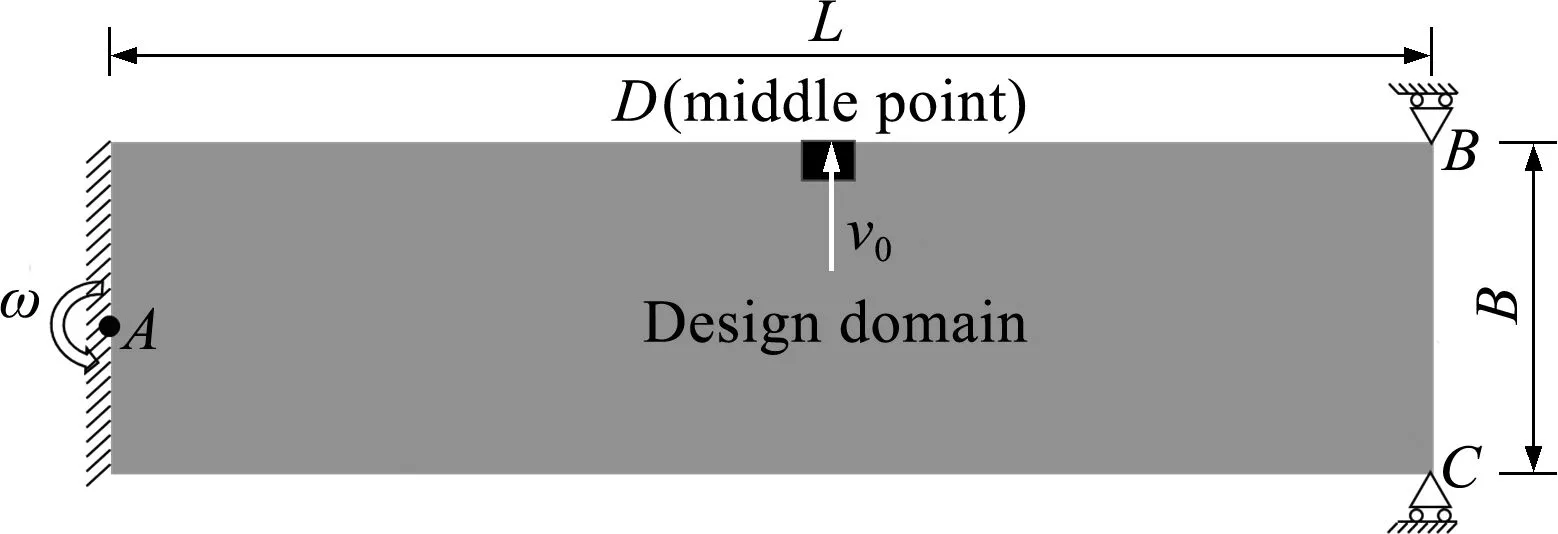
图2 旋转板的几何尺寸和工况
本文采用振型叠加法缩减黎卡提方程,缩减模态阶数选取越多,目标函数越精确,但选择过少的模态数会导致基于模态缩减的多体系统动力学拓扑优化中优化算法不收敛和灰色区域的出现[22]。另一方面,选择的模态过多,缩减的结构矩阵和状态矩阵的规模越大,黎卡提方程求解时间越长。由前面讨论可知,高阶模态的频率如果使得相应的阻尼比ξ大于临界阻尼比1,相应模态的振动不再振荡,并不影响结构的功能。算例中选取的模态阶数使得选取模态的阻尼比都小于1。经过计算,本算例前30阶模态的阻尼比都小于1,故优化时选取30阶缩减模态。
5.2 优化结果
初始设计取满足约束条件的可行设计,采用国际单位制,目标函数在数值计算时乘以1020。表2的第2~4行给出了不同转速下的最优指标值、优化结构的频率及其构型。第5行max Frquency给出了基频最大化的优化结构,这是一个基频为重频率的优化设计。最大化基频问题优化列式可表示为
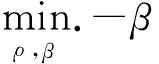
(25a)
β≤ωi(i=1,2,…,nr)
(25b)
(14c~14d)
(25c)
式中nr为计算时控制的特征值数,本文选为3,为了避免模态切换,采用了重特征值的灵敏度分析方法,具体细节参见文献[23]。
由表2可知,随着转速的增加,指标优化得到具有不同基频特性的指标设计。由表2第4列可知,转速0 rad/s和2000 rad/s的优化设计及其指标值或者基频都非常接近。当转速增加到4000 rad/s,优化设计端部的材料加强明显。最大基频设计在转速0 rad/s,2000 rad/s和4000 rad/s下的指标值分别为 1854.85,1442.69 和 1564.16,比指标最小化设计的指标值大约50~60倍,说明对于本问题,基频优化设计并不是在冲击荷载下点D振动最小的设计。图3给出了初始设计和转速为2000 rad/s的指标设计在点D的残余振动的时程曲线,可以看出指标设计比初始设计的点D残余振动衰减要快,说明采用的最小化指标能够减小旋转结构的振动。由表2可知,基频最大设计和指标最小化设计的基频和构型不一样,这说明以二次型性能指标作为目标函数的优化设计没有重频。
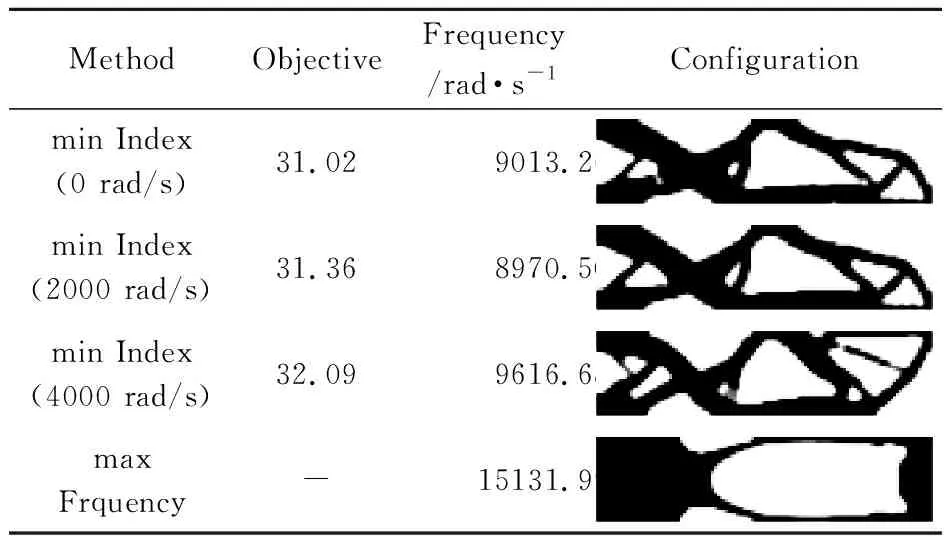
表2 长宽比为4∶1时指标设计和基频设计的比较
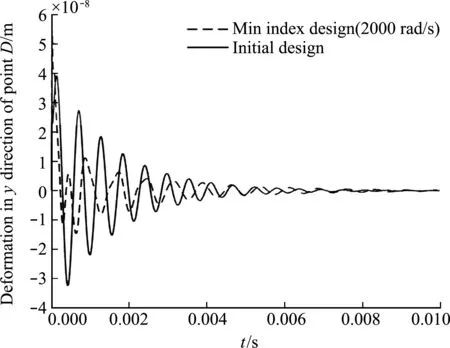
图3 转速为2000 rad/s时初始设计和指标设计点D的Y方向位移响应对比
5.3 边长比、冲击点、观察点及支撑条件对优化结果的影响
为了考虑边长比、冲击点、观察点及支撑条件对优化结果的影响,研究了图4列出的不同问题。图4(a)的边界条件不同于图2结构,该板远端自由,且在该端中点施加集中质量0.5 kg,其左端考虑了只有1/3边界固支和全部固支两种情况。表3 给出了相应于这两种情况的优化设计,可以看出当左端部分固支时,相较于全部固支,指标设计的材料会向固支点移动。图4(b,c)的问题采用 图2 的算例参数,但是冲击点和观察点的位置改变。图4(b)的问题,冲击点和观察点位置不同。图4(c)的问题,观察点和冲击点都在板的中心,表4 给出了相应的优化设计。
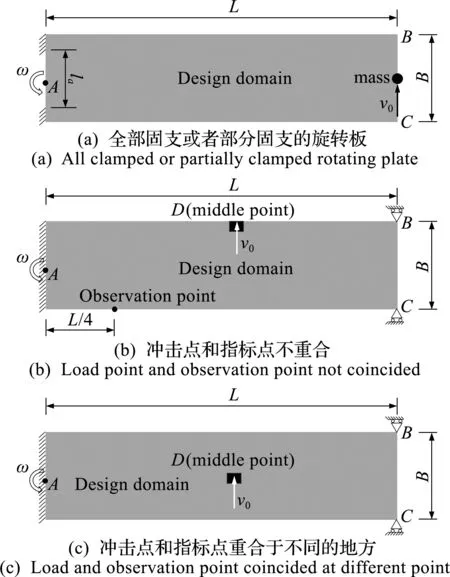
图4 转速为2000 rad/s旋转板不同工况或者边界条件
由表4可知,当冲击点和指标点不重合时,指标设计很难得到清晰的优化结果,这样的问题本质上和柔性机构优化设计相似,后者的荷载作用点和位移控制点不一致,获得黑白结构比较困难;当冲击点与指标点重合移动到其他点时,即图4(c)的情况也很难得到清晰的优化结果,还需要进一步研究其改进方法。此外,本文还计算了长宽比为8∶1的旋转板指标优化,该算例采用表1的荷载参数和材料参数,板的宽度变为0.05 m,长度仍为0.4 m,网格划分为160×20,优化结果列入表5。与长宽比为4∶1不同的是,长宽比为8∶1的指标设计基频和指标不是随转速增加而增加,值得进一步研究。
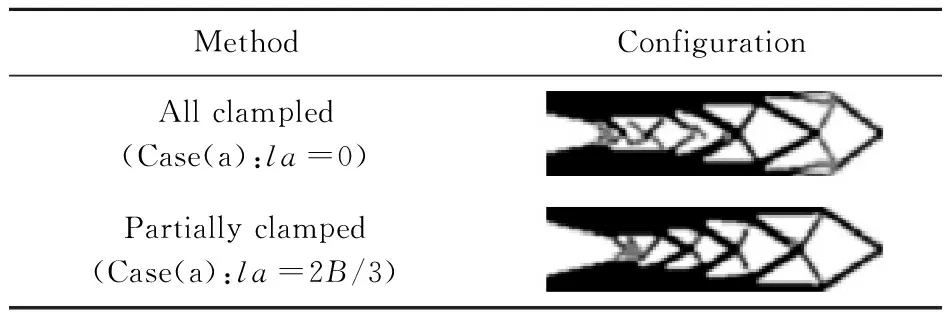
表3 加集中质量的板左端全部固支和部分固支的优化结果比较
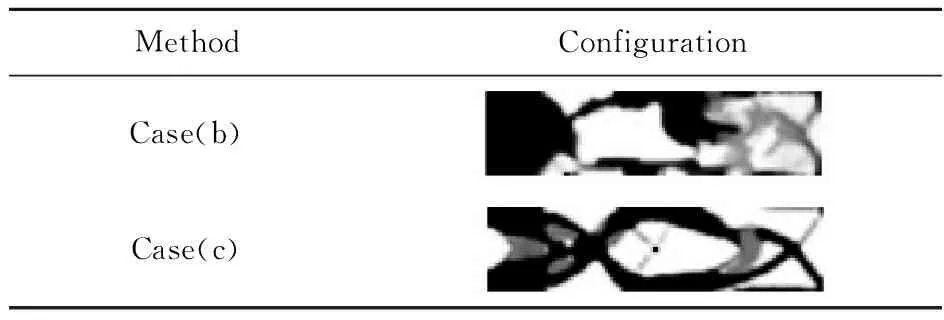
表4 选取指标中不同观察点或者冲击点位置时的优化结果比较
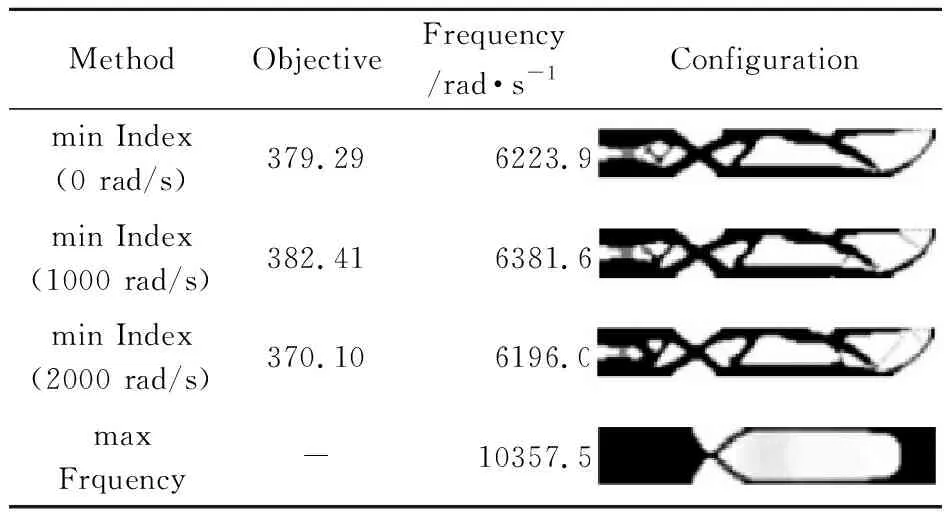
表5 长宽比为8∶1时指标设计和基频设计的比较
6 结 论
本文研究了绕定轴旋转平板结构拓扑优化设计,采用二次型性能指标为目标函数以减小受到冲击荷载时平板结构的振动,得到了比基频最大的拓扑优化设计好很多的设计,且指标最小化设计的拓扑构型与基频最大的设计相差较大。除此,指标设计随着转速的增加,端部材料得到加强且基频增加,间接地反映了旋转带来的惯性效应,还受到边界条件、冲击荷载的位置、观察点的位置和板的长宽比等的影响得到不同的构型,其中冲击点或者指标点改变有可能很难得到清晰的优化构型,需要进一步研究。

