基于MTMD的大跨度人行悬索桥人致振动控制
沈文爱, 曾东鋆, 朱宏平
(1.华中科技大学 土木与水利工程学院,武汉 430074;2.华中科技大学 控制结构湖北省重点实验室,武汉 430074; 3.同济大学 土木工程学院,上海 200092)
1 引 言
桥梁的人致振动问题由来已久,但直到20世纪末伦敦千禧桥[1]和日本T桥[2]等事件发生后才引起学者们的广泛关注。从早期到现在,对于人行桥的振动控制主要有三种方法[3]。
(1) 限制通行人数及防止行人以整齐和规则的步频过桥。
(2) 频率调整法。
(3) 阻尼减振法。
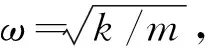
此前,已有学者对人行悬索桥的减振方法进行了研究,如TMD方法[5-10]。但是目前对于大跨度人行悬索桥,特别是主跨大于500 m的人行桥的减振性能研究还较少。本文以一座600 m跨度的人行悬索桥为例,利用有限元软件Midas/Civil建立其有限元模型,结合德国EN03规范,计算了加装MTMD减振系统前后结构的振动响应,并进行了对比分析,评估了其对人致振动的控制性能,为同桥型的减振设计提供重要参考。
2 MTMD设计参数
MTMD全称为多重调谐质量阻尼器(Multiple Tuned Mass Damper),是单个TMD基础上的一种延伸[11],单个TMD具有调频范围窄、控制效果不稳定及不能应对外荷载频率变化的缺陷[12]。而以控制模态频率为中心,将多个TMD按一定的频率宽度分布,可得MTMD系统,得到的控制系统的鲁棒性较强,可以同时控制多阶模态的振动响应,且更易安装,经济实用。MTMD不仅在电塔和高层建筑中有广泛应用,其在控制桥梁人致振动响应时,效果也非常明显,其力学模型如图1所示。

图1 MTMD[13]
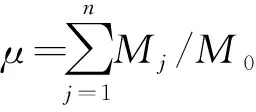
根据相关研究成果,Model 1和Model 4的鲁棒性在五种模型中较优。Model 1中各TMD参数除质量M以外均相同,这样在MTMD系统制作过程中可仅改变各TMD中质量块的质量,为生产制作带来了较大便利,因此,本文采用Model 1进行MTMD系统设计。

表3 MTMD模型列表
3 工程概况
本文考虑的某大跨度人行桥为平面直线无塔悬索桥结构,主缆直接锚固于岩体上,桥面到底谷的距离为234.8m,如图2所示。

图2 某大跨度人行悬索桥
桥梁主缆跨度750m,加劲梁跨度600m,主缆在桥左右两侧各分别对称布置,加劲梁与主缆通过118根悬索相连,加劲梁采用钢箱梁截面,桥梁立面和平面布置如图3和图4所示。
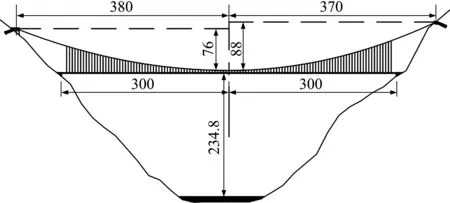
图3 人行悬索桥立面布置

图4 人行悬索桥平面布置
4 结构动力特性分析及人致振动计算
4.1 计算软件及模型
采用Midas/Civil软件建立该人行悬索桥的有限元模型。主缆及悬索采用受拉单元,横梁及边纵梁采用空间梁单元。由于主鞍座直接置于岩体上,刚度较大,故直接采用边界条件来对桥梁两端进行约束。两根主缆的四端均采用6自由度完全约束进行固定,全桥有限元模型如图5所示。

图5 悬索桥模型
4.2 人致荷载模型
本文的人致振动分析采用德国规范EN03推荐的人致荷载模型。EN03规范的荷载模型在TC1~TC5交通级别下的荷载均采用简谐荷载模型,其荷载大小与等效行人密度有关,可表示为
p(t)=Pcos(2πfpt)n′Ψ
(1)
式中P为行人步频为fp时,单个行人荷载的幅值,竖向取280N,纵向取140N,横向取35N;n′为加载面积为S时的等效行人密度,和交通级别有关;S为加载面积,取人能行走的桥面面积;Ψ为折减系数,考虑了行人频率的影响,敏感频率范围以外的折减系数为0。
此外,在加载时,式(1)的荷载函数正负号需与结构振型函数的正负号保持一致。

图6 人致荷载模型折减系数Ψ与频率的关系
4.3 结构动力特性分析
采用Lanczos法计算人行悬索桥动力特性,结果表明该桥基频很低(0.0769Hz)且模态分布密集。因此,本文仅针对德国规范中施加荷载最大(Ψ=1)且具有明显竖向和侧向振动特征的模态进行振动控制设计。表2和表3列出了相关控制模态的信息。可知本文MTMD设计考虑的竖向频率范围为1.715Hz~1.996Hz;横向频率范围为0.714Hz~0.985Hz。需要说明的是,针对敏感频率范围之内(1.25Hz~2.5Hz)的其他振动模态,本文以0.1Hz为激励频率间隔,采用式(1)的人致荷载模型进行减振前后的动力响应分析,以验证MTMD系统在敏感频率范围的人致振动控制性能。
4.4 结构人致振动计算
根据德国EN03规范对桥梁进行人致振动计算。结构模态阻尼比取0.003,振动响应计算采用时程分析法,分析时间取600s(人行速度约为 1m/s,则通过全桥时间约为600s),取桥梁约 1/10跨、1/5跨、3/10跨、2/5跨和1/2跨处节点为观测节点。
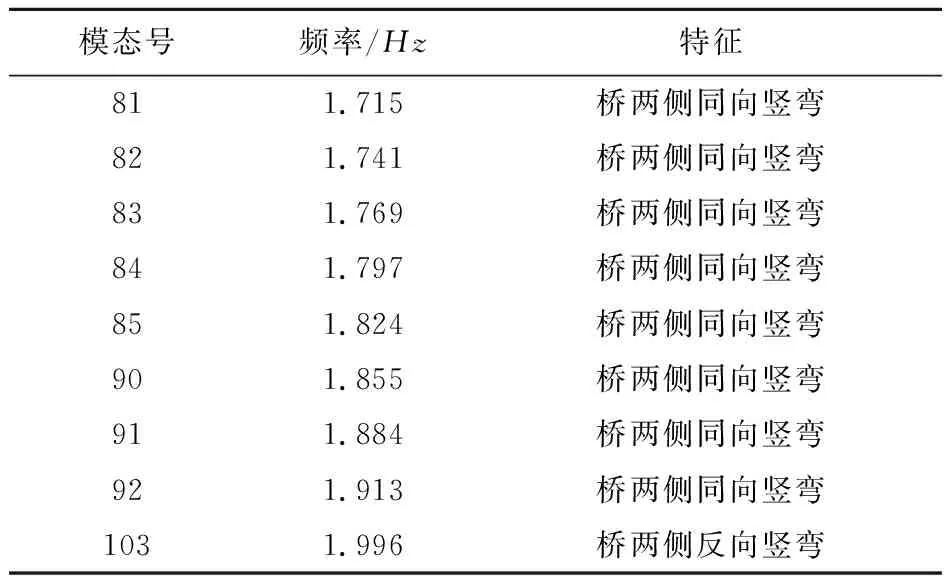
表2 竖向振动控制模态
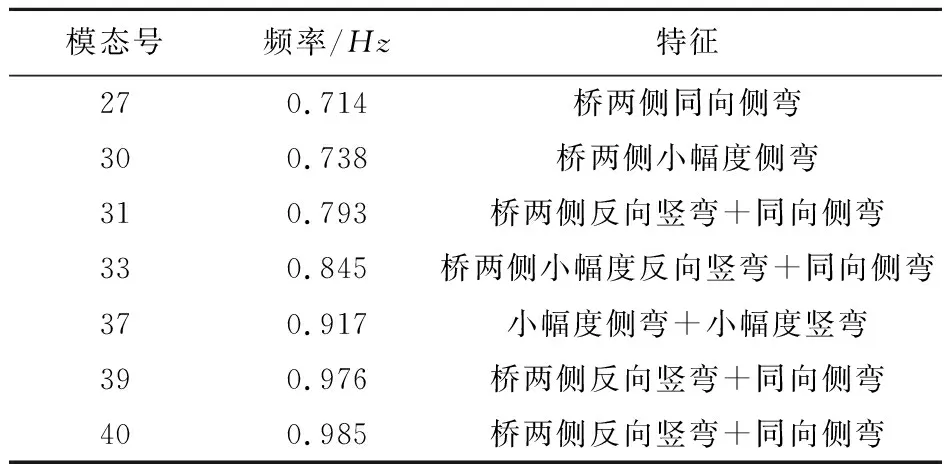
表3 侧向振动控制模态
计算结果表明,在TC4交通级别下,观测点竖向的最大加速度响应超过1/2大于0.5m/s2,其中最大加速度为1.700m/s2。在TC5交通级别下,观测点竖向最大加速度响应几乎全大于0.5m/s2,其中最大加速度为2.080m/s2。此交通级别下,侧向最大加速度响应也达0.200m/s2。因此,若有大量游客在桥上通行,则行走舒适度无法得到保证,甚至可能造成游客及工作人员产生恐慌,需要进行振动控制以减小桥梁的振动响应。
5 人致振动控制设计
5.1 人行桥的竖向振动控制
由于大跨人行悬索桥模态密集,位于敏感频段的竖向模态较多,因此需要同时进行多模态振动控制。本文取第85阶为中心模态,竖向MTMD系统频率以此为中心向两侧延伸,中心频率比取1[13]。
根据桥梁实际情况,全桥布置24个用于竖向振动控制的TMD形成竖向MTMD系统,设计参数列入表4。值得注意的是,除3号TMD外,其余竖向TMD均分别对应表2的竖向振动模态。布置3号TMD的目的是保持整个MTMD系统的中心频率与中心模态频率一致。

表4 竖向MTMD系统控制参数
竖向MTMD的布置位置如图7所示。竖向MTMD系统布置原则如下,1号TMD布置在振型向量最大值处,2号TMD与1号TMD关于桥中心对称布置,1号与2号均往桥中心移动10m得3号与4号点位(对应振型向量较大值处),剩余点位依此类推,每一处布置两个完全相同的TMD,剩余的4个6号TMD在距跨中10m处相对跨中对称布置。

图7 竖向MTMD阻尼器布置
5.2 人行桥的侧向振动控制
侧向振动控制与竖向类似,共布置6个TMD形成MTMD系统,MTMD的布置位置如图8所示,1号、2号和3号均布置在对应模态的振型向量最大值处,设计参数列入表5。
由表5可知,侧向MTMD系统不需要每阶模态均设置对应的子TMD,只需保持MTMD系统的频带(0.714Hz~0.976Hz)足以大致覆盖所有受控的侧向模态即可。

图8 侧向MTMD阻尼器布置

表5 侧向MTMD系统控制参数
6 MTMD振动控制性能分析
布置MTMD系统后,本文按相同方法加载如式(1),再次计算悬索桥在TC5交通级别各阶频率人致荷载下的振动响应及减振率。
6.1 竖向振动响应控制性能
图9对比了加装MTMD减振系统前后,在TC5交通级别条件下,悬索桥1/10跨观测点的81和83阶人致振动响应的加速度时程曲线。可以看出,MTMD系统具有显著的人致振动控制效果。

图9 TC5交通级别不同频率荷载下1/10跨竖向加速度时程
MTMD系统对表2各阶竖向振动模态的减振控制效果如图10所示。可以看出,附加MTMD系统之后,悬索桥在各阶频率荷载作用下的加速度响应大幅减少,减振后的加速度响应最大为0.323m/s2,小于0.5m/s2,达到了最高舒适度级别。此外,考虑人致振动敏感频率范围(1.25Hz~2.5Hz),以0.1Hz为频率间隔进行加载计算,结果表明,观测点减振率普遍大于80%,最大减振率为99.75%。可见,所设计的竖向MTMD系统减振效果非常好,完全抑制了人群荷载导致的加速度响应,使得该人行悬索桥完全满足舒适度的要求。
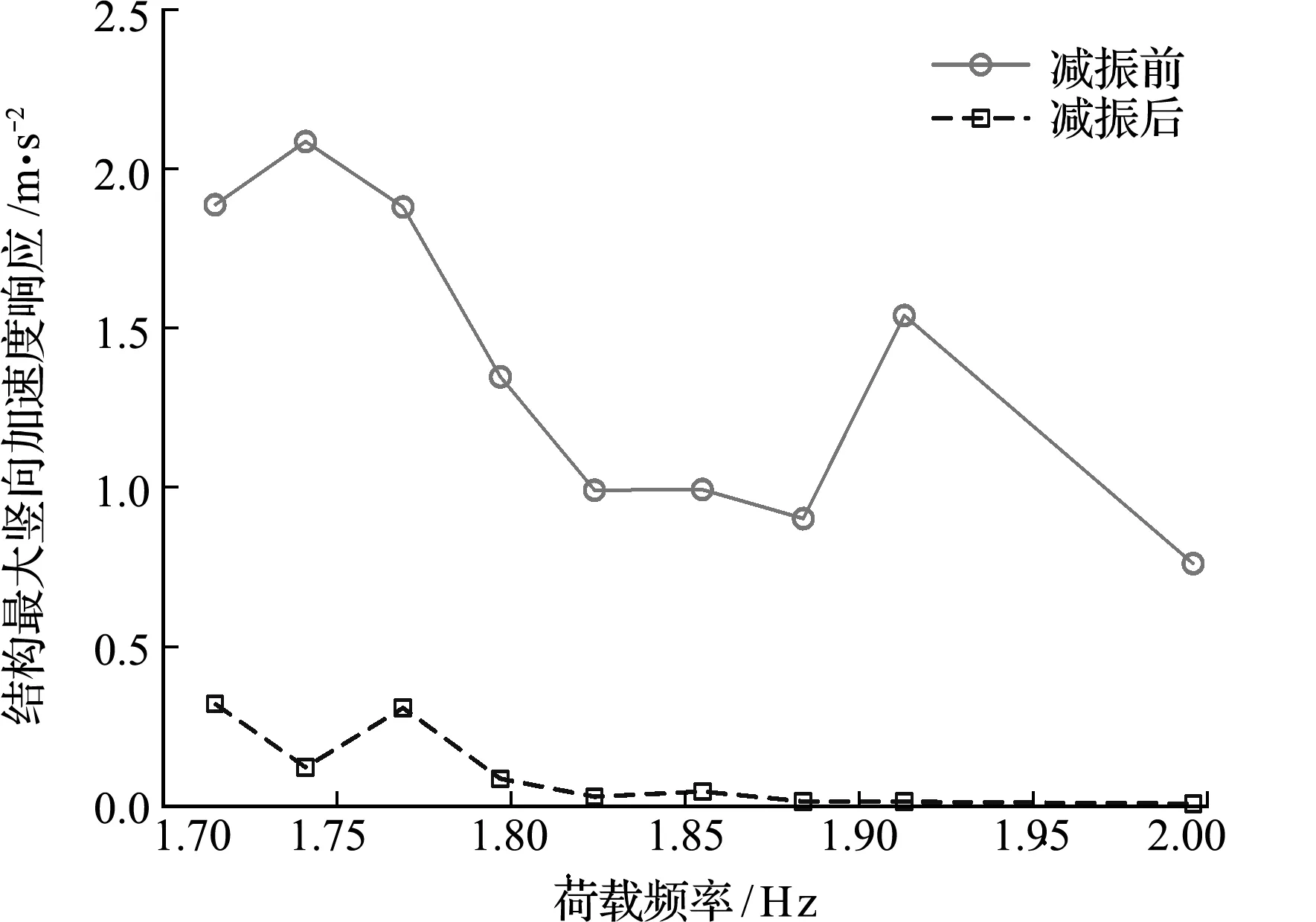
图10 减振前后悬索桥最大竖向加速度响应
6.2 侧向振动响应控制性能
人行悬索桥在TC5交通级别,第27和33阶频率荷载的作用下,1/5跨观测点在加装MTMD系统前后的加速度响应如图11所示。可以看出,侧向MTMD系统同样具有优越的减振性能,可以有效提升大跨度人行悬索桥的振动舒适度。

图11 TC5交通级别不同频率荷载下1/5跨侧向加速度时程
MTMD系统对表3各阶侧向振动模态的减振控制效果如图12所示。可以看出,附加MTMD系统之后,悬索桥在各阶频率荷载作用下的侧向加速度响应受到了有效抑制,减振后的最大响应为0.018m/s2,小于0.1m/s2,观测点减振率普遍大于82%,最大减振率达97.94%,达到了最高舒适度级别。同时,也使人行桥的侧向失稳锁定现象不再可能发生,大大提高了人行桥的安全性。

图12 减振前后悬索桥最大侧向加速度响应
7 结 论
大跨度人行悬索桥具有自振频率低、阻尼比小和柔度大的特点,其在行人荷载的敏感频段具有非常密集的振动模态,因此人致振动控制问题是其设计和安全服役的关键。MTMD系统具有控制频带较宽、可覆盖多阶振动模态及鲁棒性强的优点,是大跨度人行悬索桥人致振动控制的优先选项。本文采用两个MTMD系统分别对悬索人行桥竖向及侧向人致振动同时进行多模态控制。研究发现,即便悬索桥跨度达到了600m,经合理设计的MTMD系统减振效果仍十分显著。在拥挤行人工况下,人行悬索桥的竖向和侧向人致振动响应均抑制在最高舒适等级范围内,同时消除了大跨度人行悬索桥发生侧向锁定失稳的可能性。其次,本文研究发现,在振型向量值较大处布置MTMD系统,且符合对称布置原则,可取得较优的减振效果。本文研究结果为同类型大跨度人行悬索桥的人致振动控制提供了一个重要的参考依据。进一步的研究应重点关注MTMD系统人致振动多模态控制的最优设计问题。

