应变率相关的橡胶本构模型研究

魏家威，石霄鹏，冯振宇

（1. 中国民航大学安全科学与工程学院, 天津 300300；2. 民航航空器适航审定技术重点实验室, 天津 300300）

橡胶作为一种有机高分子材料，在大变形下能迅速有力地恢复变形，在生产和生活中得到广泛应用。橡胶的力学行为非常复杂，其本构关系是非线性的，简单依赖单轴拉伸（simple tension，ST）实验并不能准确描述材料包括压缩和剪切在内的所有力学行为。在橡胶材料的基础力学性能实验中，单轴拉伸实验与等双轴压缩实验等效，平面拉伸（planar tension，PT）实验与纯剪切实验等效，等双轴拉伸（equibiaxial tension，ET）实验与单轴压缩实验等效[1]。研究发现，同时采取单轴拉伸、平面拉伸和等双轴拉伸3 种实验方法获得的数据能更准确地描述橡胶的力学行为[1–3]。

建立超弹性本构模型对于橡胶材料研究具有重要的意义。橡胶类材料的超弹性本构模型可分为两类：唯象模型和分子统计理论模型。常见的唯象模型有Mooney-Rivlin（M-R）模型[4–5]、Yeoh 模型[6]、Ogden 模型[7–8]等；常见的分子统计理论模型有Arruda-Boyce（A-B）模型[9]等。

针对Treloar[10]关于硫化橡胶的单轴拉伸、平面拉伸和等双轴拉伸实验下的经典准静态实验数据，Boyce 等[11]、Steinmann 等[12]、Marckmann 等[13]对比了多种经典超弹性本构模型的拟合能力，研究表明，只有很少部分本构模型能够较好地拟合不同加载条件下（单轴拉伸、平面拉伸和等双轴拉伸）橡胶的实验数据。近年来，许多新的本构模型[14–18]被用于描述橡胶材料的完整超弹性行为，然而，这些新模型的拟合能力尚缺乏对比研究。

橡胶类材料还具有比较明显的应变率相关性[19–21]。鉴于橡胶力学行为的复杂性，通常将与应变率无关的非线性弹性行为和与应变率相关的弹性行为解耦并分别描述，即分别采用超弹性本构模型和黏弹性本构模型表征其与应变率无关的非线性弹性行为和与应变率相关的弹性行为。周相荣等[22]提出了一种基于Yeoh 函数的黏超弹性本构模型，用来描述橡胶材料在中高应变率下的响应。林玉亮等[23]建立了考虑应变率效应的Ogden 模型，描述了硅橡胶在高应变率压缩下的力学行为。杨建兴等[24]基于三参数的M-R 模型，构建了高应变率相关的硅橡胶黏超弹性本构模型。然而，由于橡胶类材料的动态实验数据较少，且实验数据通常仅限于一种加载状态，因此，目前还没有一种通用的应变率相关的本构模型。

本研究基于Treloar[10]关于硫化橡胶的单轴拉伸、平面拉伸和等双轴拉伸实验下的经典准静态实验数据，对比分析M-R 模型、修正的M-R 模型、Yeoh 模型、修正的Yeoh 模型、Ogden 模型和A-B 模型的拟合能力，选取其中一种形式简单且拟合能力较好的模型，以此为基础建立应变率相关的黏超弹性本构模型，以期为橡胶材料的本构模型选择提供参考。

1 准静态下橡胶超弹性本构模型

1.1 M-R 模型

Mooney[4]和Rivlin 等[5]建立了M-R 类数学模型，其应变能密度函数形式为

应变能密度函数中的模型参数确定了超弹性模型的力学响应。为了在超弹性分析中获得正确的结果，需要评估被测材料的模型参数。这些参数通常是根据实验的应力-应变数据通过曲线拟合得出的。来自多种变形状态下的数据组合比单一变形下的数据更好，可以得到更准确的超弹材料参数。因此，本研究采用3 种实验方法（单轴拉伸、平面拉伸和等双轴拉伸）获得的组合数据，对橡胶材料的本构模型参数进行拟合。

将式(2)中的应变能公式代入式(3)中，可得M-R 模型在3 种基本变形模式下载荷作用方向上的工程应力与伸长比关系

1.2 Yeoh 模型

若忽略式(1)中(I2–3)项的影响，且取i=3，则可以得到Yeoh 模型。Yeoh 模型的应变能密度函数形式为

1.3 Ogden 模型

Ogden 模型的应变能密度函数形式为

1.4 A-B 模型

A-B 模型的应变能密度函数形式为

2 准静态下本构模型参数确定及验证

2.1 本构模型参数拟合

为了得到橡胶材料超弹性本构模型的精确参数，利用MATLAB 软件，同时对单轴拉伸、平面拉伸和等双轴拉伸3 种实验数据进行拟合。采用最小二乘法拟合实测应力-应变数据点与本构模型计算得到的应力-应变关系。具体方法为：寻找一组合适的模型参数，使计算应力与实测应力的绝对值误差S最小。绝对误差S的表达式为

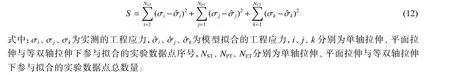
2.2 模型拟合优度

采用拟合优度系数R2评价各模型的拟合优度，R2可通过计算总偏差平方和Stot以及残差平方和Serr得到

3 数据处理及分析

3.1 M-R 模型及修正的M-R 模型

首先使用M-R 模型对Treloar[10]的实验数据进行拟合，拟合结果如图1 所示。图1 显示，M-R 模型在同时拟合3 种变形实验数据时，只在小变形范围内的拟合效果较好；在大变形处，拟合效果较差。另外，随着伸长比的增加，M-R 模型的拟合结果呈近似线性变化趋势，没能很好地反映单轴拉伸、平面拉伸和等双轴拉伸的实验数据走向。

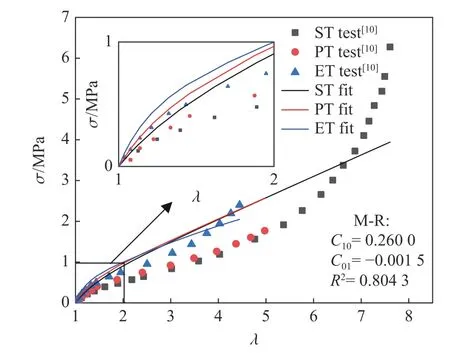
图1 基于M-R 模型拟合的工程应力-伸长比的结果Fig. 1 Fitting results of the principle stress versus the principle stretch using M-R model

上述问题可以通过增加高阶项来解决。Tschoegl[25]对式(1)保留不同的高阶项，得到了如下6 种修正的M-R 超弹性本构模型

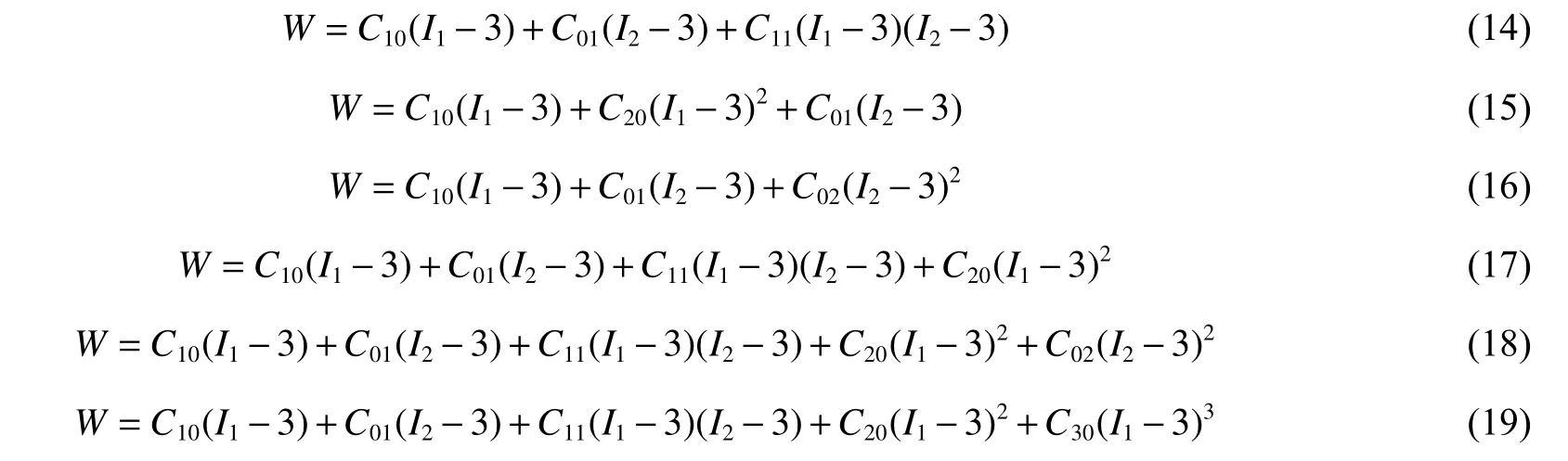
理论上，应变能函数所取的项数越多，模型越可能准确地描述材料的真实力学行为，但是此时需要确定的参数也越多，模型也越复杂，不便于工程应用。因此，选用含3 个参数的修正M-R 模型形式（即式(14)、式(15)、式(16)）进行数据拟合。式(14)、式(15)、式(16)拟合的优度系数R2分别为0.8227、0.9704、0.8064。根据R2的数值大小并兼顾模型的简洁性，最终选用式(15)作为应变能密度函数。以下所提到的修正后的M-R（modified M-R）模型均为该模型。

修正后的M-R 模型在3 种基本变形模式下载荷作用方向上的工程应力与伸长比关系为

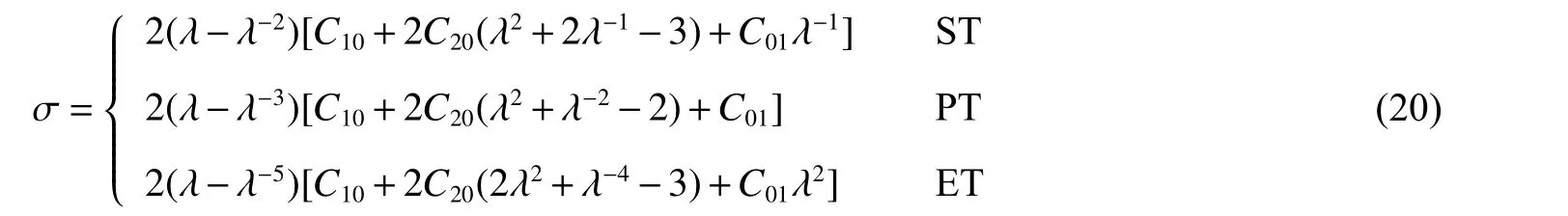
M-R 模型和修正后的M-R 模型的拟合结果对比如图2 所示，修正的M-R 模型的拟合参数标于图中。由于添加了高阶项，修正后的M-R 模型在大变形处也能较好地反映材料的真实响应，大幅提高了实验数据的拟合精度。

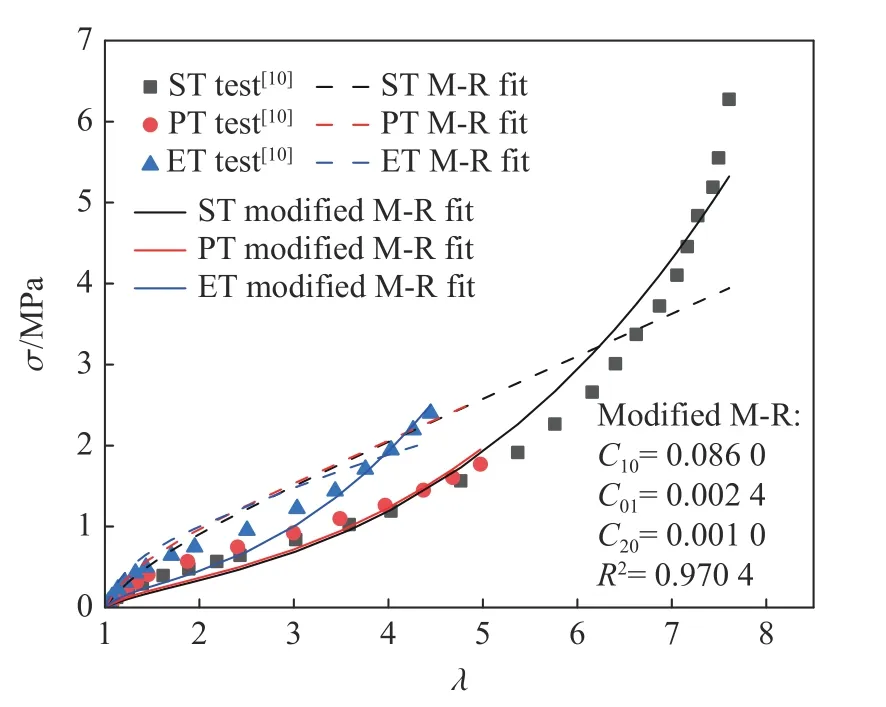
图2 M-R 模型和修正后的M-R 模型拟合结果对比Fig. 2 Comparison of fitting results between M-R model and the modified M-R model

3.2 Yeoh 模型及修正的Yeoh 模型

使用Yeoh 模型对Treloar[10]橡胶实验数据进行拟合，结果如图3 所示。图3 显示，Yeoh 模型对3 种实验数据进行拟合时，单轴拉伸和平面拉伸实验数据的拟合效果较好，等双轴拉伸实验数据的拟合存在一定偏差。此外，由于忽略I2的影响，随着伸长比的增加，基于Yeoh 模型的数据拟合呈现“偏软”的缺点。

图3 基于Yeoh 模型拟合的工程应力-伸长比的结果Fig. 3 Fitting results of the principle stress versus the principle stretch using Yeoh model

Yeoh 模型和修正的Yeoh 模型对Treloar[10]橡胶实验数据的拟合结果如图4 所示，修正的Yeoh 模型的拟合参数也标于图中。可见，修正后的Yeoh 模型很好地克服了原模型随着伸长比增加而“偏软”的缺点，等双轴拉伸数据的拟合效果有明显改善，单轴拉伸和平面拉伸数据的拟合精度进一步提高。

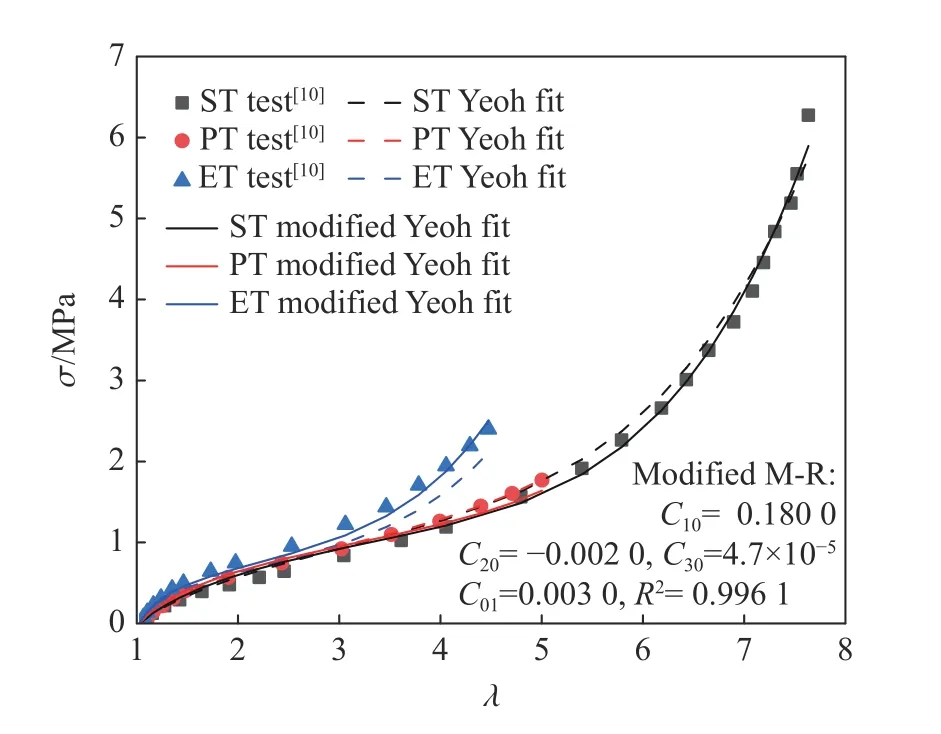
图4 Yeoh 模型和修正后的Yeoh 模型拟合结果对比Fig. 4 Comparison of fitting results between Yeoh model and the modified Yeoh model

3.3 不同模型对比

图5 给出了Ogden 模型（N=2, 3）和A-B 模型对Treloar 实验数据的拟合情况，拟合参数均标于图中。

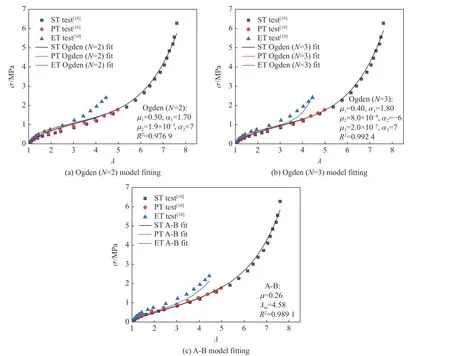
图5 不同模型拟合Treloar3 种实验数据的结果Fig. 5 Fitting results of different models of Treloar’s three kinds of experimental data

M-R 模型、修正的M-R 模型、Yoeh 模型、修正的Yoeh 模型、Ogden 模型（N=2，3）以及A-B 模型的拟合优度系数R2列于表1 中。从表1 可以看出，所有模型的拟合优度系数均在0.97 以上，说明各模型的拟合效果良好。

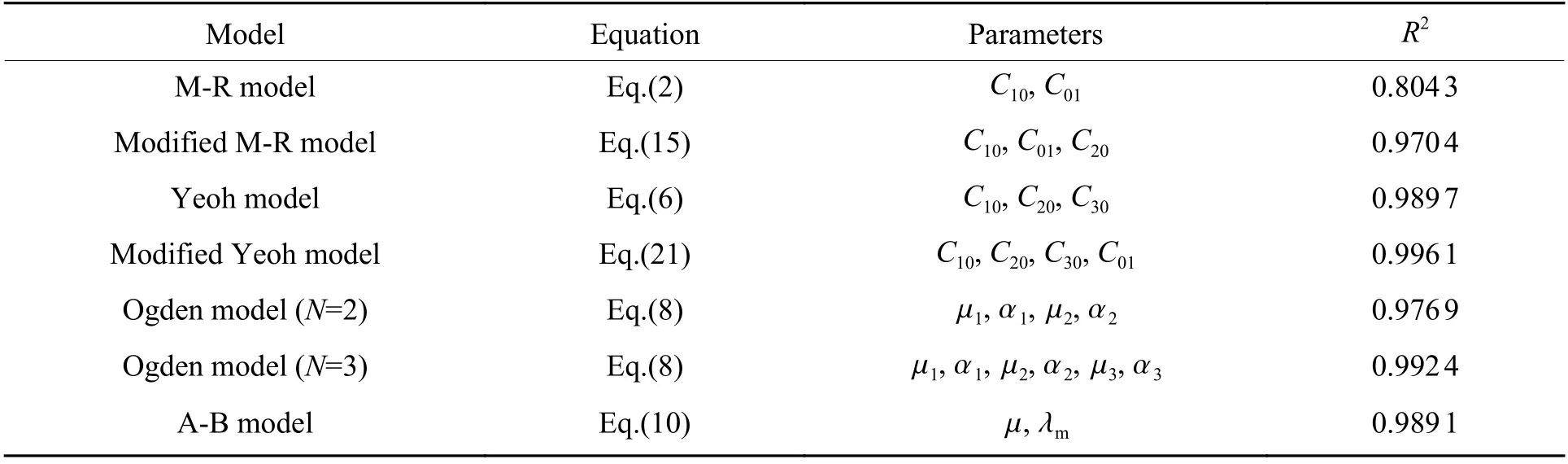
表1 不同超弹性模型对 ST、PT 和 ET 实验数据的拟合效果比较Table 1 Comparison of fitting results of different hyperelastic models on ST, PT and ET experimental data

为进一步研究修正后的M-R 模型和修正后的Yoeh 模型的拟合能力，将它们与Ogden 模型和A-B模型的拟合结果按照实验类型进行对比，结果如图6 所示。对于单轴拉伸数据，5 种模型的拟合效果均良好，拟合结果与实验数据之间的误差较小；对于平面拉伸数据，修正的Yeoh 模型和Ogden 模型（N=3）的表现优异，基本上与实验数据重合，而其余3 种模型的拟合结果出现了一定偏差；对于等双轴拉伸数据，除Ogden 模型（N=2）以外，其余模型均可以反映实验数据的真实变化趋势。通过与Ogden 模型、A-B模型的对比，验证了修正的M-R 模型、修正的Yeoh 模型的拟合能力较为理想。

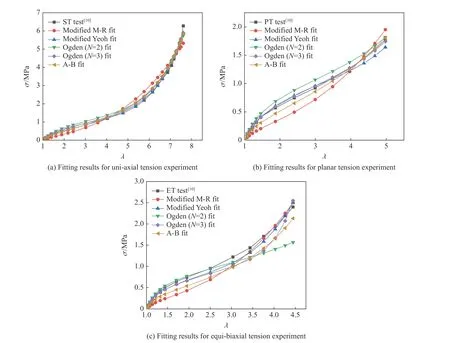
图6 不同实验类型下不同模型的拟合结果对比Fig. 6 Comparison of the fitting results of different models for different experiment types

4 考虑应变率的情况

4.1 M-R 黏超弹性本构模型

式中： θ0、 β为模型参数，由实验确定； ε˙0为特征应变率，为方便计算，取为0.001 s−1。

最终得到一个唯象黏超弹性模型，其一维流变学形式如图7 所示，即超弹性的弹簧（对应于图中的下部分）和Maxwell体（对应于图中的上部分）并联，超弹性弹簧与Maxwell体分别对应橡胶的非线性弹性响应和黏弹性响应，其中超弹性模型使用修正的M-R 模型。本研究采用修正的M-R 模型（式(15)）描述的黏超弹性本构关系进行参数分析。

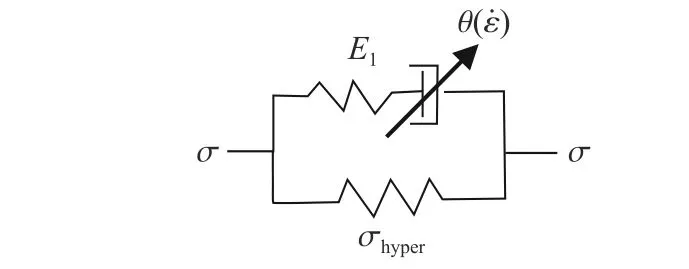
图7 黏超弹性模型示意图Fig. 7 Schematic diagram of visco-hyperelastic model

4.2 数据处理及分析

图8 是采用4.1 节建立的M-R 黏超弹性本构模型拟合硅橡胶的单轴拉伸实验数据[29]的结果。图8显示，拟合结果与实验数据符合较好，对于1400 s−1高应变率下的单轴拉伸实验数据，建立的M-R 黏超弹性本构模型也能较好地反映出实验数据的变化趋势。说明本研究提出的基于应变率相关的Maxwell体和超弹性弹簧（采用修正M-R 模型描述其本构关系）并联得到的唯象黏超弹性模型能很好地描述硅橡胶材料在大应变率跨度内单轴拉伸时的力学变形特征。

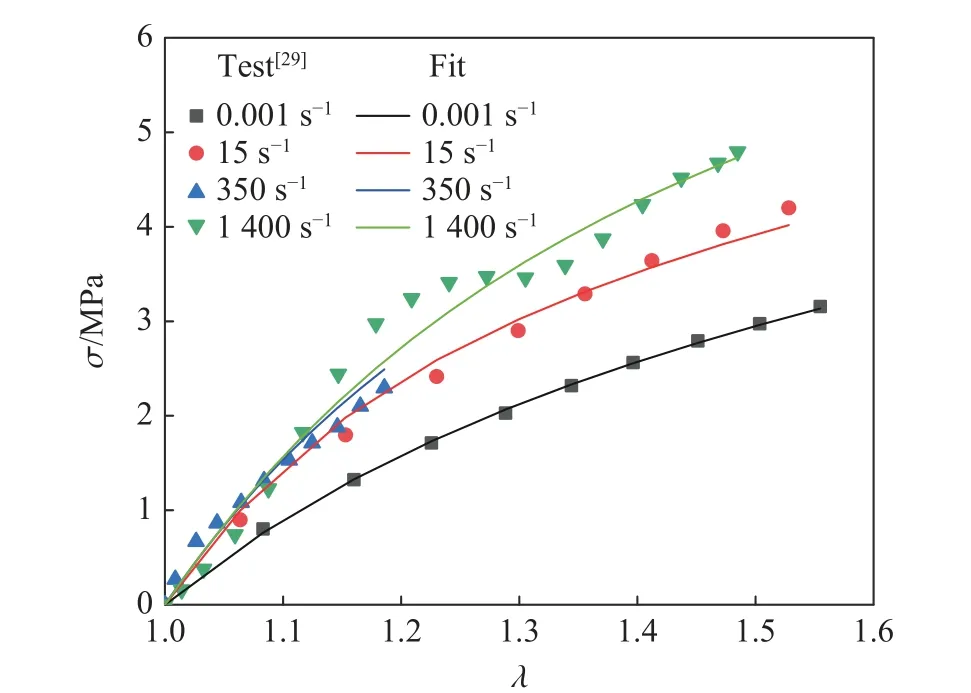
图8 M-R 黏超弹性本构模型拟合硅橡胶单轴拉伸实验数据[29]的结果Fig. 8 Fitting results of M-R visco-hyperelastic constitutive model for the uni-axial tensile experimental data of silicone rubber[29]

图9 是采用4.1 节建立的M-R 黏超弹性本构模型拟合硫化橡胶的单轴压缩实验数据[28]的结果。图9 显示，对于硫化橡胶的动态压缩数据（包括准静态压缩和高应变率压缩实验数据），本研究建立的黏超弹性模型大体上都能很好地进行拟合。在590 s−1中应变率情况下，模型的拟合效果较差，不能很好地反映中应变率压缩下实验数据的变化趋势。

图9 M-R 黏超弹性本构模型拟合硫化橡胶单轴压缩实验数据[28]的结果Fig. 9 Fitting results of M-R visco-hyperelastic constitutive model for the uni-axial compression experimental data of vulcanized rubber[28]

表2 给出了黏超弹性本构模型对单轴拉伸和单轴压缩试验数据的拟合参数和拟合优度系数R2。可见，黏超弹性本构模型对两种实验数据的拟合优度系数均在0.95 以上，说明该模型的拟合效果良好。

表2 单轴拉伸和单轴压缩实验的拟合参数值Table 2 Fitting parameter values of the uni-axial tensile and the uni-axial compression experiment

综上所述，本研究建立的黏超弹性本构模型可以很好地拟合中低应变率下的单轴拉伸数据，对于高应变率下的单轴拉伸数据拟合效果略差，但仍可反映高应变率下的变化趋势；另外，该模型可以很好地拟合低应变率和高应变率下的单轴压缩数据，但对于中应变率下单轴压缩数据的拟合效果不理想。

5 结论及展望

(1) M-R 模型对于橡胶的小变形行为拟合较好，但是无法很好地预测单轴拉伸、平面拉伸和等双轴拉伸的实验数据走向。Yeoh 模型对于橡胶的大变形行为拟合较好，但是由于忽略I2的影响，导致随伸长比的增加Yeoh 模型呈现“偏软”的缺点。修正后的M-R 模型和修正后的Yeoh 模型明显改进了原模型的缺点，拟合精度进一步提高。

(2) 修正后的M-R 模型、修正后的Yeoh 模型、Ogden 模型和A-B 模型对Treloar 的3 种实验数据的拟合优度均在0.97 以上。与Ogden 模型和A-B 模型的对比结果显示，修正后的M-R 模型和修正后的Yeoh 模型的拟合能力较为理想。

(3) 考虑到橡胶材料力学行为的应变率相关性，需建立橡胶的黏超弹性本构模型。基于修正的M-R模型和Maxwell 模型建立的黏超弹性橡胶本构模型对单轴拉伸和单轴压缩实验数据的拟合优度均在0.95 以上，表明该黏超弹性橡胶本构模型能较好地表征橡胶在大应变率范围内单轴拉伸和单轴压缩情形下力学行为的非线性和应变率相关特性。