旋风分离器支撑曲梁设计

万丛伟 高 玲 陈健陵

（东方电气集团东方锅炉股份有限公司，四川 自贡 643001）

1 理论计算

将曲梁简化为两跨连续曲线梁，两端铰支，中间为竖向链杆支座。曲率半径为4297.5mm，集中力274.4KN。由于钢梁跨度不大，自重比较小，计算时不考虑自重均布荷载，在验算时相应的扩大弯矩剪力。

2 曲梁计算

计算简图如图1 所示，梁上共七个集中力，各集中力作用点和O 点连线与OA 夹角分别为13°、21°、28°、36°、43°、51°、58°。

图1 曲梁计算简图

2.1 曲梁截面尺寸确定

钢结构设计标准GB50017-2017 中6.2.4 节[1]，当钢箱梁满足：

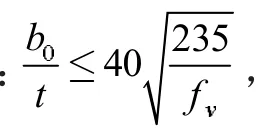
选取曲梁1#尺寸为：宽350mm，高320mm，壁厚28mm。

2.2 支座B 处负弯矩计算

由我国学者姚玲森所出版的《曲线梁》一书[3]，在AB、BC 两跨上各作用一个集中力时，支座B 处负弯矩为：

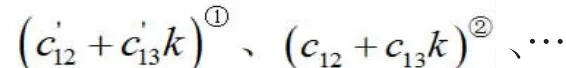
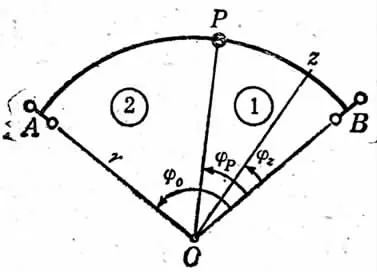
图2 单跨计算简图

对于梁1#，两跨的荷载、曲率和曲率中心角均相等，即 γ=1，并且当第1 跨内有荷载p 作用时，上式（1）可写成：

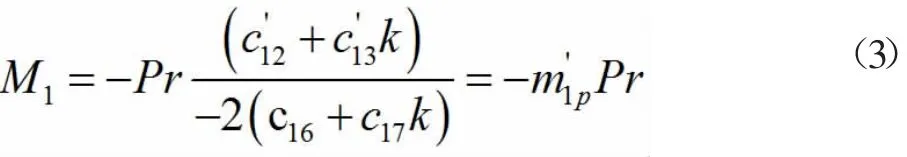
同理，荷载P 作用在第2 跨内时：

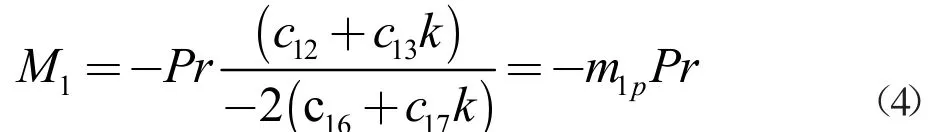
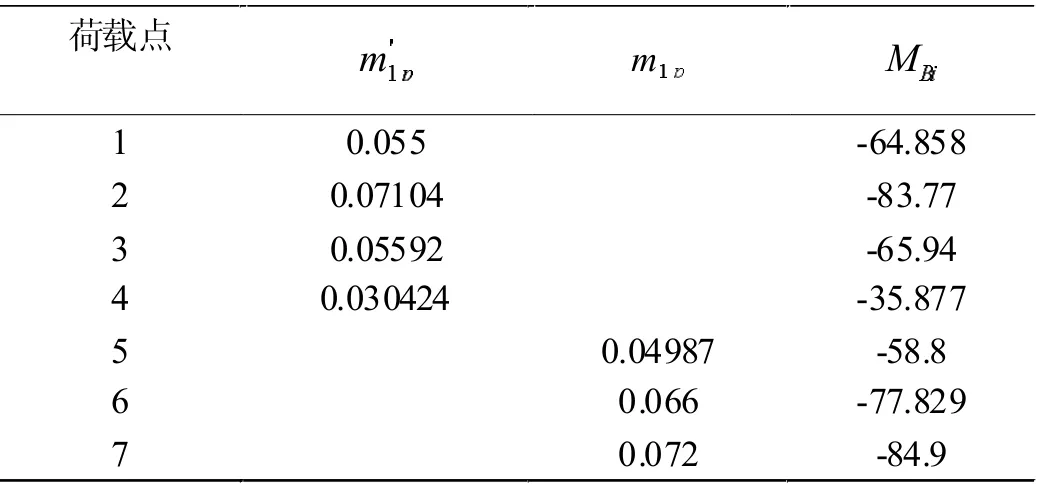
表1 各集中力作用下B 支座弯矩

可得B 点弯矩:

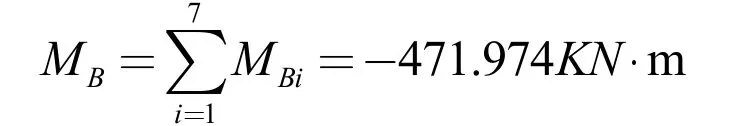
2.3 B 支座处剪力

《曲线梁》书中给出了各截面的剪力影响线。

当荷载P=1 作用于第一跨时：

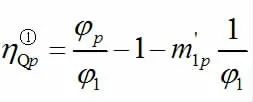
当荷载P=1 作用于第二跨时对于第一跨任意截面的剪力影响线为：

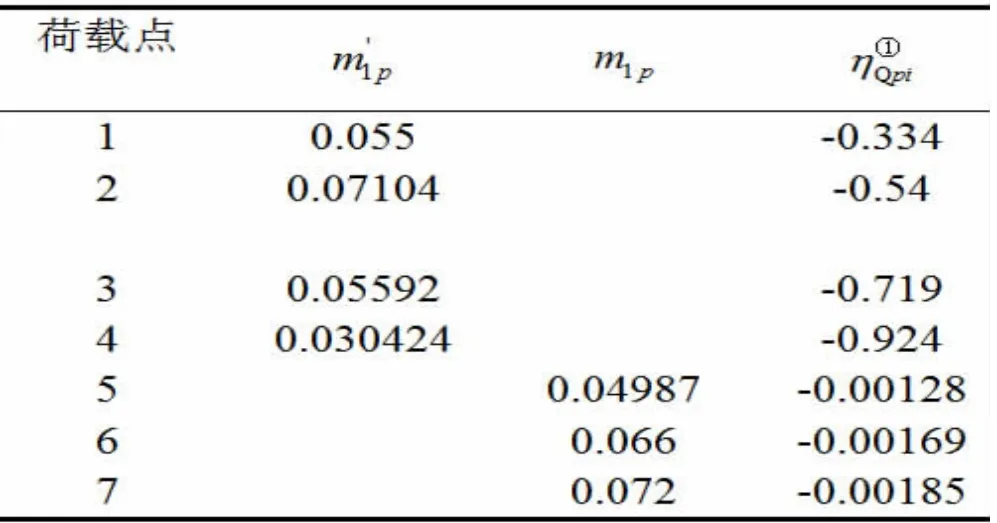
表2 各集中力作用下B 支座剪力

当在有较大弯矩和剪应力同时作用时，构件应满足：

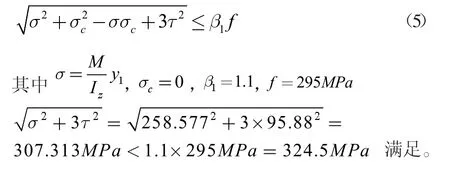
2.4 AB 跨中处弯矩

《曲线梁》中给出曲线梁上任意截面 φ的弯矩影响线：

2.4.1 当单位荷载作用在第一跨内，且荷载位于计算截面左边 （≥ φ ≥φ）时：

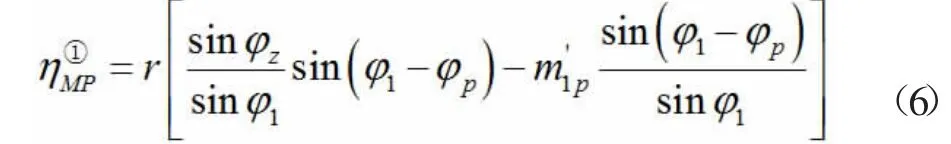
当荷载位于计算截面右边 （φ ≥ φ≥0）时

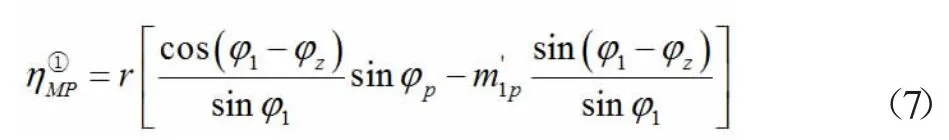
2.4.2 当单位荷载作用在第二跨时：

对于第一跨内任意截面 φz的弯矩影响线：

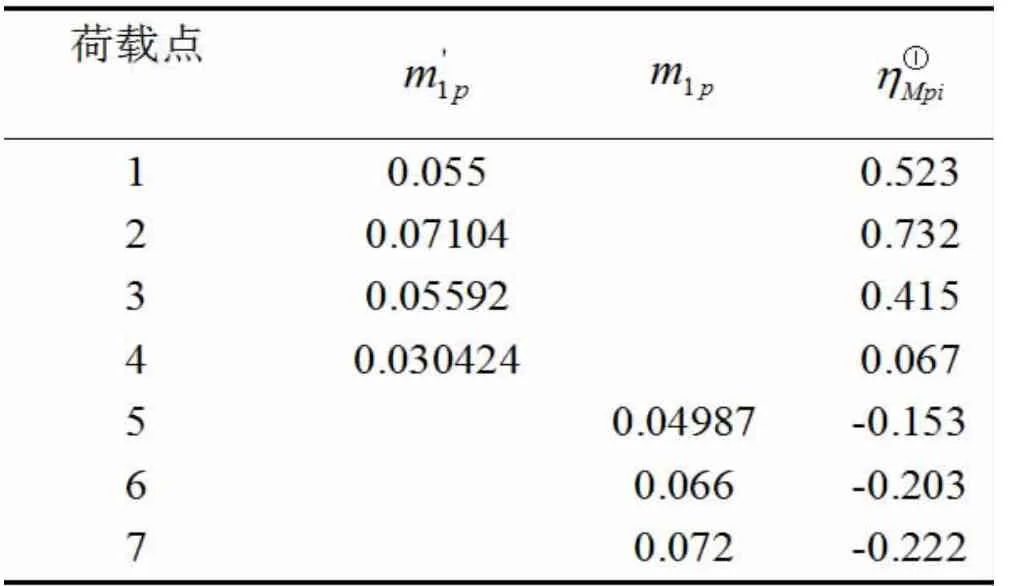
表3 AB 跨中弯矩计算

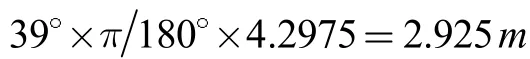
3 有限元模拟

利用扫掠创建三维实体曲梁部件，长度单位为毫米，随后创建加筋板、耳板、侧向支撑以及支撑梁，这里将下面支撑曲梁只取支撑部位周围的一段长度，并将支撑梁截断处的截面固结进行简化模拟。材料为Q355B，弹性模量密度为7850kg/m3，泊松比为0.3。各部件之间通过绑定相互作用在一起，每个加载点对应位置，在梁内设置12mm 厚加筋板，加筋板上侧与上翼板接触处不绑定。在耳板孔洞处各设置一个参考点，参考点与孔洞耦合后施加集中力 274400× 1 .35 =370440N。设置网格形状为四面体，划分网格，见图3。

图3 曲梁网格划分

3.1 曲梁模拟结果

由于在前面理论计算中没有考虑加筋板、侧向支撑等的作用，以及实际工程中支座形式与理论计算中简化的支座有些差异，因此在有限元模拟结果中，应力最大值以及应力最大位置也发生了一定的改变（见图4，图5）。由模拟结果可知，应力最大值为237.5MPa，最大应力位置大致在跨中支座处；最大挠度为1.382mm＜L/500=5.85mm，满足。应力随时间变化曲线如图6 和图7所示。

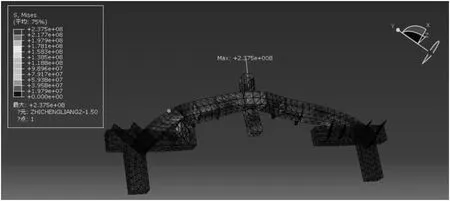
图4 曲梁正应力模拟结果

图5 曲梁剪应力模拟结果

图6 正应力变化曲线

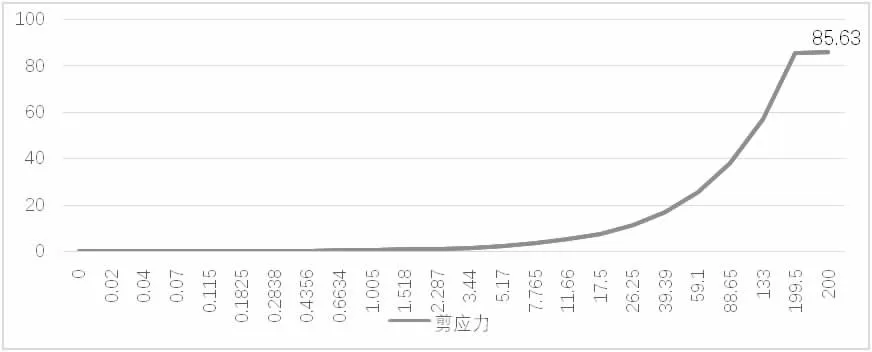
图7 剪应力变化曲线

3.2 弹性屈曲分析结果

进行弹性屈曲分析曲梁的临界荷载，将分析步设置为线性摄动中的屈曲，把各集中力大小改为单位1，模拟结果如图8 所示。临界荷载为特征值EigenValue 与单位荷载的乘积，从结果可看出特征值很大，则说明曲梁不会发生弹性失稳。

图8 曲梁屈曲分析结果

4 与《建筑结构静力计算实用手册》计算结果比较

由《建筑结构静力计算实用手册》P59 第3 项“对称集中荷载作用下任意截面的弯矩及扭矩”[4], 可得曲线梁在对称及反对称集中荷载作用下任意截面的弯矩以及扭矩。

由于计手册里的公式只适用于单跨曲线梁，这里将两跨连续梁1#、2#、3#拆成两个单跨梁大致计算AB 跨中处弯矩，并与利用《曲线梁》中公式计算得到的AB 跨中弯矩进行比较，比较结果也可以看出两种方法计算得到的数值相差较多，如表4 所示。其中《曲线梁》所对应的弯矩可通过式（6）、（7）、（8）求得，式中所需参数在前面计算中也都已求出，代入即可。

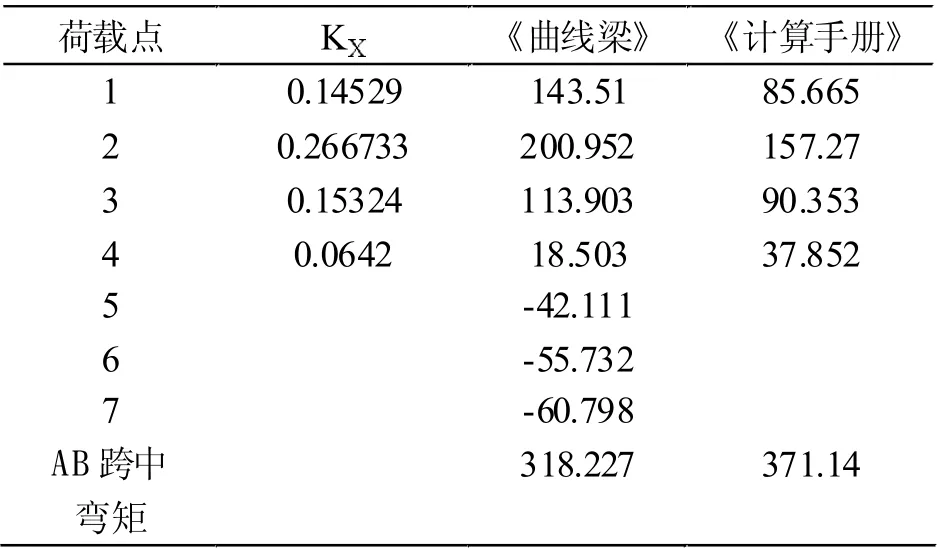
表4 两种方法计算AB 跨跨中弯矩