基于有限元的元动作装配单元薄弱点分析

葛红玉，刘宝强，王 拓，刘 园，张传伟，杨满芝

(西安科技大学机械工程学院，陕西 西安 710054)

随着我国制造业的发展，机械产品呈现出复杂化与多样化的发展趋势[1]。机械产品的性能是由设计、制造、装配等过程共同决定的。复杂机械产品的结构如何分解到元动作级别需要一套分解流程来保证，因此需要研究分解流程和分解模型,研究整机到元动作的映射及整机功能与基本功能之间的关系。元动作装配单元是保证产品功能的基本单元。

当前在机械产品研究领域，杨勇等[2]通过机床动静态特性分析确定薄弱结构部件，提出了基于结构-整机性能映射模型的机床薄弱件结构优化方法。宋守许等[3]提出了产品设计参数与服役特性映射模型的建模流程。宋义顺等[4]建立了具有加工误差的滚珠丝杠副参数化模型，对研究滚珠丝杠副的传动精度具有非常重要的意义。金熙哲等[5]基于功能—行为—结构映射的机构系统概念设计模型，提出了构造功能与有效工作时段动作映射矩阵的方法。张根保等[6]对主运动之间关系进行了耦合解耦分析，完成了关键质量特性在功能—运动层的传递。马晓茜等[7]将多层级分析法运用到复杂机电产品的整机、部件、零件层模块化设计中，为它们高效模块化解决方案的实现提供了参考。杨得玉等[8]提出了基于功构映射的拆卸设备设计方法，定义了拆卸设备设计过程的需求功能映射模型和功能结构映射模型。徐荣华[9]提出基于功能本体的消化吸收再创新设计策略，实现了从已有产品结构到其功能的映射。

上述文献主要针对整机性能、参数设计、主运动耦合关系进行研究，为整机性能保障提供了理论基础。由于元动作性能直接决定整机的性能，因此进一步研究整机到元动作映射关系显得尤为重要。

基本单元性能方面，张根保等[10]建立了影响因素自相关矩阵、各个元动作单元关键质量特性与影响因素之间的关联矩阵和元动作单元性能耦合矩阵。文献[11]～[13]对蜗杆模型及机器人基础部件进行了静力、模态分析，得到相应的应力变形分布情况以及前10阶固有频率和振型。预测出部件车架的薄弱部位，对研究其可靠性具有重要意义。赵培[14]通过对砂轮架主轴系统建模方法的分析,建立了砂轮架主轴的有限元模型。Wei等[15]将理论计算值与仿真结果进行对比得出误差小于10%，对齿轮啮合传动进行仿真分析，可以直接确定齿轮接触应力的分布情况。文献[16]～[18]对床身、活塞、加工中心进行了静态和模态分析,得到了等效应力、固有频率和振型，分析结果为其研究提供了参考和依据,指出了结构刚度的薄弱环节，为薄弱部分填厚的结构优化设计打下了基础。上述文献通过研究某一基础部件来分析其性能，具有一定的实际意义，但在基本单元中，如何从元动作构成及装配结合面处研究其性能，需要进一步研究。

综上分析，本文拟从机械整机到元动作映射分析入手，在链接功能、链接部位、链接方式要素支撑下，利用三维映射得到元动作单元基本模型。运用有限元分析软件，选取实际装配行为的过盈装配接触压力参数对元动作单元装配结合处进行分析，再通过实验验证的方法，对元动作单元的装配薄弱处提出控制措施。

1 整机到元动作映射模型

文献[19]对构成数控机床的层次模型进行了研究，按照“产品—功能—行为—结构”的层次关系将数控机床分解至简单的结构。由于数控机床的可靠性依赖于机床零部件之间运动的协调配合，因此在数控机床可靠性的研究中，需要一种新的分解方法，该方法不仅要考虑机床的物理结构，还要充分考虑机床的功能和运动，并能将整机分解到足够小的结构单元。本文从整机功能到元动作层面建立三维映射模型，如图1所示，该模型能更好地针对链接功能、链接部位、链接方式进行分析，探索其相互之间的影响。

图1 整机-元动作的三维映射模型

从整机功能到元动作单元的映射采用三维映射法，在元动作三维映射中，元动作应包含所有能实现其功能的构件，各构件应相对独立且具有较高的功能相关性。元动作在加上动力源后能进行独立的运转与试验。与传统的分解方法相比，三维映射模型突出了功能、运动、元动作之间的关系。

2 蜗杆元动作三维模型

根据映射模型提取出本文研究的蜗杆元动作形成元动作装配单元。元动作装配单元是指在装配过程中，由一个实现元动作的基准件为装配基础，可以独立组装达到规定的尺寸链与元动作技术要求，并能够实现该元动作的一组零件组成的独立组件[20]。蜗杆元动作装配单元主要由电机、联轴器、支座、轴承、蜗杆等构件组成。电机与蜗杆之间通过联轴器链接，T型轴承支座支撑蜗杆，电机为整个元动作单元提供动力。在保证链接刚度和质量分布正确的前提下，采用SolidWorks建成蜗杆元动作单元三维实体模型，如图2所示。

图2 蜗杆元动作三维实体模型

3 蜗杆元动作有限元模型分析

ANSYS Workbench可以接受多种格式的数据模型导入，例如:Parasolid格式、IGES格式等。运用ANSYS Workbench能与三维设计软件进行很好的链接，为了提高分析精度没有对模型进行参数简化，将蜗杆元动作单元的实体模型直接导入到有限元分析软件中进行分析计算。

3.1 定义蜗杆元动作的材料属性

联轴器和支座的材料与蜗杆一致，蜗杆元动作单元所选材料属性见表1。

表1 蜗杆元动作单元的材料属性

3.2 网格划分

网格划分是有限元前处理中很重要的步骤，它直接影响着后续数值计算分析结果的精确性。为使网格划分顺利进行，考虑有限元分析的速度与精度，本文定义划分质量为Medium，定义划分方法为自动网格划分，降低了网格划分的难度，提高了效率。蜗杆元动作网格划分如图3所示。

图3 蜗杆元动作网格划分

3.3 约束条件

根据实际情况，确定电机传递到蜗杆元动作单元上的平均转速为11 r/min，同时对蜗杆施加约束，以约束各个方向的自由度。具体施加时，首先选择轴承支座进行位移约束，即将轴承支座当作结构的定位位置。轴承与轴承支座、轴与联轴器、联轴器与电机有装配约束。轴承与轴之间有过盈装配压力，文献[21]中将轴承内圈与轴简化为弹性厚壁圆筒，使用弹性力学的方法得出了装配接触表面压力p的理论计算公式：

(1)

式中：I为直径过盈量；D为轴承内孔直径；D1为轴承内圈直径；D2为主轴内径；E1和μ1分别为轴承内圈弹性模量和泊松比；E2和μ2分别为主轴的弹性模量和泊松比。经计算靠电机端为0.138 50 N，远离电机端为0.087 25 N。依据计算结果对蜗杆元动作单元施加扭矩。

3.4 蜗杆元动作单元静力分析与模态分析

利用有限元分析软件ANSYS Workbench对蜗杆元动作模型进行计算，得到了蜗杆元动作的应力图和结构变形图，如图4、图5所示。

由图4、图5可以得出，蜗杆元动作的最大总变形为0.121 21 mm，发生在电机末端，最大应力为59.011 MPa，主要集中在蜗杆与联轴器的连接处，说明蜗杆轴与联轴器的接合面处为装配薄弱处。

图4 蜗杆元动作应力图

图5 蜗杆元动作结构变形图

利用有限元软件分析出蜗杆元动作单元的前6阶固有频率和振型，蜗杆元动作单元各阶固有频率见表2，各阶模态振型图如图6所示。

图6 前6阶模态振型图

表2 蜗杆元动作单元前6阶固有频率 单位：Hz

通过分析各阶振型图可知，蜗杆元动作的各阶模态图主要区别在于振动幅度大小与振动方向的不同。其中第6阶振动幅度最大，说明蜗杆元动作的频率为1 165.6 Hz时，振动幅度将超标，因此在进行试验时应进行充分的固定约束。

4 蜗杆元动作单元性能验证实验

典型的元动作装配单元包括支撑件、动力源、执行件、中间传动和紧固件5部分。元动作单元构成模型如图7所示。蜗杆元动作单元试验台如图8所示。

图7 元动作单元模型结构

图8 蜗杆元动作单元试验台

试验采集到的蜗杆元动作单元正常工作转速如图9所示，蜗杆元动作单元运行平稳。非正常工作转速如图10所示，蜗杆与联轴器的结合面处有故障时转速波动幅度最大。

图9 正常工作转速

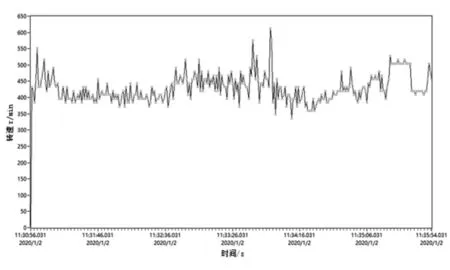
图10 非正常工作转速

通过试验分析可得，蜗杆与联轴器的结合面处是整个蜗杆元动作单元装配薄弱处。试验结果与有限元分析结果相吻合，为此针对蜗杆转动元动作装配单元薄弱处提出以下装配控制措施：

1)轴承与支座要连接可靠，配作卡环弹性挡圈。

2)轴承径向高度要一致，保证蜗杆轴心与轴承回转中心的同轴度。

3)轴承与蜗杆之间的配合间隙要适当，并应计算其接触压力。

4)蜗杆与联轴器之间选择适合的联轴器进行充分连接。

5 结束语

本文建立了整机到元动作单元的三维映射模型及蜗杆元动作单元的实体模型。利用ANSYS Workbench进行了静力分析与模态分析，得出蜗杆元动作的最大总变形发生在电机末端，最大变形量为0.121 21 mm，最大应力主要集中在蜗杆与联轴器的连接处，最大应力值为59.011 MPa。蜗杆与联轴器的接合处为元动作装配单元的薄弱处。试验验证有限元分析结果是合理的，最后提出了装配单元薄弱处的控制措施。