钢轨伸缩调节器对地铁钢桥动力效应影响研究

肖治群

(1.中铁第四勘察设计院集团有限公司 湖北武汉 430063；2.铁路轨道安全服役湖北省重点实验室 湖北武汉 430063)

1 引言

随着我国城市轨道交通的迅速发展，在特殊情况下，为了降低工程造价，有时需要将地铁线路建设于桥梁上，并铺设桥上无缝线路[1]。对于钢桁梁桥等大跨度桥梁，在温度荷载的作用下往往会导致钢轨内部温度应力增加，严重时会使钢轨位移超限甚至断轨，因此需要在地铁钢桥上布设钢轨伸缩调节器，以缓解温度应力等附加应力对桥上无缝线路的影响[2－3]。

目前，对于钢轨伸缩调节器的影响，现有学者往往采用有限元或者解析算法进行研究，并偏重于钢轨伸缩调节器对钢轨应力与位移的影响研究。段翔远[4]采用有限元静力学分析的方法，研究了钢轨伸缩调节器对有砟轨道桥上道岔的影响，表明钢轨伸缩调节器的设置可以保证桥上无缝道岔的稳定性。吕关仁[5]以现场实测的方式，对京沪高速铁路黄河特大桥在钢轨伸缩调节器设置条件下，钢轨的位移变化进行了试验与分析。郭辉等[6]通过对高速铁路大跨度钢桥梁端伸缩装置进行设计研究，以静力验算的方法提出了设置钢轨伸缩调节器的重要性。高洪涛等[7]基于沪昆客专湘江特大桥无砟轨道设计与施工背景，分析并提出了在此线路曲线地段铺设钢轨伸缩调节器的重要性和必要性，并验证了该区域使用钢轨伸缩调节器的安全性与可行性。曾志平等[8]通过现场实测的方式，对跨兴闫公路桥钢轨伸缩器的动力特性进行了现场实测，分析了钢轨伸缩调节器设置后不同行车速度条件下车辆与轨道的动力学效应。

通过现有文献分析可见，对于钢轨伸缩调节器的研究主要集中于钢轨伸缩调节器的设置对于钢轨的静力安全检算以及钢轨累积位移数据的采集，而对钢轨伸缩调节器对车辆－轨道系统动力效应的研究较少，尤其对于地铁钢桥列车动力效应的影响方面尚无相关研究。

鉴于此，本文以道庆洲跨江大桥为例，通过建立地铁列车－轨道－钢桥耦合动力学模型，分析了列车以80 km/h、100 km/h和120 km/h三种速度通过桥梁时，设置钢轨伸缩调节器与不设置钢轨伸缩调节器两种工况下车体加速度以及不同激励条件下的轮轨垂向力，进而对地铁列车行车安全性进行了评估，同时通过提取钢轨伸缩调节器处结构的不同节点的动力响应值，对梁端结构的动力响应进行研究，并对结构动力响应随速度与梁缝间距的变化规律进行了探索。

2 基本结构与设计方案

道庆洲跨江大桥长2.7 km，为钢桁组合梁，桥跨布置为85 m＋85 m＋(121＋276＋121)m主桥＋7×85 m＋7×85 m＋2×85 m＋84 m＋73 m钢桁结合梁。主桥采用主跨276 m的变高度预应力钢桁结合梁方案，跨径组成为(121＋276＋121)m。公路桥面采用钢－混组合结构，标准桁高9.5 m，主墩处桁高为23 m。主墩处变桁高区段下弦杆采用钢－混组合截面，以提高结构刚度，控制钢结构截面尺寸。上层公路桥面宽度31 m，下层轻轨桥面采用正交异性整体钢桥面系[9－10]。桥式布置见图1。

图1 道庆洲跨江大桥立面布置(单位:m)

3 动力分析模型与参数设置

3.1 轨道及钢轨伸缩调节器模型

隔振垫减振型轨道结构采用“梁－体”模型，钢轨采用自定义截面梁单元，可用于模拟钢轨拉、压、弯、扭等变形；扣件采用垂向弹簧单元，用于模拟扣压件和轨下支撑胶垫的综合节点刚度和阻尼；道床采用三维实体单元模拟；隔振垫采用弹簧模拟。本模型采用有限元方法建模，钢轨为60 kg/m；轨枕布置为1 667根/km；弹性扣件刚度为35 kN/mm，阻尼为0.075 kN·s/mm；道床板长度取6 m，厚度为0.28 m，宽为2.8 m，采用C40混凝土，弹性模量取为34 000 MPa；隔振垫刚度为0.025 N/mm。由于模型中三块道床板长度相同，并且道床板间均留有20 mm伸缩缝，缝间填充弹性材料，模型中采用弱弹簧模拟。对梁端轨道结构，钢轨、钢梁、轨枕、钢枕结构均采用梁单元建模，扣件采用弹簧建模。钢轨伸缩调节器的间隙设置在梁端处，如图2所示。

图2 梁端轨道结构与钢轨伸缩调节器模型

3.2 地铁列车－减振垫无砟轨道－钢桁桥耦合动力学模型

本文为了更好地分析地铁列车－减振垫无砟轨道－钢桁桥耦合动力响应，以全桥为基础，采用地铁B2型车，轴重14 t，并考虑桥梁的预平衡区以及动力响应记录区段，如图3所示。利用所建立的仿真分析模型，模拟列车以80 km/h、100 km/h和120 km/h三种等级的速度通过桥梁时，设置钢轨伸缩调节器与不设置钢轨伸缩调节器两种工况条件下车辆和轨道的动力响应。

图3 列车运行示意

4 钢轨伸缩调节器对系统动力响应的影响分析

4.1 地铁列车行车安全性分析

本文模拟了列车以80 km/h、100 km/h和120 km/h三种速度通过桥梁时，设置钢轨伸缩调节器与不设置钢轨伸缩调节器两种工况下车体垂向加速度、轮轨垂向力等指标变化情况，其中轨下垫层刚度选取0.025 N/mm。列车速度为100 km/h时，设置钢轨伸缩调节器与不设置钢轨伸缩调节器两种工况下车辆的动力响应指标车体加速度如图4所示，不同激励条件下列车速度100 km/h时轮轨垂向力响应波形对比如图5所示。

图4 列车速度100 km/h条件下车辆动力响应波形对比

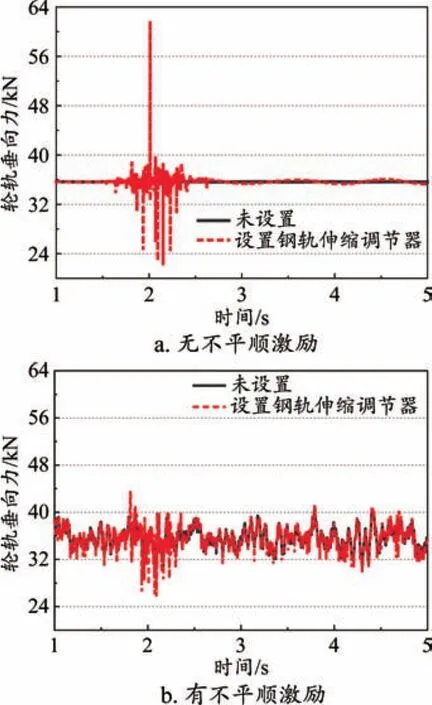
图5 不同激励条件下列车速度100 km/h时轮轨垂向力响应波形对比

由图4～图5可知，车体加速度在设置钢轨伸缩调节器前后变化不大，设置钢轨伸缩调节器和不设钢轨伸缩调节器相比，设置钢轨伸缩调节器对车辆动力学性能影响在无轨道不平顺时较为明显。轮轨垂向力在设置伸缩器工况下，均有增大的趋势(主要表现在进入钢轨伸缩器区段和离开两个阶段)，但当施加轨道不平顺后，轮轨垂向力在有无伸缩器的情况下差异减小。实际列车运行中，轨道存在一定的几何不平顺，故可以认为在轨道不平顺的激励下，钢轨伸缩器对车辆运行品质的影响力会大大下降。

列车以80 km/h、100 km/h和120 km/h三种速度通过桥梁时的车体加速度与轮轨垂向力最大值见表1。设置钢轨伸缩器后，三处钢轨垂向位移与未设置前比较基本不变。设置钢轨伸缩调节器对中间点钢轨垂向加速度影响较大，左右端点的影响相对较小，但均在限值范围以内[11－12]。

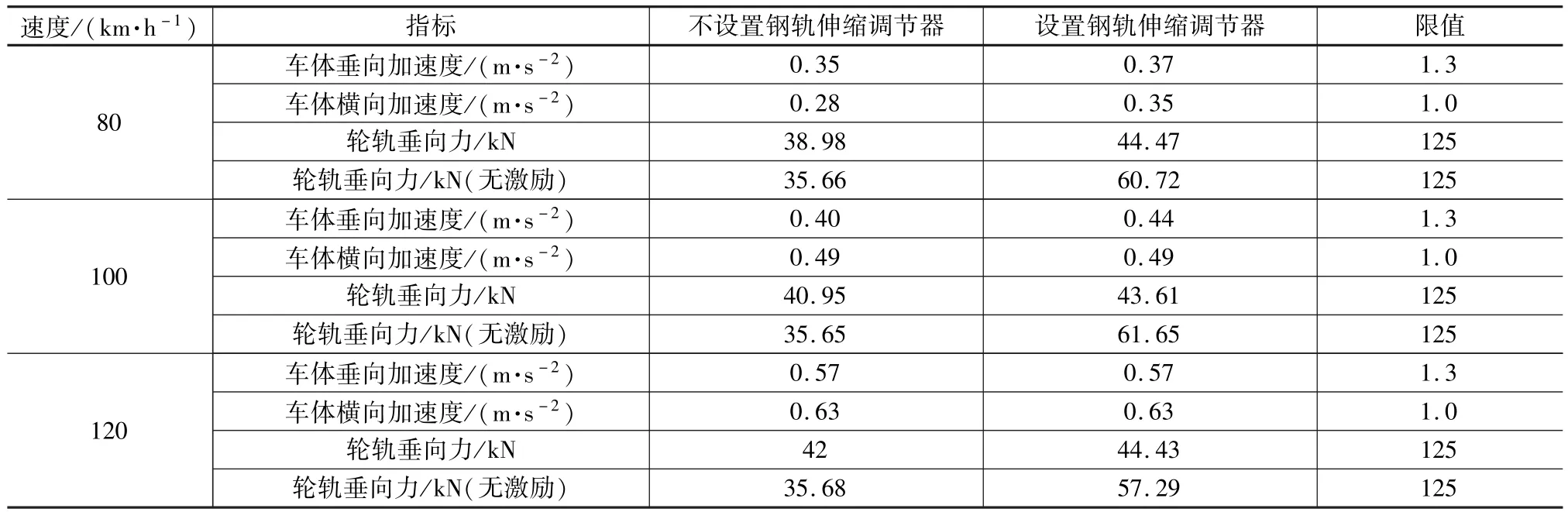
表1 车体垂向加速度与轮轨垂向力最大值汇总

由表1结果可知，设置钢轨伸缩调节器和不设钢轨伸缩调节器相比，设置钢轨伸缩调节器对车辆动力学性能的影响在无轨道不平顺时较为明显。轮轨垂向力在设置伸缩器工况下，均有增大的趋势(主要表现在进如钢轨伸缩器区段和离开两个阶段)，但当施加轨道不平顺后，车体加速度和轮轨垂向力在有无伸缩器的情况下差异减小，对车辆动力学性能指标几乎没有影响。通过相关规范可知，设置钢轨伸缩调节器后，行车舒适性指标和行车安全性指标均在限值范围内，所以行车舒适性和安全性均满足要求。

4.2 结构动力响应随速度的变化规律

为了研究钢轨伸缩调节器梁缝区域的结构受力与变形随速度变化规律，设钢轨伸缩调节器的梁端调整间距为1 000 mm，提取在80 km/h、100 km/h、120 km/h行车速度下钢轨、钢枕、纵向钢梁、扣件支点处的动力响应进行对比分析。不同行车速度作用下各节点钢枕垂向位移时程曲线如图6所示。

图6 不同行车速度下钢轨节点1垂向位移时程曲线

由图6的钢轨垂向位移幅值可知，不同车速下，同一节点的垂向位移变化幅值差异不大。不同节点的位移响应波形较接近，其中120 km/h时钢轨位移幅值最大，随着距离梁端间隙距离的增大，钢轨节点幅值逐渐减小。

5 结论

本文以钢轨伸缩调节器为研究对象，通过建立地铁列车－轨道－钢桥耦合动力学模型，对列车以不同速度通过钢桥时的车－轨－桥耦合动力效应进行分析，并得出了以下结论:

(1)车体加速度在设置钢轨伸缩器前后变化不大，轮轨垂向力在设置伸缩调节器后，均有增大的趋势(主要表现在进入钢轨伸缩器区段和离开两个阶段)，但当施加轨道不平顺后，钢轨伸缩调节器的影响会被掩盖，可以认为钢轨伸缩调节器对于列车实际运营状况下的安全平稳性影响较小。

(2)钢轨伸缩调节器结构对于缓解梁缝位置处的钢轨变形具有一定的作用，且该作用随着梁缝长度增大而变得更加显著。

(3)整体而言，梁缝位置的钢轨伸缩调节器为主要受力结构，依然对桥梁上的钢轨、扣件、纵向钢梁以及悬吊的钢枕在受力方面有一定辅助作用。