基于Ansys Workbench的正交异性钢桥面疲劳性能分析
高 明
(中铁十六局集团第三工程有限公司 浙江湖州 313000)
1 引言
正交异性钢桥面具有自重轻、整体性好、承载能力大、行车舒适性好的特点,在现有的铁路和公路桥梁中被广泛应用。然而正交异性钢桥面连接形式复杂且连接位置较多,承受循环应力作用的钢桥面容易产生疲劳裂缝或出现完全断裂等现象,国内外许多钢桥的桥面板已出现不同程度的疲劳开裂[1-2]。于1961年建成的Haseltal桥在投入运营后不久出现了疲劳裂纹。1966年英国建成的Severn桥,在运营十年后在大桥主梁上发现了三种不同形式连接细节的疲劳裂纹。韩国圣水大桥由于车辆超载、疲劳等原因,导致该桥在竣工通车15年后垮塌的悲剧。美国的Silver Bridge在运营39年后某天上班高峰时靠近俄亥俄州一端的C13号系杆连接处发生断裂,导致该桥倒塌[3]。我国正交异性钢桥面板的桥梁中疲劳开裂事故也时有发生,如2001年位于四川省宜宾市的南门大桥吊杆及桥面板部分断裂事故,以及1997年建成的虎门大桥于2003年开始不断出现疲劳裂纹以及纵向裂缝[4]。
疲劳问题一直是正交异性钢桥面研究的热点[5-7]。因铁路桥梁荷载更大、列车运行时速度更快,桥梁所受冲击状态更为复杂。列车经过时,正交异性钢桥面各部位的影响线长度短,同一部位可能会产生多次应力循环。高速铁路上的桥梁,正交异性钢桥面所承受的运营列车次数增多,导致构件反复应力的循环次数增多。所以更应该关注铁路桥梁正交异性桥面板的疲劳问题。
研究正交异性钢桥面的疲劳问题,通常采用试验法进行,一般是一桥一试验。疲劳试验一般采用的大型试件是正交异性钢桥面真实尺寸的一部分,如在捷克进行的疲劳试验试件,见图1a,或者缩尺模型试件,如英国运输和道路研究试验所(TRRL)对主跨998 m的塞文桥钢桥面进行了疲劳试验研究[8],见图1b。试件包括桥面、横梁和2条纵肋,试件构造和试验荷载等。

图1 国外疲劳试验试件(单位:mm)
通过研究正交异性钢桥面的构造细节,得到纵向U肋与横梁接缝的疲劳强度及疲劳裂缝形式,并针对其结果提出维修和改进方法,同时研究了足尺模型和缩尺模型试件疲劳强度的差别[9-10]。
在国内,铁道科学研究院[11]对昂船洲大桥进行了肋与桥面板焊接连接的足尺尺寸试样的疲劳试验研究,见图2。研究结果表明:试样的疲劳裂纹大都出现在桥面板内侧的焊根和外侧的焊趾处,跟实际桥梁的疲劳裂纹相似。
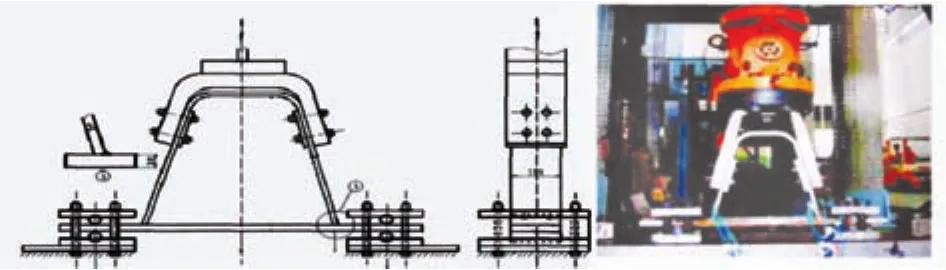
图2 铁道科学研究院昂船洲大桥疲劳试验试件
对苏通大桥正交异性钢桥面板典型的焊接构造细节进行了疲劳试验,见图3。研究结果表明:正交异型钢桥面横梁受力比较复杂,在端部和纵肋焊接位置出现裂纹;纵梁与顶板连接处的疲劳损伤较大,疲劳破坏位置位于焊缝构造处,发生在纵肋外侧的桥面板母材上。
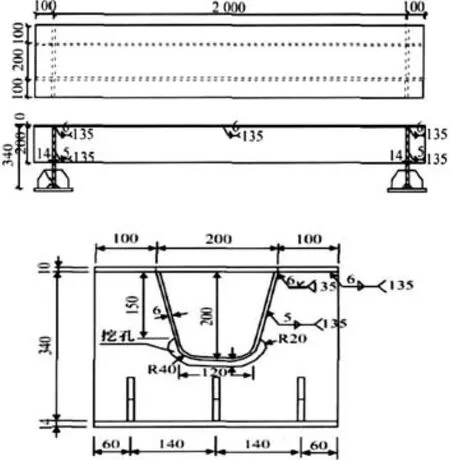
图3 苏通大桥疲劳试验试件(单位:mm)
通常疲劳试验受限于试验规模、试验成本、试验周期以及试验结果说服力不足等因素,而采用有限元法分析正交异性钢桥面的研究也不多,因此,通过疲劳有限元分析的方法,可有效克服以上限制因素。本文采用有限元分析软件Ansys Workbench进行疲劳有限元分析计算。
2 Ansys Workbench疲劳有限元分析
Ansys Workbench是一款业界领先的工程仿真技术集成平台软件。采用Ansys Workbench疲劳分析软件进行疲劳分析[12],一般先将有限元模型进行线性静力分析,在这个过程之后,有限元软件Ansys Workbench通过设计仿真自动读取相关应力求解结果;然后添加疲劳工具条,设置需要求解的结果。对疲劳工具的添加,无论在求解之前还是之后,对结果均不会影响,因为疲劳计算并不依赖应力分析计算。采用Ansys Workbench进行疲劳分析,需经历如图4所示的流程完成一次疲劳分析过程。
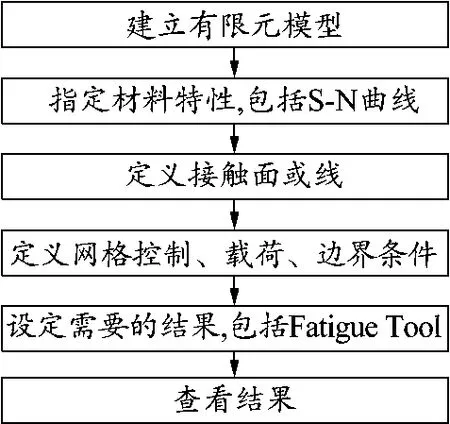
图4 Ansys Workbench疲劳分析流程
疲劳材料特性的定义需要输入常规的杨氏模量、泊松比以及应力相关的强度数据和极限数据等;进行疲劳分析还需要定义材料的S-N曲线数据,材料的S-N曲线是用来说明外加应力水平与标准试件疲劳寿命之间关系的曲线,是疲劳分析不可缺少的一步。程序中对于不同的平均应力或应力比,若单S-N曲线材料数据适用,则多重S-N曲线同样可以使用。
载荷与边界条件,载荷的加载方式和结构的边界支撑条件对疲劳分析结果影响较大,在确定载荷的加载方式和结构的边界支撑条件时,应尽量与实际情况相符合。
进行疲劳计算时,需要插入疲劳工具条,设定需要考察的疲劳结果,这里设定的疲劳结果包括疲劳寿命、疲劳损伤、安全系数等。
不同的求解组合可以与疲劳工具相结合使用,针对环境的多重组合情况,将在不同环境的线性组合结果上进行疲劳计算。
3 正交异性钢桥面疲劳试验实例
本文引用中南大学土木工程学院叶梅新、罗如登课题组针对多座高速铁路和高速公路钢桥正交异性钢桥面疲劳理论分析和试验研究成果,对研究中制作的编号为A-1的正交异性钢桥面模型疲劳试验试件采用Ansys Workbench进行疲劳有限元计算,将电算结果同疲劳试验结果进行对比分析。A-1试件和疲劳试验结果见图5。A-1试件由翼板、4个U肋、横梁和支座垫块组成。试件总长3 000 mm、宽300 mm、高500 mm。U肋高 260 mm,上宽 300 mm、下宽184 mm。试件面板厚度、U肋尺寸、横梁顶底板厚度以及横梁腹板厚度均与实桥相同。试件材料采用与实桥相同的Q370qD钢及相应焊条。从试验记录和图5可知,疲劳荷载循环次数在75万次之前,试件未出现裂纹,仍处于弹性变形阶段。在75万次时试件开始出现第1条裂纹,之后裂纹逐渐增多;到160万次时,共出现9条裂纹,顶板断裂,试件破坏,停止试验。
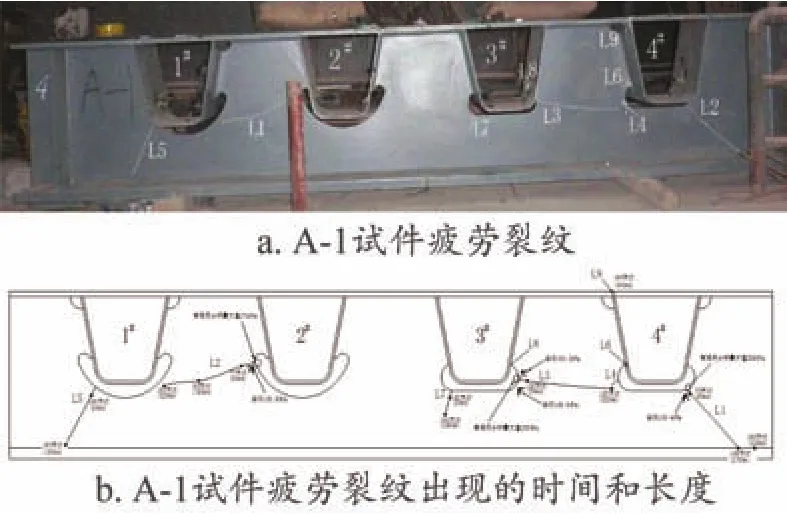
图5 正交异性钢桥面模型疲劳试验A-1试件
4 正交异性钢桥面疲劳性能有限元分析
4.1 建立有限元疲劳分析模型
A-1试件立面、侧面、加载和支撑见图6。

图6 A-1试件和有限元模型(单位:mm)
其中,1号、2号下部开孔为苹果形,3号、4号U肋与横梁腹板连接下部开孔为平底形;1号、4号U肋所在翼板、U肋、横梁腹板三者连接处的横梁腹板开孔,2号、3号U肋在该处先开孔,焊接后再将孔填充。模型中,在U肋与顶板、U肋与横梁腹板焊接处,对模型网格进行细化。钢材的弹性模量E=210 GPa,泊松比μ=0.3,屈服强度370 MPa,抗拉强度510 MPa。钢材疲劳性能试验数据见表1。

表1 桥梁结构Q370qD钢疲劳性能试验数据
参考文献[13],通过试验研究桥梁结构Q370qD钢制作的双金属板,采用对接接头的疲劳性能,并通过数理统计计算,获得50%和97.7%两个置信度下试验材料的S-N曲线,并确定2×106次循环下的疲劳强度。根据表1中的试验数据,可得到本文模型材料所对应的S-N曲线。
顶板中心处施加随时间变化的正弦函数荷载,最大荷载Pmax=270 kN,最小荷载Pmin=20 kN,荷载幅为ΔP=250 kN。
4.2 静力荷载有限元分析
图7为A1试件有限元分析结果云图。由图7a可知,等效平均应力最大值为328.85 MPa,出现在3号U肋下部腹板处;1号、2号和4号U肋各自的最大平均等效应力也均出现在U肋下方腹板开孔处,这些部位在后续进行疲劳性能分析时,应更多关注。由图7b可知,当荷载增大至270 kN时,整个结构的最大位移为1.79 mm。
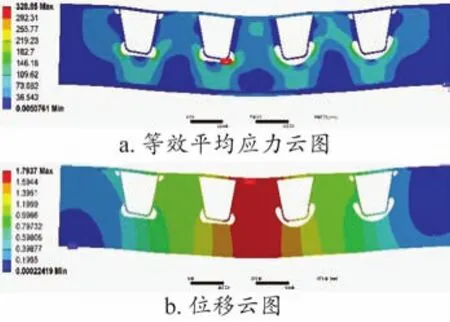
图7 A1试件有限元分析结果云图
4.3 疲劳荷载有限元分析
添加疲劳工具Fatigue Tool,这里需要考虑平均应力对S-N曲线结果的影响。Ansys Workbench Fatigue Tool提供了多种平均应力修正理论供研究者选择,如Goodman平均应力修正理论、Soderberg平均应力修正理论、Gerber平均应力修正理论。考虑到实际试验用材料为韧性材料,因此选用Gerber平均应力修正理论。
考虑到还有其他一些因素对S-N曲线的影响(荷载形式、尺寸效应、表面光洁度、表面处理、温度和环境等),将这些影响因素可集中体现在疲劳强度(降低)因子Kf中,通常取疲劳强度因子为0.8。选择疲劳寿命、疲劳损伤、安全系数作为分析结果。
图8为A1试件Ansys Workbench疲劳分析结果。本模型寿命最危险位置在3号U肋下部开孔处,理论计算寿命约为73.08万次,与试验试件出现疲劳裂纹的次数相近;在给定200万次设计寿命下失效的安全系数为0.746,设计寿命与可用寿命的比值最大值为2.736 5。

图8 A1试件Ansys Workbench疲劳分析结果
4.4 疲劳有限元分析结果与疲劳试验结果对比
通过对比疲劳有限元分析结果与疲劳试验结果可知:疲劳试验中,第一条疲劳裂纹L1出现时所对应的荷载循环次数约为75万次,发生在4号U肋下方横梁腹板平底形开孔处,第二条疲劳裂纹L2出现时所对应的荷载循环次数约为77万次,发生在2号U肋下方横梁腹板苹果形开孔处。考虑到疲劳裂缝出现的随机和离散性,可以认为这两个位置基本是同时出现疲劳破坏。
疲劳有限元分析结果的疲劳寿命最小荷载循环次数约为73万次,基本与疲劳试验结果吻合,但首次出现裂纹的位置在3号U肋下方的横梁开孔处,而在疲劳试验中,该位置出现的是第七条裂纹L7,荷载循环次数约为153万次。这说明疲劳有限元分析能够依据等效应力的大小较好地预测疲劳寿命,但由于实际的疲劳破坏具有随机和离散性,所预测的首次疲劳破坏位置不一定准确。
5 结论
(1)疲劳有限元分析计算的最小疲劳寿命约为73.08万次,与疲劳试验最先出现疲劳裂缝的荷载循环次数75万次接近,说明本文疲劳有限元分析方法和计算参数对模拟疲劳计算是可行的。
(2)疲劳有限元分析计算结果揭示的疲劳寿命最危险位置和疲劳试验得出的首次疲劳破坏位置不一致,这可能是由于实际的疲劳破坏具有随机和离散性所导致。
(3)U肋下方腹板平底形开孔最早在75万次荷载循环时出现疲劳裂纹,苹果形开孔最早在77万次荷载循环时出现疲劳裂纹,说明开孔形状对试件的疲劳性能影响不大。

