超弹性SMA唯象本构模型及其在震动控制中的应用

刘 博

(中铁二十局集团有限公司 陕西西安 710016)

1 引言

结构振动控制技术能够有效抑制结构在地震作用、风振作用和爆破作用等外部激励下的响应和损伤积累，提高结构的抗灾变性能，是一种积极有效的工程结构防振(震)减灾措施[1－2]。形状记忆合金(Shape Memory Alloy，SMA)作为性能优良的智能感知、驱动功能材料，具有可恢复应变大、与其他基体耦合难度低以及耐腐蚀性能好等优点。工程领域的诸多专家和学者试图利用SMA的超弹性特性减轻振(震)动带给结构的危害。胡淑军等[3]基于超弹性SMA的自复位性能设计了一种抗震性能良好的SMA支撑，并通过SMA支撑的拟静力试验验证了其自复位能力及耗能能力。阎石等[4]提出了一种新型变形可恢复SMA减震装置，解决了SMA线材的锚固问题，并建立了该新型SMA减震装置的恢复力模型。

为充分发挥SMA基减震装置的减振(震)特性，需建立一个表述简单、相关参量容易获取，且适于实际工程应用的SMA力学模型。经典的SMA力学模型主要分为两类:细观力学本构模型和宏观唯象本构模型[5]。细观力学本构模型表述过于复杂，相关参量不容易测量和确定，距离实际工程应用相差甚远；宏观唯象本构模型基于试验结果来描述SMA的力学响应特性，从工程应用角度来说，更为实用[6]。作为宏观唯象本构模型的典型代表，Graesser-Cozzarelli(G-C)模型因不涉及SMA复杂的微观结构，且定义了适用于实际工程计算使用的宏观参数体系，而在结构振动控制领域得到广泛应用[7]。但G-C模型由于没有相变约束条件，所以无法描述应力诱发马氏体相变结束后马氏体相SMA的硬化特性。

鉴于此，本文首先对G-C模型进行数值仿真，分析各参数变化对超弹性SMA滞回曲线的影响，明确G-C模型存在的不足，指出G-C模型改进方向。然后，通过在G-C模型中引入马氏体硬化项，描述超弹性SMA在大应变幅值工况下的应力－应变关系，并对超弹性SMA滞回曲线进行数值模拟，验证模型的有效性。最后，借鉴机械领域的齿条齿轮加速器，设计一种具有自复位功能的位移放大型SMA减震装置，并以一个自复位SMA减震装置控制的框架结构为例，探讨本文建立的超弹性SMA唯象本构模型在工程结构被动减震控制领域的应用价值。

2 G-C宏观唯象本构模型

2.1 G-C模型概述

Graesser和Cozzarelli等在经典Bouc-Wen模型[8]的基础上，建立了一种相对简单并且比较实用的本构模型，其增率形式的表达式为:

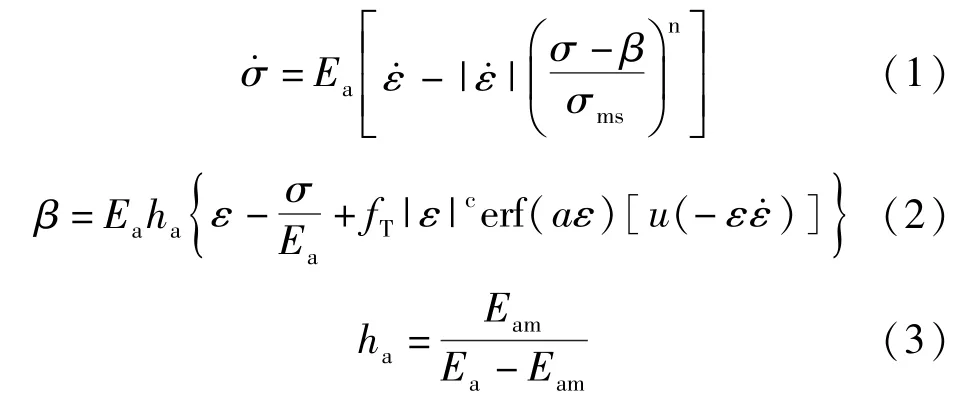
式中:σ为应力；ε为应变；Ea为变形模量；Eam为非弹性变形模量；β为背应力；σms为屈服应力阈值；c、a、n为控制SMA滞回曲线形状的材料参数；ha为控制SMA滞回曲线在非弹性范围内斜率的常数；fT为描述不同温度下SMA状态的参量，当fT＝0时，G-C模型退化为经典的Bouc-Wen模型；erf(x)和u(x)分别为误差函数和单位阶跃函数，误差函数erf(x)可保证卸载后逆相变完成时残余应变为零，其表达式为:

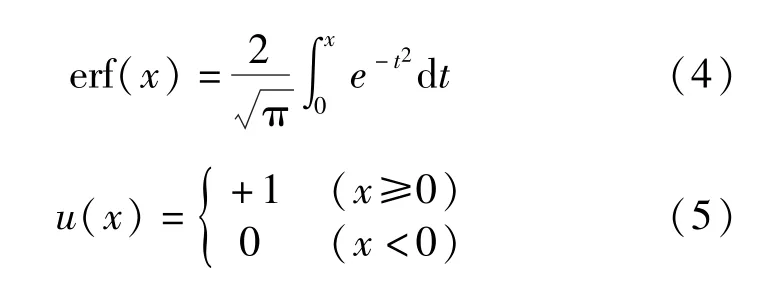
2.2 超弹性SMA迟滞曲线仿真

依据G-C模型，通过Matlab中Simulink模块对超弹性SMA迟滞曲线进行数学仿真。图1为0.1 Hz频率、2%应变振幅加载条件下，各参数对超弹性SMA迟滞曲线的影响，相关仿真参数见表1。由图1a可知，超弹性SMA迟滞曲线的尺寸及卸载段平台高度对参数fT较为敏感，随着fT的增大，迟滞曲线卸载段平台不断增高，而迟滞曲线尺寸不断减小；由图1b可知，参数a对SMA迟滞曲线形状有较大影响，参数a越小，超弹性SMA迟滞曲线越饱满，形状越接近“梭形”；由图1c可知，当参数c小于0.01时，迟滞曲线的形状对该参数不敏感。

表1 超弹性SMA迟滞曲线的仿真参数值

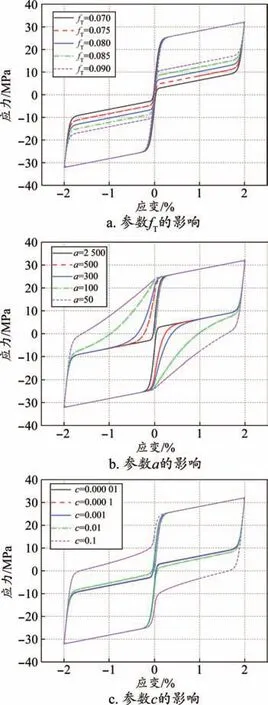
图1 G-C模型中各参数对超弹性SMA迟滞曲线的影响

2.3 G-C模型的不足

通过上述G-C模型的参数分析，可以明确G-C模型存在3点不足:(1)模型没有相变约束条件，无法描述应力诱发马氏体相变结束后马氏体相SMA的硬化特性；(2)erf(x)中被积函数没有原函数，不能使用牛顿—莱布尼兹公式求解，只能做近似计算；(3)式(1)中(σ－β)计算结果可能为负值，当n为实数而非整数值时，计算可能无意义。上述G-C模型的不足为下文模型的改进指明了方向。

3 SMA马氏体硬化特性及改进G-C唯象本构模型

3.1 SMA马氏体硬化特性描述

G-C模型由于没有相变约束条件，所以无法描述应力诱发马氏体相变结束后马氏体相SMA的硬化特性。 Wilde等[9]、Zhang等[10－11]和张振华等[12]通过在G-C模型中加入马氏体硬化项，描述了超弹性SMA在大应变幅值工况下的应力－应变关系。本节对上述学者描述SMA马氏体硬化特性的方法进行回顾，并进一步指出相关方法的不足，为下文改进G-C唯象本构模型的建立奠定基础。

Wilde等对G-C模型进行了拓展，考虑了大应变幅值工况下SMA的马氏体硬化特性，模型具体表达式为:

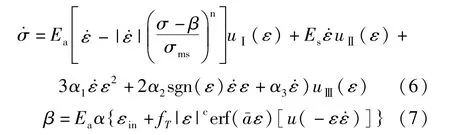
式中，函数uⅠ(ε)、uⅡ(ε)和uⅢ(ε)的表达式分别为:

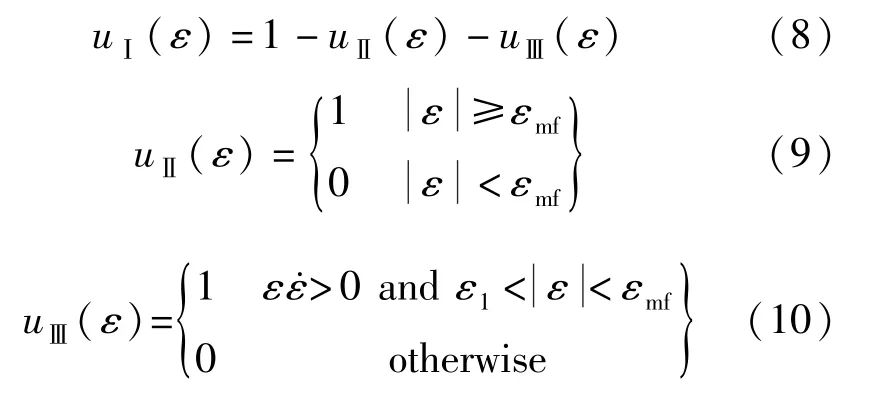
Wilde等将超弹性SMA的恢复力响应通过式(8)～式(10)划分为三部分。当应变超出马氏体相变结束时所对应的应变值εmf后，超弹性SMA恢复力曲线转化为以Es为马氏体硬化段的变形模量。uⅡ(ε)函数的引入使SMA恢复力曲线在向马氏体硬化段转换时更加平滑。虽然Wilde等建立的模型可描述大应变幅值工况下SMA的马氏体硬化特性，但遗憾的是，模型中引入过多不具有物理意义的参数，例如α1、α2和α3，这些参数的合理取值范围不容易被确定。此外，(σ－β)可能为负值，当n为实数而非整数值时，计算可能无意义。

Zhang等在Wilde等建立模型基础上，对应力增率和背应力的表达式进行了修正，修正表达式为:

式中，函数uⅠ(ε)、uⅡ(ε)、uⅢ(ε)、K(ε)和g(t)的表达式分别为:

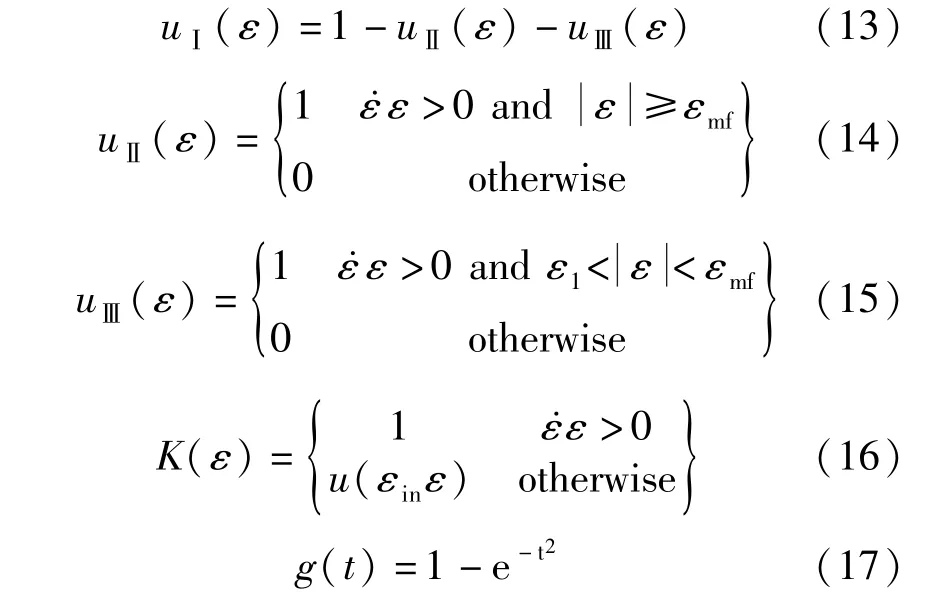
相比于Wilde等建立的模型，Zhang等建立的模型更为稳定，运算速度更快，但超弹性SMA恢复力响应仍然被划分为多个部分，开关标志较多，模型较为复杂。张振华等建立的模型与上述Wilde等以及Zhang等建立的模型类似，同样是通过多个开关部分来描述SMA的马氏体硬化特性，此处不予赘述。需注意，式(6)～式(17)中未解释含义的参数可参见G-C模型。

3.2 改进G-C唯象本构模型的建立

参考上述G-C系列模型，建立一种形式简单且能够描述SMA在大应变幅值下马氏体硬化特性的唯象本构模型，具体表达式为:

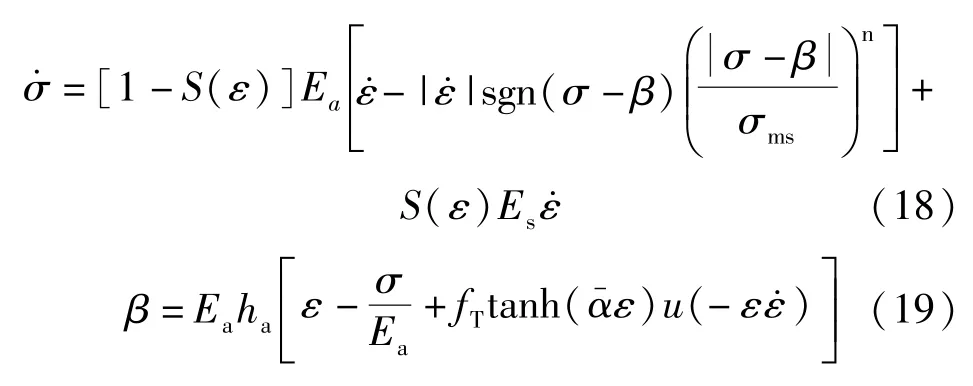
式中:Es为马氏体硬化段的变形模量；εmf为马氏体相变结束对应应变值；其余参数含义与G-C模型相同。

由式(18)～式(20)的表达式可知，本文提出的改进G-C唯象本构模型的应力率和背应力计算公式延续了原始G-C模型的表达形式，并克服了n只能取实数而非整数的限制。为了描述SMA在大应变幅值下的马氏体硬化特性，改进G-C唯象本构模型在应力率计算公式中添加了S(ε)函数，其具体表达式见式(20)。相比于3.1节介绍的模型，本文建立的改进G-C唯象本构模型形式更为简单，各参数物理意义也更为明确。

采用改进G-C唯象本构模型对发生马氏体硬化特性的超弹性SMA单向拉伸应力－应变曲线进行数值仿真，使用的材料参数见表2。图2为0.1 Hz频率、7%应变振幅加载条件下的仿真结果。由图2可知，改进G-C唯象本构模型可以描述超弹性SMA在大应变幅值工况条件下的马氏体硬化特性。

图2 超弹性SMA单向拉伸应力－应变曲线

表2 材料参数

4 改进G-C唯象本构模型的应用

4.1 位移放大型SMA减震装置

本小节借鉴机械领域的齿条齿轮加速器，设计一种具有自复位功能的位移放大型SMA减震装置，构造如图3所示，并以该减震装置控制的单层单跨框架结构为例，对改进G-C唯象本构模型在结构被动减震控制应用中的可行性进行研究和讨论。该减震装置主要包括:闭式防护壳、滑动导杆、连接杆、SMA丝、导向轮、滑块、传动齿轮、六角法兰带齿螺栓。闭式防护壳左右侧壁各有两个六角法兰带齿螺栓；SMA丝固定于六角法兰带齿螺栓和滑块之间；滑动导杆和连接杆与受控结构相连，当受控结构发生变形时，将带动滑动导杆往复运动，滑动导杆产生位移通过传动齿轮传递给滑块，进而带动SMA丝发生变形。为提高SMA耗能性能，本文设计安装于滑动导杆与滑块间的位移放大装置。小齿轮直径r，大齿轮直径R，滑动导杆利用小齿轮带动复合齿轮转动，大齿轮带动滑块发生放大R/r倍的位移。定义R/r为放大系数α，相对滑动导杆、滑块的位移将被放大α倍。

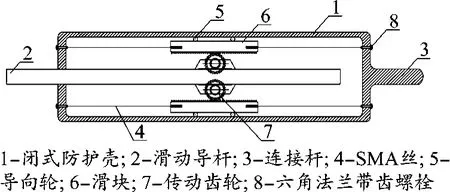
图3 具有位移放大功能的自复位SMA减震装置

该位移放大型SMA减震装置的恢复力FSMA-D可表示为:

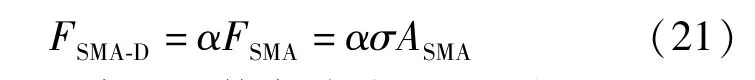
式中:σ为SMA产生的恢复应力，通过改进G-C唯象本构模型计算，材料参数见表2。需注意，在计算该位移放大型SMA减震装置产生的恢复力时，位移通过齿轮系统放大了α倍；ASMA为SMA的横截面面积。在下文的控制算例分析中，将ASMA设置为12.56 mm2，SMA初始长度设置为400 mm，位移放大倍数α设置为2。

4.2 被动减震控制算例分析

图4为位移放大型SMA减震装置控制结构的计算简图。该结构为单层单跨剪切型框架，结构的跨度为1 200 mm，层高为800 mm，质量为200 kg，层间刚度为83 480 N/m，阻尼比为5%。设结构的质量集中在楼板处，且平面内无限刚度的楼板与无限刚度的“人字型”支撑通过位移放大型SMA减震装置串联。输入的地震波为EL-Centro波，其加速度峰值为0.40 g。数值积分时的时间步长取为0.02 s。

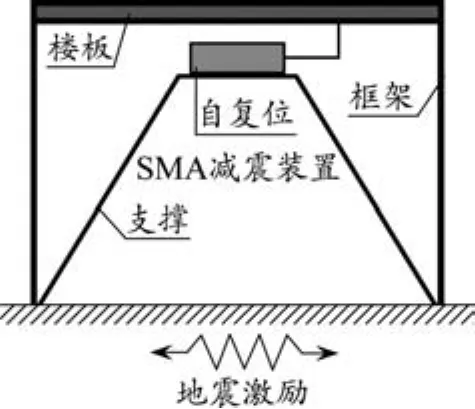
图4 位移放大型SMA减震装置控制结构计算简图

图5a为减震结构在受控与无控状态下的位移响应，可以看出，布置位移放大型SMA减震装置后，结构的层间位移得到了有效控制。受控结构的最大层间位移由32 mm降低为11 mm，减震率高达65.62%。图5b为位移放大型SMA减震装置输出的恢复力曲线，减震装置的输出力呈现出饱满的滞回曲线，而且在地震结束后可以恢复到原状，不产生残余变形。综上可知，改进G-C唯象本构模型具有一定的工程应用价值，该模型可为SMA基减震装置力学性能的数值仿真及其在被动减震控制中的应用提供理论支持。

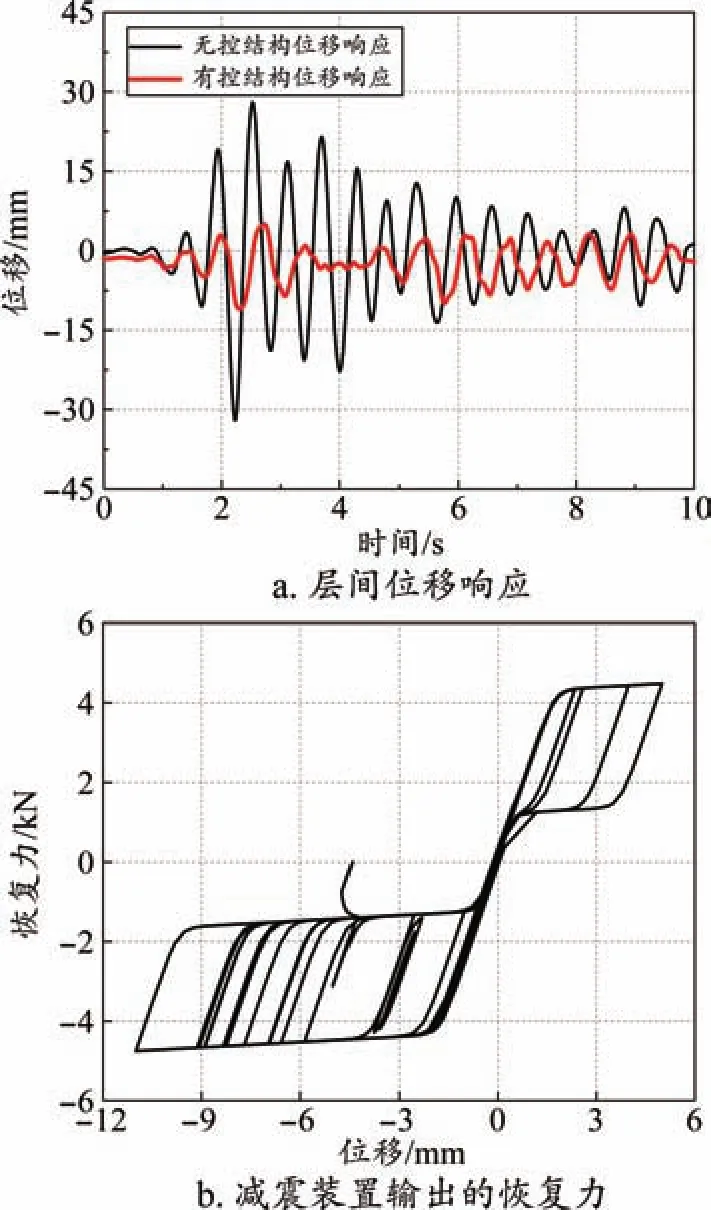
图5 结构被动减震控制分析结果

5 结论

本文在G-C模型参数分析的基础上，建立一种能够描述超弹性SMA在大应变幅值工况下应力－应变关系的唯象本构模型，并将其应用于结构被动减震控制中。得到的结论如下:

(1)改进G-C唯象本构模型可以描述超弹性SMA在大应变幅值工况条件下的马氏体硬化特性。

(2)位移放大型SMA减震装置的输出力呈现出饱满的滞回曲线，而且在地震结束后可以恢复到原状，不产生残余变形。

(3)改进G-C唯象本构模型形式简单、概念明确、参数容易得到，具有一定的工程应用价值，可为SMA基减震装置力学性能数值仿真及其在被动减震控制中的应用提供理论基础。