数形结合 合乎情理

文／李蕴欣

（作者单位：江苏省连云港市海州实验中学）

函数是中学阶段非常重要的知识点，对我们知识的整体把握起着至关重要的作用。初中的函数主要包括：一次函数、反比例函数、二次函数。除此之外，函数思想是我们在初中提高思维能力的重要来源。函数作为历年中考命题的重点考查内容之一，我们做题时如何做到“会而对，对而全”呢？下面，让我们通过对一次函数和二次函数的解读来予以说明。

一、数形结合之一次函数

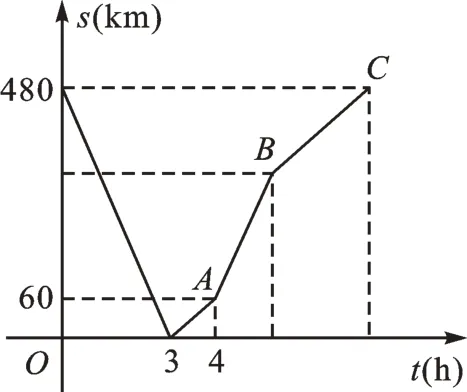
例1（2021·江苏宿迁）一辆快车从甲地驶往乙地，一辆慢车从乙地驶往甲地，两车同时出发，匀速行驶，两车在途中相遇时，快车恰巧出现故障，慢车继续驶往甲地，快车维修好后按原速继续驶往乙地，两车到达各地终点后停止，两车之间的距离s（km）与慢车行驶的时间t（h）之间的关系如图：

（1）快车的速度为________km/h，C点的坐标为________。

（2）慢车出发多少小时后，两车相距200km。

【考点】一次函数的应用，一次函数与一元一次方程的应用。

解：（1）100，（8，480）。

（2）设慢车出发th，两车相距200km。

①若是相遇前两车相距200km，

则60t+100t+200=480，

解得t=。

②若是相遇后两车相距200km，

则60t+100（t-1）-200=480，

∴慢车出发或时，两车相距200km。

【点评】本题是以图像形式考查一次函数的应用，体现数形结合、分类讨论等数学思想，这些思想近年来也一直是中考命题的热点。第（1）问，由图像信息先求出慢车的速度，再根据相遇时慢车走的路程求出快车走的路程，根据速度=路程÷时间求出快车速度，最后根据快车比慢车先到达终点可知C点是慢车到达终点时所用时间。本问解决思路重在对图像的分析，得分的关键是弄清图像拐点的意义。对于第（2）问，我们要分两车相遇前和相遇后两种情况讨论，考虑问题不全面是造成得不到全部分数的主要原因。

二、数形结合、转化思想之二次函数

例2（2021·安徽）已知抛物线y=ax2-2x+1（a≠0）的对称轴为直线x=1。

（1）求a的值。

（2）若点M（x1，y1），N（x2，y2）都在此抛物线上，且-1＜x1＜0，1＜x2＜2。比较y1和y2的大小，并说明理由。

（3）设直线y=m（m＞0）与抛物线y=ax2-2x+1交于点A、B，与抛物线y=3（x-1）2交于点C、D，求线段AB与线段CD的长度之比。

【考点】二次函数的性质，二次函数图像上点的坐标特征。

解：（1）抛物线y=ax2-2x+1（a≠0）的对称轴为直线x=-，则a=1。

（2）由（1）可知，二次函数表达式为y=x2-2x+1。

∵a=1＞0，

∴当x＞1时，y随x的增大而增大，

当x＜1时，y随x的增大而减小。

∵-1＜x1＜0，1＜x2＜2，

∴1＜1-x1＜2，0＜x2-1＜1。

结合函数图像可知，当抛物线开口向上时，距离对称轴越远，值越大，

∴y1＞y2。

（3）联立y=x2-2x+1与y=m（m＞0），

【点评】本题难度适中。同学们应掌握解决类似函数问题所必需的基础能力，比如数形结合思想、如何求函数交点等，否则无法解决基础题，得不到基础分。第（1）问，根据公式，对称轴为直线x=-，代入数据即可。第（2）问，结合函数的图像，根据二次函数的增减性可得结论。第（3）问，分别联立直线y=m（m＞0）与两抛物线的表达式，表示出A、B、C、D的坐标，再表示出线段AB和线段CD的长度，即可得出结论。