气体介质对排气式气囊缓冲特性影响研究
李博,竺梅芳,雷江利,何青松,王飞
北京空间机电研究所,北京 100094
1 引言
缓冲气囊是一种传统的无损着陆缓冲设备,常与降落伞配合应用于无人机回收、火星探测器着陆和载人飞船返回舱回收等方面。1997~2004年,“火星探路者号”“猎兔犬2号”“勇气号”和“机遇号”等火星探测器均采用了缓冲气囊作为软着陆缓冲装置[1-4]。近年来,美国在CEV 载人飞船与Starlines载人飞船的研制过程中发展了适合于这两种飞船的气囊着陆缓冲系统[5-7],2019年 Starliner飞船返回舱成功实现返回着陆,缓冲气囊工作良好。中国在新一代载人飞船试验船研制过程中也发展了一套组合式缓冲气囊[8],并于2020年5月成功软着陆,实现了返回舱的无损回收。
缓冲气囊分为排气式气囊与不排气气囊,如各火星探测器气囊均采用不排气气囊,而地球表面着陆缓冲用气囊,如无人机气囊、飞船返回舱气囊等均采用排气式缓冲气囊[9]。排气式缓冲气囊的工作原理是利用气囊内气体介质的压缩与释放控制气囊内外压差,从而向回收载荷提供支持力,以起到减速效果。这一过程中,气囊内气体介质的特性会对缓冲气囊的缓冲效果造成一定影响。
目前关于气体介质与环境压强对气囊缓冲特性影响的相关研究还较少。文献[10-11]以力学平衡方程和热力学方程为基础,建立了气囊缓冲过程理论分析模型。文献[12]分析了可能影响气囊缓冲特性的气体参数,指出影响不排气气囊缓冲特性的气体参数主要是气体比热容和绝热系数,但其对气体参数对排气式气囊的影响并未进行分析
本文以新一代载人飞船试验船返回舱为研究对象,结合当前航天器无损回收中的工程应用需求,基于流体力学和热力学理论建立了带有内囊的组合式气囊缓冲过程动力学模型,推导研究了气体介质对缓冲过程中囊内气体状态变化及能量耗散的影响机理。为缓冲气囊工程应用中气体介质的选择提供了一定参考。
2 气囊缓冲动力学模型
排气式气囊缓冲过程以排气口是否开启为界,可视为等熵压缩与排气释能两个阶段。其主要区别是等熵压缩阶段回收载荷的动能完全转化为气囊内气体的内能,而排气释能阶段回收载荷的动能除了转化为气囊内气体的内能之外,还有一部分转化为排出气体的动能和内能。
为便于分析计算,气囊内气体视为压强、温度、密度等气体状态参数均匀分布的理想气体。
新一代载人飞船试验船采用由6个水平圆柱式气囊组成的缓冲气囊系统对返回舱进行缓冲,每个水平圆柱式气囊又由排气式外囊与不排气的内囊组成,其简化模型如图1所示。
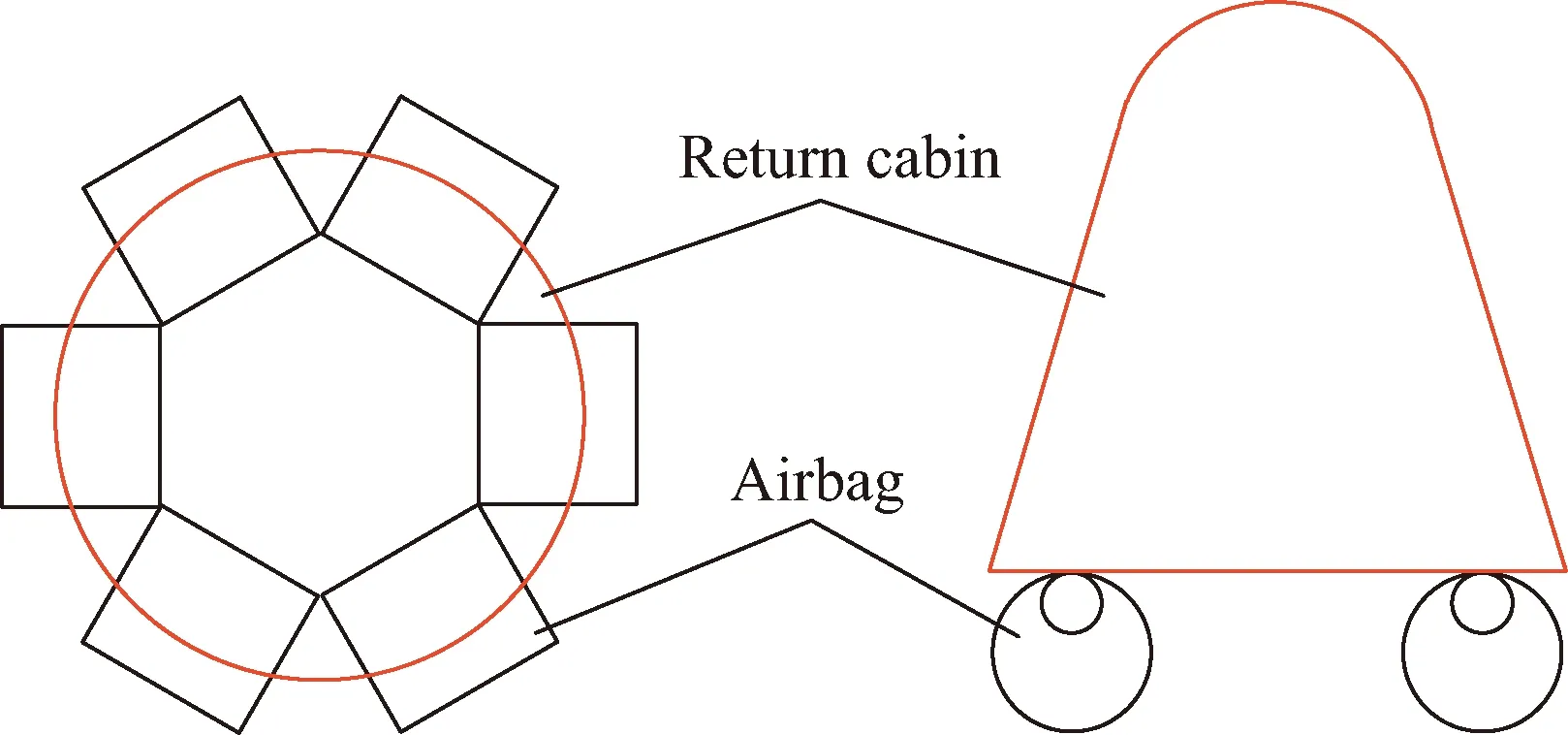
图1 缓冲气囊系统简化模型Fig.1 Simplified model of cushion airbag system
假设返回舱底部为平板且压缩过程中不会内陷到气囊中,同时气囊截面的变形过程为理想的对称变形模式,则单个气囊横截面的变化过程如图2所示。

图 2 缓冲过程气囊横截面变形示意Fig.2 Schematic diagram of airbag cross-sectional deformation during cushioning
由图2可得缓冲过程中单个外囊体积V1、与地面接触面积A1为[13]:
式中:D为外囊直径;H为缓冲过程外囊高度;L为外囊长度。
单个内囊体积V2、与地面接触面积A2(内囊触地时)为:
式中:d为内囊直径;h为缓冲过程内囊高度;l为内囊长度。
2.1 等熵压缩阶段
气囊缓冲过程往往耗时极短,一般不超过0.2 s,因此缓冲过程中气囊内外的热交换极小,可以忽略。气囊未排气阶段其里面气体可视为做等熵压缩,其动力学方程可表示为[14-17]:
式中:m为载荷质量;t为缓冲时间;x为气囊高度;u为返回舱的速度;p1、p2分别为外囊和内囊内压力;p0为环境压强;g为当地重力加速度;γ为气体的绝热系数;下标i表示对应各物理量初始状态值。
2.2 排气释能阶段
排气释能阶段缓冲气囊在继续压缩的同时,气囊里面被压缩的气体通过排气口向外排出,带走大量的能量。这一阶段中,回收载荷的动能首先转化为气囊内气体的内能,然后通过排气过程转化为排出气体的动能,最后排出气体的动能与内能耗散在大气环境中,从而实现缓冲过程中的能量耗散。
气囊排气过程中,排出气体的流速及单位时间排出气体的流量可表示如下:

(1)
式中:K为排气口阻滞系数,取0.7[13];ma为外囊内气体质量;Ae为对应时刻排气口面积;ρe为排气口气体密度;ue为排气口排气速度;qe为排气口单位时间排出气体的质量;Ti为气囊内初始温度;Rm为气体状态常数,单位为J/(kg·K)。
由理想气体状态方程pV=maRmT可得:
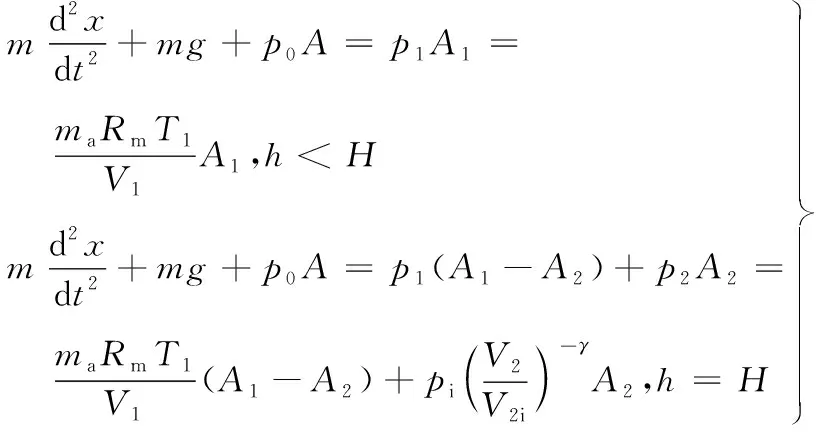
(2)
式中:T1为外囊内气体温度。
(3)
式中:Q1为外囊内气体的内能;i为气体自由度,单原子分子i=3,双原子分子i=5,三原子及多原子分子i=6。
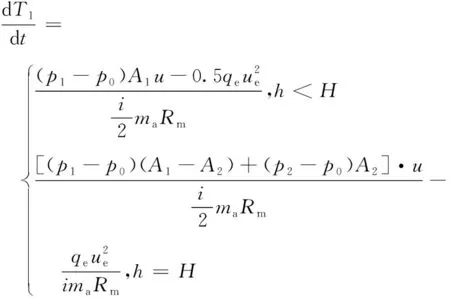
(4)
联立式(1)(2)(4)即为一个三元微分方程组,采用4阶龙哥库塔法求解这一方程组,即可求出排气过程中过载等重要变量,用Matlab软件求解。
2.3 影响缓冲过程的气体参数分析
由前两小节内容可知,影响缓冲过程的气体参数包括气体的绝热系数γ,状态常数Rm以及气体自由度i。
MRm=R
(5)
式中:M为气体摩尔质量;R=8.314J/(mol·K)。 又由分子运动理论,
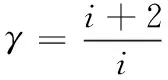
(6)
则在气囊缓冲过程中不同气体介质对缓冲特性的影响可归结为气体自由度i与气体摩尔质量M的不同。
3 仿真分析
3.1 计算模型验证
根据前文建立的气囊缓冲过程动力学模型,本节使用Matlab编写了仿真计算程序,并与相同条件下MSC-Dytran的计算结果进行了比较,如图3所示。其中返回舱质量为7 000 kg;环境大气压力为101 kPa;气囊内填充气体为氮气;外囊直径为1.3 m,长度为1.4 m,单个外囊排气口面积为0.061 m2;单个内囊长度为0.8 m,直径为0.5 m。
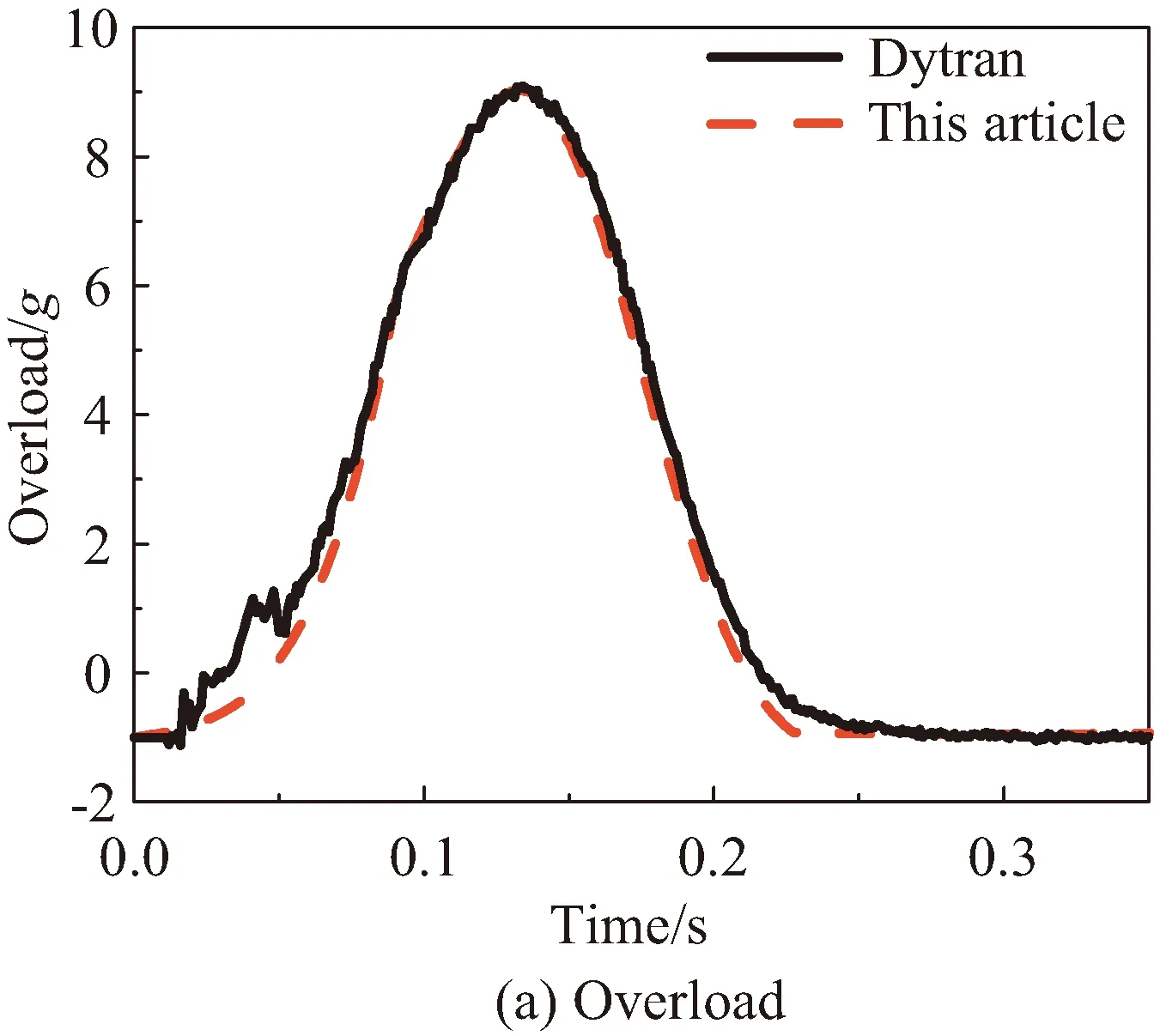
图3 本文模型与有限元模型仿真结果对比Fig.3 Comparison of simulation results between numerical model and finite element model
由图3可以看出,本文模型在缓冲过程返回舱过载与运动速度方面与有限元仿真结果基本一致,仅在返回舱最大反弹速度方面较有限元仿真结果减小了0.7 m/s左右,证明本文的模型有较高的精度。两种计算方法中返回舱反弹速度的差别主要是由于本文模型中忽略了气囊囊体可能出现的褶皱引起的,由囊体褶皱引起的缓冲过载的微小差异在整个缓冲过程中不断累积,最终导致了返回舱反弹速度的差异。
3.2 不同气体介质的缓冲过程
本节对不同气体介质的气囊缓冲过程进行了仿真计算。表1列出了仿真工况的设置情况。

表1 仿真分析工况设置
工况1~7的仿真计算结果对比如图4所示。在等熵压缩阶段,影响气囊缓冲特性的气体介质固有参数只有分子自由度。分子自由度越小,同等压缩程度下气囊内气体压力越大,产生的过载也随之增大。而在排气释能阶段,气囊缓冲特性主要受气体介质的摩尔质量影响。填充不同气体介质时,缓冲气囊内气体初始物质的量相同,但在排气释能阶段,由于排气速度,囊内气体压力等的不同,导致囊内气体物质的量变化速度不同。气体摩尔质量越大,囊内气体的物质的量减小得越慢,气囊内气体压力越大,对应的峰值过载越大。当气体摩尔质量过小时(如氢气、氦气作为缓冲介质时),外囊开始排气后里面压力降低过于迅速,对返回舱的减速效果较差,主要依靠不排气的内囊对返回舱进行着陆缓冲,导致缓冲过载较大且伴随较大的反弹速度。
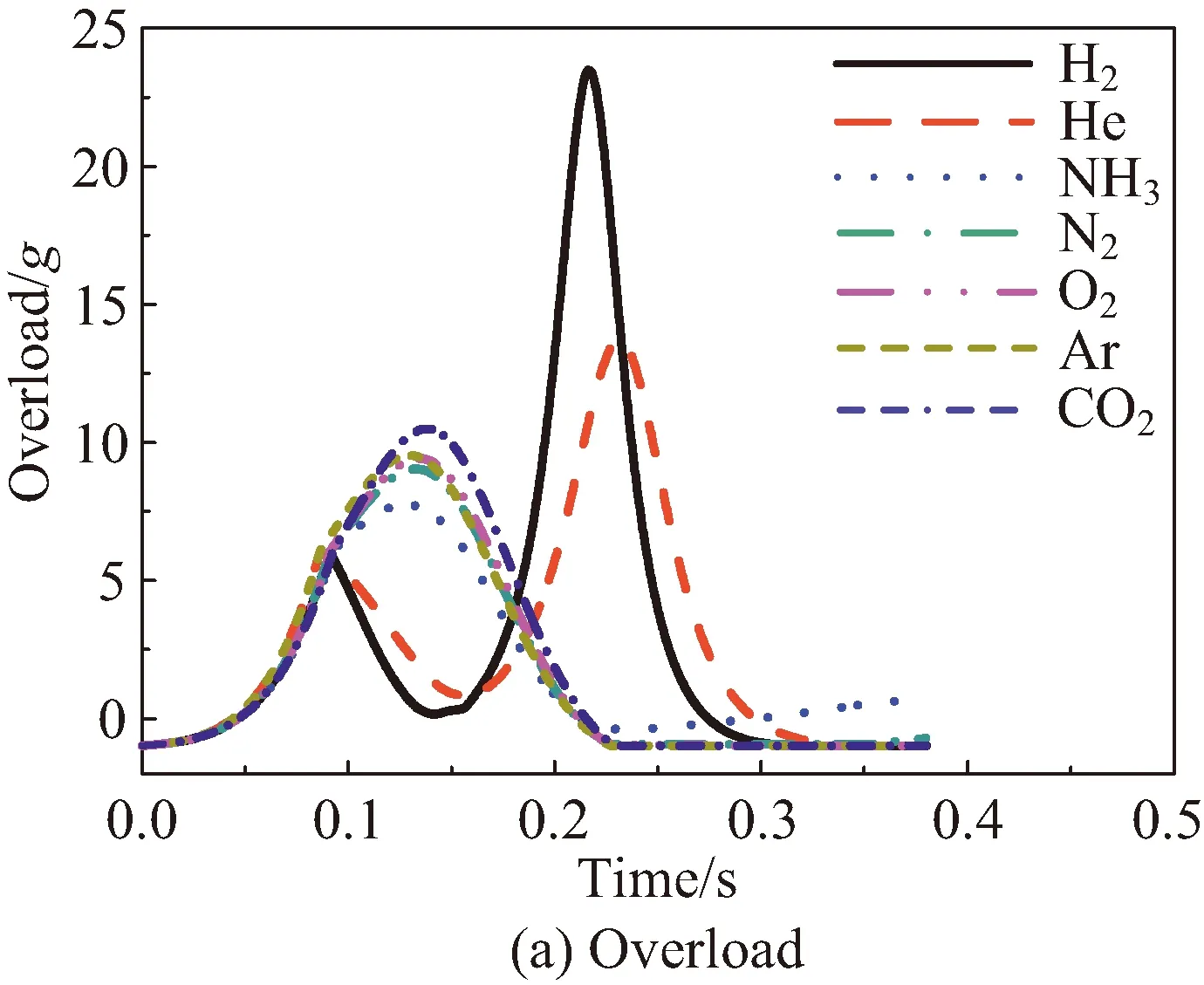
图4 各工况仿真结果对比Fig.4 Comparison of simulation results under different conditions
3.3 针对不同气体介质的气囊排气口面积优化
在气体介质确定的情况下,气囊内气体物质的量的变化速度可通过改变外囊排气口面积加以控制。前文所选择的外囊排气口面积主要适用于以氮气作为缓冲介质的情况,通过调整外囊排气口面积,可以对其他气体作为缓冲介质时的气囊缓冲特性进行优化。对于着陆缓冲过程而言,最重要的两项缓冲特性是峰值缓冲过载与最大反弹速度。氮气作为缓冲介质时返回舱的峰值缓冲过载为9g,最大反弹速度为0.7 m/s,则以峰值缓冲过载≤9g,且最大反弹速度≤0.7 m/s作为优化目标,可得出优化后的缓冲过程仿真结果及外囊排气口面积如图5所示。
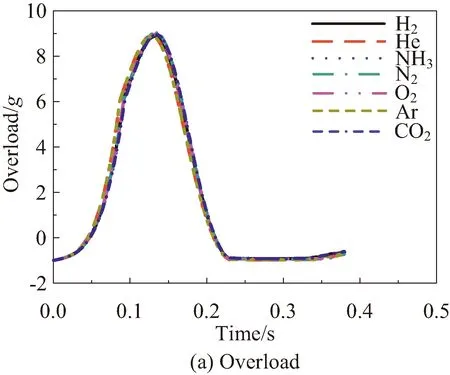
图5 优化后仿真结果及排气口面积Fig.5 Simulation results and vent area after optimization
由图5可知,随着气体介质摩尔质量的增大,为了使得缓冲过程中气囊内气体物质的量保持在一个较为适宜范围内,优化后的外囊排气口面积也随之增大。通过调整外囊排气口面积,使用不同气体作为缓冲介质的缓冲气囊可以达到相近的缓冲效果,缓冲过程中返回舱过载变化曲线及着陆速度变化曲线基本一致,其中峰值过载最大偏差在0.2g以内,峰值反弹速度最大偏差在0.12 m/s以内。
4 结论
本文通过理论推导与仿真分析,可得出如下结论:
1)不同气体介质对气囊缓冲特性的影响主要通过气体的分子自由度和摩尔质量体现,其中等熵压缩阶段气囊的缓冲特性由气体介质的分子自由度决定,分子自由度越小,等熵压缩阶段气囊内压力及缓冲过载增长速度越快;排气释能阶段气囊的缓冲特性受气体分子自由度和摩尔质量的双重影响,气体摩尔质量对气囊缓冲特性的影响更为显著,摩尔质量越大,气囊内气体物质的量下降得越快。缓冲过载越小,但减速效果也随之降低。
2)通过优化气囊排气口面积,采用不同气体介质的缓冲气囊可以达到相近的缓冲效果,气体介质摩尔质量越小,所适用的气囊排气口面积越小。
另一方面,本文仅从理论角度对几种常见气体用作气囊缓冲介质时的缓冲特性进行了研究与分析,并未考虑气体使用过程的安全性、贮存性、经济性等因素(如氢气、氨气的安全性与储存性较差[21-22]),也未考虑排气口面积不同时,加工相对误差控制难度不同等因素。后续工程应用阶段,在缓冲气囊用气体介质选择时,还应结合气体的安全性、贮存性、经济性、对应气囊加工难度等因素进行综合分析。

