3DS Max软件在中学数学立体几何教学中的应用

杜宁贝

[摘  要] 立体几何一直是中学（特别是高中）数学教学的重点内容和难点内容，在中学阶段，学生的空间想象力还未发展成熟，对于理解立体几何存在难度. 文章介绍了三维动画制作软件3DS Max的基本功能与优点，并根据教学实例说明了该应用软件的可行性和必要性.

[关键词] 中学数学;立体几何;3DS Max软件

[⇩] 引言

立体几何是中学数学教学内容，同时也是重点和难点，目的在于从无到有地培养学生的空间想象力，即对客观事物的空间形式（空间几何形体）进行观察、分析、认知的抽象思维能力. 但在实际教学过程中，传统的粉笔作图教学方式很难表达出空间图形的立体感，因而对于空间想象力还处在初级阶段的大部分学生难以理解，影响了他们对立体几何知识的学习和领悟. 随着教育理念、基础设施和师资力量的增长，不少教师已经将国内外针对数学学科教育开发的软件，如几何画板、GeoGebra、超级画板等引入课堂，取得了一定的成果，但在立体几何领域收效有限. 究其原因，是这些软件的主要用途在于平面几何，并没有针对立体几何绘图的优化和设计，特别是没有表现动态视角下的立体几何的功能，但3DS Max软件的出现很好地解决了这一问题. 文章旨在将三维动画制作软件（3DS Max软件）引入中学数学立体几何的教学，配合传统数学教学方式帮助学生更好地进行学习和理解.

[⇩] 3DS Max软件功能简介

3D Studio Max软件，常简称为3D Max软件或3DS Max软件，是Discreet公司开发的（后被Autodesk公司合并）基于PC平台的三维动画渲染和制作软件. 在最新版的3DS Max（2018）中，能够提供三维造型、涉及材质、环境布置、动画制作等功能，上至好莱坞电影特效的制作，下至简单图形的绘制，其已经广泛应用于广告、影视、工业设计、建筑设计、三维动画、多媒体制作、游戏、辅助教学以及工程可视化等领域. 3DS Max软件在中学数学立体几何教学中有以下优点.

1. 3DS Max软件能够完成中学数学立体几何教学内容的设计与实现

中学数学中立体几何教学的目的是培养学生的空间想象力，最终使学生能够达到：

（1）根据空间几何形体或根据表述几何形体的语言、符号，在大脑中展现出相应的空间几何图形，并能正确想象其直观图.

（2）根据直观图在大脑中展现出直观图表现的几何形体及其组成部分的形状、位置关系和数量关系.

（3）对头脑中已有的空间几何形体进行分解、组合，产生新的空间几何形体，并正确分析其位置关系和数量关系.

对应于中学教材，特别是人教版必修2中的第一章“空间几何体”与第二章“点、直线、平面之间的位置关系”，要能够很好地表现出这些空间图形的立体感，同时能够动态展开（三视图、旋转体）. 3DS Max软件的功能可以实现中学数学立体几何教学的全部要求.

2. 3DS Max软件易上手，学习资料丰富，交流方式多

与大部分人对专业动画软件的印象不同，3DS Max软件其实是一款很容易上手的软件. 以笔者自身为例，从软件的下载安装到自学再到完成第一次应用于圆锥曲线的课程设计，仅仅用了一周时间. 3DS Max软件的制作流程非常简洁高效，而中学数学立体几何教学所需要用到的功能其实很少，只要能够针对性地学习，很快就能够学会相关的功能. 在进行几次初步尝试后，就能够完成教学内容的设计. 同时，在学习3DS Max软件方面，不需要有专门学习的人士指导，互联网上有丰富的学习资料，还可以通过百度贴吧、网络论坛等媒介交流制作心得.

3. 3DS Max软件制作流程短，完成效果好

这也是3DS Max软件在进行立体几何教学中比起常规数学教学软件如几何画板等一个不可替代的优势. 學会3DS Max软件一些简单的命令后，完成立体几何教学内容的动画（绘制空间图形→设置关键帧→设置摄像机→完成渲染）仅仅需要几个小时. 同时在绘制空间图形、表现空间动画方面也更胜一筹，3DS Max软件可以通过设置完成透视图的表现，其中还有布尔运算能够制作出切面的图案甚至动画.

[⇩] 3DS Max软件的应用实例——不规则几何体的切面例题讲解

1. 教学内容设计

笔者在中学数学教学过程中，发现学生因空间想象力不足，在理解不规则几何体的切面上存在一定难度，以下即为典型的不规则几何体的切面例题.

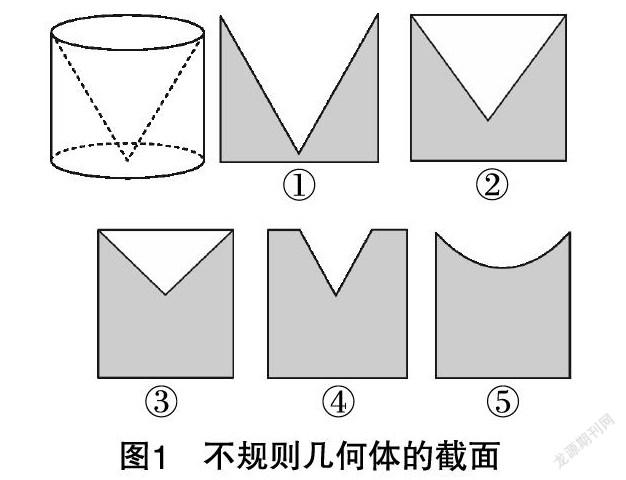
图（图1）中最左边的几何体由一个圆柱挖去一个以圆柱的上底面为底面，下底面圆心为顶点的圆锥而得. 现用一个竖直的平面去截这个几何体，则截面图形可能是（    ）

A. ①② B. ①③

C. ①④ D. ①⑤

该例题的正确答案是D，对于空间想象力强的学生而言，这是一道比较简单的题目. 然而在笔者执教的两个高一班级中，还是有40%左右的学生没能做对. 其中，学生比较容易错误选择的答案是A（约27%）和B（约13%），且这些学生普遍反映，经过笔者的初步讲解也无法很好地理解截面图形为何呈选项⑤的弧形. 该题目讲解的难度大在于使用黑板绘制图形，用平面表达立体效果差;而现实中很难找到这样一个不规则几何体供学生参考，凭空讲解对于这部分学生来说难以理解. 因此笔者决定尝试使用3DS Max软件进行立体动态演示，帮助这些空间想象力不足的学生直观这一不规则几何体实际被切割时的截面图形.

笔者使用的是3DS Max（2014）试用版，目的是多视角展示出这一不规则几何体被竖直平面切割时可能呈现的图形.

第一步是建立模型. 使用“创建—几何体—标准基本体—圆柱体”得到一个圆柱体，再同样使用该功能创建一个底面与之前创建的圆柱体的底面相同、高相等的倒立的圆锥体. 选中创建的圆锥体，使用“创建—复合对象—布尔—差集（B-A）”功能，再选中圆柱体，即可得到例题中的不规则几何体.

第二步是创建竖直平面，并用其截取该不规则几何体. 使用“创建—几何体—标准基本体—平面”绘制一个竖直平面，并让该平面和不规则几何体保持一定距离. 选中平面，使用“设置关键点—拖动时间轴—移动平面—设置关键点”功能，让平面在设定的时间内均匀地切割该不规则几何体.

第三步是多视角下切割动画的输出. 笔者认为一个从斜上方俯视和一个旋转的视角可以完整描述该不规则几何体被切割的情形. 使用“创建—摄像机—自由”绘制一个从右上方俯视的视角，命名为“摄像机1”，再通过“渲染—渲染设置—活动时间段—摄像机1”得到俯视视角下的切割动画. 使用同样的方式创建一个“摄像机2”，视角调整为平视该不规则几何体，再通过“渲染—渲染设置—活动时间段—摄像机2”得到平视视角下的切割动画. 最后选中平面，使用“创建—复合对象—布尔—交集”得到平面截该不规则几何体的图形. 重复上述渲染的步骤，得到俯视视角下的切割动画以及平视视角下的切割动画.

第四步是视频制作. 运用会声会影将4个镜头输出的动画整合到一个画面，并进行简单的文字解释以及后期制作，配合教案完成整个易错题例题的解析课教学内容的设计.

2. 实际教学

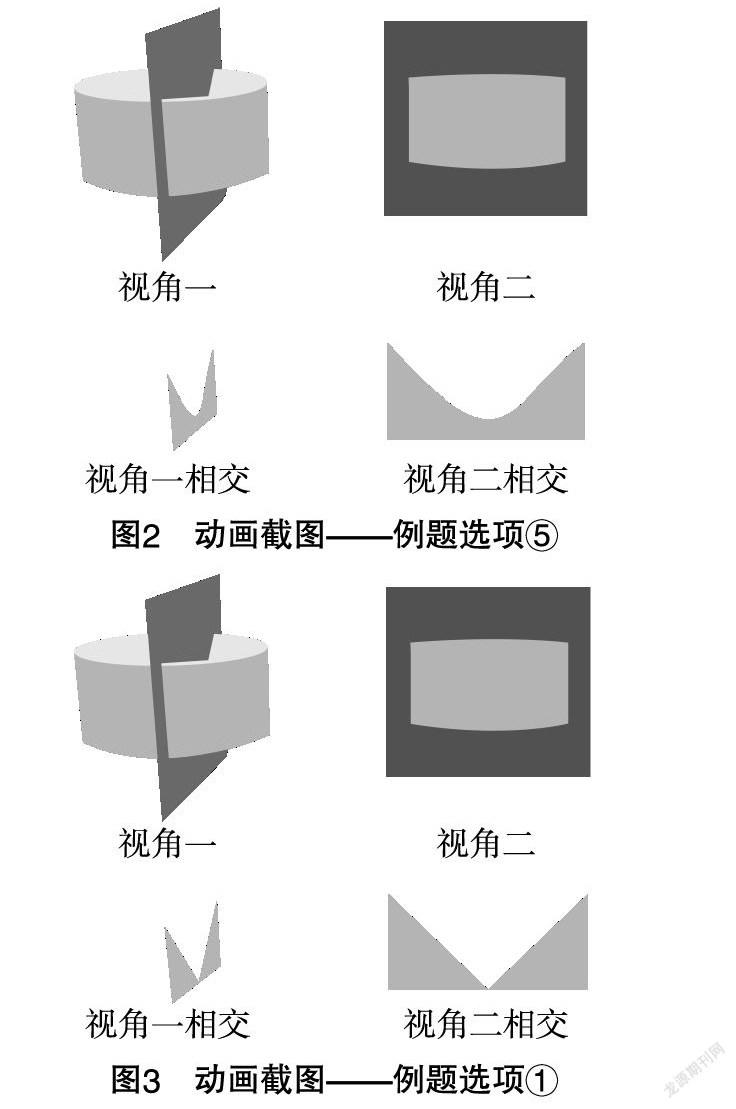
笔者分别在执教的两个高一班级进行了这个例题的讲解课，授课按照“例题错选分析—视频播放讲解—学生交流反馈”的流程进行. 在视频播放讲解中，利用3DS Max软件制作的动画视频，使得学生对于该不规则几何体被竖直平面所截得到的图形有了一个全方位动态的了解，随着竖直平面从该不规则几何体外部接触到切割再到离开，其截面呈现出何种图形，都能直观地在视频中看到. 其中，视角一是俯视视角，视角二是平视视角. 图2和图3展示了动画中的两个瞬间截图，通过截图可以知道答案是D，①和⑤是該不规则几何体被竖直平面切割可能出现的图形.

3. 反馈与效果评价

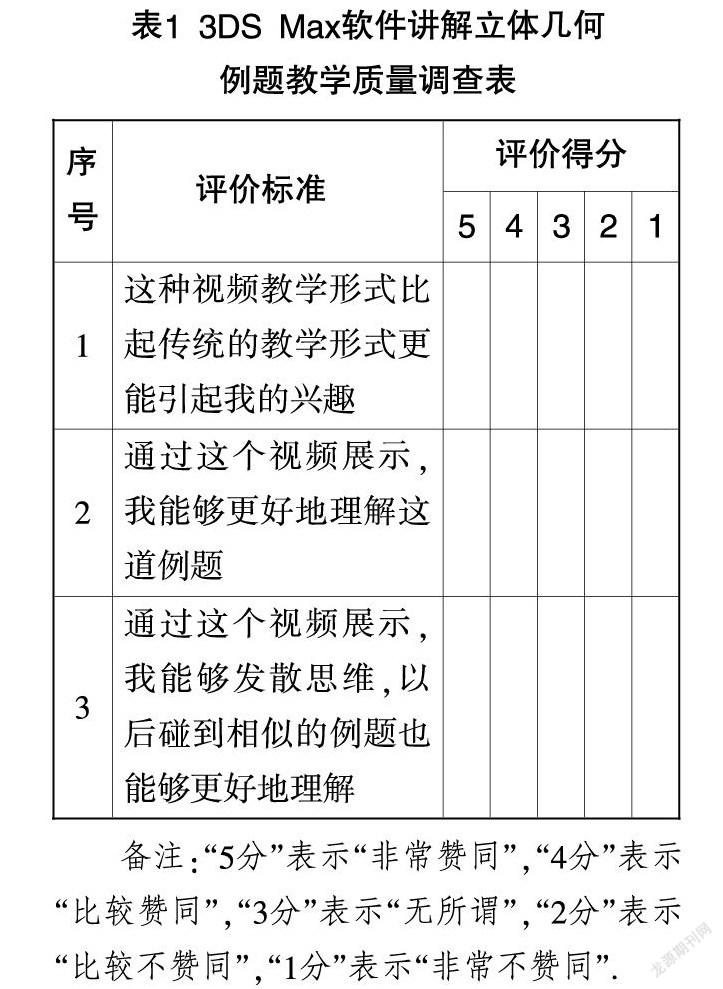
即便学生普遍反映喜欢这类视频教学形式，但是对于将3DS Max软件引入高中数学立体几何教学的效果如何，笔者仍然通过一些简单的问卷做了进一步的了解. 在教学环节的第三部分，笔者发放了一份自己设计的教学问卷（两个班级共计学生87名，回收问卷87份，有效问卷87份）.

备注：“5分”表示“非常赞同”，“4分”表示“比较赞同”，“3分”表示“无所谓”，“2分”表示“比较不赞同”，“1分”表示“非常不赞同”.

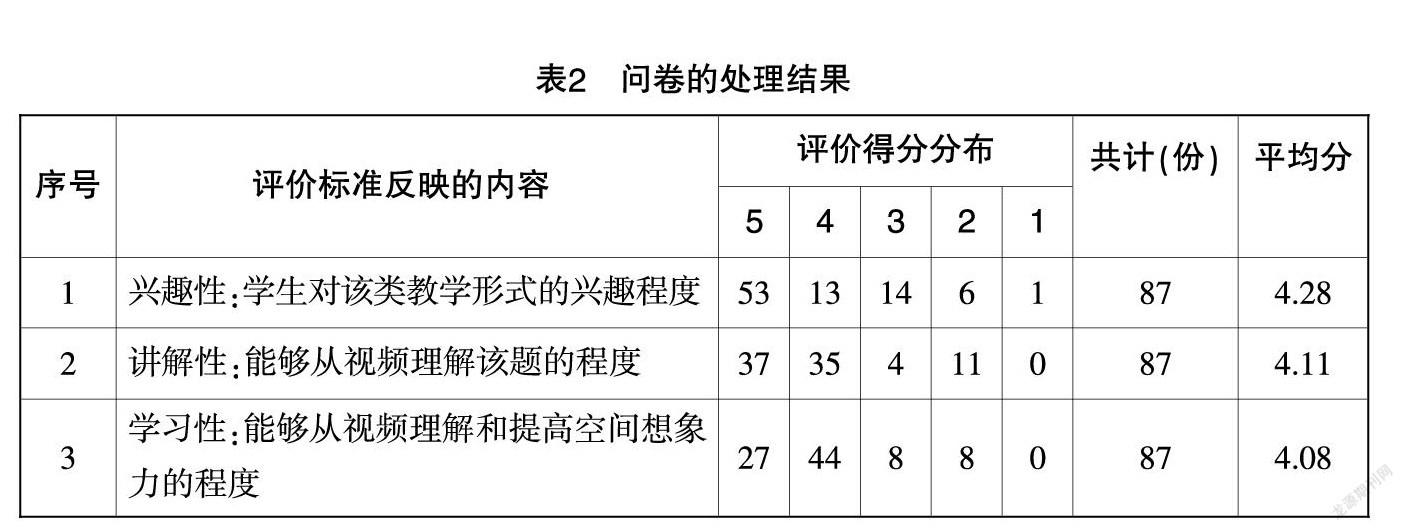
笔者利用Excel对回收的问卷进行了简单的处理，得到的结果如表2所示.

从处理的数据来看，总体上每个序号的平均分都超过了3分，说明此次将3DS Max软件引入高中数学立体几何教学是一次成功的尝试，学生对于该类教学方式产生了较大的兴趣，并且不仅能够更好地理解该例题，对于自身空间想象力的提高也具有帮助. 同时，3个问题的得分基本上相差不大，但还是呈降序排列，分布上“序号1”得到了最多的5分，说明了该类视频教学形式能够很好地引起学生的兴趣，但想要学生完全理解习题、提高空间想象力，难度仍然很大，还需要教师更进一步地努力和尝试.

[⇩] 小结

诚然，3DS Max软件在中学数学立体几何教学中具备一些传统数学教学软件所不具备的优势，同时其功能强大、易于上手、便于操作的可行性和必要性也让我们看到了其应用于中学数学立体几何教学的前景. 3DS Max软件在表现空间几何体、展现动画过程有着其余软件不可替代的优势，其引入中学数学立体几何教学可以帮助学生突破传统教学认知空间的局限性. 但在使用过程中应当注意其作用在于吸引学生的注意力和兴趣、帮助学生理解空间几何体、提高学生的空间想象力，不能让学生过分依赖3DS Max软件而忽视或者疏于自身的思考.