基于序关系-物元可拓模型的澧水幸福度综合评价

乔祺 石林 赵丽子 吴子涵 李代军

摘要：为贯彻落实新时代治水思路，推进湖南省幸福河建设，选取湖南省“四水”之一的澧水为对象，从“防洪保安全”“优质水资源”“宜居水环境”“水生态健康”“先进水文化”“绿色水产业”“文明水管护”7个方面共筛选出21个指标建立了指标体系，基于序关系分析方法和物元可拓理论，构建了体系完整、操作性强、符合实际的序关系-物元可拓模型，对澧水幸福度进行了综合评价。评价结果表明：澧水的综合幸福度属于向优秀转化等級。

关键词：幸福河评价; 评价指标体系; 序关系分析法; 物元可拓模型; 澧水

中图法分类号：X82 文献标志码：A DOI：10.15974/j.cnki.slsdkb.2022.04.020

文章编号：1006 - 0081（2022）04 - 0118 - 05

0 引 言

2019年9 月18 日，习近平总书记在黄河流域生态系统保护和高质量发展座谈会上，第一次提出了“幸福河”概念[1]，为新时代生态文明条件下的黄河流域乃至全国河湖治理与发展提出了新的目标和方向。2020年全国水利工作会议上明确提出要建设造福人民的“幸福河”，必须做到防洪保安全、优质水资源、健康水生态、宜居水环境、先进水文化一个都不能少。幸福河湖是生态保护需求与经济社会发展需求维持平衡的最佳状态，具有动态性、主观性、区域性。幸福河湖要满足人的生态安全需要、经济发展需要、民生福祉需要、文化积淀需要等，进而实现人水和谐共生，这既是幸福河湖深刻内涵的系统表述，也是建设幸福河湖的方向指引。建立科学合理的评价准则与评价方法，致力于打造湖南省幸福河典型示范案例，对新时代水利事业发展意义重大。

澧水位于湖南省西北部，流域跨越湘鄂两省边境，是湖南省“湘资沅澧”四水之一，沿途接纳溇水、渫水、道水和涔水等支流，至津市小渡口注入洞庭湖。干流全长407 km，流域面积16 959 km2，流经张家界、常德两市。澧水流域河网复杂、水能资源丰富、涉河水利工程众多，且上、下游经济社会发展不均衡，沿河各地存在的水问题也不尽相同。自湖南省推行河长制工作以来，澧水流域各地积极开展工作，河流生态环境与群众满意度均明显提升。

本文选取澧水为评价对象，建立了符合湖南省河湖水域特征的评价体系，采用序关系分析方法确定指标权重，基于物元可拓模型完成综合评价。

1 澧水幸福度评价指标体系

幸福河评价[2]是超越传统河湖生态环境评价范畴，具有主观性、地域性以及动态性的研究工作。目前，中国各地对于幸福河内涵的定义不尽相同，相关研究有待进一步深入完善。本文从保持河流的自然结构和满足人类社会合理需求的二元平衡性出发，参考国内现有较为成熟的评价体系和评价指标研究[3-4]，以防洪保安全、优质水资源、宜居水环境、水生态健康、先进水文化、绿色水产业、文明水管护等7个方面建立准则层，并考虑湖南省河流的典型特征与流域经济生态协同发展目标，共筛选出21个指标建立指标层。具体指标如表1所示。

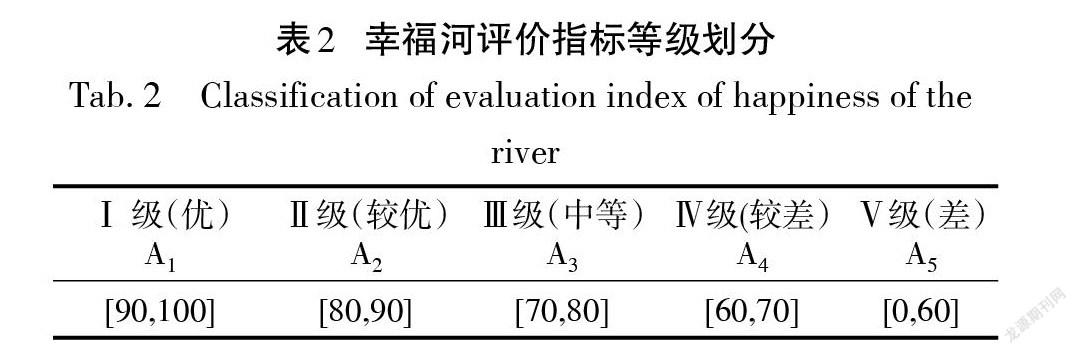
由于原始数据量纲不同，判别标准不一，在进行整体评价之前，对所有指标数据进行等级划分，统一采用百分制评分。本文将幸福河评价标准划分为五个等级，各级评价指标取值范围和含义如表2所示。

2 序关系-物元可拓模型

考虑幸福河评价具有多层次、多指标、定性与定量共存、指标获取的时空复杂性等特点，本文选用序关系法确定评价指标的权重，在此基础上建立物元可拓模型对澧水综合幸福度进行评价。

2.1 指标权重确定

序关系分析法（ G1 法）[5]通过建立指标间的序关系并构造具有一致性的判断矩阵，解决了层次分析法中判断矩阵很难达到一致性的问题。G1法过程简单清晰、操作性强，且无须进行一致性检验，具有较好的实用性。

（1） 根据重要性程度对各级指标进行排序。若评价指标bi相对于评价标准的重要性程度不小于bj，记为bi>bj。如果各评价指标对于评价准则具有关系b1>b2>…>bn，则 b1，b2，…，bn之间按照“>”确定指标间的序关系。

（2） 确定重要性标度。重要性标度即为序关系列表中相邻评价指标bk与bk-1的重要程度之比，记为 hk，且有

[hk=ωk-1ωk]（k=m，m-1，…，3，2）             （1）

式中：[ωk]为第k个指标的指标权重;m为指标的数量;hk∈[1.0，2.0），且 hk 越大，表示指标 bk相对于bk-1越重要。

（3） 计算指标权重。根据各指标间的重要性标度，得出权重的计算公式为

[ωk=1+k=2mi=kmhi-1]                         （2）

[ωk-1=hkωk]                                  （3）

由此可以得出每一指标的权重[ω=ω1，ω2，…，ωm]。

2.2 指标体系评价

物元分析是中国学者蔡文教授于20世纪80年代提出的一种研究物元、解决矛盾或不相容问题的方法，即把研究对象用带有信息的3个要素组成基本元来描述，从而分析研究基本元及其变化规律[6]。本文将物元分析理论应用于幸福河指标体系评价中，不仅能够评价河流“幸福河湖”建设综合水平，还能得到每个单项指标的发展水平，具有明显的科学性和合理性。

2.2.1 物元矩阵构建

将评价对象（描述事物）M、评价对象的指标C及指标数值x结合起来，构成一组描述事物的基本单元，即称为物元。表示为物元R=（M，C，x）。模型应用公式为

[R=R1⋮Rn=C1⋮CnMx1⋮xn]                           （4）

式中：Ci 為待评价对象M的第i个评价指标（i=1，2，…，n）;xi为M关于第i项评价指标对应的量值。

2.2.2 幸福河建设经典域和节域确定

幸福河建设的经典域物元Rj如下所示：

[Rj=Mj，C，Xj=C1⋮CnXj1⋮Xjn=C1⋮Cn（aji，bj1）⋮（ajn，bjn）]       （5）

式中：Mj（ j = 1，2，…，m） 为所划分的第j个幸福河建设评价等级; 区间 Xji = （ aji，bji ） 为Mj 对应指标Ci的取值范围，即经典域。

幸福河建设的节域物元Rp可表示为

[Rp=Mp，C，Xp=C1⋮CnXp1⋮Xpn=C1⋮Cn（api，bp1）⋮（apn，bpn）]       （6）

式中：Mp为评价等级全体;区间 Xpi = （ api，bpi ） 为Mp 关于Ci的取值范围，即节域，[Xji∈Xpi]。

2.2.3 单指标关联函数和关联度确定

关联函数表示待评价物元符合某一等级的程度。令有界实区间X0 =[a，b]的模为| X0 | = | b-a |，则某一点xi到区间x0的距可表示为

[ρxi，X0=xi-12a+b-12b-a]     （7）

由式（7）得到某点xi到经典域区间Xji的距[ρxi，Xji]和到节域区间Xpi的距[ρxi，Xpi]，则幸福河评价M关于等级j的单指标关联度Kj（xi）的计算公式为

[Kjxi=-ρxi，XjiXji， xi∈Xjiρxi，Xjiρxi， Xpi-ρxi， Xji， xi∉Xji]      （8）

式中：[Xji=aji-bji]。若[Kji=maxKj（xi）]，则待评对象第i项指标隶属于评价等级 j。

2.2.4 综合关联度计算与评价等级确定

幸福河建设Mx隶属于某一等级j的程度Kj （Mx）称为综合关联度，表示为

[KjMx=i=1nωiKjxi]                       （9）

式中：[ωi]为各评价指标的权重。若Kjx =max[Kj （Mx）]，则待评对象Mx属于评价等级 j。当 0≤Kj （Mx）<1 时，表示Mx符合标准等级要求;当 -1≤Kj （Mx）<0 时，表示Mx不符合标准等级要求，但具备转化为该标准等级的条件，且数值越大，越容易实现转化;当 Kj （Mx）<-1时，表示Mx不符合该标准等级要求，且不具备转化成标准等级的条件。

3 实例应用

3.1 指标原始分值

通过查阅分析《湖南省澧水干流“一河一策”实施方案（2018-2020年）》《湖南省“一河（湖）一策”（2018-2020年）实施评估》《湖南省水功能区限制纳污红线控制指标核算报告》《湖南省主要河流控制断面最小流量方案报告》《湖南省统计年鉴》《湖南省水资源公报》等资料，实地调研及走访澧水沿线居民，并邀请多位专家对各项指标打分，经统计处理得到澧水各评价指标分值（百分制），具体如表3所示。

3.2 权重确定

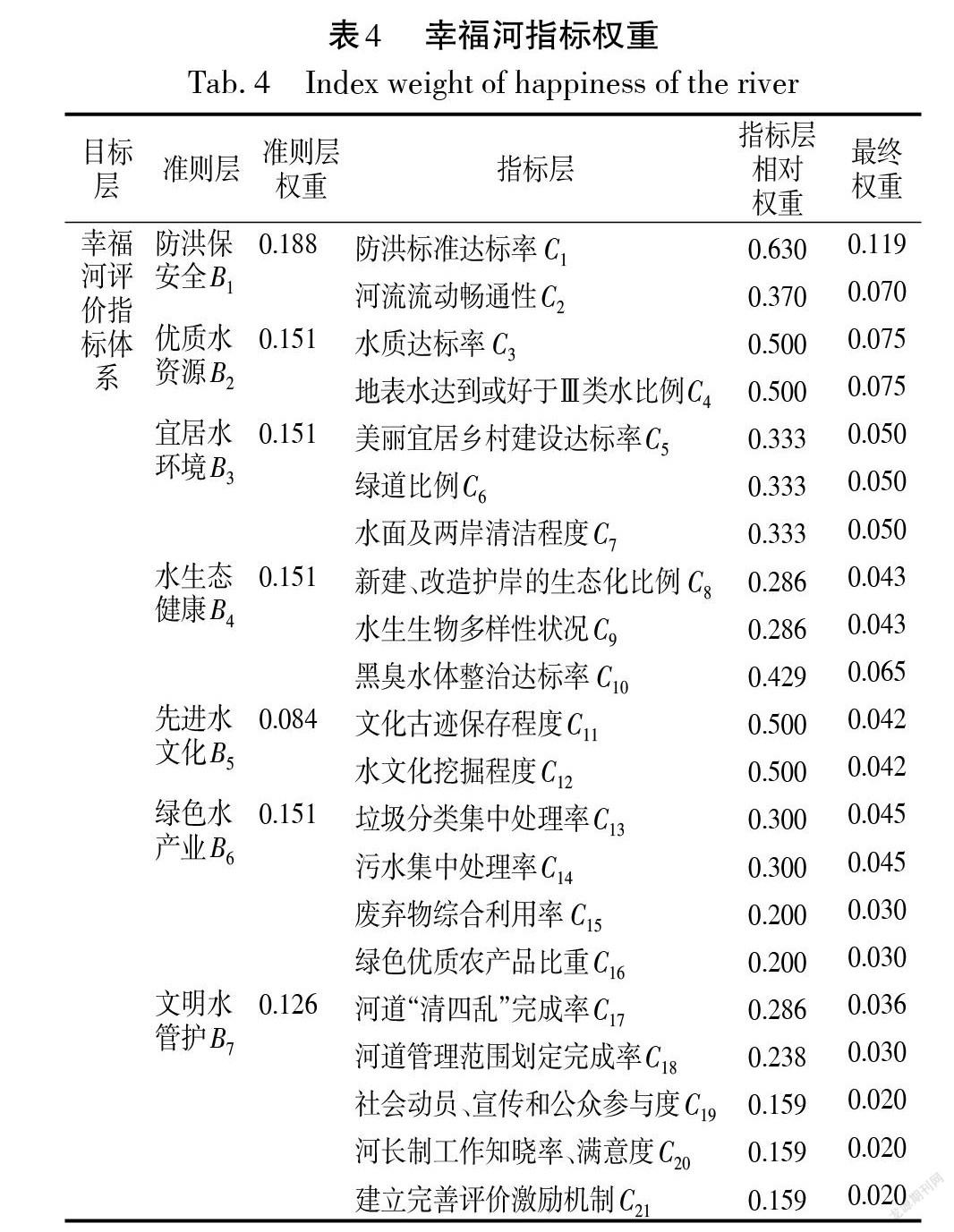
首先确定准则层指标间的序关系，将防洪保安全B1、优质水资源B2、宜居水环境B3、水生态健康B4、先进水文化B5、绿色水产业B6、文明水管护B7准则层指标按重要性从大到小排序为：B1，B2，B3，B4，B6，B7，B5。通过资料查阅、咨询专家确定重要性标度为{1.25，1.00，1.00，1.00，1.20，1.50}。根据式（2）～（3）得到准则层权重如表4所示。

再对每个准则层下的指标层建立序关系。以防洪保安全层为例，包括两个评价指标，对其按照重要性排序，依次为防洪标准达标率C1、河流流动畅通性C2。根据湖南省情与澧水防洪特点， C1指标相对C2指标比较重要，重要性标度C1/C2设为1.7，代入式（2）和式（3），得出防洪保安全指标层的相对权重。各指标最终权重=指标层相对权重×准则层权重。同理确定其他指标的权重，具体计算结果如表4所示。

3.3 综合评价

3.3.1 经典域、节域确定

根据幸福河建设综合评价的可拓性，将澧水幸福河建设的各评价指标发展阶段划分为5个等级，即Ⅰ级（优） 、Ⅱ级（较优）、Ⅲ级（中等）、Ⅳ级（较差）和Ⅴ级（差），确定各等级每项指标的经典域及节域取值，节域取值空间均为[0，100]，如表2所示。

3.3.2 各指标关联度计算

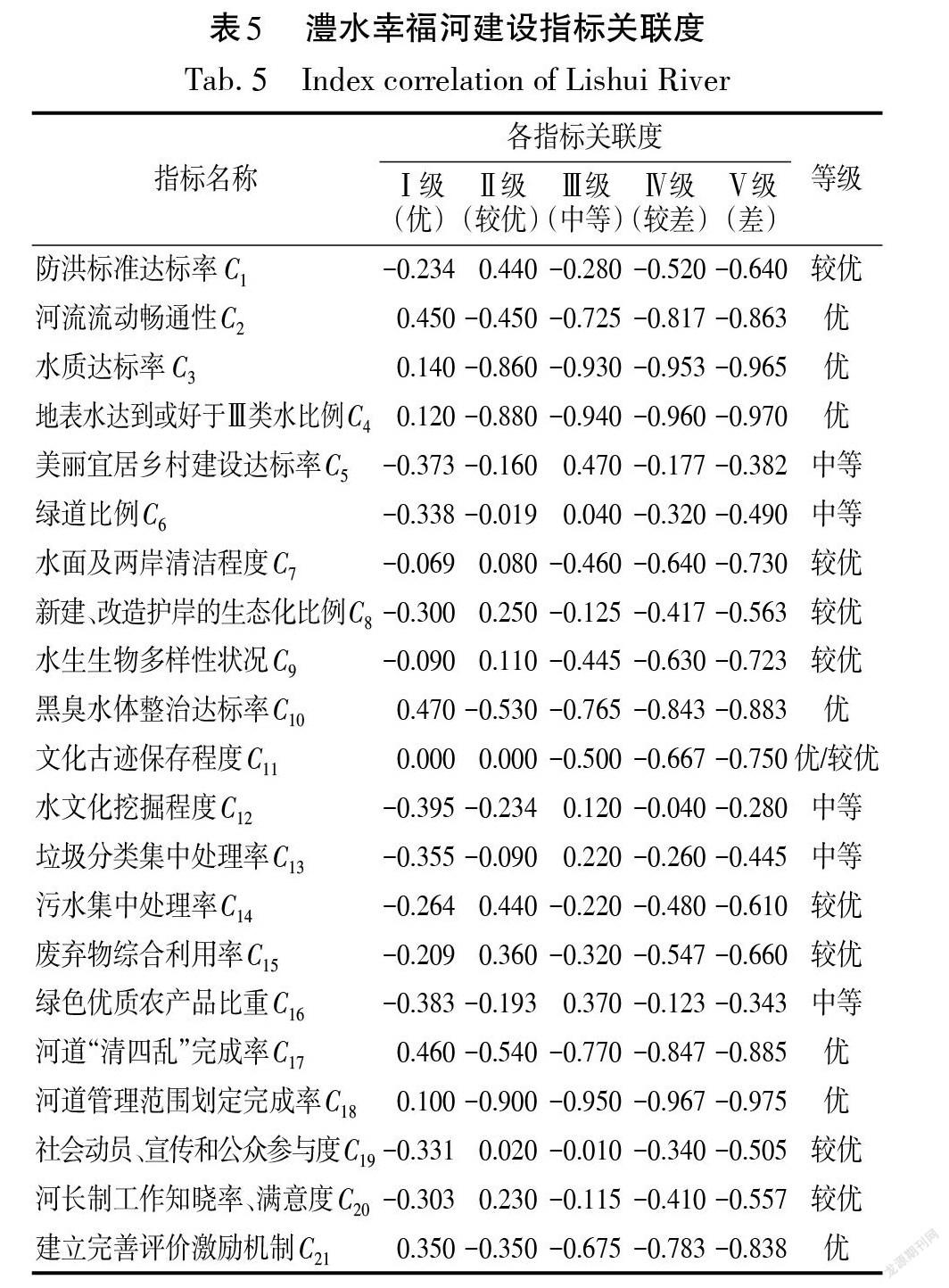
将各指标数据分别代入关联函数公式，得出相应的指标对各等级的关联度。以C1防洪标准达标率指标为例，将x1=85.6代入式（8），可得该指标对应于Ⅰ～Ⅴ级各评价等级的关联度分别为-0.234，0.440，-0.280，-0.520，-0.640，可判定该指标水平属于较优，各幸福河评价指标水平如表5所示。

3.3.3 评价等级

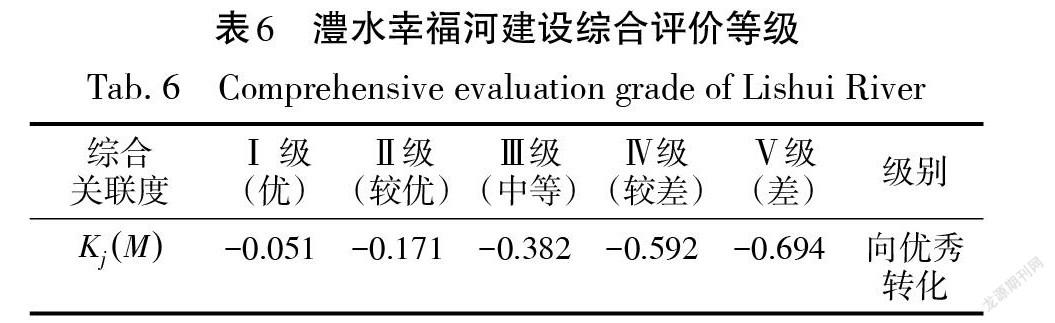
将得到的各项指标对应各等级的关联度与其对应的权重（表5）代入式（9），得出澧水幸福河评价所有指标的综合关联度，如表6所示。

由上表可知[Kjx=maxKj（Mx）=K1（M）=-0.051]，故-1≤Kj（Mx）<0，表明澧水尚不完全符合幸福河建设Ⅰ级的标准，但[-0.051∈[-1，0）]，且非常接近0，说明具备向Ⅰ级转化的条件，即澧水整体幸福度等级为向优转化。

分析表5单个指标的关联度信息，河流流动畅通性、水质达标率、地表水达到或好于Ⅲ类水比例、黑臭水体整治达标率、文化古迹保存程度、河道“清四乱”完成率、河道管理范围划定完成率、建立完善评价激励机制等指标均处于优秀水平，这主要与澧水整体水质较好，河流连通性较好，湖南省河湖管理体制机制日趋完善，大力推动“清四乱”与河道划界工作等因素相关;美丽宜居乡村建设达标率、绿道比例、水文化挖掘程度、垃圾分类集中处理率、绿色优质农产品比重等指标处于中等级别，与优秀水平还有一定距离，这主要与澧水上下游经济发展水平不均衡，自然岸线保有率较高等因素有关。

4 结论与展望

幸福河建设是新时期治水管水的重要任务，本文从防洪保安全、优质水资源、宜居水环境、水生态健康、先进水文化、绿色水产业、文明水管护7个方面优选出21个评价指标构建澧水幸福河评价指标体系，基于层次分析-物元可拓模型，确定各指标权重，并进行各项关联度和总体关联度计算。评价结果显示：澧水整体幸福度虽未完全符合优秀等级但具備向优秀等级转化的条件，与实际情况基本相符，证明了模型的有效性，为湖南省幸福河湖建设提供了参考依据。基于本文结论，建议澧水沿线各市县进一步加强堤防达标建设，大力推动美丽乡村建设，深入挖掘水文明内涵，提升城乡垃圾分类集中处理率，推进绿色农业发展，最大程度提升澧水幸福度。同时，“幸福河”评价指标体系具有一定主观性与地域性，湖南省地貌复杂，水系众多，社会经济发展水平不均衡，本文选取的研究对象澧水在湖南省具有一定代表性，但对于全省各地更具普适性的科学评价体系仍有待进一步研究。

参考文献：

[1] 许玉姣.黄河流域生态环境治理与高质量发展[J].甘肃科技纵横，2020，49（8）：18-20.

[2] 陈茂山，王建平，乔根平.关于“幸福河”内涵及评价指标体系的认识与思考[J].水利发展研究，2020，20（1）：3-5.

[3] 左其亭，郝明辉，姜龙，等.幸福河评价体系及其应用[J].水科学进展，2021，32（1）：45-58.

[4] 韩宇平，夏帆.基于需求层次论的幸福河评价[J].南水北调与水利科技（中英文），2020，18（4）：1-7，38.

[5] 王雪，方国华，李鑫.基于序关系分析-模糊物元法的昆山市节水型社会建设综合评价[J].水利经济，2020，38（5）：30-35，76.

[6] 张俊华，吕学梅，陈南祥，等.基于物元可拓模型的水资源承载力分析[J].人民黄河，2011，33（5）：33-35.

（编辑：李 晗）

Comprehensive evaluation on happiness of Lishui River based on order relation analysis method and matter-element extension model

QIAO Qi， SHI Lin， ZHAO Lizi， WU Zihan， LI Daijun

（Hunan Institute of Water Resource and Hydropower Research， Changsha  410007， China）

Abstract：In order to implement the idea of water control and management in the new era and promote the happy river construction in Hunan Province， this paper selected Lishui River， one of the “Four Rivers” in Hunan Province， as the object， based on 21 indexes about “flood control and safety”， “high quality of water resources”， “livable water environment”， “water ecological health”， “advanced water culture”， “green water industry ” and “civilized water management and protection” and established the evaluation system. Based on the order relation analysis method and matter-element extension theory， a complete， easily operated and practical system was established to comprehensively evaluate the happiness degree of Lishui River. The evaluation results showed that the comprehensive happiness of Lishui River belonged to the level of  “development toward excellent”.

Key words： happy river; evaluation indexes system; order relation analysis method; matter-element extension model; Lishui River