基于指标洪水法的江西省区域性洪水频率分析研究

卢满生 顾盼 陈玺

摘要：为进一步研究资料短缺流域设计洪水推求这一工程水文分析计算领域的难题，探索新的可行方法和途径，收集整理了江西省117个水文测站的年最大洪峰流量序列。基于指标洪水法进行了区域性洪水频率分析，推求了江西省九个水文分区的区域性洪水频率综合增长曲线。结果表明：与单站设计洪水成果相比，指标洪水法计算的区域性洪水频率設计成果总体较好，可作为常规的水文比拟法、地区综合法等方法的重要补充。研究成果可为中国中小流域设计洪水推求提供参考依据。

关键词：区域性洪水频率; 指标洪水法; 水文分区; 江西省

中图法分类号：TV122 文献标志码：A DOI：10.15974/j.cnki.slsdkb.2022.04.002

文章编号：1006 - 0081（2022）04 - 0014 - 07

0 引 言

中国大部分省份于20世纪80年代开始陆续编制或修订了中小流域设计洪水计算手册，受当时的水文资料条件和技术水平限制，以推理公式、单位线等经验方法为主，依据设计暴雨间接推求设计洪水。随着中小流域实测洪水资料的进一步积累，可采用设计依据站的实测洪水资料直接推求设计洪水，并采用水文比拟法、地区综合法等途径移用至设计断面。但是，当设计断面难以选择设计依据站或设计依据站的资料条件不符合规范要求时，区域性洪水频率分析方法（Regional Flood Frequency Analysis）能够综合利用区域内多个站点实测资料进行频率分析，从而减少单站估计的任意性，有效提高缺资料地区的设计洪水成果的计算精度，为设计洪水计算提供了新思路、新方法。

区域性洪水频率分析方法首先在欧美等国引起重视，并很快在国内外得到广泛应用。英国于1975年将该方法列入了国家的洪水研究报告《Flood Study Report》[1]，1999 和2007 年的《Flood Estimation Handbook》[2]也提出要开展洪水频率区域分析。美国于1981 年发布的《Guidelines for Determining Flood Flow Frequency （Bulletin 17B）》[3]推荐洪水频率分布曲线的偏态系数值要采用单站和区域偏态系数进行加权计算。熊立华等[4]总结了国际上区域性洪水频率分析方法的研究进展，并对区域性洪水频率分析的经典方法——指标洪水法应该注意的几个关键问题展开了论述。杨涛等[5]基于线性矩法将珠江三角洲区域按照洪水形成动力机制不同而划分成3个水文分区，分别采用各自最佳的分布函数对珠三角地区洪水设计成果进行频率分析。林小丽[6]应用线性矩法和多种回归方法，对淮河息县以上流域进行区域性洪水频率分析。

本文针对江西全省现有九大水文分区，考虑到水文站点的空间分布及资料条件，选取了117个控制流域面积小于3 000 km2的水文站，采用指标洪水法进行区域性洪水频率分析研究，并与单站设计洪水计算成果进行比较，研究其在江西省中小河流设计洪水推求中的适用性。

1 数据与方法

1.1 区域概况及数据来源

江西省地处南岭以北、长江以南，属亚热带湿润季风气候。四季分明且天气复杂多变，具有春寒、夏热、秋燥、冬冷、无霜期长和冰冻期短等特点。根据2010年版《江西省暴雨洪水查算手册》中的自然地理、地貌地形、河流水系以及水文站网、大型水利工程分布情况，将江西省划分为九大水文分区。本次收集整理了江西省抚河、饶河、修水、湖区、赣江、东江及信江等流域共117个中小流域水文站建站以来至2020年的年最大洪峰流量序列，对洪水资料进行了可靠性、代表性、一致性分析，并依据上下游、邻近站点资料，对部分有缺测资料的站点进行了插补延长。水文分区和站点空间分布见图1，各站点集水面积和采用的资料系列长度等基本情况见表1。

1.2 研究方法

1.2.1 指标洪水法步骤

指标洪水法[7]进行区域性洪水频率分析，主要分为3个步骤。

（1） 根据流域特征将具有相似下垫面、水文气象和暴雨洪水等特点的水文站点归为“同一水文分区”，各分区内所有站点要通过三性检验，即不和谐性、异质性和独立性检验[7-8]。本文基于江西省已有的9个水文分区，开展三性检验，通过检验则维持原有分区不变，若不通过检验则采用模糊聚类法[9]进行水文分区划分调整。

（2） 综合各分区水文站点的样本资料，计算各站点线性矩相关参数，确定区域无因次化的洪水频率曲线，也称区域综合增长曲线，主要包括无因次系列生成、单站参数估计、区域参数估计和区域频率曲线推求。

（3） 根据综合增长曲线，查不同频率的增长因子，根据水文站年最大洪峰流量均值推求各个站点不同频率的设计洪水。计算方法如下。

无因次系列生成。将每个水文站点的洪峰系列无因次化：

[qij=QijQi]（i=1，…，N; j=1，…，ni）（1）

式中：N为水文站个数;Qij为第i个水文站第j年最大洪峰流量，m3/s;[Qi]为第i个水文站年最大洪峰流量均值，m3/s;ni为第i个站点年最大洪峰流量的资料系列长度，a。

单站参数确定。根据SL 44-2006《水利水电工程设计洪水计算规范》[10]中的规定，对每个站点，采用P-Ⅲ型频率曲线通过适线法分别确定其无因次q系列的统计参数，参数值记为[θ（i）k]。

区域参数拟定。将区域内所有站点的参数值加权平均，得到区域参数值：

[θRk=i=1Nniθ（i）ki=1Nni]                （2）

区域频率曲线推求。将区域参数值[θRk]代入区域频率曲线q （p），得到区域频率曲线如下：

[q（p）=qpθR1，…，θRs]       （3）

利用区域综合增长曲线推求各个站点不同频率的设计洪水。对任一站点，超过概率p 的设计洪峰流量为

[Qi（p）=Qi·q（p）]                               （4）

1.2.2 三性检验

（1） 异质性检验。采用H值检验方法进行区域异质性检验，设均质区内有N个站点，第i个站点的样本长度为ni，线性矩系数为[t（i）]、[t（i）3]和[t（i）4]，则以样本长度为权重的区域平均线性矩系数为

[tR=i=1Nnit（i）/i=1NnitR3=i=1Nnit（i）3/i=1NnitR4=i=1Nnit（i）4/i=1Nni]                             （5）

式中：[tR]，[tR3]和[tR4]分别为区域平均线性离差系数、偏态系数和峰度系数。

以样本长度为权重的样本线性矩系数L-Cv的均方差公式为

[V1=i=1Nnit（i）-tR2/i=1Nni12]             （6）

选用P-Ⅲ分布，使用区域平均线性矩系数拟合频率曲线，并使用蒙特卡洛模拟进行不少于500次模拟计算，获得V1的均值[μV1]与均方差[σV1]。则异质性度量H值为

[H1=V1-μV1σV1]                           （7）

0≤H1<1表示区域为可以接受的一致区，1≤H1≤2表示可能的异质区，H1>2表示异质区，H1<0表示站点可能存在相关性。除V1外，可采用基于L-Cv和L-Cs的度量H2和基于L-Cs和L-Ck的度量H3作为异质性度量。

[V2=i=1Nnit（i）-tR2+t（i）3-tR421/2/i=1NniH2=V2-μV2σV2]   （8）

在实际应用中，H1的度量强度要高于H2和H3，因而推荐使用H1作为异质性度量标准。

（2） 独立性检验。通过L-Cv检验的一致区，H1<0表明站点间存在不同程度上的相关性，特别是H1<-2表明站点间存在大量的相关性。需要通过去相关来保证站点间的时间和空间独立性。具体步骤如下：① 舍弃资料序列小于20 a的站点;② 计算Pearson相关系数r，当|r|>0.7时，认为站点间存在相关性;③ 在第二步存在强相关性的基础上，进一步通过对100 a一遇洪峰流量估计值的灵敏性检验，来判断站点是否舍弃或保留，采用相对误差RE来评估。

[r=N∑xiyi-∑xi∑yiN∑x2i-（∑xi）2N∑y2i-（∑yi）2] （9）

式中：xi，yi分别为不同站点的资料值。

[RE=q1-q0q0]                     （10）

式中：q0为未去掉相关站点时，一致区的区域增长因子;q1为去掉相关站点时，一致区的区域增长因子。当RE>5%时，认为站点的相关性对整个一致区的洪水频率估计值影响较大，去掉该组站点中序列较短的那个站点资料。

（3） 不和谐检验。初步分区划定后，采用不和谐性检驗指标Di检查区域中是否存在与整个区域不和谐的站点。令[ui=t（i）， t（i）3， t（i）4T]，站点i的不和谐检验指标为

[Di=13（ui-u）TA-1（ui-u）]              （11）

[A=i=1N（ui-u）（ui-u）T]               （12）

式中：[u]为区域线性矩系数的算术平均值，[u=N-1i=1Nui]。

当不和谐度Di低于临界值时，认为区内无奇异点，临界值与区域内站点个数相关，见表2。超过临界Di值的站点，应考虑将其移至另外的区域。

2 结果与分析

2.1 三性检验

（1） 异质性检验。采用H 值检验法来开展水文分区均匀性检验，使用线性矩变差系数t2作为反映频率分布曲线特征的指标θ，针对θ开展检验。以P-Ⅲ分布作为区域频率曲线线型，对9个水文分区，分别重复随机模拟500次。

对每一水文分区的每一次随机模拟，分别计算该分区内线性矩变差系数系列的离散程度，计算各分区的非均匀性指标H，成果如表3所示。各水文分区的非均匀性指标H 值均小于1，故检验分析表明，该9个水文分区都是均匀的。

（2） 独立性检验。根据计算结果，分区Ⅰ～Ⅸ测度H1分别为0.26，0.18，0.09，0.13，-0.08，0.03，

-0.05，0.11和0.52，H1均大于-2，表明站点间不存在大量的相关性，满足独立性检验。

（3） 不和谐检验。对每一分组的每一个水文站点，分别计算其不一致性指标值Di，再与临界值比较，开展不和谐检验。分区Ⅰ～Ⅸ各站点Di范围分别为0.082～1.836，0.260～1.964，0.014～1.952，0.200～1.898，0.122～1.804，0.114～1.798，0.134～1.860，0.054～1.972，0.084～1.280，均满足表2的要求，即各组数据未发现离群点。

综上，江西省9个水文分区满足异质性检验、独立性检验、不和谐检验。因此，本次仍以2010年版《江西省暴雨洪水查算手册》划分的九大水文分区为基础开展研究。

2.2 区域参数估计及频率设计成果推求

对任一水文分区，将分区内站点的样本资料长度作为权重，区域变差系数和偏态系数可由该分区内所有站点目估适线法配线的变差系数、偏态系数分别加权平均计算得到。江西省9个水文分区的区域参数计算成果见表4。

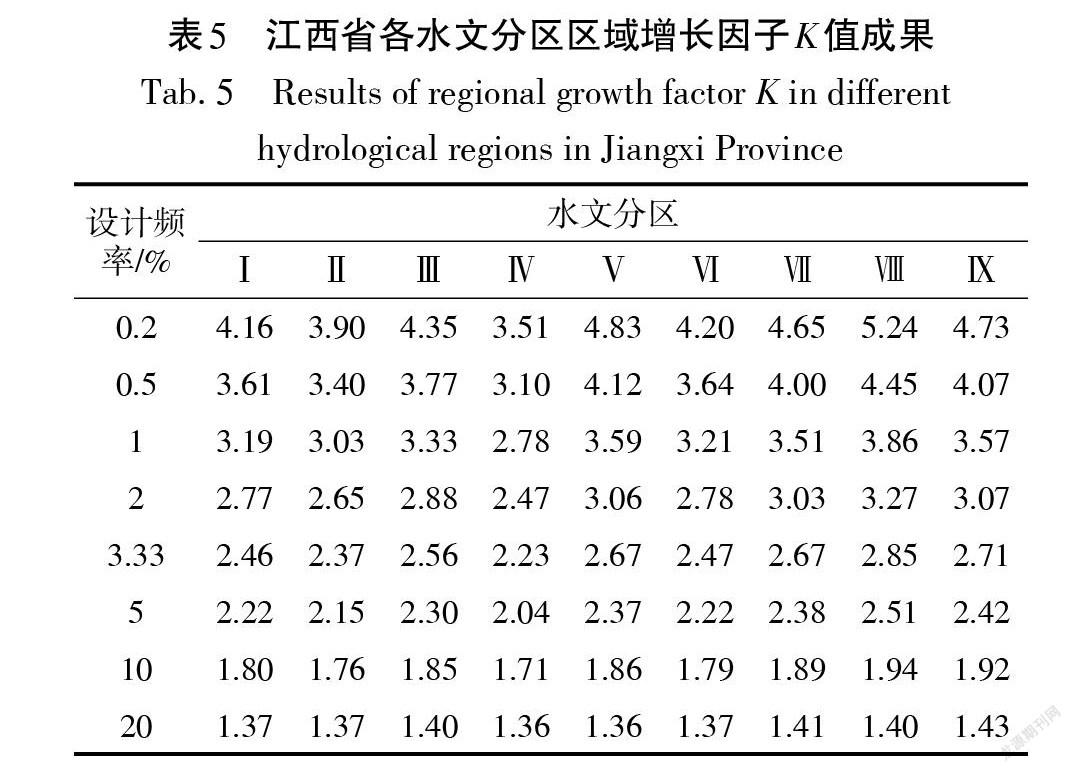
由各区域综合特征参数，可以计算得P-Ⅲ型分布参数[μR]，[δR]，[CRs]的区域估计值，确定区域频率曲线[q（p）=qPμR， δR， CRs]。江西省各水文分区增长因子K成果见表5，基于P-Ⅲ型频率分布曲线的区域增长曲线见图2。

2.3 设计成果合理性分析

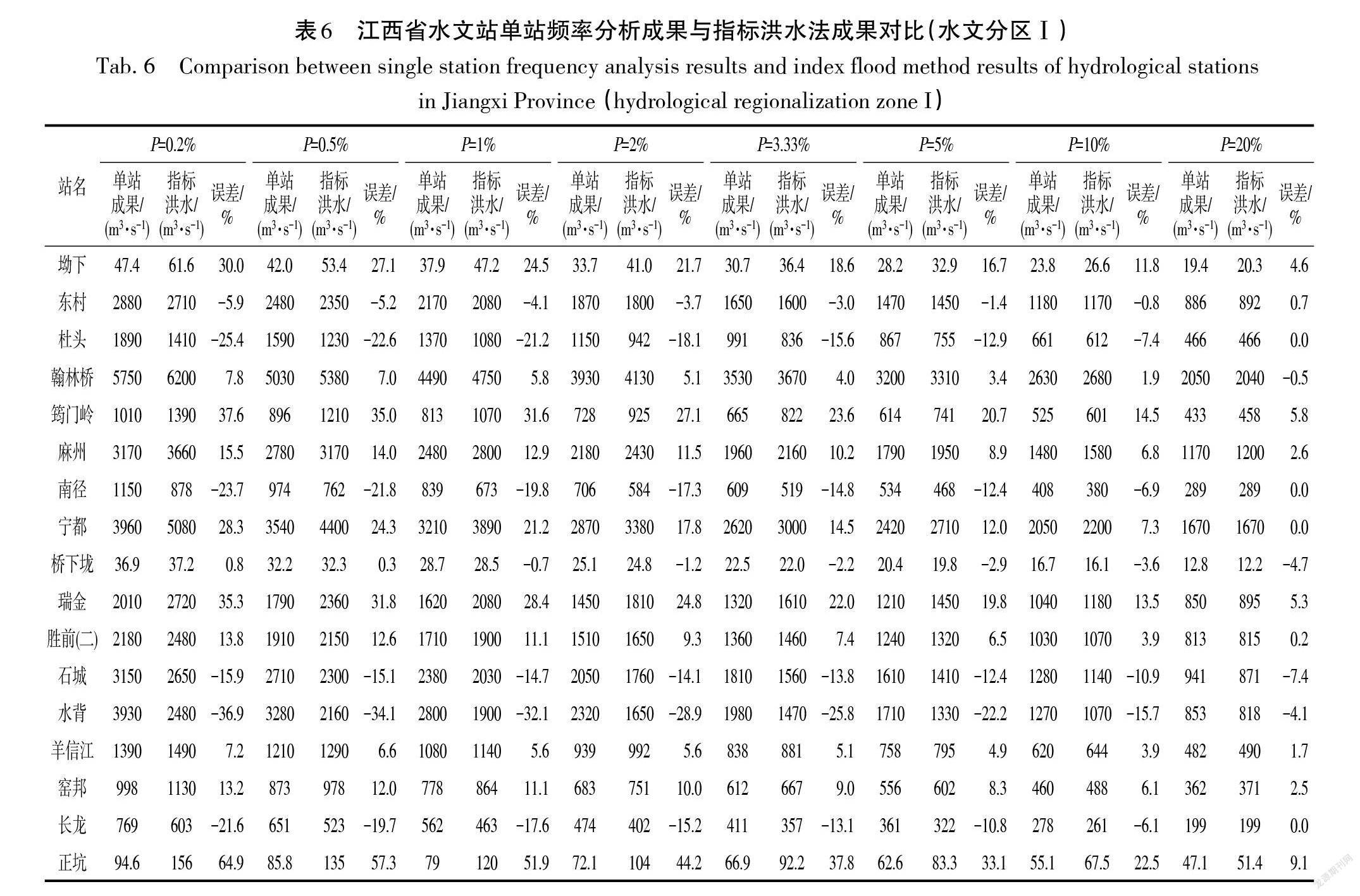
基于指标洪水法的各分区内某水文站不同频率设计洪水成果，可采用不同设计频率条件下该水文站所属水文分区增长因子乘以水文站年最大洪峰流量均值求得。以水文分区Ⅰ（P=0.20%～2%）为例，根据增长曲线推求得出区域性洪水频率设计成果，并将其与单站实测资料进行频率分析结果进行比较。参考GB/T 22482-2008《水文情报预报规范》的相关要求，设计洪水成果相差不超过20%为合格，见表6。统计分区各频率合格水文站的数量与分区水文站总数量比值即为合格率，经分析，水文分区Ⅰ中指标洪水法计算得出设计洪水成果在设计频率低于50 a一遇时，合格率高于70%，100 a一遇以上稀遇频率设计成果合格率较低。

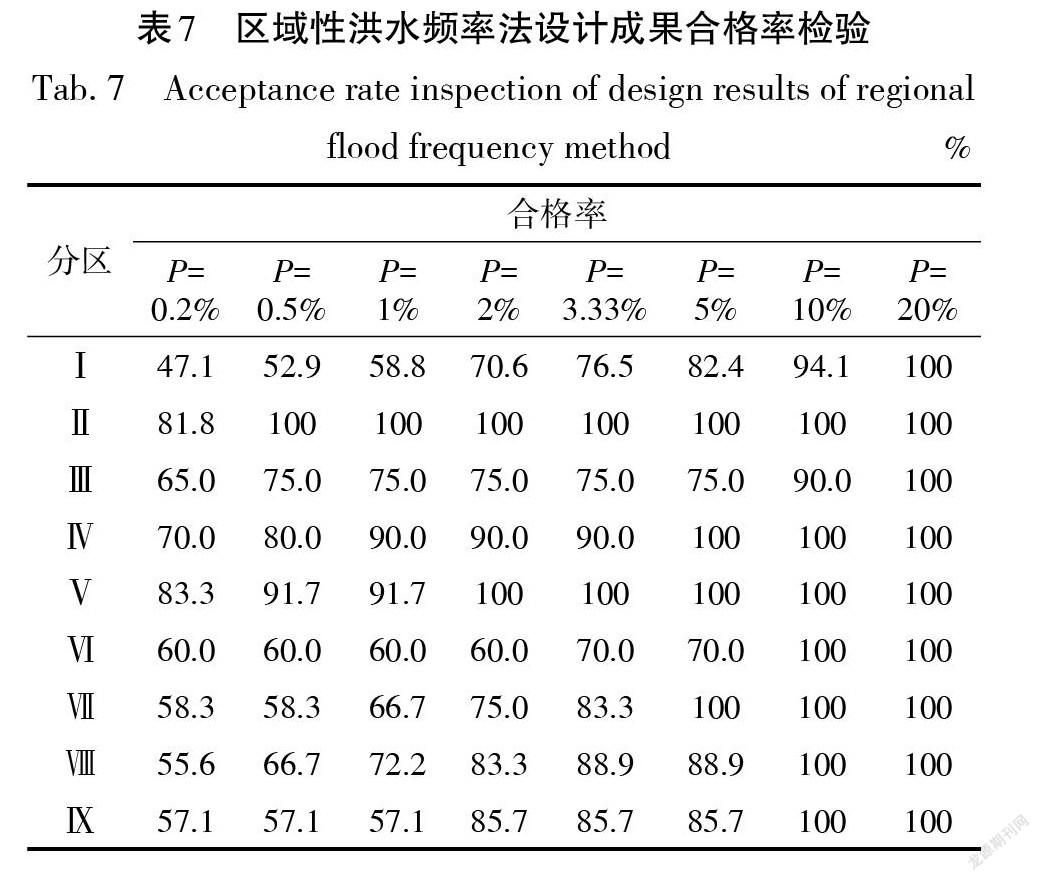
各水文分区采用指标洪水法分析得到的设计洪水成果合格率检验结果见表7。可以看出，水文分区Ⅱ区和Ⅴ区的5 a一遇至500 a一遇重现期条件下基于指标洪水法的区域性洪水频率设计成果合格率达到80%以上，说明该方法在江西省水文分区Ⅱ区和Ⅴ区的适用性较好，采用该方法计算得到的设计洪水成果可作为工程水文设计的重要依据。该方法在水文Ⅳ区表现次之，200 a一遇重现期以下条件下基于指标洪水法的区域性洪水频率设计成果合格率达到80%以上，500 a一遇重现期条件下合格率为70%，采用该方法计算得到设计洪水成果可供参考。水文分区Ⅰ，Ⅲ，Ⅵ，Ⅶ，Ⅷ区和Ⅸ区，对重现期为5 a一遇至50 a一遇条件下基于指标洪水法的区域性洪水频率设计成果合格率达到70%以上，可作为工程水文设计的重要参考依据，但对50 a一遇以上重现期设计洪水成果，需要采取其他方法或途径计算，综合考虑后合理采用。

3 结论与展望

（1） 基于指标洪水的区域性洪水频率分析方法能够综合利用研究区域内多个站点的洪水信息，可作为资料缺乏地区洪水频率计算方法的重要补充。

（2） 对江西省9个水文分区而言，重现期30 a一遇以下的区域性洪水计算结果与单站频率分析结果相差不大，可作为防洪标准较低的工程规划设计的洪水简易估算方法，也可为中小流域应急抢险救灾提供快速决策支撑。

（3） 本文仍存在诸多不足，比如分区的唯一性问题，计算区域增长曲线时使用资料长度作为权重是否最优，以及不同资料长度的典型站点、效果有何区别等，均有待进一步研究。

参考文献：

[1] Natural Environment Research Council. Flood studies report[R]. London：Department of the Environment， 1975.

[2] ROBSON A， REED D. Flood estimation handbook[M]. Wallingford： Institute of Hydrology， 1999.

[3] ENGLAND J J F， COHN T A， FABER B A， et al. Guidelines for determining flood flow frequency—Bulletin 17C[R]. Reston： US Geological Survey， 2019.

[4] 熊立華， 郭生练， 王才君. 国外区域洪水频率分析方法研究进展[J]. 水科学进展， 2004， 15（2）： 261-267.

[5] 杨涛，陈喜，杨红卫，等. 基于线性矩法的珠江三角洲区域洪水频率分析[J]. 河海大学学报（自然科学版），2009，37（6）：615-619.

[6] 林小丽. 区域洪水频率分析在淮河流域的应用研究[D]. 南京：河海大学，2005.

[7] PANDEY G R， NGUYEN V T V. A comparative study of regression based methods in regional flood frequency analysis[J]. Journal of Hydrology， 1999， 225（1-2）： 92-101.

[8] MOSAFFAIE J. Comparison of Two Methods of Regional Flood Frequency Analysis by Using L-moments[J]. Water Resources， 2015， 42： 313-321.

[9] 熊立华， 郭生练. L-矩在区域洪水频率分析中的应用[J]. 水力发电， 2003， 29（3）： 6-8.

[10] SL 44-2006 水利水電工程设计洪水计算规范[S].

（编辑：唐湘茜）

Analysis of regional flood frequency in Jiangxi Province based on index flood method

LU Mansheng1， GU Pan2， CHEN Xi1

（1. Bureau of Hydrology， Changjiang Water Resources Commission， Wuhan 430010， China; 2. Hanjiang Bureau of Hydrology and Water Resources ， Bureau of Hydrology，Changjiang Water Resources Commission， Xiangyang 441000， China）

Abstract： The design flood analysis and calculation for the river basin with insufficient data is still an unsolved puzzle in the field of engineering hydrology. For exploring new feasible methods to improve the deficiencies of the current methods， this paper attempt to analyze the regional flood frequency based on the index flood method by using the maximum peak discharge sequence of 117 hydrological stations in Jiangxi provinces. The comprehensive growth curves of the regional flood frequency of 9 hydrological sub-regions in Jiangxi Province are derived. The results show that compared with the design flood results of a single station by using traditional method， the design results of the regional flood frequency calculated by the index flood method generally have good applicability. It can be used as an important supplement to the conventional hydrological analogy method and the regional comprehensive method. The research provides new methods and important reference basis for the design flood inference in small and medium-sized river basins.

Key words： regional flood frequency; index flood method; hydrological regionalization zones; Jiangxi Province