线性二阶锥权互补问题的非单调无导数下降算法
迟晓妮, 崔然然, 张所滨, 朱 宁
(桂林电子科技大学 a. 数学与计算科学学院/广西自动检测技术与仪器重点实验室/广西密码学与信息安全重点实验室; b. 科学技术发展研究院;c. 信息科技学院, 广西 桂林 541004)
0 引言
线性二阶锥权互补问题(LSOCWCP)是指找到向量x∈Rn使得

(1)
其中连续可微函数F(x):Rn→Rn,K={x=(x1;x2)∈R×Rn-1:x1≥‖x2‖}为n维二阶锥(SOC), 矩阵P∈Rn×n, 向量q∈Rn,w∈K为给定权向量。
线性二阶锥互补问题(LSOCCP)是w=0时的LSOCWCP(1):

权互补问题(WCP)在工程设计、经济及鲁棒优化等诸多领域有着广泛应用[1-2], 是一类重要的优化问题[3], 因此WCP[4-5]的算法研究引起广泛关注。
1 预备知识
目前, 学者们常将互补问题(CP)[6-7]基于效益函数[8-9]转化为极小化问题,运用无导数下降算法[10-11]求解。 这类方法减少了计算工作量, 因为无须计算F的导数。 如GU等[12]利用无导数下降算法求解非线性CP, 讨论算法的全局收敛性及收敛率。 CHEN等[13]分析SOC互补问题(SOCCP), 对SOCCP进行极小化变形求解。
本文推广CP的非单调无导数下降算法求解LSOCWCP,提出新的SOC权互补函数,构造其效益函数, 利用该函数将LSOCWCP转化为无约束极小化问题, 分析其水平集有界性。 为提高算法性能, 算法采用非单调线搜索计算步长, 且是全局收敛的。最后给出非单调无导数下降算法在不同条件下分别求解LSOCWCP和LSOCCP的数值结果。
下面给出一些相关定义。对任意x=(x1;x2),y=(y1;y2)∈R×Rn-1,x和y与SOC相伴的约当积[14]定义为x°y=(xTy;x1y2+y1x2)。x+和x-分别是x在K和-K上的投影,x=x++x-。 对任意x=(x1;x2)∈R×Rn-1, SOC的内部定义为intK={x=(x1;x2)∈R×Rn-1:x1>‖x2‖}。
定义箭形矩阵
其中I是适当维数的单位阵。
定义1(谱分解)[14]对任意x=(x1;x2)∈R×Rn-1, 与SOC相伴的谱分解定义为
x=λ1(x)u(1)(x)+λ2(x)u(2)(x),
其中λi(x),u(i)(x) (i=1,2)分别是x的谱值和谱向量:
λi(x)=x1+(-1)i‖x2‖,
u(i)(x)=
这里ϖ2∈Rn-1是满足‖ϖ2‖=1的任意向量。
定义2[15]对任意x,y∈Rn, 若存在某常数α>0使
〈F(x)-F(y),x-y〉≥α‖x-y‖2,
(2)
则称函数F(x):Rn→Rn强单调。
引理1[12]函数F强单调的充分条件为∇F一致正定, 即存在某常数α>0, 对任意x∈Rn使
xT∇Fx≥α‖x‖2。
2 效益函数
本节提出新SOC权互补函数构造效益函数,并证明其水平集有界性等性质。
首先构造函数:
φτ(x,y)=(1+τ)(x+y)-

(3)
其中:τ∈[0,1),w∈K为给定权向量。 下证φτ(x,y)是SOC权互补函数。
定理1 对任意x,y∈Rn, 函数φτ(x,y)满足
φτ(x,y)=0⟺x,y∈K,x°y=w。
证明(⟸) 若x,y∈K,x°y=w, 则
φτ(x,y)=(1+τ)(x+y)-
(⟹) 若φτ(x,y)=0, 则
(1+τ)(x+y)=
等式两边平方并化简得
(1+τ)2(x2+y2+2x°y)=
(1+τ)2(x2+y2)+8τx°y+2(1-τ)2w,
即x°y=w。 因此
(1+τ)x=
(1+τ)yK|(1+τ)y|-(1+τ)y∈K。
类似可得
(1+τ)y=
(1+τ)xK|(1+τ)x|-(1+τ)x∈K,
故x,y∈K。证毕。
现基于权互补函数φτ(x,y), 构造效益函数
(4)
则求解LSOCWCP(1)可转化为找到无约束极小化问题
minΨ(x)=ψ(x,F(x))
(5)
的全局最小值。
性质1 函数φτ、ψ分别由式(3)和式(4)定义, 令
h=(1+τ)2(x2+y2)+8τx°y+
2(1-τ)2w=(h1;h2)∈R×Rn-1,
(6)
其中:
h1=(1+τ)2(‖x‖2+‖y‖2)+
8τxTy+2(1-τ)2w1,
(7)
h2=2(1+τ)2(x1x2+y1y2)+8τ(x1y2+
y1x2)+2(1-τ)2w2。
(8)

(i) ∇xψ(0,0)=∇yψ(0,0)=0。
(ii) 若(x,y)≠(0,0)且h∈intK, 则
∇xψ(x,y)=
∇yψ(x,y)=


(iii) 若(x,y)≠(0,0)且h∉intK,
(9)
2)∇ψ全局Lipschitz连续, 即对任意(x,y), (a,b)∈Rn×Rn, 存在常数C≥0使得
‖∇ψ(x,y)-∇ψ(a,b)‖≤
C‖(x,y)-(a,b)‖。
3)对任意x,y∈Rn,
〈∇xψ(x,y),∇yψ(x,y)〉≥0,
此等式成立当且仅当φτ(x,y)=0。
4)对任意x,y∈Rn,
∇xψ(x,y)=0⟺∇yψ(x,y)=0⟺φτ(x,y)=0。
证明性质2)~4)的证明可由文献[13]中的引理6和文献[16]中的定理3.1类似得出,这里省略,下证性质1)。
由文献[13]中的命题2知ψ处处连续可微。
(i) 当(x,y)=(0,0)时,
∇xψ(0,0)=∇yψ(0,0)=0。
(ii) 当(x,y)≠(0,0),h∈intK时, 设
λ1(h)=h1-‖h2‖,λ2(h)=h1+‖h2‖
是h的谱值。 对式(6)求导得
∇xh=2L(1+τ)2x+4τy,∇yh=2L(1+τ)2y+4τx,
(10)
故由式(3)、式(4)及式(10)可得结论。
(iii) 当(x,y)≠(0,0)且h∉intK时, 由文献[13]中的命题1类似可证式(9)。证毕。
引理2 设函数φτ(x,y)由式(3)定义, 则对任意x,y∈Rn有
‖φτ(x,y)‖≥
证明将SOC权互补函数φτ(x,y)与x-取内积得
〈x-,(1+τ)(x+y)-z〉=
(1+τ)×[〈x-,x++x-〉+
〈x-,y++y-〉]+〈x-,-z〉=
(1+τ)[‖x-‖2+〈x-,y+〉+
〈x-,y-〉]+〈x-,-z〉。
(11)
因为x-∈-K,y-∈-K, -z∈-K, 所以〈x-,y-〉≥0, 〈x-,-z〉≥0。 又因为y+∈K, 所以〈x-,y+〉≤0。 因此结合式(11)和Cauchy-Schwarz不等式得
‖x-‖·‖φτ(x,y)‖≥
〈x-,(1+τ)(x+y)-z〉≥
(1+τ)[‖x-‖2+〈x-,y+〉]≥
(1+τ)[‖x-‖2-‖x-‖·‖y+‖],
即
‖φτ(x,y)‖≥(1+τ)[‖x-‖-‖y+‖]。
同理可证
‖φτ(x,y)‖≥(1+τ)[‖y-‖-‖x+‖]。
因此
‖y-‖-‖x+‖-‖y+‖)。
证毕。
性质2 假设函数F:Rn→Rn强单调,则对于任意c≥0,水平集Ω={x∈Rn|Ψ(x)≤c}有界。
证明假设存在一个无界序列{xk}⊂Ω。

‖φτ(xk,F(xk))‖→∞,Ψ(xk)→∞,
这与ψ(xk)≤c矛盾, 进而结论成立。
(ii) 当
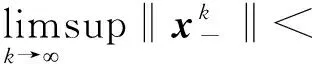

时, 由函数F强单调和引理3.2[17]知Ψ(xk)→∞, 这与Ψ(xk)≤c矛盾,故结论成立。证毕。
3 非单调无导数下降算法
本节给出求解LSOCWCP(1)的非单调无导数下降算法,并证明算法的搜索方向满足下降条件,且全局收敛。
算法1 LSOCWCP的非单调无导数下降算法
步1 选取σ,ρ,β,δ∈(0,1),ε≥0,W0=Ψ(x0),G0=1。 设k=0。
步2 若Ψ(xk)≤ε, 停止。 否则转步3。
步3 计算步长tk=ρmk, 其中mk是式(12)中非负整数m的最小值,
Ψ(xk+ρmdk(βm))≤(1-σρ2m)Wk-
σρ2m(1-βm)×(‖∇xψ(xk,F(xk))‖+
‖∇yψ(xk,F(xk))‖)2,
(12)
其中:
dk(βm)=dk(xk,βm)=
-β2m(1-βm)∇xψ(xk,F(xk))-
(1-βm)∇yψ(xk,F(xk)),
(13)
(14)
Gk=(1-δ)Gk-1+1。
(15)
步4 令xk+1=xk+tkdk(βmk), 置k=k+1。 转步2。
注:本文将ZHU等[10]求解CP的非单调无导数下降算法推广到求解LSOCWCP, 步3采用文献[18]中的非单调线搜索方式计算步长tk, 以提高算法性能。
下证当Ψ(xk)≠0时, 即迭代过程中若xk不是LSOCWCP的解时, 搜索方向dk(βm)满足下降条件:
〈∇Ψ(xk),dk(βm)〉<0。

〈∇Ψ(xk),dk(βm)〉<0,
其中:
∇Ψ(xk)=∇xψ(xk,F(xk))+
∇F(xk)×∇yψ(xk,F(xk))。
证明由∇F(xk)连续及xk∈Ω知,存在常数q>0使得‖∇F(xk)‖≤q。 设
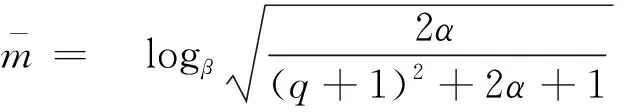

(16)
由式(13)、引理1和性质1(3)得
〈∇Ψ(xk),dk(βm)〉=-β2m(1-βm)·
〈∇xψ(xk,F(xk)),∇xψ(xk,F(xk))〉-
(1-βm)〈∇xψ(xk,F(xk)),∇yψ(xk,F(xk))〉-
β2m(1-βm)·
〈∇F(xk)∇yψ(xk,F(xk)),∇xψ(xk,F(xk))〉-
(1-βm)〈∇F(xk)∇yψ(xk,F(xk)),∇yψ(xk,F(xk))〉≤
-β2m(1-βm)‖∇xψ(xk,F(xk))‖2+
qβ2m(1-βm)·
‖∇xψ(xk,F(xk))‖·‖∇yψ(xk,F(xk))‖-
α(1-βm)‖∇yψ(xk,F(xk))‖2=
(‖∇xψ(xk,F(xk))‖+‖∇yψ(xk,F(xk))‖)2-
β2m(1-βm)(1+q)·
‖∇xψ(xk,F(xk))‖·‖∇yψ(xk,F(xk))‖=
(‖∇xψ(xk,F(xk))‖+‖∇yψ(xk,F(xk))‖)2-
‖∇xψ(xk,F(xk))‖·‖∇yψ(xk,F(xk))‖。
(17)
由式(16)知,式(17)中最后一项的系数为负, 即
(18)
将式(18)代入式(17)得
〈∇Ψ(xk),dk(βm)〉≤

‖∇yψ(xk,F(xk))‖)2≤0。
(19)
又因为式(19)中的等式成立当且仅当
‖∇xψ(xk,F(xk))‖=‖∇yψ(xk,F(xk))‖=0,
所以结合性质1知,dk(βm)满足下降条件,
〈∇Ψ(xk),dk(βm)〉<0。
证毕。
定理3 设函数F强单调,则Ψ(xk)≤Wk, 且算法1适定。
证明先用数学归纳法证明对任意k≥0, 有Ψ(xk)≤Wk。
当k=0时,Ψ(x0)=W0。 假设Ψ(xk)≤Wk, 则由式(12)得
Ψ(xk+1)≤(1-σρ2m)Wk-
σρ2m(1-βm)×(‖∇xψ(xk,F(xk))‖+
‖∇yψ(xk,F(xk))‖)2≤
(1-σρ2m)Wk (20) 由式(14)、式(15)和式(20)得 综上, 对任意k≥0有 Ψ(xk)≤Wk。 (21) 假设式(12)不成立,即对任意非负整数m有 Ψ(xk+ρmdk(βm))-Wk> -σρ2mWk- σρ2m(1-βm)(‖∇xψ(xk,F(xk))‖+ ‖∇yψ(xk,F(xk))‖)2, (22) 将式(22)两边分别除以ρm取极限, 并由式(21)得 σρm(1-βm)×(‖∇xψ(xk,F(xk))‖+ ‖∇yψ(xk,F(xk))‖)2]=0。 这与 〈∇Ψ(xk),dk(βm)〉<0, 矛盾。 因此算法1适定。证毕。 定理4 假设F强单调, 则算法1的生成序列{xk}至少存在一个聚点, 且任一聚点都是LSOCWCP(1)的解。 证明先证{xk}至少有一个聚点。 由式(14)、式(15)和式(20)得 因此{Wk}单调递减。 又因为Wk≥0有下界, 所以{Wk}收敛。 结合0≤Ψ(xk) 下证{xk}的聚点x*是LSOCWCP(1)的一个解, 即证Ψ(x*)=0。 将式(15)代入式(14)得 (23) 化简式(23)得 Ψ(xk+1)=Wk+1+(1-δ)Gk(Wk+1-Wk), (24) 对式(24)两边分别取极限得 (25) 又由式(12)得 0≤σρ2m(1-βm)×(‖∇xψ(xk,F(xk))‖+ ‖∇yψ(xk,F(xk))‖)2≤ (1-σρ2m)Wk-Ψ(xk+1)≤ Wk-Ψ(xk+1), (26) 故由式(25)、式 (26)和夹逼准则得 因此根据性质1知,Ψ(x*)=0。证毕。 运用MATLAB R2014进行数值实验。 在区间[0,10]内随机生成非零密度为10%的稀疏矩阵Q∈Rn×n, 令 P=QTQ+ζI, 其中常数ζ>0,I是维数为n的单位阵。 取向量q=-e, 其中e=(1,0,…,0)T∈Rn, 参数σ=0.1,ρ=0.95,β=0.2,δ=0.1,ζ=1,τ=0.1。 本文以Ψ(x)<10-8为终止准则, 每次实验随机产生10个问题进行求解。 表1和表2中AObj表示效益函数Ψ(x)的平均值, AIter是算法所需迭代的平均次数,ACPU是算法CPU的平均时间。 表1给出维数n=100, 给定不同初始点时, 算法1分别求解LSOCWCP和LSOCCP的数值结果。 表2给出初始点x0=(0;0;…;0)时, 算法1求解不同规模的LSOCWCP和LSOCCP的数值结果。 从表1和表2中均可看出算法1求解LSOCWCP和LSOCCP所需的AIter和ACPU较少, 验证了算法1性能是有效且稳定的。 表1 LSOCCP和LSOCWCP在初始点不同时的实验结果Tab. 1 Experimental results of LSOCCP and LSOCWCP with different starting points 表2 LSOCCP和LSOCWCP在规模不同时的实验结果Tab. 2 Experimental results of LSOCCP and LSOCWCP with different dimensions 本文提出非单调无导数下降算法求解LSOCWCP, 得到良好的数值效果。目前针对LSOCWCP的研究尚不多见, 关于此问题还有很多值得思考的地方, 例如: 如何在更弱的假设下使搜索方向满足下降条件?在将LSOCWCP转化为无约束极小化问题求解时, 如何构造新的效益函数? 此外, 效益函数法虽已应用到一些优化问题中, 但将其用于实际问题的求解还需进一步研究。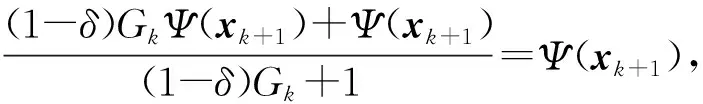



4 数值算例


5 结束语

