求解非线性加权互补问题的光滑算法

汤京永，刘子玉，范 增

(信阳师范学院 数学与统计学院,河南 信阳 464000)

0 引言

2012年,国际著名优化专家POTRA教授提出了加权互补问题(Weighted Complementarity Problem)[1],其数学模型如下:

求(x,s,y)∈Rn×Rn×Rm,使得

x≥0,s≥0,F(x,s,y)=0,xs=w,

(1)

其中F(x,s,y):Rn+n+m→Rn+m是一个连续可微的函数,w≥0为给定的权重向量。

加权互补问题是一个非常广泛的互补系统,其包含并将许多优化问题作为特例。比如,如果

这里T∈Rn×n,A∈Rm×n,b∈Rm,d∈Rn,则加权互补问题即为二次规划

扰动的KKT条件。再比如,如果w=0,m=0并且F(x,s,y)=s-f(x),其中f:Rn→Rn是一个连续可微函数,则加权互补问题就变为标准的非线性互补问题[2-3]：

x≥0,s≥0,s=f(x),〈x,s〉=0。

此外,经济、管理等领域中的许多均衡问题都可以转化成加权互补问题模型，然后进行求解[1]。有些均衡问题可以转化成互补问题(如著名的Fisher均衡问题),将其转化成加权互补问题可以更有效地进行求解[1]。POTRA教授虽然提出了加权互补问题的数学模型(1),但他只研究了线性加权互补问题,即求(x,s,y)∈Rn×Rn×Rm,使得

x≥0,s≥0,Px+Qs+Ry=a,xs=w,

(2)

这里P∈R(n+m)×n、Q∈R(n+m)×n、R∈R(n+m)×m为给定矩阵,a∈Rn+m是给定向量。在文献[1]中,POTRA教授给出了求解问题(2)的两个内点算法,分析了算法的多项式迭代复杂性。2016年,POTRA教授在文献[4]中研究了充分线性加权互补问题,给出了一个预估校正内点算法,证明了算法的迭代复杂性与求解充分线性互补问题内点算法的最好结果相同。最近，ASADI等[5]给出了第一个求解线性加权互补问题的全牛顿步内点法,分析了算法的迭代复杂性。

光滑算法是近年来求解优化问题的一类新方法,其基本思想是利用光滑函数将优化问题等价转化成一个光滑方程组,然后利用牛顿法求解该方程组。与内点法不同,光滑算法可以选取任意初始点,并且在算法实施的过程中不需要迭代点严格可行。因此,光滑算法成为求解优化问题的一类颇受青睐的方法。最近,文献[6-7]分别研究了求解线性加权互补问题(2)的光滑算法,证明了算法具有全局和二阶收敛性质。

本文研究一个求解非线性加权互补问题(1)的光滑算法。具体而言,首先给出一个带有权重的光滑函数,分析函数的性质。利用此光滑函数,将非线性加权互补问题(1)等价转化成一个光滑方程组,然后提出一个新的光滑算法来进行求解。证明了算法生成的迭代点列的任意聚点都是非线性加权互补问题(1)的解,并在非奇异假设条件下证明了算法具有局部二阶收敛性质。不同于文献[6-7]中的光滑算法,本文算法采用了一种非常简单的线搜索技术。数值实验结果表明新算法是非常有效的。

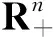
1 一个带有权重的光滑函数

本节给出一个带有权重的光滑函数φc:R3→R,其定义如下:

φc(μ,a,b)=(1+μ)(a+b)-

(3)

其中c≥0是给定的非负整数。

引理1 设φc由式(3)定义,则

φc(μ,a,b)=0⟺a+μb≥0,μa+b≥0,

2(a+μb)(μa+b)=2c+μ2。

(4)

引理2 设φc由式(3)定义,则φc在任意的点(μ,a,b)∈R++×R×R处是连续可微的,并且

(5)

(6)

证明由φc的定义易知φc在任意的点(μ,a,b)∈R++×R×R处是连续可微的,并且

(7)

(8)

(9)

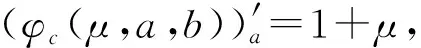
(1+μ)2[(1-μ)2(a-b)2]-

[(1-μ)2(a-b)]2=

[(1+μ)2-(1-μ)2]

(1-μ)2(a-b)2=

4μ(1-μ)2(a-b)2>0,

所以有

从而由式(8)可知式(5)成立。利用同样的方法,可以证明式(6)成立。证毕。

令z=(μ,x,s,y)∈R×Rn×Rn×Rm。定义函数

(10)

其中w=(w1,…,wn)T为权重向量,则由引理1可知H(z)=0当且仅当μ=0且(x,s,y)为非线性加权互补问题(1)的解。此外,由引理2可知,H(z)在任意的点z∈R++×Rn×Rn×Rm处连续可微,并且

其中

为确保雅克比矩阵H′(z)可逆,假设:

假设1已用于分析求解线性加权互补问题(2)的光滑型算法[6-7]和内点法[1,4-5]。

定理1 如果假设1成立,则对于任意的z∈R++×Rn×Rn×Rm,H′(z)可逆。

定理1的证明类似于文献[8]中的定理1,在此省略。

2 算法

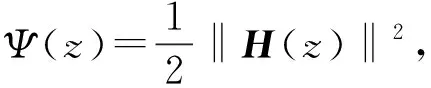
步骤1:如果‖H(zk)‖=0,则算法停止。

步骤2:计算搜索方向Δzk=(Δμk,Δxk,Δsk,Δyk)),使其满足

H′(zk)Δzk=-H(zk)+γβ(zk)e,

(11)

其中β(zk)=min{1,Ψ(zk)}。

步骤3:计算步长αk=δmk,其中mk是满足不等式

Ψ(zk+δmΔzk)≤(1-σδ2m)Ψ(zk)

(12)

的最小非负整数m。

步骤4:令zk+1=zk+αkΔzk和k=k+1,转步骤1。

定理2 如果假设1成立,则算法1产生一个无穷点列{zk=(μk,xk,sk,yk)},并且对所有的k≥0有μk>0。

证明假设对于某个k有zk=(μk,xk,sk,yk)∈R++×Rn×Rn×Rm。由定理1可知H′(zk)可逆,故步骤2是可行的，并且有

Δzk=H′(zk)-1[-H(zk)+γβ(zk)e],

进而可知

Ψ′(zk)Δzk=H(zk)TH′(zk)Δzk=

-2Ψ(zk)+μkγβ(zk)≤

其中第一个不等式成立是由于

下面证明步骤3是可行的。用反证法,假设对所有的非负整数m,都有Ψ(zk+δmΔzk)>(1-σδ2m)Ψ(zk),即

(13)

因为μk>0,Ψ(z)在zk点连续可微。令式(13)两边m→∞,则可得Ψ′(z)Δzk≥0,这与Ψ′(z)Δzk<0矛盾,故至少存在一个非负整数m使得式(12)成立,即步骤3是可行的。因此,在步骤4可得到第k+1个迭代点zk+1=zk+αkΔzk。此外,由式(11)可知Δμk=-μk+γβ(zk),结合β(zk)>0可得

μk+1=μk+αkΔμk=

(1-αk)μk+αkγβ(zk)>0。

(14)

这表明zk+1∈R++×Rn×Rn×Rm。由此可得出结论,如果对于某个k有zk∈R++×Rn×Rn×Rm,则zk+1可由算法1产生,并满足zk+1∈R++×Rn×Rn×Rm。因为z0∈R++×Rn×Rn×Rm,故由数学归纳法可知定理成立。证毕。

引理3 设{zk=(μk,xk,sk,yk)}为算法1所产生的迭代点列,则对任意的k≥0,有

μk≥γβ(zk)。

证明由步骤3和步骤4可知,对任意的k≥0,有Ψ(zk)≥Ψ(zk+1)。因此,如果对于某个k成立μk≥γβ(zk),则由式(14)可知

μk+1≥(1-αk)γβ(zk)+αkγβ(zk)=

γβ(zk)=γmin{1,Ψ(zk)}≥

γmin{1,Ψ(zk+1)}=γβ(zk+1)。

因μ0≥γ≥γβ(z0),故由数学归纳法可知引理成立。证毕。

3 收敛性分析

定理3(全局收敛性) 设{zk=(μk,xk,sk,yk)}是由算法1所产生的迭代点列,则{zk}的任意聚点z*=(μ*,x*,s*,y*)都满足

H(z*)=0。

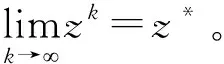
假设Ψ(z*)>0,将导出矛盾。证明分为如下两个部分:

(i) 假设对所有的k≥0都有αk≥c,其中c>0是一个给定的常数,则根据步骤3和步骤4,可得

(1-σc2)Ψ(zk)≤(1-σc2)k+1Ψ(z0)。

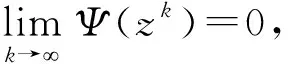
Ψ(zk+δ-1αkΔzk)>(1-σ(δ-1αk)2Ψ(zk)),

故有

-σδ-1αkΨ(zk)。

(15)

根据引理3,有

μk≥γβ(zk)=γmin{1,Ψ(zk)}

对所有的k≥0成立,因此

μ*≥γmin{1,Ψ(z*)}>0,

进而可知Ψ(z)在z*=(μ*,x*,s*,y*)处是连续可微的,故在式(15)两端令k→∞,可得

Ψ′(z*)Δz*≥0,

这里Δz*为方程组

H′(z*)Δz*=-H(z*)+γβ(z*)e

的解。另一方面,根据步骤3可得

(16)

在式(16)两端令k→∞,可得

Ψ′(z*)Δz*≤0。

因此,综合可知Ψ′(z*)Δz*=0。

由步骤2可知，

Ψ′(z*)Δz*=HT(z*)H′(z*)Δz*=

-2Ψ(z*)+μ*γmin{1,Ψ(z*)},

再结合Ψ′(z*)Δz*=0,可得

2Ψ(z*)=μ*γmin{1,Ψ(z*)}。

(17)

利用这些条件,可以从式(17)中推得

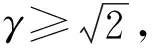
引理4 如果F′为Lipschitz连续,则函数H(z)是在R×Rn×Rn×Rm上是强半光滑的。

证明因为函数φc在R3上是强半光滑的,故由文献[9]中的推论2.4可知结论成立。证毕。

定理4(局部二次收敛性) 假设z*是由算法1产生的迭代点列{zk}的任意聚点。如果所有的V∈∂H(z*)都是非奇异的,并且F′在z*处局部Lipschitz连续,则有

‖zk+1-z*‖=O(‖zk-z*‖2)。

定理4的证明类似于文献[10]中的定理8,在此省略。

4 数值实验

参数取值为σ=0.5,δ=0.2,μ0=10-4,γ=10-5。终止准则为‖H(zk)‖≤10-6。

首先,应用算法1求解如下非线性加权互补问题:

x≥0,s≥0,F(x,s,y)=0,xs=w,

(18)

其中

这里T∈Rn×n,A∈Rm×n,b∈Rm,d∈Rn。注意到,如果w=0,则该互补问题即为二次规划

的KKT条件。

在数值实验中,选择T=diag(rand(n,1)),d=rand(n,1),A=rand(m,n),b=A*rand(n,1),w=rand(n,1)。对于每个问题,随机生成10个算例,使用x0=s0=(1,…,1)T和y0=(1,…,1)T作为初始点进行测试。数值实验的结果列于表1,其中AIT和ACPU分别表示10次测试算法所需迭代次数和CPU时间(以秒为单位)的平均值。由表1可以看出,算法1对于求解非线性加权互补问题是非常有效的。

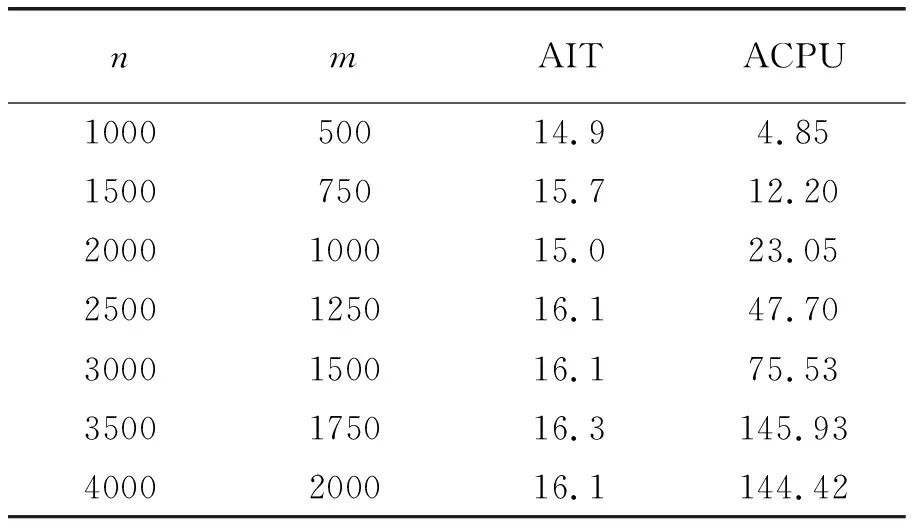
表1 求解问题(18)的数值结果Tab.1 Numerical results for solving problem (18)

下面应用算法1求解由式(2)定义的线性加权互补问题,其中矩阵P、Q、R和向量a定义如下:

表2 求解问题(2)的数值结果Tab. 2 Numerical results for solving problem (2)

5 结束语

基于带有权重的光滑函数,研究了一个求解非线性加权互补问题的光滑算法。该算法在每次迭代时只需求解一个线性方程组和进行一次线搜索。在适当条件下,证明了算法具有全局和局部二次收敛性质。数值实验结果表明算法是非常有效的。