四模块铰接式100%低地板车车体结构强度分析方法

肖玉琪，肖守讷，朱涛，阳光武，杨冰

(西南交通大学 牵引动力国家重点实验室，四川 成都 610031)

0 引言

随着国内城市化的进行，我国城市轨道交通得到了充分的发展，从2010年仅有北京、上海等10个城市开通轨道交通，到2018年全国34个城市总共开通线路达171条，运营车辆达34 012辆[1]；低地板车作为地铁和公交的补充，具有运量大，噪声小、能耗低等诸多优点，在世界各个城市得到了广泛的应用。

传统轨道车辆的设计校核一般根据欧洲标准EN12663—2000，低地板车静强度工况的校核主要参考EN12663—2000[2]和德国BOStrab城市轨道车辆结构要求[3]。低地板车辆不同于传统轨道车辆的地方是没有车钩，而是通过铰链装置这种活动结构传递各车之间的力，通过选用不同自由度的上铰链和下铰链来限制或释放车体的点头、摇头、侧滚运动。通常编组运行，一般两节或三节车为一个固定单元，然后多个单元编组成列运行。

上述特点使得低地板车在结构强度分析时，工程人员需要对车进行复杂的受力分析以及边界条件的分析，而且对于没有经验的工作人员来说，编组建模计算容易出现不收敛的问题。为避免每次编组计算需要进行复杂、繁琐的重复分析过程，可以根据静力学分析，求解出连接各车之间的铰链受力以及车与转向架之间的受力，进而把单节车体从整列车中隔离出来单独分析，最终可以对单车进行加载计算，实现车体结构设计、强度校核快速反馈的工程目的[4]。

1 四编组低地板车

1.1 车型结构特点与主要技术参数

四编组低地板车的编组形式采用(Mc1+Tp1)×(Tp2+Mc2)。四个车体均带有转向架，其中Mc1、Mc2车是带动力转向架的司机室模块，Tp1、Tp2车是不带动力的拖车模块；其中Mc1+Tp1、Mc2+Tp2作为固定的车辆编组单元，用于实验分析、运输以及称重等[5]。

各个车之间通过三种不同自由度的铰接装置连接。编组车辆的下铰链都是使用固定铰，它具有转动自由度，只限制了平动，传递车体间大部分的纵向力、垂向力及横向力；Mc1与Tp1、Mc2与Tp2车之间的上部铰链使用闭合铰，闭合铰可随垂向平动和转动，其余自由度被限制，用来传递部分纵向力和横向力；Tp1与Tp2车之间的上部铰链使用弹性拉杆，只限制了纵向自由度，用来传递车间的纵向载荷。某四编组100%低地板车的编组制式、铰接装置分布如图1所示，其主要技术参数如表1、表2所示。

图1 四编组低地板车编组形式、铰链分布

表1 某四编组低地板车主要技术参数

表2 某四编组低地板车连接装置参数 单位：kN/mm

1.2 拉压工况载荷分析

为考察单车计算方法的实用性和计算精度，以车钩拉伸、压缩两个工况为例，对某四编组低地板车的铰接装置受力、车体和转向架连接结构处的载荷，进行理论推导和有限元整车编组计算。在拉伸、压缩工况推导过程中对模型做出如下的假设与规定[6]：

1)车体是刚体，不发生弹性变形；

2)由固定铰和开放铰连接的Mc1和Tp1车组成的固定编组单元简称为A节车，Mc2和Tp2组成的编组单元简称为B节车；

3)分析计算模型坐标系的xy平面位于轨面，x轴指向Mc1车的行车方向，y轴正向垂直纸面向内，坐标原点位于车辆编组的纵向中心；

4)Mc1车的上下铰链分别简称为JointA、Joint1；Tp1车的分别为JointB、Joint2。

在拉伸、压缩工况中，车体结构不受横向外力，因此可以简化成xOz平面的受力场景，其受力分析如图2所示。

图2 车体拉、压工况受力分析图

从图2的受力分析易知A节车和B节车的受力完全一样，又由于A节车和B节车结构形式、编组单元一样，因此可单独选择A节车或B节车进行受力分析。其中A节车Mc1的受力分析如图3所示。

图3 Mc1车受力分析图

在xOz平面内有：

纵向F1_x+FA_x+F0=0

(1)

垂向F1_z+FS1-G1=0

(2)

力矩FS_1·L1-G1·L11-F0·H0-FA_x·H1=0

(3)

易知此时方程组不是唯一解，假设该工况下Joint1的纵向变形量为Δ1、垂向变形量为Δ2，任意一点相对基点Joint1角位移为θ，二系空簧在重力作用下的压缩量为Δ。则JointA纵向的变形量为XA=Δ1+θ·H1，二系簧的垂向压缩量为Z=Δ+θ·L1-Δ2；将各个铰的刚度值以及变形量带入上述方程可得：

-(K1+K2) ·Δ1-K1· (θ·H1) +F0=0

(4)

-K3·Δ2+K· (Δ+θ·L1-Δ2)-G1=0

(5)

K· (Δ+θ·L1-Δ2) ·L1-G1·L11-F0·H0+

K1· (Δ1+θ·H1) ·H1=0

(6)

K·Δ=G1

(7)

式中：K1、K2、K3、K分别为jonitA 的纵向刚度、joint1的纵向刚度、joint1的垂向刚度、二系簧的垂向刚度，数值见表2；H0、H1分别为车钩受力中心与joint1的高度差、jointA与joint1的垂向高度差；L1、L11分别为二系弹簧、Mc1车质心与joint1的纵向距离。下面方程中的参数类似，不再赘述。

联立上述方程可求得各位置的变形量，进而求解铰接装置、二系簧对车体结构的作用力。

对A节车整体进行受力分析，分析方法同Mc1车，其受力分析如图4所示。

图4 A节车受力分析图

在xOz平面内有：

纵向F2_x+FB_x+F0=0

(8)

垂向F2_z+FS1+FS2-G1-G2=0

(9)

力矩FS1·LS1+FS2·LS2-G1·L11-G2·L22-

F0·H0-FB_x·H2=0

(10)

同理在joint2的位置假设该铰的纵向变形量为Δ3；垂向变形量为Δ4以及任意位置随基点joint2的角位移为β，则JointB纵向的变形量为XB=Δ3+β·H2，Tp1车二系簧的垂向压缩量为Z=Δ+β·Ls2-Δ4，Mc1车二系簧的垂向压缩量为Z=Δ+β·Ls1-Δ4；同时将Mc1车的求解结果FS1的数值代入方程可得：

- (K4+K5)·Δ3-K4·(β·H2)+F0=0

(11)

-K5·Δ4+K·(Δ+β·Ls2-Δ4)+FS2-G1-G2=0

(12)

K·(Δ+β·Ls2-Δ4)·LS1+FS2·LS2-G1·L11-G2·L22-

F0·H0+K1·(Δ3+β·H2)·H2=0

(13)

式中：K4、K5、K6、K分别为JonitA 的纵向刚度、joint1的纵向刚度、joint1的垂向刚度、二系簧的垂向刚度，数值见表2，其余参数如图4所示。

由上述两组方程的联立求解即可解得Mc1、Tp1车的受力，进而可以单独对每节车体进行强度计算校核。

说明：式(7)是一个近似方程，实际上数值有微小的出入。两组方程的Δ数值可以不一样，进行适当修正可使得求解精度更高。

2 编组计算和单车计算对比

基于车钩拉伸、压缩工况，从有限元建模、计算结果、计算效率等角度，对四模块低地板车的单车计算和编组计算进行比较。

2.1 有限元建模

在某有限元软件平台中建立车体结构的计算模型。模型处理：对车体结构的板材、型材等薄壁结构采用相应厚度的壳单元模拟；对铸造件、精加工件使用实体单元模拟；施加于结构质心位置，并使用柔性单元将其连接在相应的安装位置。

边界条件：单车计算时在铰接位置、二系弹簧的安装位置施加上述方程求解的力，然后通过惯性释放法计算即可求解模型。对整车编组计算，在车钩端面施加拉伸或压缩载荷，在二系弹簧的端部施加全约束即可对编组模型进行求解计算。

两种计算方法的有限元模型如图5、图6所示，两个模型的主要信息如表3所示。

图5 编组计算有限元模型

图6 Mc1车单车计算模型

表3 编组、单车有限元模型基本信息

2.2 结果比较

对编组计算的结果进行处理，提取并整理各个铰接装置、二系弹簧上不同方向上的力，将有限元的计算结果和力学方程分析的结果进行比较。求解结果如表4、表5所示。表中：结构受力指该处位置施加给车体的力；“—”表示忽略该处的误差，原因在于该处有限元分析能精确计算车体的弹性变形，本文假设车体是刚体；误差=100%×Abs(编组计算的结构载荷-力学方程计算的结构载荷)/编组计算的结构载荷。

表4 300kN车钩拉伸工况下结构受力分析对比

表5 400kN车钩压缩工况下结构受力分析对比

通过表4、表5可以看出，除了Joint1的垂向荷载误差较大，其余结构各个方向的受力误差很小(基本都在5.00%以内)，具有很好的吻合度。Joint1处纵向受力值远远大于垂向受力值(相差两个数量级)，且垂向受力大小的绝对误差仅为0.893kN，因此可以忽略此处误差对整车结构分析的影响。

在300kN拉伸工况下编组计算和单车加载计算得到的Mc1车体结构应力云图如图7、图8所示。

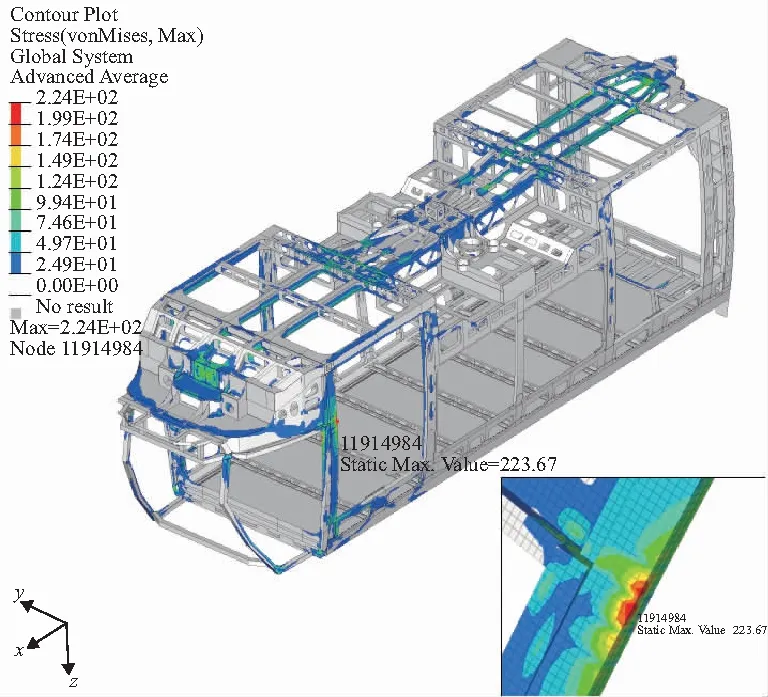
图7 编组计算Mc1车结构应力云图(300 kN)

图8 单车计算Mc1车结构应力云图(300 kN)

在400kN车钩压缩工况下编组计算和单车加载计算得到的Mc1车体结构应力云图如图9、图10所示。

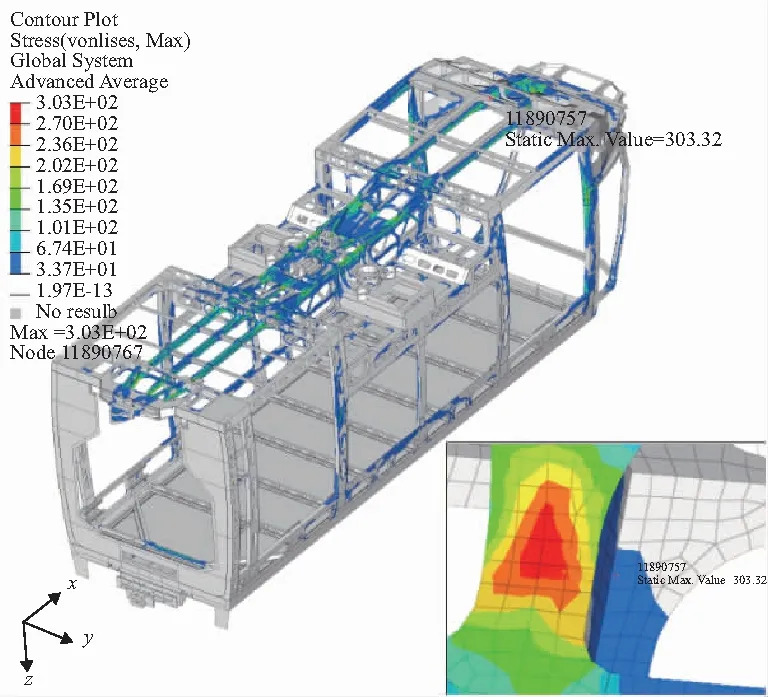
图9 编组计算Mc1车结构应力云图(400 kN)

图10 单车计算Mc1车结构应力云图(400 kN)

从两个工况下的整体结构应力云图可以看出，两种计算方法获得的整体应力分布基本完全一致，两种方法分析的最大应力点位置一样，车钩拉伸、压缩工况的最大应力值分别相差1.52MPa和0.46MPa，此误差基本可以忽略不计。

2.3 计算效率比较

在相同的计算环境下(设备一致、计算参数一致)，编组计算和单车计算反馈Mc1车受力状态的用时对比如表6所示，其中反馈效率=编组计算耗时/单车计算耗时。

表6 计算效率对比

从表6中可以看出，单车计算的效率远远高于编组计算。当在车体设计过程中只需针对TP1或Mc1车进行单独的结构优化，不需要编组计算即可获得单车的应力分布状态，对某工况进行反复计算优化能大大提高反馈以及优化效率。

3 结语

根据某四模块100%低地板车的结构分布、铰接装置的特点，对此结构在车钩拉伸、压缩工况下进行受力分析，获得力学平衡方程，并进行合理假设对方程进行求解。最后用有限元法对车辆进行编组计算，将有限元的求解结果和力学分析的求解结果进行了比较，主要得到以下结论：

1)与编组计算相比，单车计算方法有限元模型的处理更简单，无需考虑铰接装置的模拟、转向架和车体连接装置的模拟以及边界条件的施加，只需在相应的位置施加求解后的载荷即可；

2)编组计算与单车计算所得到最大应力的位置完全一样，数值基本一样，应力分布基本吻合，说明通过力学分析求解连接装置受力的单车计算方法是可行的。

3)单车计算方法对单车受力状态的反馈效率远远高于编组计算，可以很方便地单独对Mc1或Tp1等其他车体进行单车结构的优化设计。

此外本文仅从车钩拉伸、压缩的角度，对编组计算和单车计算进行了对比分析，此方法对其他受力工况同样适用，限于文章篇幅未全部列出。