地铁7号可动心轨道岔动力学仿真研究

田春雨 赵天运

(中铁工程设计咨询集团有限公司，北京 100055)

道岔是实现列车转线、跨线运行的重要铁路设备，也是轨道结构的薄弱环节[1]。列车过岔时，车轮经过的钢轨不平顺，岔区轮轨作用力远大于一般正线[2]。

对于固定辙叉道岔，有害空间会影响列车的行车速度与安全性[3]，列车通过时，需要护轨强制引导车轮运行方向，否则可能导致列车脱轨[4]。许多学者对辙叉区动力响应与结构优化进行研究，陈嵘等通过建立车-岔-桥耦合模型探索辙叉区轮轨接触关系对轨道系统动力响应的不利影响[5]；曹洋等基于轮轨接触几何关系与动力相互作用，提出心轨关键断面轨顶降低值取值方案[6-7]；乔神路等认为，在道岔设计时应尽量采用无缝化处理，以最大程度减小岔区振动噪声[8]；王平等通过理论与试验优化固定辙叉结构[9]。然而，在有害空间处，轨线不连续导致的轮轨关系恶化仍然难以有效解决。为消灭道岔有害空间，可动心轨道岔成为道岔技术的研究焦点[10]。

一般情况下，可动心轨道岔多应用于“大号数”高速道岔中，城市轨道交通“小号数”道岔因过岔速度低、列车轴重轻，多采用成本较低的固定辙叉[11]。地铁车辆段一般占地面积较大，而城市土地的稀缺性使得车辆段上盖物业开发成为必然趋势，但列车进出引起的振动、噪声已成为制约开发的关键因素[12-14]。50 kg/m钢轨7号(50-7号)道岔作为车辆段采用的主要道岔型号，是上盖开发振动噪声的重要来源。目前，鲜有针对其动力学的理论研究，也缺乏7号可动心轨道岔铺设与运营的工程实践，需要通过数值仿真模拟列车通过7号可动心轨道岔时的动力响应，以论证其安全性。

针对地铁A型车、50-7号可动心轨道岔，基于多体动力学建立车辆-道岔耦合动力仿真模型，研究车辆分别以容许速度直逆向、侧逆向、直顺向、侧顺向通过7号可动心轨道岔时的动力学指标变化规律。

1 车辆-道岔动力耦合模型

1.1 可动心轨道岔模型

50-7号可动心轨道岔是目前国内应用可动心轨的最小号数道岔。辙叉采用双肢弹性可弯结构，消除了有害空间，轨道平顺性明显提升，有利于改善轮轨接触关系，延长辙叉使用寿命。50-7号可动心轨道岔全长26.810 m，前长11.194 m，后长15.616 m，导曲线半径150 m，心轨牵引点动程83 mm(见图1)。直、侧向容许通过速度分别为80 km/h、25 km/h。

图1 50 kg/m 7号可动心轨道岔(单位：mm)

道岔模型中，将钢轨视为Timoshenko梁，并充分考虑尖轨及可动心轨变截面的特性，将尖轨与基本轨、可动心轨与翼轨密贴部分视为一股钢轨，采用变截面梁模拟[15]，通过沿线路方向特定位置的钢轨控制断面廓形插值放样实现。将岔枕视为等截面欧拉梁，将扣件简化为弹簧阻尼器，并利用等效刚度和阻尼模拟道岔轨枕与基础的连接[16]。道岔模型尖轨与可动心轨处轨道结构简化模型见图2。

1.2 地铁A型车辆模型

采用地铁A型车进行车辆-道岔耦合系统动力学分析。将车辆系统的车体、构架和轮对简化为刚体。车体与构架之间通过二系悬挂连接，构架与轮对之间通过一系悬挂连接。通过赋予各系悬挂刚度与阻尼对其进行约束与传力，考虑各个刚体点头、浮沉、摇头、横摆和侧滚自由度(整车共35个自由度)，车辆振动模型简化方式见图3。地铁A型车的部分动力学参数见表1。

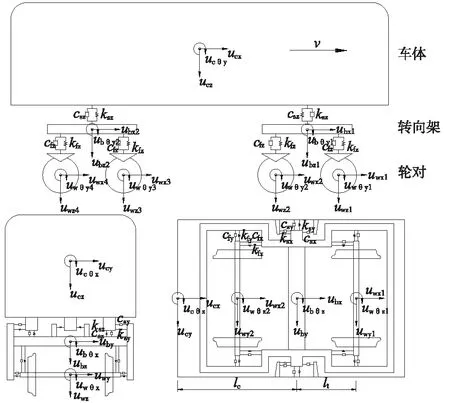
图3 地铁A型车辆简化模型

表1 地铁A型车辆部分动力学计算参数

图4 车辆-道岔耦合模型

耦合系统采用轮轨多点接触模型，蠕滑力采用Kalker滚动接触理论[17]。为使计算更精确，边界设置为道岔两端外100 m，线路总长度230 m，于中段设置7号可动心轨道岔。车辆-道岔耦合模型见图4。

2 动力学评价指标

道岔钢轨自身存在结构不平顺，会使轮轨作用力加剧。为确保车辆能够安全运行，必须分析车辆通过道岔时动力学指标变化[18-19]。根据规范，车辆运行稳定性、运行品质指标见表2。

表2 车辆运行稳定性与运行品质指标

3 车辆过岔动力响应分析

为突出道岔结构不平顺对车辆振动的影响，计算不叠加轨道几何不平顺。以右开道岔为例，分别研究地铁A型车辆以容许通过速度逆、顺向通过50-7号可动心轨道岔时的动力响应。

3.1 直逆向过岔

车辆以80 km/h匀速直逆向过岔时，脱轨系数、轮重减载率、轮轨力、构架加速度等运行稳定性指标变化见图5。

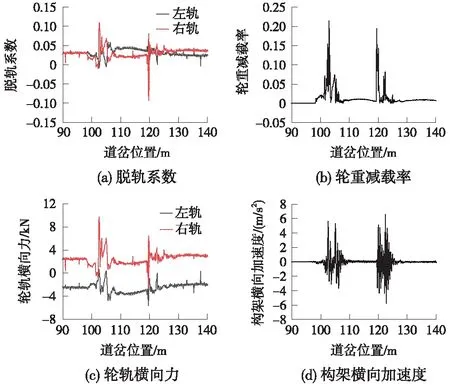
图5 运行稳定性指标

由图5可知，由于轨道平顺，车辆在进入岔区前不会自发蛇行运动，轮缘与钢轨工作边无横向碰撞，左右车轮运行状态同步，轮轨力差异较小，因此脱轨系数和轮重减载率很小，分别为0.03和0；另外，轮轨横向力和构架横向加速度均很小，分别为2.53 kN和0.02 m/s2，车辆运行稳定性良好。

车辆直逆向过岔时，轮轨接触关系开始变化，车辆左轮在直基本轨上运行，而右轮分别经过基本轨、尖轨、导轨、翼轨及长心轨，最后驶离道岔进入区间线路，故右轮各指标变化较大。脱轨系数方面，右轮在经过尖轨时达到最大值0.11，经过可动心轨时为0.08；左轮脱轨系数变化较小，最大为0.07；脱轨系数满足规范要求。轮重减载率方面，轮对经过尖轨与可动心轨时产生较为明显的波动，分别为0.22和0.20，满足规范要求。作为对比，在固定辙叉有害空间处，当车轮由翼轨向心轨过渡时会出现瞬时脱空现象，轮重减载率会瞬时达到1，随后降低[20]。虽然车辆低速过岔时轮重减载率瞬时超限不会影响行车安全，但可动心轨道岔轨线连续的优势可消除这种潜在风险，更有利于行车安全。轮轨横向力方面，右轮的横向力明显更大，在尖轨与可动心轨处达到峰值，分别为9.68 kN和6.16 kN，轮轴横向力小于规范68.30 kN的限值。转向架构架在车辆经过尖轨与可动心轨时发生振荡，横向加速度峰值为6.74 m/s2，满足规范要求。

车辆直逆向过岔时，运行品质指标变化曲线见图6。车体垂、横向加速度峰值为0.08 m/s2和0.14 m/s2，满足规范要求。

图6 运行品质指标变化曲线

3.2 侧逆向过岔

车辆以25 km/h匀速侧逆向过岔时，脱轨系数、轮重减载率、轮轨力、构架加速度等运行稳定性指标变化见图7。车辆侧逆向过岔时，右轮在曲基本轨上运行，左轮分别经过基本轨、尖轨、导轨、翼轨、长心轨及短心轨，最后驶离道岔区域进入区间线路，故左轮各指标变化更大。由于岔区不设超高，车辆侧向过岔时偏载，轮轨接触位置与直向过岔时不同，轮缘与钢轨工作边横向冲击，横向力加剧，导致脱轨系数、轮重减载率等指标整体增大。

由图7可知，脱轨系数方面，左轮在可动心轨处达到最大值0.59，在尖轨处为0.51。由于右轮车辆转向，脱轨系数产生一定波动，最大为0.50；脱轨系数满足规范要求。轮重减载率方面，轮对在导曲线上时，轮重减载率在0.25～0.35范围变化，当轮对驶出导曲线后，轮重减载率逐渐下降，在可动心轨处发生瞬时波动，达到最大值0.34，满足规范要求。轮轨横向力方面，车辆左轮的横向力明显更大，在车轮与尖轨接触冲击时达到最大值52.03 kN，在导曲线上时于48～50 kN范围波动，驶离导曲线后逐渐减小，在可动心轨处因轮轨冲击再次产生峰值31.23 kN；右轮横向力最大值不超过40 kN，轮轴横向力小于规范68.30 kN的限值。转向架构架在车辆经过尖轨与可动心轨时发生振荡，在可动心轨处构架横向加速度瞬时峰值达到5.44 m/s2，振荡后迅速衰减，满足规范要求。

车辆侧逆向过岔时，运行品质指标变化见图8。车体垂、横向加速度峰值为0.05 m/s2和0.35 m/s2，满足规范要求。

3.3 直顺向过岔

车辆以80 km/h匀速直顺向过岔时，动力响应与直逆向过岔时相似，脱轨系数、轮重减载率、轮轨力、构架加速度以及车体垂、横向加速度等指标最大值见表3。车辆直顺向过岔时，右轮在直基本轨上运行，左轮分别经过可动心轨、翼轨、导轨、尖轨及基本轨，最后驶离道岔区域进入区间线路，左轮各指标变化更大。

由表3可知，车辆脱轨系数和轮重减载率均在可动心轨处达到最大值，分别为0.10和0.43；直向过岔轮轨横向力较小，最大为6.55 kN；构架横向加速度最大值为5.40 m/s2；车体垂、横向加速度峰值为0.06 m/s2、0.14 m/s2，各项指标均满足规范要求。

3.4 侧顺向过岔

车辆以25 km/h匀速侧顺向通过道岔时，脱轨系数、轮重减载率、轮轨力、构架加速度以及车体垂、横向加速度等指标最大值见表4。车辆侧顺向过岔时，左轮在曲基本轨上运行，右轮分别经过短心轨、长心轨、翼轨、导轨、尖轨及基本轨，最后驶离道岔区域进入区间线路，右轮各指标变化更大。

表4 车辆直顺向过岔时各指标最大值

由表4可知，相较于直向过岔，车辆侧向过岔时，在辙叉处增加了短心轨向长心轨过渡的不平顺干扰，其轮重减载率略大于直向过岔。由于顺向过岔时导曲线在辙叉之后，辙叉部分轮轨接触主要在钢轨顶面，故可动心轨处横向力与脱轨系数均较小，两者均在尖轨处达到最大值66.23 kN和0.57。构架横向加速度与车体垂、横向加速度也均在尖轨处达到最大值(分别为4.97，0.05，0.33 m/s2)。各项指标均满足规范要求。对比不同过岔方向时的车辆动力响应可以看出，由于车辆偏载和轮轨冲击角的增大，车辆侧向过岔时各稳定性指标整体较直向过岔时大。

综上所述，地铁A型车辆以容许通过速度直逆向、侧逆向、直顺向、侧顺向通过50-7号可动心轨道岔时，车辆运行稳定性、运行品质均良好。

在设计阶段，为突出道岔结构不平顺对车辆振动的影响，未叠加轨道几何不平顺。在实际运营中，轨道几何不平顺也会对岔区车辆动力学指标产生一定影响，下一步将通过在线测试研究该影响下的列车过岔动力响应，以完善50-7号可动心轨道岔的结构设计。

4 结论

针对地铁A型车和7号可动心轨道岔，建立车辆-道岔耦合动力仿真模型，研究车辆分别以容许速度逆、顺向通过7号可动心轨道岔时的动力响应，主要结论如下。

(1)车辆过岔时，各动力学指标均在尖轨与可动心轨处发生波动，较区间线路明显增大，但各指标均满足规范要求，运行稳定性与品质良好。

(2)车辆侧向过岔时，由于车辆偏载，轮缘与尖轨、心轨工作边受横向冲击，轮轨横向力、脱轨系数等指标较直向过岔时明显增大。

(3)可动心轨道岔消除了辙叉的有害空间，优化了轮轨接触关系，车轮由翼轨向心轨过渡时不会出现瞬时脱空现象，更利于行车安全。