可再生能源电源的电能传输线路损耗评估模型分析
吴 健,吴奎华,綦陆杰,冯 亮,孙 伟,杨 波
(国网山东省电力公司经济技术研究院,济南 250001)
随着科技发展和社会步入智能化时代,大量能源被消耗,人类渐渐重视生态环境保护,大量专家学者致力于可再生能源的研究。可再生能源是应用于人类生产、生活中可不断循环再生的能源,如风能、水能、潮汐能,都属于可再生能源[1],可再生能源作为绿色能源受到国家重视,随着不可再生能源不断枯竭,可再生能源将成为人类主要使用的能源。
我国倡导环保节能。能源是国民经济发展命脉,其充分利用可有效降低生产成本,对社会发展具有深远意义。电能是最重要的能源之一,也是用途最广的二次能源,各种可再生能源可转化为电能应用于生活生产中。电力主要通过线路传输,线路传输过程中受到众多因素影响产生损耗[2],输配电线路损耗占电力系统总损耗的1/2,是电力系统中损耗最大部分[3]。线路损耗影响电力系统高效运行,降低电网综合效益,因此精准评估线路损耗不仅可节约能源,降低成本,更具有广大的现实意义。如何评估可再生能源电源的电能传输线路损耗是目前电力系统的主要研究方向[4],同时研究可再生能源电源的电能传输线路损耗评估模型,通过可再生能源电源的电能传输线路损耗评估模型获取精准的线路损耗评估结果,为可再生能源电源的正常运行提供重要依据。
在现有的研究中,学者们依据不同方法提出了可再生能源电源的电能传输线路损耗评估模型。文献[5]提出了遗传算法模型,遗传算法是一种进化算法,可用于寻求最优解,但是在可再生能源电网范围的确定上还有不足,范围界定不准确,导致损耗评估准确率降低;文献[6]提出了一种功率平衡模型,将电源输出功率和电阻消耗功率设定为相等,准确界定了评估的对象,但是没有考虑评估模型中输入、输出样本量纲不同对估计结果的影响,数据适应性差,导致评估精度降低。
基于上述问题,本文提出一种新的可再生能源电源的电能传输线路损耗评估模型。
1 电能传输线路损耗评估模型
1.1 可再生能源电网
可再生能源电网是以可再生能源作为主要电源的电网,利用失衡度界定可再生能源电网。可再生能源电网运行发电功率不确定,因此在电网调度中需要通过不确定的发电功率平衡电网负荷,通过失衡功率节点确定可再生能源电网范围。自然功率是通过不确定性一次能源确定可再生能源电源的发电功率,负荷功率为某一时刻向电力系统取用的电功率总和。
随机t 时刻,用Pu(t)表示可再生能源电源的自然功率,Pl(t)表示可再生能源电源的负荷功率,在可再生能源电网中,其电源的自然功率不确定,负荷功率大小具有随机性。将可再生能源电源与负荷设置为等效负荷,可得不确定性等效负荷功率PΔ(t)=Pl(t)-Pu(t)。电力负荷为用电设备在某一时刻向电网索取的电功率,表现为有功功率和无功功率,而等效负荷功率存在负荷属性[7],所以得出等效负荷功率的范围是PΔ(t)≥0。利用等效负荷将可再生能源电网功率平衡问题转化至可控电源平衡不确定负荷。
设Pc(t)、Pn(t)分别表示可再生能源电网常规电源功率以及网络损失功率,可得可再生能源电网失衡功率公式为

网络损失功率可忽略不计,式(1)可简化为

通过式(2)可知,当ΔP(t)>0 与ΔP(t)<0 时,失衡功率分别为负荷属性以及电源属性[8]。在[t0,t]时段内,由失衡功率ΔP(t)形成的失衡能量E(t)为

失衡功率ΔP(t)与自然功率Pu(t)之比,即可再生能源电源功率损失相对值,用失衡度γ(t)表示。γ(t)的计算公式为

在时间周期[0,T]内,可再生能源电网的整体功率失衡情况用均方根失衡度δ(t)表示,可得年均方根失衡度γY为

式中,T=8 760 h。
通过年均方根失衡度判别电网类型,共存在以下3 种电网:
(1)当γY<10%时,该电网属于低渗透率电网;
(2)当10%≤γY<30%时,该电网属于高渗透率电网;
(3)当γY≥30%时,该电网属于可再生能源电网。
可再生能源电网具有微网、配网、省网、大区网和市网等众多规模,研究可再生能源电源的电能传输线路损耗评估,对于可再生能源电网的规划设计以及调度运行具有重要意义。通过以上方法确定可再生能源电网范围,设计基于可再生能源电源的电能传输线路损耗评估模型。
1.2 传输线路损耗评估方法
可再生能源电网中网线均较长,且电源线路较多,可再生能源电网负荷受时间影响,无法通过恒定电流下独立元件的电能损耗计算方法计算其线路损耗[9],为获取精准的可再生能源电源电能传输线路损耗结果,通过线路等值电阻和线路均方根电流2 个参数,依据电能损耗计算方法获取最终结果。
1.2.1 线路等值电阻
设可再生能源电源中包括若干电阻(R1,R2,…,Rn)的支路,线路中存在的恒定首端电流用IΣ表示。该可再生能源电源的电能传输线路损耗等于不同支路的电能传输线路损耗之和[10],则总电能线路损耗公式为

式中,I1,I2,…,In分别为流经电阻R1,R2,…,Rn支路的电流。
在可再生能源电网中,分支电路的负荷电流较难获取,但负荷点的电量较容易获取,负荷点电量公式为

式中:Ak为负荷点电能;AΣ为首端电能。
通过式(7)可得

式中,Rd为可再生能源电网线路的等值电阻,Rd=。
1.2.2 线路均方根负荷电流
设存在于可再生能源电源线路中的首端负荷电流在不同时间下变化曲线用i=f(t)表示,选取近似方法计算i=f(t),将T 分为n 个时间段Δt,设每个时间段Δt 中负荷均近似于无变化,可得
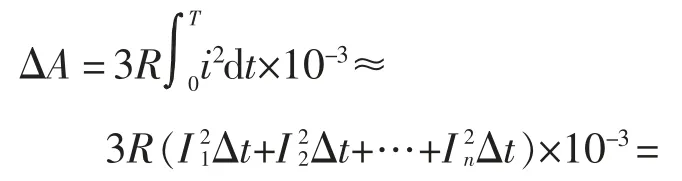
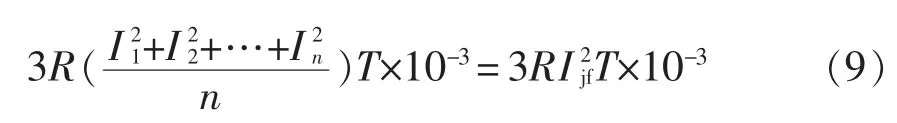
选取电量法作为可再生能源电源的电能传输线路损耗评估模型的理论计算方法[11]。通过电量法获取电能传输线路损耗公式为
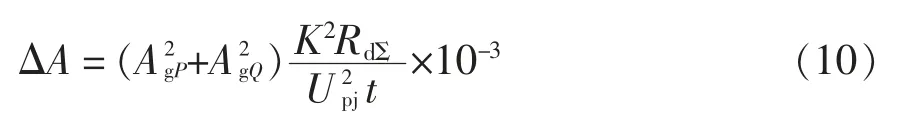
式中:K、RdΣ分别为负荷曲线特征系数以及线路总等效电阻;AgP与AgQ分别为线路有功供电量以及线路无功供电量;Upj为线路平均运行电压。
1.3 核偏最小二乘回归分析的线损率估计模型
确定可再生能源电网范围后,通过上文传输线路损耗评估方法确定模型评估参数,选取线路等值电阻、线路均方根负荷电流、线路有功供电量、线路无功供电量、线路平均运行电压作为模型输入,电能传输线路损耗作为模型输出,以上输入输出样本作为核偏最小二乘回归分析样本。标准化处理输入输出样本后,将处理后的数据利用核函数设置特征向量空间,在特征向量空间中建立可再生能源电源的电能传输线路损耗评估模型,有效评估可再生能源电源的电能传输线路损耗。
1.3.1 样本数据标准化处理
为避免电能传输线路损耗评估模型中输入、输出样本量纲不同影响估计结果,在建立模型前将输入、输出样本数据实施标准化处理保证评估模型评估准确性[12]。对输入、输出样本数据通过零均值方法处理后除以数据标准差,保证评估模型的输入输出样本数据均值与方差均为0 和1。
1.3.2 核偏最小二乘回归建模
本文选取核偏最小二乘回归算法建立电能传输线路损耗评估模型。设存在自变量空间为X={x1,x2,…,xn},利用非线性变换φ(·)将自变量空间映射至高维特征空间F 内,在高维特征空间F 内实施核偏最小二乘回归。采用核偏最小二乘回归算法建立电能传输线路损耗评估模型的核心步骤为引入核函数[13],利用原始输入空间的核函数计算非线性变化后高维特征空间的内积运算,即存在核函数K(xi,xj),利用K(xi,xj)=[φ(xi)]Tφ(xj)实现高维特征空间的内积运算。将原输入空间的非线性运算转化至特征空间的线性运算,过程如下。
1)选择核函数与参数
当函数K(·)符合Mercer 条件时,该函数即可视作核函数。
常用的核函数有高斯核函数、多项式核函数、Sigmoid 核函数等,高斯核函数具有所对应无穷维特征空间的优势,可再生能源电源的电能传输线路损耗样本有限,在该特征空间中为线性可分,因此选取高斯核函数K(xi,xj)=exp(-||xi,xj||2/c)作为所建立评估模型的核函数,其中c 为核参数。利用公式c=rcmσ2选取核参数,其中rc为评估过程中的常数,取1~10,m 与σ2分别表示输入空间维数以及输入数据的方差。
2)确定成分数目
核偏最小二乘回归在通常情况下选取前l 个成分(l≤r)即可获取评估较好的回归模型,选取舍一交叉验证法确定核偏最小二乘回归算法的成分数目。
舍一交叉验证法的具体步骤为:设共存在n 个观测值,每次计算舍去第i 个观测值,且i=1,…,n,利用剩余的n-1 个观测值依据核偏最小二乘回归方法建模[14],且计算抽取第i 个成分后所拟合的回归方程式,获取第i 个观测点上因变量Yj(j=1,2,…,q)的预测值。重复以上步骤,直至i=1,2,…,n,全部验证完毕。
获取第j 个因变量Yj(j=1,2,…,q)在抽取k 个成分后评估残差平方和的公式为

Y=(Y1,Y2,…,Yj)T的评估残差平方和公式为

从1 至r 依次计算抽取成分k 的评估残差平方和[15],令Y 的预测残差平方和为最小值,则k 即为成分数目,l=k。
3)建立评估模型
选取合适的核函数并确定成分数目后,利用核函数建立回归模型,即

通过回归模型可得预测模型为
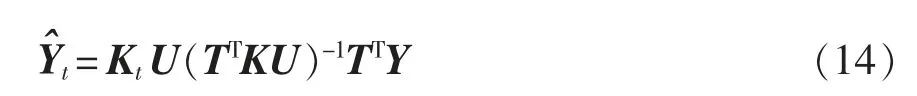
式中:U 由成分u 组成,可表示为U={ui}i=1,2,…,m;T 由成分t 组成,可表示为T={ti}i=1,2,…,m,其中ui、ti均为第i 次提取成分;K 与Kt分别为回归矩阵以及测试矩阵,其中Kj=K(xt,xj)表示矩阵中元素;{xj}表示样本数据,且j=1,2,…,n。
2 实验分析
在Matlab 仿真平台中模拟某地区可再生能源电网,采用本文所提模型评估可再生能源电源的电能传输线路损耗情况,检测本文所提模型的评估性能。采用本文模型评估可再生能源电源的电能传输线路损耗初始界面如图1 所示。

图1 本文模型评估电能传输线路损耗初始界面Fig.1 Initial interface of power transmission line loss evaluation using the proposed model
Matlab 仿真平台所模拟地区可再生能源电网供电面积为1.7×108m2,电源点布置的分区分压情况如表1 所示。采用本文模型评估该可再生能源电网供电区域4 个分区在2018 年12 月1 日的电能传输线路损耗情况,结果如表2—表5 所示。

表1 全网分区分压设备数据统计Tab.1 Data statistics of voltage division equipment in different zones in the whole network

表2 A 区电能传输线路损耗评估结果Tab.2 Evaluation results of power transmission line loss in Zone A
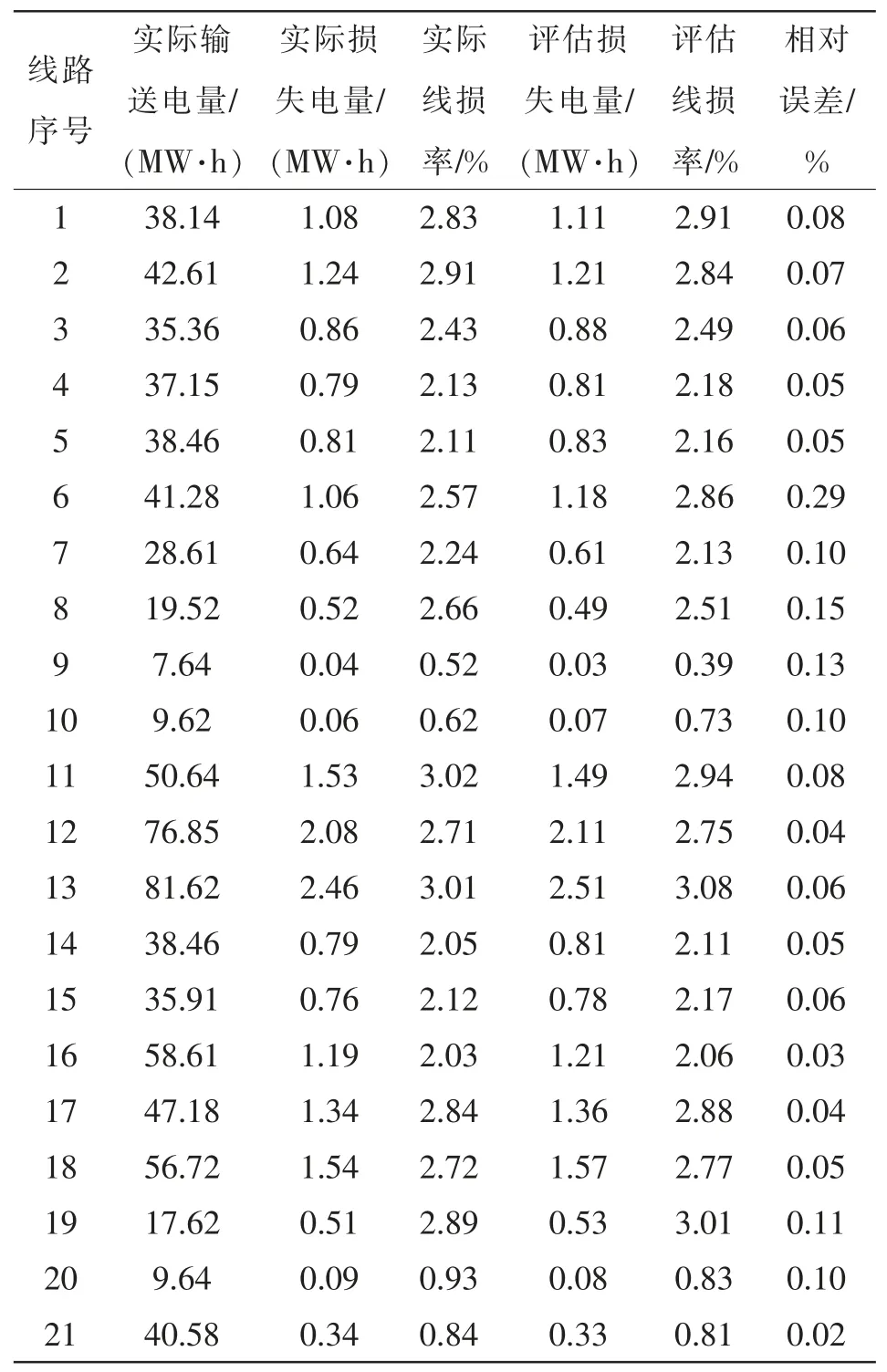
表3 B 区电能传输线路损耗评估结果Tab.3 Evaluation results of power transmission line loss in Zone B
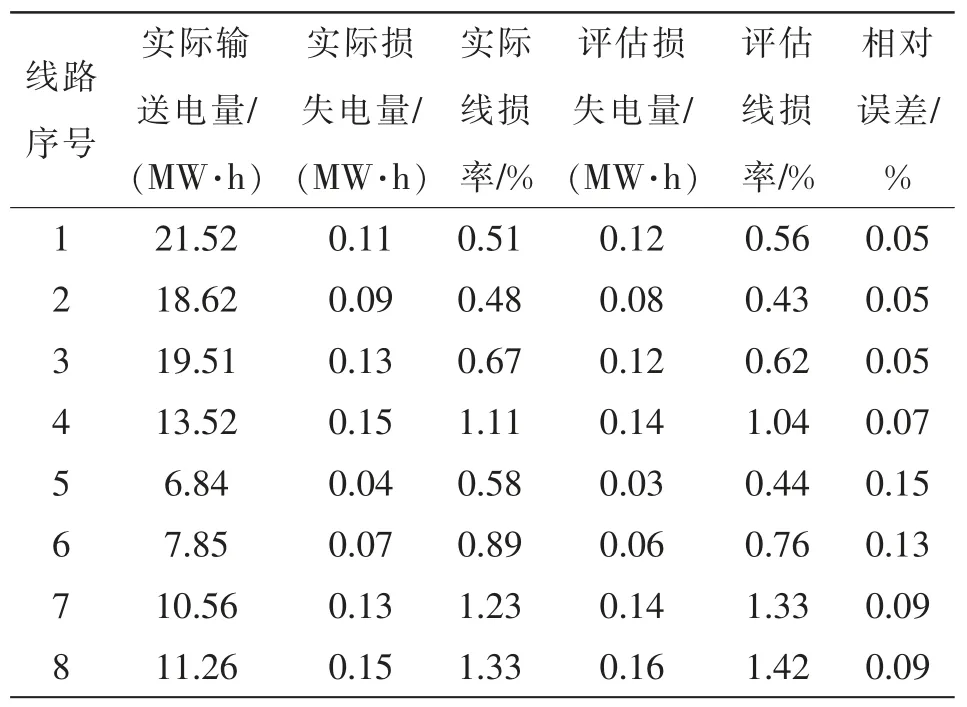
表4 C 区电能传输线路损耗评估结果Tab.4 Evaluation results of power transmission line loss in Zone C
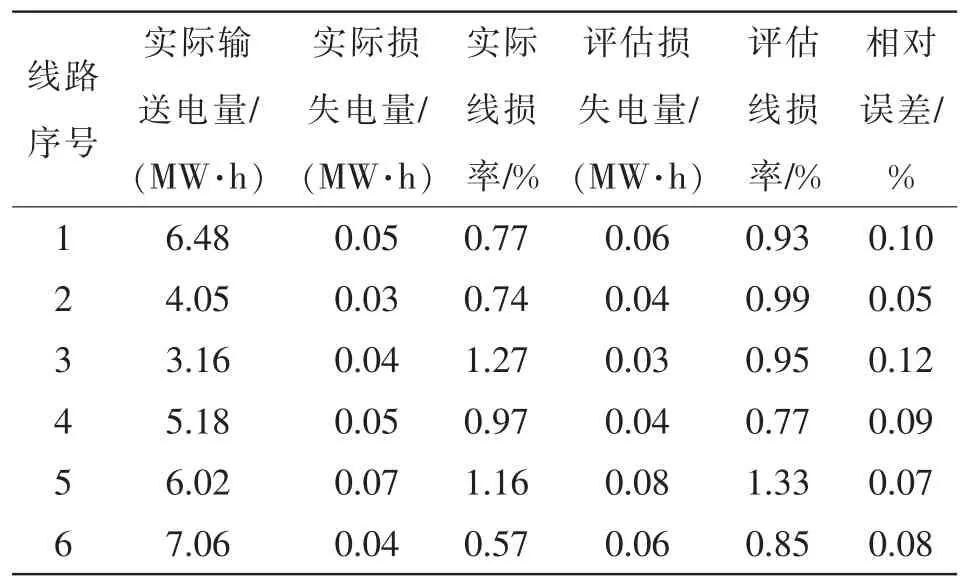
表5 D 区电能传输线路损耗评估结果Tab.5 Evaluation results of power transmission line loss in Zone D
通过以上实验结果可以看出,采用本文模型可有效评估2018 年12 月1 日可再生能源电源不同区域各支路的电能传输线路损耗,且评估误差较低,评估4 个区域的电能传输线路损耗误差均在0.5%以内,验证了本文模型的评估精度。
为进一步验证本文模型的评估精度,评估该电网2018 年12 月3 日至12 月9 日的电能传输线路损耗,并将本文模型与文献[5]和文献[6]模型对比,据此得出评估结果如图2 所示。
图2 实验结果表明,采用本文模型评估可再生能源电源的电能传输线路损耗评估准确率较高,在评估12 月3 日—12 月9 日的电能传输线路损耗评估相对误差均在1%以下,而文献[5]和文献[6]模型评估准确率明显低于本文模型,文献[5]和文献[6]模型评估12 月3 日—12 月9 日的电能传输线路损耗评估相对误差均在1%以上,验证了本文模型的评估精度。采用本文模型评估可再生能源电源的电能传输线路损耗评估结果与真实值非常接近,说明本文模型适用于可再生能源电源电能传输线路损耗评估实际应用。

图2 3 种模型评估结果对比Fig.2 Comparison of evaluation result among three models
为进一步验证本文模型的评估性能,比较文献[5]和文献[6]模型以及本文模型在不同迭代次数下的适应能力,对比结果如图3 所示。
通过图3 实验结果可以看出,采用本文模型评估可再生能源电源的电能传输线路损耗时,在迭代次数为30 时即趋于稳定,而文献[5]和文献[6]模型在迭代次数为50 次时才趋于稳定,且本文模型的适应度在不同迭代次数下均高于文献[5]和文献[6]模型,验证了本文模型的全局收敛能力,再次验证了本文模型评估的有效性。

图3 适应能力对比Fig.3 Comparison of adaptability
本文模型相较于文献[5]和文献[6]模型,引入失衡度,通过失衡功率节点确定可再生能源电网范围,缩小了评估范围,排除了区域外的差异点,减小了范围外差异点对评估的影响。并考虑评估模型中输入、输出样本量纲不同对估计结果的影响,提高了数据适应性。构建核偏最小二乘回归模型,利用核函数确定成分数目,完成最后的误差评估,实验结果表明,本文模型具有较好的评估效果,评估具有可行性。
3 结语
研究基于可再生能源电源的电能传输线路损耗评估模型,选取线路等值电阻、线路均方根负荷电流、线路有功供电量、线路无功供电量、线路平均运行电压作为模型输入,电能传输线路损耗作为模型输出,利用核偏最小二乘回归方法建立评估仿真模型,实现可再生能源电源的电能传输线路损耗评估。仿真结果表明,所研究模型具有较高的评估精度和较强的适应能力,说明该模型可应用于实际可再生能源电网中,为制定可再生能源电源的电能传输线路损耗计划提供有效依据。

