永磁同步电机全域非稳态温度场数值模拟方法

梁志强

(沈阳工业大学，辽宁 沈阳 111003)

1 引言

永磁同步电机一直都是电气工程装备领域的重点研究对象，相较于其它种类的电机，永磁同步电机具备较大的功率密度，而物理尺寸则比同功率的低速、中速电机小得多[1]；转动时的惯量很小，而动态响应却很快；能够直接对高速负载进行驱动，不需要装载传统的变速机械装置，可以避免装载变速机械装置带来的噪声、振动与损耗，减少设备维护成本与设备自身体积，提升传动系统的精度与效率[2]。然而永磁同步电机体积小的这一优势也会带来难以迅速散热的问题，特别是在电机自身温度较高的时候，会严重影响各部件的工作性能，使电机的效率、出力、性能等无法达到定值，从而影响电机的运行安全。克服该问题需要深入研究永磁同步电机的全域非稳态温度场，并对其实施数值模拟[3]。

当前的传统永磁同步电机全域非稳态温度场数值模拟方法包括基于流固耦合的永磁同步电机全域非稳态温度场数值模拟方法[4]、基于功热等效的永磁同步电机全域非稳态温度场数值模拟方法[5]以及基于偏微分方程的永磁同步电机全域非稳态温度场数值模拟方法[6]。然而三种传统方法的模拟结果精度不能满足永磁同步电机的温度场数值模拟的要求。因此针对该问题设计一种新的永磁同步电机全域非稳态温度场数值模拟方法。

2 温度场数值模拟

2.1 获取导热方程

首先根据热传递与能量守恒相关定理获取多方向热量传递时的实际热传递的能量

q=-λgradT

(1)

其中，q代表热传递的具体热流量；λ代表导热率；gradT代表相邻的两个物体间存在的具体温度差。

对于永磁同步电机来说，其生成的热量包括损耗涡流热量、铁耗热量以及铜耗热量，均为向外发散，因此其电机生成项增加值为正数，则永磁同步电机的具体生成热量为

Q=q·gradT

(2)

其中，Q代表电机具体生成热量。

将永磁同步电机分成多个电机微分单元，如果其产生内部损耗从而发热时，在直角二维坐标系内，其三个轴均会传递热量，这些传递热量能够利用下式来表示

(3)

其中，QΔx、QΔy、QΔz代表三个轴的传递热量；Qx+Δx、Qy+Δy、Qz+Δz代表三个轴的总接收热量；Qx、Qy、Qz代表三个轴的散失热量[7]。

在微分单元中，各单元所产生的总具体热量如下

(4)

其中，Qs代表各单元所产生的总具体热量；ρ代表热传导材料的密度；Cp代表材料的具体比热容；t代表产生热量的初始时间；gradTx、gradTy、gradTz分别代表三个轴方向的温度差。

则由能量守恒相关定理，永磁同步电机产生的内部热能是

Qin-Qout+Qv=Qs

(5)

其中，Qin代表物体实际吸收热量；Qout代表物体实际发散热量；Qv代表物体实际传递热量。

也就是微分单元内具体能量变化能够用下式表示

-QΔx-QΔy-QΔz+q=Qs

(6)

对该公式实施傅里叶分解，具体如下式

(7)

其中，qx、qy、qz代表三个轴的具体能量变化。

可以得到下式

(8)

(9)

将式(7)、(8)带入式(9)中，可得最终得到导热方程为

(10)

2.2 获取边界条件

接着获取永磁同步电机全域非稳态温度场的边界条件，通过对电机模型实施假设，准确获取其边界条件。对永磁同步电机模型实施如下假设，具体假设内容如表1所示[8]。

表1 模型假设内容

则式(8)可以简化为下式

(11)

根据上式可知，永磁同步电机构成材料的具体温度值与空间具体变化量、介质温度具体传递时间有关，对该方程进行求解需要以对边界条件进行限制，三种限制边界条件的内容为：

第一种限制边界条件：永磁同步电机传热边界所对应的温度函数为已知

T|Γ=T0

(12)

其中，Γ代表永磁同步电机的边界；T0代表导热时假设的永磁同步电机表面温度，该数值既可以是恒定的数值，也可以是变动的数值[9]。

第二种限制边界条件：永磁同步电机边界面所对应的热流密度值为已知

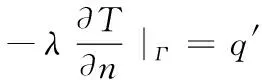
(13)

其中，n代表边界面数量，为正整数；q′代表永磁同步电机边界Γ所对应的热流密度值。

当永磁同步电机存在不导热的传导面时，式(11)可以用下式来表示

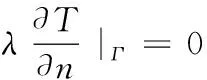
(14)

第三种限制边界条件：流体温度已知是Tf，并且已知永磁同步电机表面与流体的实际交换系数已知

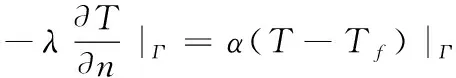
(15)

其中，α代表永磁同步电机边界外流体的具体温度[10]。

2.3 构建全域非稳态温度场计算模型

使永磁同步电机工作于自然条件中，对其实施全域非稳态温度场的实时分析，在分析中仅考虑对流换热以及热传导问题，忽略永磁同步电机产生的辐射。结合分析结果与热传导理论，构建永磁同步电机全域非稳态温度场计算模型的方程，具体如下式所示

(16)

其中，Kx、Ky、Kz代表各种介质的具体导热系数；c代表材料热容；γ代表材料密度；τ代表材料导热时间；S1代表绝热的对应边界面；S2代表散热的对应边界面；Te代表介质的具体温度；K代表具体的导热阈值[11]。

对该方程实施数学分析，然后通过等价变分构建永磁同步电机全域非稳态温度场的计算模型，构建的模型具体如下式所示

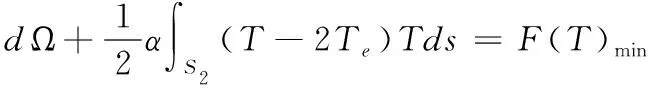
(17)

其中，F(T)代表永磁同步电机全域非稳态温度场的计算模型；Ω代表转子转速；d代表齿距；s代表热交换范围。

为了使永磁同步电机全域非稳态温度场三维模型适用于大部分情况，需要对其实施永磁同步电机的条件规定，具体如表2所示[12]。

2.4 全域非稳态温度场数值模拟

在有限元分析软件中输入构建的全域非稳态温度场计算模型，构建全域非稳态温度场三维模型。对该三维模型实施损耗分析，融合永磁同步电机的整体数据，以计算其各部分的具体生热率，将计算数据加载到该三维模型中，实施全域非稳态温度场数值模拟，获取永磁同步电机全域非稳态温度场的具体分布状况。

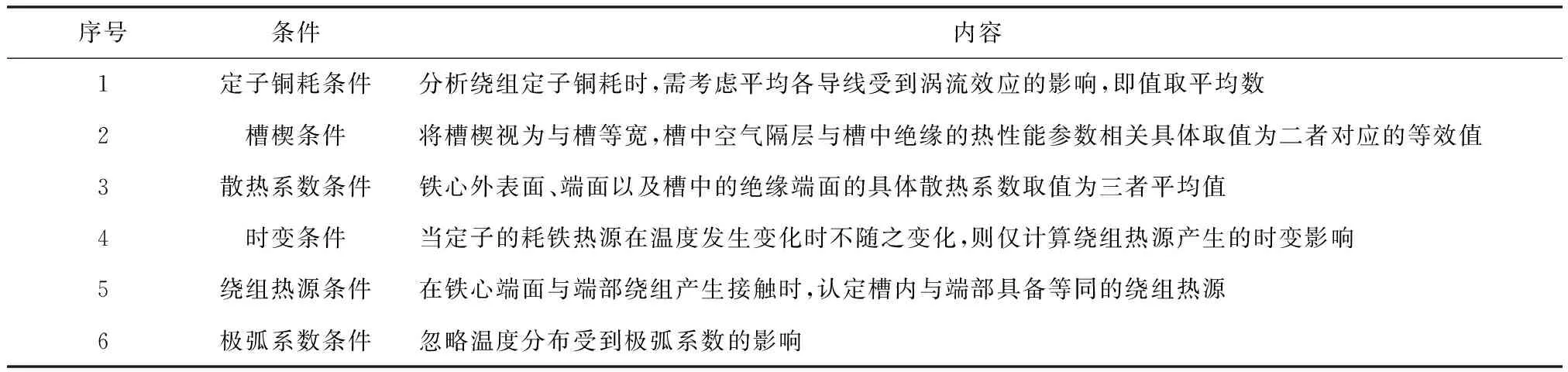
表2 永磁同步电机的条件规定

获取的永磁同步电机中定子的全域非稳态温度场具体情况如图1所示。

图1 定子的全域非稳态温度场具体情况

根据图1，定子最高轭部温度为202℃，最低轭部温度为124℃。

获取的永磁同步电机中电机绕组的具体温度场分布状况如图2所示。

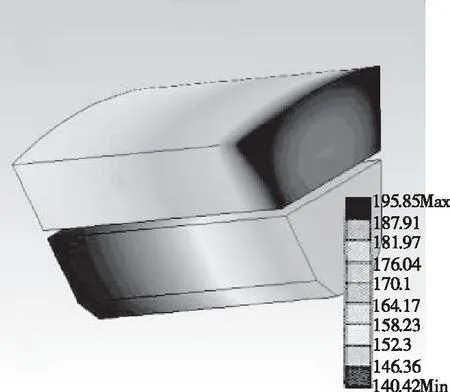
图2 电机绕组的具体温度场分布状况

根据图2，绕组接近定子的外侧部分可达很高温度，约为192℃，而绕组接近气隙部分的温度则较低，约为140℃。

而获取的永磁同步电机中永磁体的具体温度场分布状况如图3所示。

图3 永磁体的具体温度场分布状况

根据图3，永磁体的端部温度达到最高为127℃，温度最低之处为中间部分，为121℃。

3 实验分析

3.1 实验设计

利用设计的永磁同步电机全域非稳态温度场数值模拟方法，进行永磁同步电机全域非稳态温度场数值模拟实验。选择四个相同型号的永磁同步电机作为实验电机，利用测量反电势与绕组电阻的方式对实验电机的转子与电机绕组等的温升进行测量。实验用永磁同步电机的额定转矩是1.04N·m，而转速则设为每分钟一万转。实验平台为传感器三次谐波控制平台，平台载波频率约为30kHz。电机的实验波形包括过零点三次谐波信号与电流A相波形。实验永磁同步电机槽数所对应的各种损耗数据具体如表3所示。

表3 槽数所对应的各种损耗数

在永磁同步电机全域非稳态温度场数值模拟实验中，为了保障实验结果具备对比性与可信性，将传统永磁同步电机全域非稳态温度场数值模拟方法与所设计的永磁同步电机全域非稳态温度场数值模拟方法进行对比实验，其中传统永磁同步电机全域非稳态温度场数值模拟方法包括基于流固耦合、基于功热等效方法。

3.2 生热率计算准确性对比

生热率对永磁同步电机温度场数值模拟结果有着重要影响，因此以生热率计算准确性为实验对比指标，将三种方法进行对比，对比结果如图4所示。

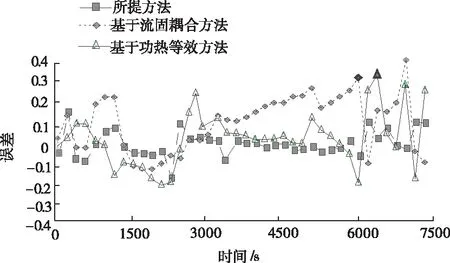
图4 生热率计算误差

分析图4可知，所提方法的生热率计算误差均小于两种对比方法，最高误差不超过0.2，而基于流固耦合方法与基于功热等效方法的最高误差可达到0.4左右。因此说明所提方法可以准确计算永磁同步电机的生热率，以对其温度场数值进行准确模拟。

3.3 升温情况对比

比较各个实验永磁同步电机全域非稳态温度场数值模拟方法的数值模拟性能，即四种实验方法分别对应一个实验永磁同步电机，并对其进行全域非稳态温度场数值模拟，获取其数值模拟结果。比较各个实验电机数值模拟结果与永磁同步电机全域非稳态温度场实际升温结果，观察各个模拟方法的数值模拟结果与实际升温结果是否相近，越相近证明该永磁同步电机全域非稳态温度场数值模拟方法的数值模拟性能越好。

传统永磁同步电机全域非稳态温度场数值模拟方法与所设计的永磁同步电机全域非稳态温度场数值模拟方法的数值模拟性能实验结果具体如图5所示。

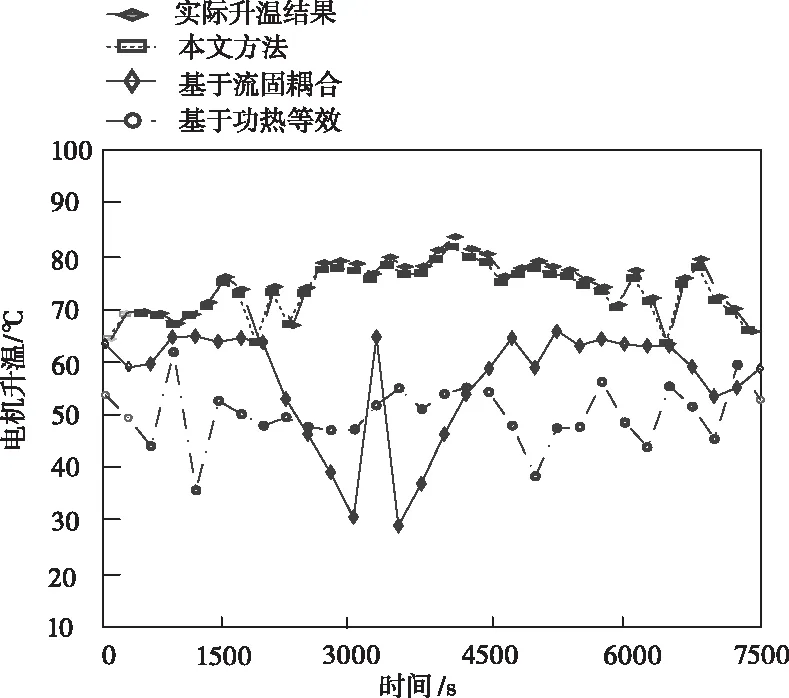
图5 数值模拟性能实验结果

根据图5的数值模拟性能实验结果，所设计永磁同步电机全域非稳态温度场数值模拟方法的数值模拟结果，与永磁同步电机全域非稳态温度场实际升温结果最为接近。也就是所设计的永磁同步电机全域非稳态温度场数值模拟方法的数值模拟性能优于传统永磁同步电机全域非稳态温度场数值模拟方法。

4 结束语

为了提高永磁同步电机的工作性能，对永磁同步电机全域非稳态温度场数值进行模拟研究，永磁同步电机全域非稳态温度场数值模拟方法通过构建全域非稳态温度场计算模型实现了永磁同步电机的全域非稳态温度场数值模拟，并且实现了数值模拟性能的提升，对于减轻电机运行损耗有很大意义。