基于聚类挖掘的移动通信网络链路优化设计

陈俊霖，齐继东，鲜 娟*，邓 娟

(1. 重庆邮电大学移通学院，重庆 合川 401520；2. 重庆邮电大学，重庆 400065)

1 引言

随着移动网络通信迅速技术发展，人们将注意力从网络通信设计的拓扑优化、信道容量的合理分配等问题转向了应充分利用信道能力，减少虚耗现象，从而使移动通信网络链路优化设计成为重点。链路优化是将网络与信息传输紧密联系的重要桥梁，通信网络中的链路优化表示根据尚有的网络节点与结构特征，对节点连接方式进行优化。由于移动网络通信结构较为复杂，且统计数量庞大，很难对不同机制的性能进行比较，而链路优化可以为其提供平台，有助于提升复杂通信网络的稳定性。传统链路优化方法对节点密度影响考虑较少，在节点密度超高时，链路优化的性能会大大降低，为此相关学者对移动通信网络链路问题做了大量研究。

文献[1]提出基于高阶近似的链路优化方法。首先对通信网络的归一化相邻矩阵与相似度矩阵进行构建，并分解相似度矩阵，获得节点表示的向量数值；其次利用高阶网络对相似度矩阵进行优化处理，并获取更高阶矩阵函数表达式，最后通过在真实数据集合中的多次试验，将优化后的链路与原始链路对比，证明该优化方法的可行性。

文献[2]在高负载MANET环境下，提出基于灰色区域估计的自适应链路优化方法。通过对基于卡尔曼滤波的灰色区域预测分析，计算通信过程信噪比，判断链路状态情况，并在链路发生失效之前，重新选择新路由，提高效率；处理通信网络中的灰色区域，利用多路径冗余传输方式提高链路性能的同时改善网络通信质量。

虽然上述方法在一定程度上改善了链路性能，但是在通信过程中，传输功能受到带宽限制，基于此，本文在聚类挖掘基础上对移动通信网络链路优化进行设计。聚类挖掘算法是根据统计学的聚类分析方法对数据信息进行挖掘。通过对聚类挖掘各项指标的分析，获取节点特性，判断链路最佳带宽值，根据非线性规划原理实现链路优化设计。所提方法能够提升通信节点带宽，减少节点拥塞现象发生，实现移动通信网络链路优化。

2 方法

2.1 通讯网络聚类挖掘算法原理

对一个移动通信网络G(V，E)进行定义[3]，V表示节点集合，E为链路集合。网络节点总数量与总边数，分别表示为N与M。假设U是数量为U(N-1)/2个节点构成的集合，则U-E为网络中缺失的链路集合。链路优化就是要达到在U-E集合中筛选出失效链路，此时需要设定链路估计方法，对不发生连边现象的节点(x，y)给予分数值Sx，y。此分数值具有接近性特征，它和节点联通的概率成正相关。将失效链路按照分数高低进行降序排列，分数越高，证明失效可能性越大。

其链路优化过程如下述内容所示：

1)在通信网络中存在节点x，将其附近集合表示为Γ(x)，节点x与y的相似程度可以表示它们相同的邻近节点数量[4]。

2)通过两个节点相同邻近节点数量在节点总数量中所占比重，对节点x与y的相似性进行描述

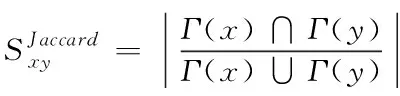
(1)

式中，Γ(y)表示通信网络中的节点y附近集合。

3)按照最佳比例权重对邻近集合中的节点进行合理分配[5]，任意节点的权重表示为

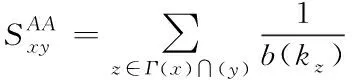
(2)

4)作为通信网络整体结构的估计方式，对网络中全部路径进行考虑。其表达式为

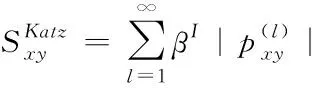
(3)

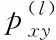
5)利用x与y节点之间存在的不同路径数量，描述节点之间相似度。表达式为

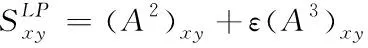
(4)

式中，A描述邻接矩阵，ε表示自由参数。

6)将共同邻近节点数据以节点聚类系数的方式体现出来，把x与y节点存在的相似度作为邻近节点的系数之和

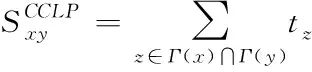
(5)

式中，tz表示经过节点z的三角形个数。

2.2 聚类边信息获取

通常情况下，聚类信息可以表示节点聚类系数[6]，但是聚类系数代表的是全部预测节点，并不是局部的，因此对于不同节点，所得到的预测值相同。这会影响对链路性能的判断，因为不同节点在相同的局部网络通信情况下拥有与其对应的聚类信息。

由于边可以提供很多局部信息特征，因此本文利用边聚类信息，通过与相似度指标的结合，判断边聚类信息在估计链路性能方面的作用。边聚类数可以表示为

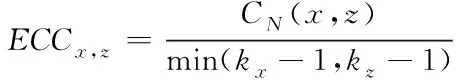
(6)

式(6)中，CN(x，z)代表穿过链路(x，z)的三角形个数，kx、kz分别代表节点x、节点z的度。该表达式也可描述节点x对节点z的聚类系数容纳度。

三元闭包是通信网络中最根本的局部特征与连接机制，平衡性与稳定性较强[7]。所以本文对估计节点存在的端节点和邻近节点的性能加以分析，完成挖掘闭包机构存在的信息特征，因此式(6)能简化为以下表达式

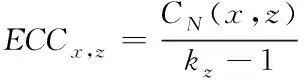
(7)

融合节点的数量会对边的聚类系数造成影响，因此对链路相似性进行定义，相似性指标表达式如下所示

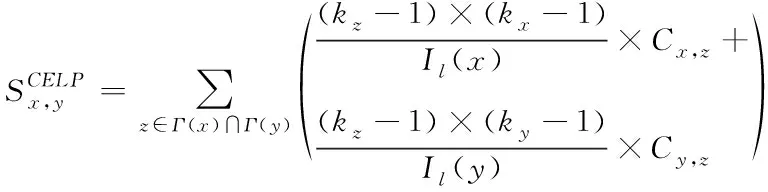
(8)

由式(8)简化得到下列公式

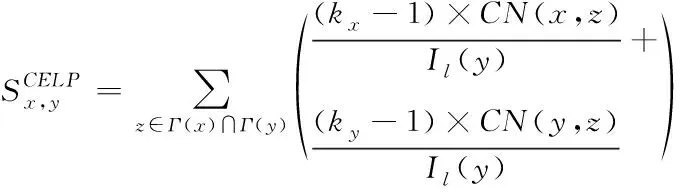
(9)

上述公式中，相乘因子的首个分量是邻近节点z和端点x造成的影响占比，将该值与边聚类系数相乘可以获得估计链路的局部信息特征量。所以指标为邻近节点z在通信网络中x与y节点链路的信息贡献总和。节点与链路是移动通信网络的两个关键角度。广泛挖掘节点自身和边构成的局部结构对估计链路的价值，有显著优势。

2.3 通信网络链路优化设计

2.3.1 节点状态判断

根据上述节点对链路存在的价值和节点状态进行判断。由于移动通信网络的移动节点寻在较强的流动性[8]，因此节点之间只能利用一对一的方法进行信息交互。即不相同节点的信息交互都不由自身区域中的节点传输，所以链路存在间断性特点，在任意节点和某个节点进行交互时，取得的链路信息并不是完整的。针对上述问题，本文利用本地节点对链路信息进行实施检测，再通过马尔科夫信道转移模型完成链路建模，结合采样时间段和本地节点相关的信息交互节点状态，构建矩阵模型。

因为全部节点运动状态的性质都属于有限移动状态，节点运动环境与最大速度都能够进行测量，并且区域与运动速度不同导致信噪比也随之产生变化，信噪比情况可以表示为多个持续状态

T={T1，T2，T3，…Tn}，Tn∈[Ωn，Ωn+1]

(10)

式中，[Ωn，Ωn+1]表示不同信环境中信噪比取值范围，设定信道属于瑞利信道，衰落情况为缓慢衰落，并且节点所在的信道较为稳定，没有跳变情况出现，节点信道存在的信噪比范围只会持续变化，因此节点所在的不同信道中具有的转移概率Sn，n+1表示为

Sn，n+1=St{St+1=n+1|St=n}

(11)

式(12)中，St代表在t时间段上节点的信噪比情况，Sn，n+1为节点从t时间点移动到t+1时间点上信噪比的变换情况。

由于节点信道全部符合瑞利分布状态要求，因此节点在实现信息传输时[9，10]，传输规律都属于瑞利变换规律，假设信噪比是ni(x)，则ni(x)计算模型表示为

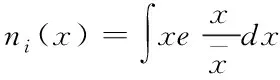
(12)

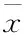
结合式(10)，获得节点在兴状态时[Ωn，Ωn+1]的概率ni(n)表示为

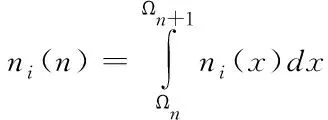
(13)

为方便对式(13)进行计算，对函数F(x)进行下述定义

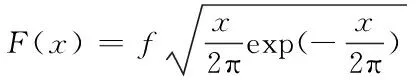
(14)

由以上公式可知，假如节点处在[Ωn，Ωn+1]状态，则在t+1时间点上状态转移的概率ni(n)表达式如下

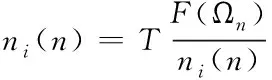
(15)

式(15)中的f表示现有节点的频率转移情况，式(15)T表示节点运动情况变化周期。

结合式(15)获得节点状态更迭的变化矩阵I表示为

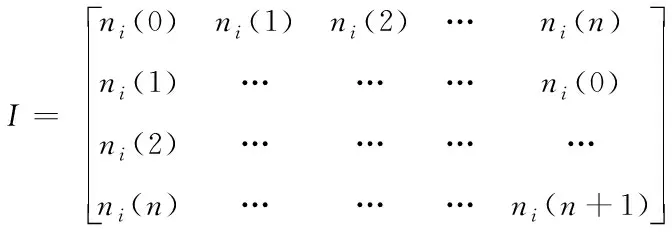
(16)

2.3.2 链路最大传输带宽确定

当节点发生数据交互时，节点状态一定属于兴态[11]，在下一刻发生时才会进行状态转移。假如处于当前周期T内，节点属于兴态，则对该节点来说，聚集的数据带宽值Bi应该满足下述条件

Bi=T×IT(V×ST)

(17)

式(18)中，T表示节点数据收发周期，V=(v1，v2，v3，…vn)代表节点在不同时间段内聚集信息时丢失的信息量，ST为矩阵的转秩。

假如在t+1时刻，节点和邻近节点传输信息总量为B，假如此节点传输信息总和高于聚集的信息带宽平均值时，该节点会出现状态转移现象，同时链路也会随之转移，判断转移的条件为

B>Bi

(18)

再结合式(16)可得，在经历t+1时刻后，表示节点i状态的向量Ri满足如下条件

Ri(n)=[S0，1，S1，2，S2，3，…，Sn，n+1]

(19)

如果节点i的状态描述为Ti，结合上述公式获得该节点的状态表达式为

Ti=Ri(n)ITIRi(n)T

(20)

公式中Ti为节点i在该时刻的兴态，将其设置为Si，当得到节点i的兴态后，对此兴态进行计算，就可以获得该节点在兴态时链路的最大信息传输带宽[12]。

2.3.3 链路优化

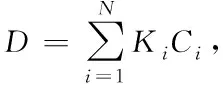
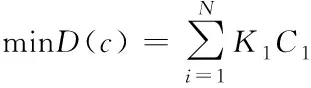
(21)

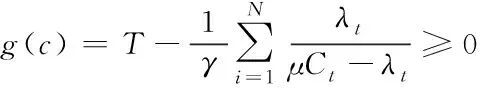
(22)

经过证明D(c)为凸函数，g(c)为凹函数，由于这两个函数在定义域中是持续可微的，C*在两个定义域内，因此D(c)与g(c)在C*处属于连续可微。C*满足K-T的要求，所以C*属于该线性规划问题的最优解。其表达式为

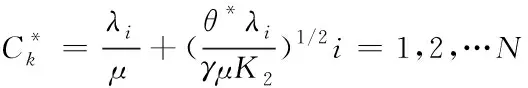
(23)

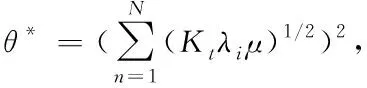
3 实验研究

为了验证基于聚类挖掘的移动通信网络链路优化设计的效果及可行性，设置实验，实验对象以一个公用数据移动通信网络为例。A设为中心点，B、C、D分别代表1、2、3级节点，将这三个节点与上一级节点互相连接，此时产生3条链路。

为使计算过程更加简便，设置3级节点的报文流相同，为1报文/s，因此整个通信网络的吞吐量为：γ=1×30×5×10=1500。每一级链路产生的报文流量记为：λ1=120、λ2=50、λ2=5。假如每条链路上的报文长度都相等，1/μ=1000。C*表示链路容量，D*为链路消耗，T*代表网络通信平均延时。为更直观看出本文方法优越性，下述对比图分别从移动网络通信中断概率、链路信噪比与传输功率方面进行对比描述。

从图1到图3可以看出，在用户数量增加的前提下，所提方法的中端概率比文献[1]方法和文献[2]方法小，且信噪比高，保证通信质量，在迭代次数增加时，传输功率有所降低，从而减少了对用户的干扰。使用本文方法与文献[1]方法和文献[2]方法进行优化对比实验，其结果如表1所示：

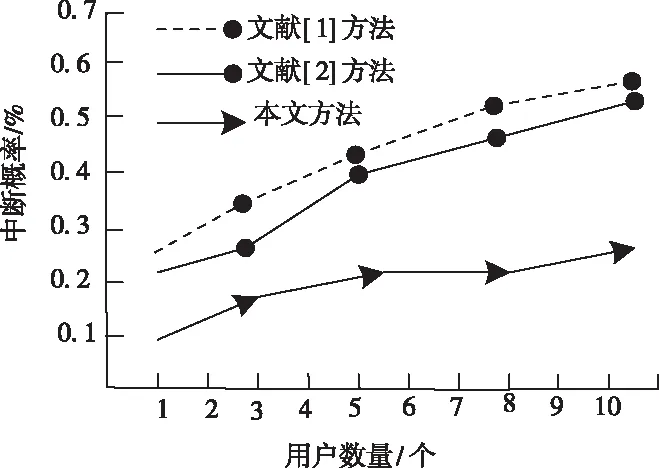
图1 不同方法传输中断概率对比图

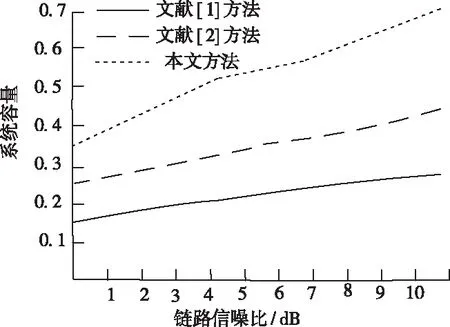
图2 不同方法链路信噪比对比图

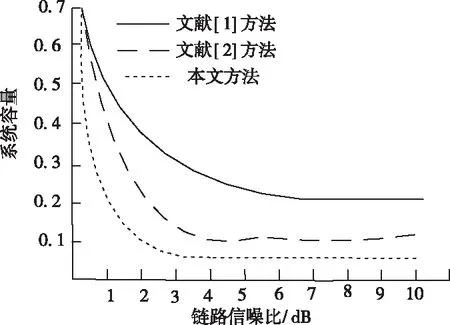
图3 不同方法传输功率对比图

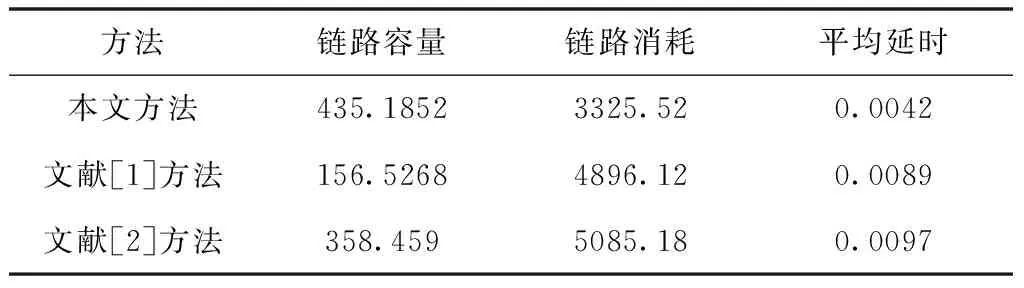
表1 不同优化方法仿真对比结果

根据表1可以看出，经过不同方法对通信链路进行优化后，所提方法的链路容量最大，链路消耗与传输平均延时均低于文献[1]、文献[2]方法。

4 结论

移动通信网络链路优化属于多目标优化问题，要想找到最佳解较为困难，因此本文提出基于聚类挖掘的移动通信网络链路优化设计。通过对聚类挖掘算法的分析，对失效链路进行估计，减少无用链路对整体网络结构的干扰；挖掘节点与邻近节点对链路优化的作用，并通过马尔科夫转移法构建通信链路矩阵，获取最佳解，完成链路优化。仿真表明聚类挖掘方法用于链路优化中性能良好，适用于不同环境下的链路容量优化。