与“因式分解”交朋友
文/江苏省无锡市西漳中学 陈兰馨
学习了整式的乘法之后,我知道了整式乘法就是由“乘”到“加”的过程,那反过来,由“加”到“乘”的过程是什么呢?学习完本章,我认识了一位新朋友——因式分解。
由“加”到“乘”的过程就是因式分解。它和整式乘法是互逆的过程,准确地说就是把一个多项式写成几个整式的积的形式,这样的过程叫作多项式的因式分解。注意,单项式是没有因式分解的哦。
因式分解还有好多解法,比如:提公因式法、公式法、分组分解法、十字相乘法等。下面,我们再来认识一下它的这些解法吧。
提公因式法:一般地,如果多项式的各项有公因式,我们可以把这个公因式提到括号外面,将多项式写成因式乘积的形式。
公式法:利用完全平方公式或平方差公式将多项式写成整式乘积的形式。
要想认识它们,就要充分地观察,发现它们的特征,这样就能够想到和识别出它们了。
例如,因式分解:4ab2-4a2b-b3。
我们先把这个多项式分为3个单项式:4ab2,-4a2b和-b3。仔细观察后发现,这三个单项式都有共同的成分b。这个b就是公因式。提取公因式b后,我们得到b(4ab-4a2-b2)。再观察,发现括号内为类似于完全平方公式的多项式,但是不完全一样。要使这个多项式变为标准的完全平方公式,就要提取负号。随后得到-b(4a2-4ab+b2),接着,利用完全平方公式,得到-b(2a-b)2。
公式法中,除了利用完全平方公式进行因式分解,还可以利用平方差公式进行因式分解。
例如,因式分解:x2y2-16。同学们可以动手做一做哦。
因式分解的第三种解法是分组分解法,即针对前两种解法无法直接解决的情况,通过分组的方式,从局部到整体,逐步分解。分解的方式一般分为“1+3”式或“2+2”式。
例如,因式分解:x2+2xy+y2-36。
这是一个含有4个单项式的多项式。我们观察前三项,会发现这是典型的完全平方公式。于是我们将原式部分分解为(x+y)2-36。有些小伙伴进行到这步,便止步不前了。但我们再将36看成62,把x+y看作一个整体,会出现什么呢?这不是平方差公式吗?于是,进一步分解,便可以得到(x+y+6)(x+y-6)。
再如,因式分解:x2-7x+6。
通过观察,我们会发现,这里没有公因式,也不具备乘法公式的特征,不能用提公因式法和公式法。我们再仔细观察,还会发现,-7x可以拆成-x和-6x,于是原式化为x2-x-6x+6。观察局部,前两项有公因式,后两项也有公因式,于是提公因式法就可以来帮忙了。局部分解,得到x(x-1)-6(x-1)。再提取一次公因式,就得到(x-1)(x-6)。
对比结果和原式,结合思考过程,我们可以发现:x2可以分解为两个x的积,6可以看成-1和-6的积,而-7x正好可以看成-x和-6x的和。有人把这个过程设计成“十字相乘”的样子,如图1。
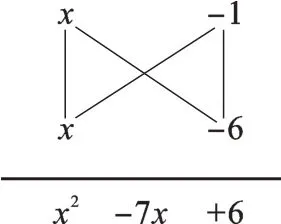
图1
这种“十字相乘”的方法,也是因式分解的第四种方法——十字相乘法。即十字左边相乘等于二次项,右边相乘等于常数项,交叉相乘再相加等于一次项。这其实就是乘法公式(x+a)(x+b)=x2+(a+b)x+ab的逆运算,通过分组分解来进行因式分解。
当然,因式分解的方法可不止这四种,还有其他方法,比如换元法、待定系数法、双十字相乘法,等等。有兴趣的小伙伴可以利用网络资源广泛结识这些好朋友。
教师点评
小作者用轻松的文笔为大家介绍了因式分解及其四种基本方法,不仅注重知识的学习,更关注知识运用的方法及背后的原理。这也启发我们,学习数学知识的时候,不仅要“知其然”,还要“知其所以然”,只有这样,我们才能学好数学,好学数学。

