改进Autogram及其在滚动轴承故障诊断中的应用

何勇，王红

（兰州交通大学 机电工程学院，兰州 730070）

滚动轴承作为机械传动系统的重要组成部件，尽早实现其故障特征的准确识别，可以有效避免因轴承失效而引发的重大安全事故。但由于轴承早期故障特征较为微弱，故障特征极易淹没在强背景噪声中，难以识别[1]。

为提取振动信号中的瞬态冲击特征，Dwyer[2]对峭度进行了定义。随后，Antoni[3-4]对其进行了系统定义，并基于短时傅里叶变换提出了谱峭度计算方法，但该方法计算时间长、效率低。为提高计算效率，Antoni[5]又提出了基于1/3—二叉树滤波结构的快速谱峭度（Fast kurtogram, FK）计算方法，该方法大幅提高了计算效率。快速谱峭度虽然在滚动轴承故障诊断中取得了较好的应用效果，但峭度着重关注瞬态冲击特征强弱，未能考虑周期性冲击特征[6-7]。同时，在信噪比较低时，峭度易受噪声脉冲干扰，进而导致最优频带的带宽及中心频率识别效果不佳、诊断错误[8-9]。

为克服上述不足，部分学者针对最优解调频带的确定方法进行了详细研究。Wang[10]以稀疏值最大化为优化目标，采用遗传算法对复Molert小波进行优化，以实现其自适应带通滤波，即Sparsogram方法。Barszcz等[8]将窄带带宽固定，以窄带包络谱峭度最大值为寻优目标，依据轴承理论故障频率的先验知识对最优中心频率进行搜索，即Protrugram。该方法的故障特征提取效果虽然优于FK，但在特征提取时需要反复试算。Antoni[11]通过引入谱负熵的概念，提出了同时考虑信号冲击特性和循环特性的Infogram。Moshrefzadeh等[12]针对信号中的周期性冲击成分提出Autogram方法，该方法对滤波后信号平方包络的自相关求峭度，从而进行故障诊断。与最佳频带确定方法相比，信号的频谱分割方法也对故障特征提取至关重要。因此，部分学者针对频谱分割方法亦进行了详细研究。胥永刚针对Infogram中的频带划分方法进行了改进，提出了基于经验小波变换（Empirical wavelet transform, EWT）的频域扫描滤波精细谱负熵诊断方法[13]。Autogram以最大重叠离散小波包变换（MODWPT）为基础，采用二叉树结构对频谱进行划分。郑近德针对该方法在频带划分时边界位置不能与信号实际特征相适应的不足，提出了基于顺序统计滤波（Order statistic filtering,OSF）的自适应频带分割方法[14]。但MODWPT和OSF在划分频带时均需预设分解层数（或频带个数），从而使得诊断效果易受人为因素影响。

为进一步降低预设参数对故障特征提取准确性的影响，本文提出一种以平均包络熵为优化目标的MODWPT最佳分解层数确定方法。并在此基础上以滤波后信号平方包络自相关峭度最大值选取最优频带的中心频率及带宽，从而实现Autogram对滚动轴承故障的自适应诊断。最后，通过人为预设故障试验及全寿命加速试验两组实测信号分析，验证了本文方法有效性。

1 改进 Autogram 算法

为有效提取强高斯背景噪声和非高斯背景噪声下故障特征频带的中心频率及带宽，Moshrefzadeh[12]提出了一种新的最佳频带寻优目标—平方包络自相关峭度，即Autogram。

1.1 自适应最大重叠离散小波包变换

Autogram采用最大重叠离散小波包变换（MODWPT）对频带进行划分，该方法是对离散小波包变换（Discrete wavelet packet transform, DWPT）的改进。MODWPT通过向第j层分解过程中的滤波器插入2j−1−1个0值，来避免DWPT分解过程中降2采样导致的信号采样点损失。最大重叠离散小波变换的尺度滤波器和小波滤波器与离散小波变换的尺度滤波器gl和小波滤波器hl有如下关系：

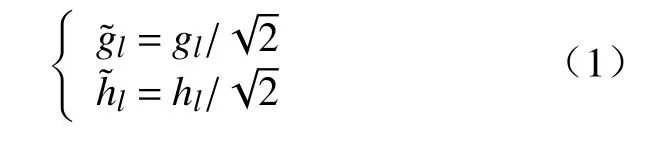
且满足：

为避免DWPT中降2采样导致的采样点减少，在尺度j下，在和中插入2j−1−1个0值，即：

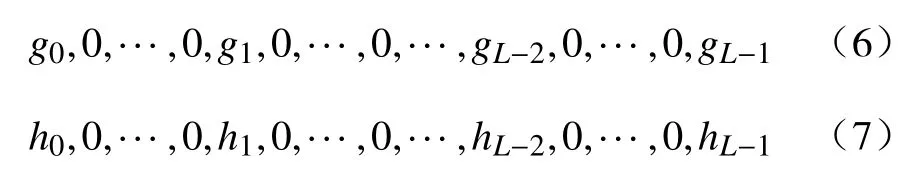
此时，根据Mallat算法可计算得到尺度j下最大重叠离散小波变换（Maximum overlap discrete wavelet transform, MODWT）的和为：

MODWPT是对MODWT高频段的进一步分解，可以提高信号频率的分辨率。MODWPT的分解系数可表示为其中j为分解层数，n为一个随分解层数变化的频率索引。则计算得到Wj,n,t为

其中，若nmod4=0或3，则若nmod4=1或 2，则

为了避免MODWPT分解时人为预设分解层数对诊断效果造成的干扰，本节构建了自适应MODWPT分解方法。该方法分别对不同分解层数下每个节点的包络熵进行计算，进而得到不同分解层数的平均包络熵 MEE（Mean envelope entropy），表达式为

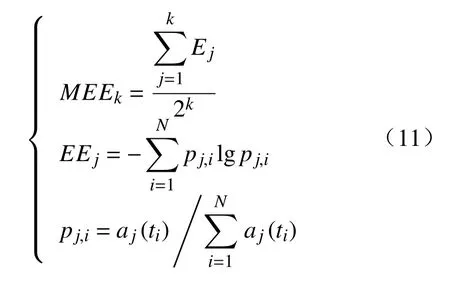
式中：k为分解层数；j为该层数下各节点X(ti)的序号为信号长度；aj(ti)为节点X(ti)序号为j的包络信号。通过对不同分解层数MEE的计算，建立了以最小平均包络熵为准则的MODWPT最佳分解层数确定方法。

1.2 最佳解调频带确定方法

根据1.1节中确定的最佳分解层数，分别计算信号分解后每个节点平方包络的无偏自相关（Unbiased autocorrelation，AC），表达式为

式中：X为分解信号的平方包络； τ =q/fs为时移参数（q=0,1,2,3,···,N−1），fs为采样频率。通过对无偏自相关估计的计算能够有效抑制与故障特征无关的噪声成分。此外，由于滤波信号的第一系数受滤波器瞬态的影响，因此需要将其剔除。与此同时，为量化频带内信号的脉冲成份，对传统峭度计算方法进行了修正，并将与修正峭度最大值相对应的节点用于进一步的分析。修正后的峭度为

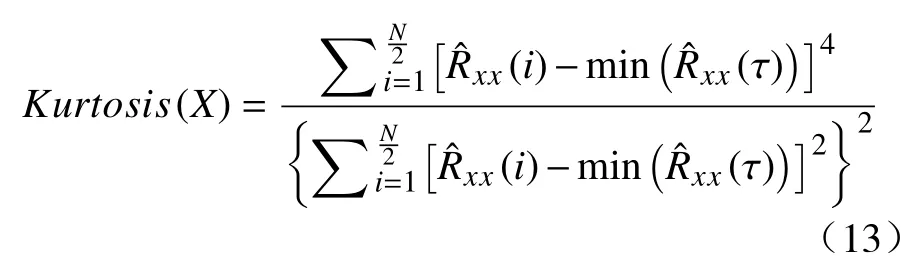
1.3 改进Autogram诊断流程

改进Autogram的诊断流程如图1所示。首先，对滚动轴承故障信号进行采样，利用MODWPT对信号进行分解。其次，计算不同分解层数的平均包络熵，进而确定最佳分解层数。再次，分别计算每个节点平方包络的自相关函数及其峭度，并选择与峭度最大值对应的节点进行频谱分析。最后，通过包络谱分析完成对滚动轴承的故障诊断。

图1 改进 Autogram 诊断流程

2 案例分析

2.1 人为预设故障分析

采用美国凯斯西储大学滚动轴承数据集对本文方法进行验证，试验轴承型号为6205RS JEM SKF，故障尺寸 0.021′′，电机负载 2.205 kW，采样频率fs=12 000 Hz，轴承试验转速为 1 730 r/min（转频fr=28.83 Hz），根据轴承故障特征频率理论计算公式可以得到轴承内圈故障频率fi=156.1 Hz。由于人为植入故障试验信号含噪量较小，本节参照文献[15]中的研究方法，在原信号中加入了信噪比为−3 dB的高斯白噪声，使得信号复杂程度更高，加噪后信号的时域波形如图2a）所示，包络谱如图2b）所示。由图2可知，加噪后信号的包络谱无法识别出轴承内圈故障频率，采用IAutogram方法首先对MODWPT最佳分解层数进行确定，不同分解层数的MEE如表1所示。

表1 轴承内圈信号不同分解层数 MEE

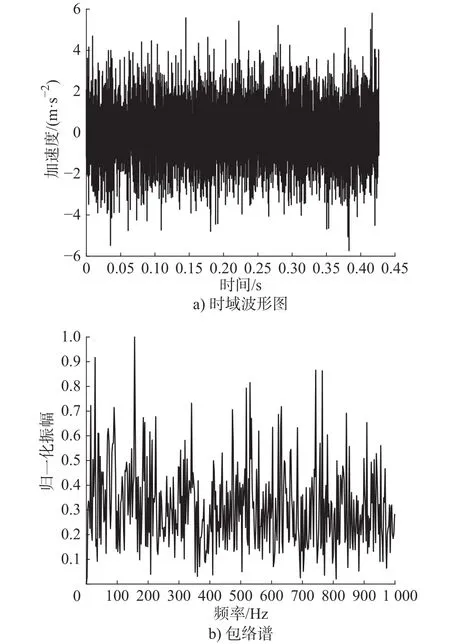
图2 内圈故障信号

由表1可知，最佳分解层数为3层，IAutogram峭度图如图3所示，选取自相关峭度值最大的节点作为最优频带，提取故障特征频率如图4所示。从最佳节点归一化包络谱中已经可以明显观察到轴承内圈故障频率及转频，验证了本文方法可以自适应地现故障特征与背景噪声的分离。

图3 IAutogram 峭度图

图4 最佳节点包络谱（k=3）

若人为将分解层数设置为4，计算得到最佳节点自相关峭度值如图5所示，该节点的包络谱如图6所示。对比图3和图5可知，虽然最佳节点的自相关峭度值有所增加，最佳节点的包络谱中最大峰值处亦与轴承内圈故障频率相对应，但被其他谱线干扰严重，无法进行有效故障诊断，易出现轴承故障误诊。上述分析表明，仅通过自相关峭度值来进行滚动轴承故障诊断未能取得较好效果，需要合理确定MODWPT的分解层数。

图5 Autogram 图

图6 最佳节点包络谱（k=4）

2.2 全寿命试验故障分析

全寿命试验分析采用NSFI/UCR智能维护系统中的全寿命周期加速试验数据集[16]。该试验中轴承转速 2000 r/min，采样间隔为 10 min，共记录 9840 min，采样频率为 20 kHz，每次采集 20480 个点，试验轴承和传感器的安装位置如图7所示。

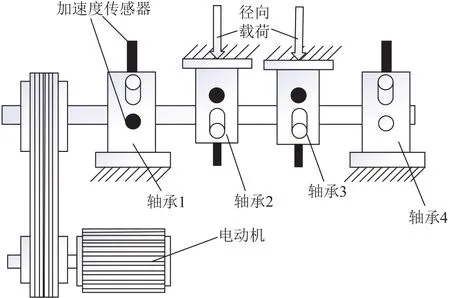
图7 轴承和传感器的安装位置[10]

试验结束后，发现1号轴承外圈出现损伤，根据轴承结构参数，计算得到轴承外圈理论故障频率为f0=236.4 Hz。参考文献[16]中的研究成果，本节以3800 min时采集得到的信号进行分析。信号的时域波形及包络谱如图8所示。

从图8中原始信号的时域波形中没有发现较为规律的周期脉冲成分，其包络谱中亦没有发现与外圈理论故障频率相对应的较大峰值。采用IAutogram方法首先对MODWPT的最佳分解层数进行确定，不同分解层数的MEE如表2所示。

表2 轴承外圈信号不同分解层数 MEE

由表2可知，最佳分解层数为2层， IAutogram峭度图如图9所示，选取自相关峭度值最大节点作为最优频带，其包络谱如图10所示。

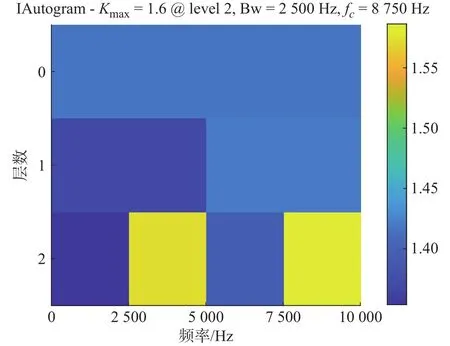
图9 IAutogram 峭度图

图10 最佳节点包络谱（k=2）

从最佳节点归一化包络谱中已可以明显观察到轴承内圈故障频率及其二倍频。文献[16]中提出了一种基于自相关分析（AutoCorrelation analysis）和最大相关峭度解卷积（Maximum Correlated Kurtosis Deconvolution, MCKD）的滚动轴承故障诊断方法，并将其定义为AC-MCKD。相比于文献[16]中的诊断方法，本文可以提前1 810 min发现轴承故障，验证了本文方法可以尽早的实现滚动轴承的故障特征提取，这对于安全性要求较高的行业来说，可以更大程度避免因轴承失效而导致的重大事故发生。

若将分解层数人为设置为3，计算得到最佳节点自相关峭度值如图11所示，该节点的包络谱如图12所示。对比图9和图11可知，虽然最佳节点的自相关峭度值有所增加，但从最佳节点的包络谱中无法找到轴承内圈故障频率，这也验证了本文改进的MODWPT最佳分解层数确定方法对Autogram诊断效果至关重要。

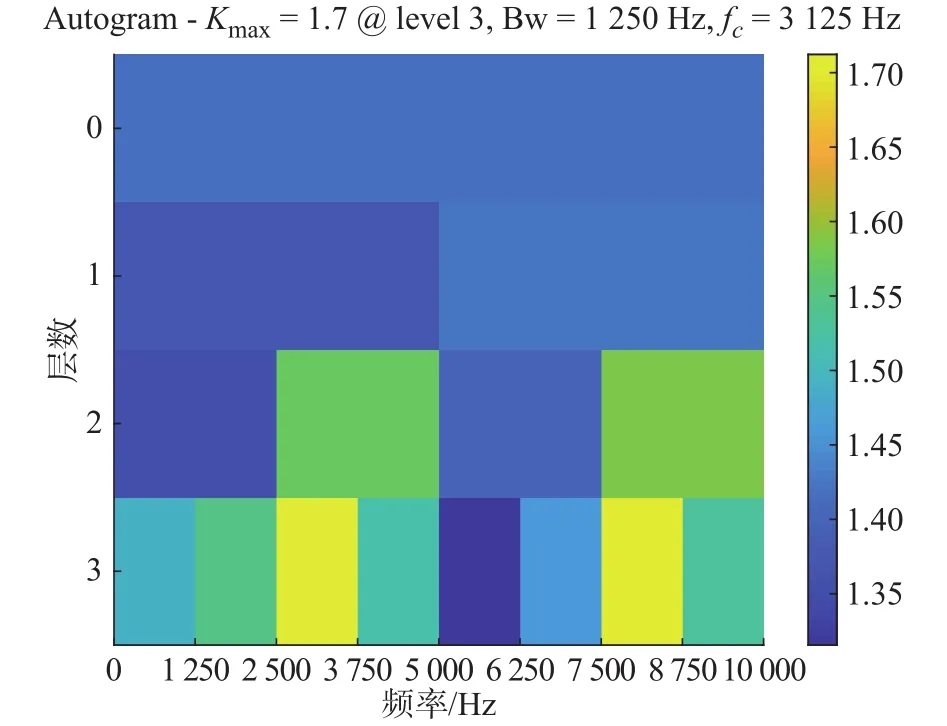
图11 Autogram 峭度图

图12 最佳节点包络谱（k=3）

3 结论

本文针对Autogram最优频带识别准确性易受MODWPT分解层数影响的不足，提出了一种基于平均包络熵的MODWPT最佳分解层数确定方法。为验证本文方法有效性，分别采用人为预设故障信号及全寿命试验信号进行分析。研究结果表明：

1）采用MEE构建的自适应最佳分解层数确定方法可以有效避免过分解或欠分解造成的降噪效果不佳。

2）通过与AC-MCKD方法的对比分析表明，该方法能够更早识别到周期性冲击特征，改进的Autogram可以自适应的实现滚动轴承故障诊断。