仅发射分集的MIMO雷达的高精度DOA估计算法

陈建明，焦 爽，陈光辉

(1. 华北水利水电大学电力学院，河南 郑州 450046；2. 重庆大学微电子与通信工程学院，重庆 400044)

1 引言

仅发射分集的多输入多输出(Multiple Input Multiple Output， MIMO)雷达采用多个天线发送波形并接收来自多个目标的反射信号[1]，在反隐身、反电子对抗与干扰等方面具有独特的优势。为了先敌发现和先敌出击，保证自身生存能力，良好的到达方向 (Direction of Arrival，DOA) 估计性能成为MIMO雷达探测目标信息的重要一环[2]。DOA估计方法可以分为：传统方法、子空间分解方法和压缩感知方法[3]。其中子空间分解方法中的多重信号分类(Multiple Signal Classification， MUSIC) 算法因其具有较高的DOA估计精度而被广泛的应用。

MUSIC算法将传感器阵列接收信源的线性空间分解为信号和噪声子空间，利用信号和噪声子空间之间的正交关系，扫描维度较低的噪声子空间，得到一个空间谱，其中空间谱谱峰所对应的角度即为信源的DOA。目前，MUSIC算法广泛应用在无线通信、导航、天文检测等众多领域[4]，具有高精度、高分辨率的优点，但却具有特征值分解计算量大，在低信噪比下DOA估计精度严重降低等缺点[6]。

文献[7]指出，一维MUSIC算法花费在估计协方差矩阵的时间占总时间21%，特征值分解占总时间61%，一维谱峰搜索占总时间18%，由此可见，MUSIC算法中特征值分解的计算量较大，占用计算总时间最多。为解决该问题，1995年，Marcos等提出了传播算子方法和正交传播算子方法[8]。这类算法引入线性运算代替协方差矩阵的特征值分解，有效的降低了算法的计算复杂度。但如何在低信噪比下有效的提高DOA估计精度依旧是当前的研究重点。因此，本文基于线性运算以及空间谱函数在DOA处是断点且趋近于较大值，而求导可以使断点处的峰值更加明显的物理性质提出一种改进的MUSIC算法。此方法不但有效的降低了计算复杂度，而且也有效的提高了在低SNR下DOA的估计精度。

2 仅发射分集双基地MIMO雷达信道模型

如图1所示的双基地MIMO雷达信道模型中， 目标数为K，发射阵列和接收阵列的阵元间距、阵元个数、方向矩阵分别为dt、Mt、At(θ)和dr、Mr、Ar(θ)。其中At(θ)和Ar(θ)被定义为

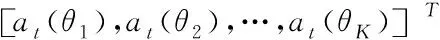
(1)

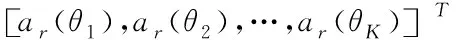
(2)

其中

(3)

(4)

其中，λc=c/fc为中心频率为fc的窄带信号的波长，c为信源传播速度。

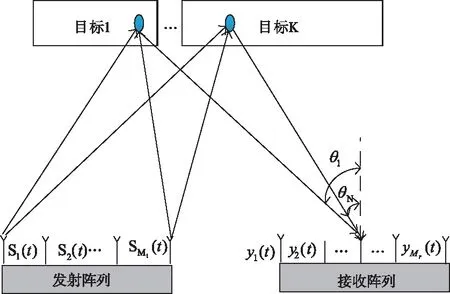
图1 双基地MIMO雷达信道模型

假设目标是由多个分布在一维区域的小散射体组成，并采用仅发射分集的MIMO雷达模型进行考虑，因此，目标具有K个独立的各向同性散射体，每个散射体被建模为零均值、单位方差、独立同分布的圆对称复高斯随机变量[9]。因此，目标的反射可以表示为对角阵，即

(5)

其中，第mth个发射元发射的信号时独立散射体的响应向量为

(6)

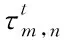
(7)

Ht=[g1，g2，…，gm，…，gMt]∈CK×Mt

(8)

Hr=[k1，k2，…，ki，…，kK]∈CMr×K

(9)

则MIMO雷达信道统计矩阵为

H=HrλHt∈CMr×Mt

(10)

要使不同发射天线阵元发出的信号从不同方向照射到目标，则发射方向矩阵的列向量应满足正交条件[10]，即

〈gm，gl〉=0，m≠l，m，l=1，…，Mt

(11)

由式(11)可知，任意两个不等的gm均满足正交关系，为了降低模型的复杂性，将其简单的考虑为相邻发射单元引入的响应向量之间的正交性[11]，即

〈gm，gm+1〉=0，m=1，…，Mt

(12)

假设目标散射体是平行于发射阵列和接收阵列的均匀阵列，则第mth个发射元发射时散射体的响应向量被表示为

(13)

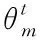
(14)

N→∞，化简得

(15)

其中，rt为发射阵列与目标的距离。假设接收阵列为dr=λc/2的均匀线性阵列且无法分辨目标散射体的回波信号，接收方向矩阵可以表示为

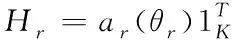
(16)

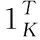
Hr=ar(θr)αT

(17)

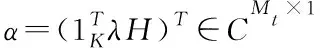
式(17)为双基地MIMO雷达接收阵元无角度扩展的极端情况[11]。由此可得出如图2所示的仅发射分集双基地MIMO雷达信道模型。其中接收信号向量可表示为

y(n)=Hrs(n)+v(n)

(18)

其中，s(n)为窄带发射信号，v(n)为噪声向量。

图2 仅发射分集的MIMO雷达信道模型

3 改进的MUSIC算法原理

在加性高斯白噪声下，仅发射分集的MIMO雷达接收阵列的空间协方差矩阵可以表示为

(19)

其中，矩阵P的第(m，l)个元素为

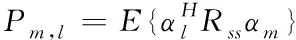
(20)

其中，Rss为发射信号s(n)的协方差矩阵，即

Rss=E{s(n)sH(n)}

(21)

假设发射器信号为正交信号，则Rss可表示为

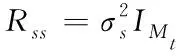
(22)

假设目标衰落满足独立条件，即

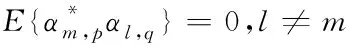
(23)

(24)

易证

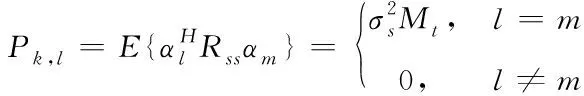
(25)

(26)

将式(26)带入式(19)，可得接收阵列的协方差矩阵为

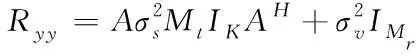
(27)

改进的MUSIC算法引入线性运算代替矩阵的特征值分解，降低计算量，得到空间谱。最后对空间谱函数求一阶导数。具体原理如下：

由于信源统计独立，可以定义一个传播算子矩阵P把协方差矩阵Ryy线性分割为[12-14]

(28)

其中R1是K×Mr维，R2是(Mr-K)×Mr维，R1和R2满足下式

R2=PHR1

(29)

考虑噪声影响，一般求

ξ(P)=‖R2-PHR1‖F

(30)

的极小值，得到P的估计值，其中‖·‖F表示F-范数[12]。而可表示为

=(R1RH1)-1R1RH2

(31)

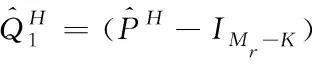
(32)

(33)

由此可得

Q0A=0

(34)

由式(34)定义新的空间谱

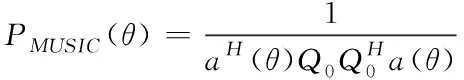
(35)

定义PMUSIC(θ)的一阶导数d(θ)为

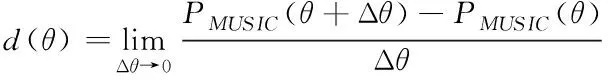
(36)

为方便计算，将步长Δθ取较小的值，用Φ(θ)代替d(θ)，则Φ(θ)为

(37)

假设θ0为谱峰函数的峰值点，也即是信源的DOA。则PMUSIC(θ0)趋近较大值，PMUSIC(θ0+Δθ)和PMUSIC(θ0-Δθ)远小于PMUSIC(θ0)，因此Φ(θ0-Δθ)趋近于正较大值，Φ(θ0)趋近于负较大值。其中Φ(θ0-Δθ)与Φ(θ0)的具体表达式为

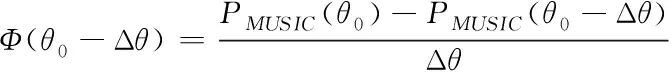
(38)

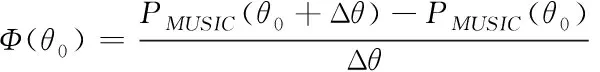
(39)

因此，可以根据Φ(θ)函数是否先正较大值突变，后负较大值突变判断信源的DOA。同理，如果PMUSIC(θ)函数在极小值处也是突变函数，可以根据先负较大值，后正较大值突变来判断极小值点。但由PMUSIC(θ)函数的物理含义(扫描向量a(θ)到噪声子空间的欧几里德距离的倒数)和式(34)可知，PMUSIC(θ)只会在信源的DOA上产生断点。因此，可以根据Φ(θ)函数突变来判断信源的DOA：Φ(θ) 函数若有先极大值后极小值的突变，则处于极大值与极小值之间的零点所对应的角度即为信源的DOA。

设θ1、θ2分别是两个信源的DOA，理论分析改进的MUSIC算法是否提高了DOA的估计精度。定义MUSIC算法的估计精度为

(40)

改进的MUSIC算法的估计精度为

(41)

把式(37)带入式(41)得

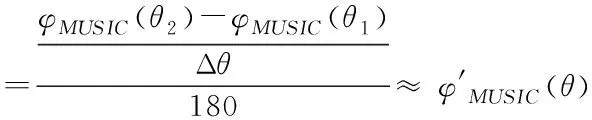
(42)

由式(42)可知，改进的MUSIC算法的估计精度近似于MUSIC算法估计精度的导数，且由空间谱函数的物理性质以及式(34)和式(37)可知，改进的MUSIC算减小了信源在DOA处的空间相关性，使断点处的谱峰更加明显，提高了DOA的估计精度。

4 改进的MUSIC算法

1)根据仅发射分集双基地MIMO雷达信道模型和式(27)计算协方差矩阵Ryy；

2)根据式(28)将Ryy线性分割；

3)根据式(29)求传播算子矩阵P，然后根据式(31)计算传播算子矩阵P的近似值；

4)根据式(32)和式(33)求矩阵Q0；

5)根据式(35)定义空间谱函数PMUSIC(θ)；

6)根据式(37) 定义PMUSIC(θ)的近似一阶导数Φ(θ)，其中Φ(θ)函数的突变处即为信源的DOA。

5 仿真分析

5.1 信源角度差仿真分析

阵元个数Mr=10；阵元间距dr=λc/2；采样快拍数L=100；信噪比SNR=5dB，步长Δθ=0.01，噪声为高斯白噪声，目标信源是2个非相关的远场窄带信号，DOA分别是(20°，21°)、(30°，33°)和(40°，45°)，信源角度差分别为1°、3°、5°。分别用MUSIC算法和改进的MUSIC算法对其进行仿真，结果如图3和图4所示。

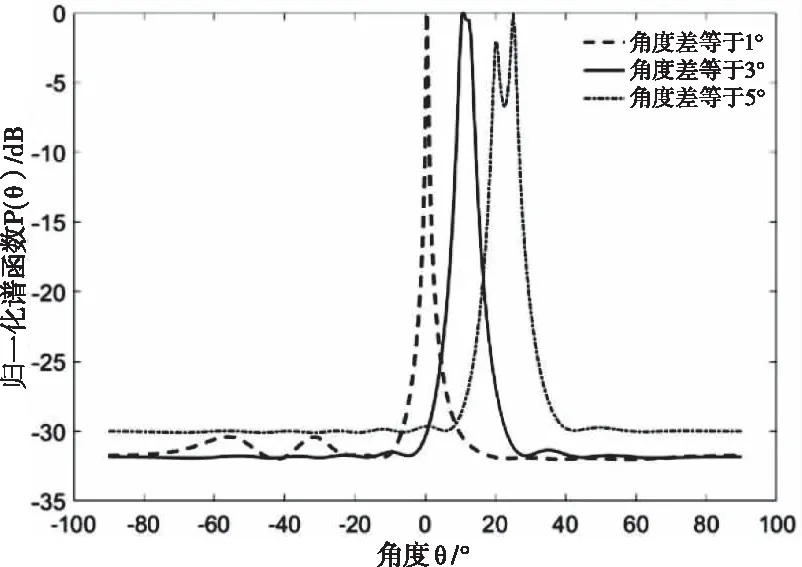
图3 不同角度差下的MUSIC算法仿真结果图

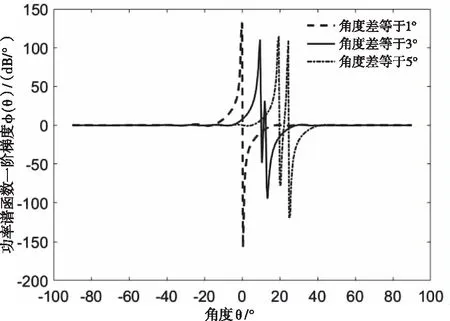
图4 不同角度差下本文的算法仿真结果图

由图3可知，MUSIC算法在角度差等于1°和3°时完全失效，只能估计出一个目标信源的DOA，在角度差等于5°时，可以估计出两个目标信源的DOA，但谱峰不明显。由图4知，相同的条件下，当角度差为1°时，改进的MUSIC算法也只能检测出一个谱峰，但对于角度差为3°和5°时，可以有效的检测出2个谱峰，且谱峰明显。原因是当信源DOA相距较近时，信源的空间性较强，而改进的MUSIC算法在MUSIC算法的基础上先进性线性运算，后对谱峰求一阶导数，减小了信源在DOA处的相关性，提高了DOA的估计精度。所以，与MUSIC算法相比，改进的MUSIC算法可以有效的提高了仅发射分集MIMO雷达的DOA估计精度。

5.2 信噪比分析

定义DOA的估计均方根误差(Root Mean Square Error，RMSE)为：

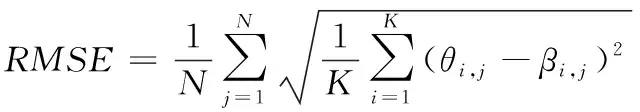
(43)

其中，N为Monte Carlo实验次数，K为目标信号源的个数，θi，j为第j次Monte Carlo实验中βi，j的估计值。仿真了RMSE随SNR变化的性能，SNR变化的范围为-10dB到10dB，步进为2dB，采样快拍数L=1024。仿真结果如图5、图6所示。

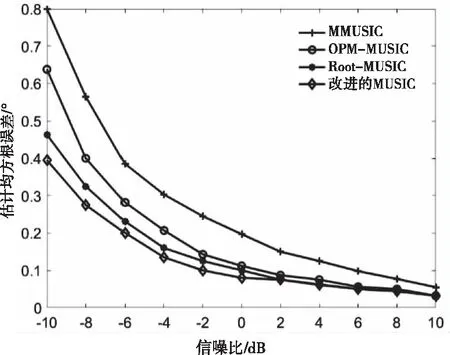
图5 4种算法的RMSE随SNR变化曲线图

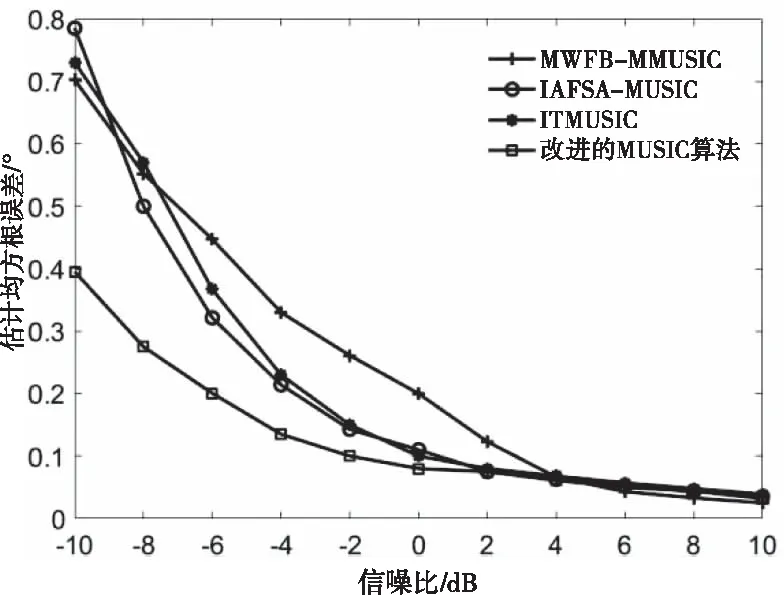
图6 4种算法的RMSE随SNR变化曲线图

由图5可知，随着SNR的增加，算法的估计精度也增加，RMSE逐渐减小，最后趋近于0。在信源角度差等于10°时，相同条件下，改进的MUSIC算法的RMSE值小于图中几种典型的MUSIC改进算法，并在低信噪比时更加明显。由图6可知，与文献[15]的MWFB-MUSIC算法、文献[16]的IAFSA-MUSIC算法和文献[17]的ITMUSIC算法相比，改进的MUSIC算法在低信噪比下RMSE值更低。因为在低信噪下，信号的空间相关性强；在高信噪比时，信号空间相关性弱，而本文算法引入线性运算代替特征值分解，并通过对空间谱函数求一阶导数构造一个新的空间谱函数，有效的降低了DOA处的空间相关性，提高了仅发射分集MIMO雷达的DOA估计精度。

5.3 复杂度分析

MUSIC 算法的计算量主要包括构造Mr×Mr维的协方差矩阵，协方差矩阵特征值分解和一维谱峰搜索。而改进的MUSIC算法的计算量主要包括构造Mr×Mr维的协方差矩阵，协方差矩阵线性处理和一维谱峰搜索。具体的计算量如表1和表2所示。其中Mr为阵元数，K为目标信源个数，L为采样快拍数，Δθ为角度扫描间隔。

表1 MUSIC算法的计算量分析表

表2 改进的MUSIC算法的计算量分析表

对比表1和表2知，K、L和Δθ一定，MUSIC算法的计算量大约是改进的MUSIC算法M倍。因为改进的MUSIC算法引入线性运算代替特征值分解，降低了计算量；Mr、K和Δθ一定，MUSIC算法和改进的MUSIC算法的计算量都随L线性增加，但因为K

6 结论

本文基于线性运算、空间谱函数的物理性质，提出了一种改进的MUSIC算法。其可以有效的提高低SNR下仅发射分集的MIMO雷达DOA的估计精度。同时，该算法也可以有效的降低了计算量。