考虑水库来用水过程关联性的多维随机动态规划算法

郭爱军，畅建霞※，王义民，黄 强，吴 彬，张 春

（1. 西安理工大学西北旱区生态水利国家重点实验室，西安 710048；2. 华能西藏雅鲁藏布江水电开发投资有限公司，拉萨 850000）

0 引 言

水库是实现水资源时空均衡分配、解决水资源供需矛盾的关键工程措施。水库兴利调度作为水库控制运用的核心非工程措施，旨在根据水库开发任务和综合利用要求，根据来、用水过程制定水库蓄泄规则，最大限度满足各个用水部门用水需求，实现水资源供给过程与需求过程的高度匹配。根据对水库入库径流的处理方式，水库调度可分为确定性调度与随机调度，确定性调度认为入库径流是已知和确定的，但往往受限于历史有限的实测资料，难以全面反映径流变化过程；随机调度将径流作为具有一定统计特性的随机变量或随机过程处理，能够更好地体现径流序列的不确定性。

作为求解水库中长期随机优化调度模型的算法之一，随机动态规划算法自提出之后在流域水资源管理和水库调度中被广泛采用。黄强分别采用确定性、独立随机性、简单马氏性过程与混合性过程描述了径流过程，并改进了有径流预报下的随机动态规划求解策略，应用于以发电量最大为目标的水库优化调度模型中；周惠成等以二滩水电站为例，提出了有、无预报与随机过程相结合的径流描述方法，建立了发电优化调度模型，制定了电站优化调度图；卢迪等采用径流预报概率修正先验概率来描述径流的不确定性，建立了贝叶斯随机动态规划模型，分析了有跨流域引水的碧流河水库调度策略；崔远来等考虑降雨过程的随机性，建立了解稻田高效节水优化灌溉制度的随机动态规划模型；Nop等基于降雨过程的马尔可夫性，将随机动态规划算法应用于雨水收集系统中的水资源管理问题；Cassagnole等分析了径流预报质量的不同对水库电站效益的影响；Zhou等采用离散时间马尔可夫链描述水库入库径流过程，采用随机动态规划算法以及机会约束模型推求了溪洛渡水电站的中期发电运用计划。

如上所述，随机动态规划算法的核心之一是入库径流或降雨等水文过程的随机性的描述。农业灌溉用水是中国的主要用水部门，其需水量和需水过程受气候条件的影响显著，具有很强的随机性；并且，农业灌溉需水与入库天然径流同受降雨、气温等气象因素影响，在流域气象条件的相似性背景下，农业灌溉需水与入库天然径流呈一定的负相关性，且流域范围越小，负相关性越为显著。如何在水库随机优化调度中同时考虑需水与径流二维过程的随机性与关联性，以往研究对此考虑不足。有限的研究也主要是从径流的随机性角度出发，忽略了农业灌溉需水的随机性及其与径流之间的关联性，使得随机规划理论模型与现实水文过程之间的匹配性不足。本研究结合马尔可夫过程与Copula函数描述需水与径流二维过程的随机性与关联性，基于随机动态规划理论，提出考虑水库来、需水过程关联性与随机性的水库优化调度算法，并进行相关案例分析。该算法对于农业水土资源随机优化配置等领域的优化决策求解具有支撑作用。

1 水库来、用水多维过程关联性与随机性

1.1 一维过程随机性与关联性

随机动态规划是确定性动态规划与随机过程二者的结合。相较于确定性动态规划，随机动态规划的复杂性主要体现在随机过程的处理方面，即固定阶段（或时段）随机变量的随机性描述与阶段（或时段）之间随机变量的关联性；求解步骤与思路方面，随机动态规划与确定性动态规划一致，随机动态规划具体求解步骤可参考文献[8, 22]。

径流或需水一维随机过程的描述可从固定时段下变量的随机性与相邻时段间变量的关联性两个方面展开。此处，固定时段指以水库调度时间尺度为标准，如开展以月为时间尺度的中长期水库调度时，固定时段则为一月、二月、三月、……、十二月，重点关注各个固定时段下变量的随机性，如长系列一月径流的随机性等；相邻时段则以固定时段相邻为具体情形，如一月与二月相邻时段、二月与三月相邻时段等，本文重点关注相邻时段间随机变量关联性，采用状态转移概率矩阵来表征两两随机变量不同状态间的关联特性。

1）固定时段下随机性描述

径流与需水的随机性采用传统单变量概率分布函数描述。本次研究选择水文领域应用较广的伽马分布（Gam）、对数正态分布（Logn）、广义极值分布（Gev）、威布尔分布（Weibull）、正态分布（Norm）、指数分布（Exp）作为拟合固定时段下径流或需水随机变量的备选概率分布类型，采用极大似然法（Maximum Likelihood Estimate，MLE）估计不同概率分布函数参数，选用王义民等提出的基于多评价准则的综合指数法选择适宜概率分布函数。基于多评价准则的综合指数包括修正的赤池信息准则（Corrected Akaike’s Information Criterion）、离差绝对值和最小准则、均方根误差和相对离差平方和最小准则，利用不同准则所侧重的评价方向，综合优选适宜概率分布函数。

2）相邻时段间过程关联性描述

随机变量时段之间的关联性影响随机过程描述的方式。若相邻时段之间随机变量相互独立，则可判断该随机过程为独立过程，随机变量不同状态间的转移概率为0；若相邻时段之间的随机变量相关性较强，难以忽视，即对该随机过程的演变而言，在已知目前状态的条件下与以往的状态无关，该特性称为马尔可夫性，若随机过程转移至下一阶段某一状态时只与系统当前状态相关，称之为一阶马尔可夫过程或简单马尔可夫过程，若与其前面连续的个状态相关，与个状态以前的状态无关，称之为阶马尔可夫过程或复杂马尔科夫过程。径流与需水过程是典型的随机过程，若相邻时段之间或当前时段与前面连续的个时段的变量具有显著相关性，则可认为径流与需水过程是马尔可夫过程；由于多时段相关的径流与需水过程描述较为复杂，实际应用中也较少，因此本次研究重点关注相邻时段间随机变量的状态转移过程，即未来时段径流与需水状态的演变只与当前时段状态有关。具体做法为，根据时段之间变量的相关性是否显著，采用简单马尔科夫过程（时段间变量相关性显著）或独立过程（时段之间变量相关性不显著）描述径流、需水过程。径流、需水过程描述的关键是推求相邻时段随机变量不同状态的条件转移概率P。以相邻时段径流不同状态转移概率{Q()|Q()}计算为例，其公式如下：

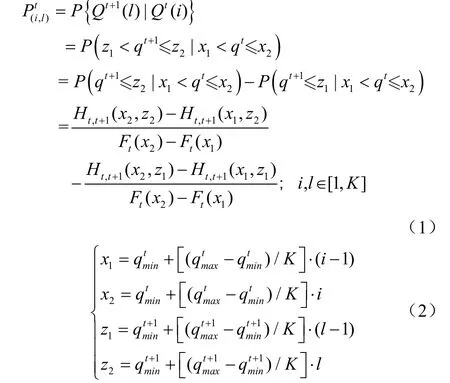
式中为固定时段随机变量离散总数；、为时段随机变量第个状态与时段+1随机变量第个状态；H(·)为时段与时段+1变量联合分布函数；F(·)为时段变量概率分布函数；q、q为时段径流的最小值与最大值，m/s；、分别为时段径流在状态下的下限与上限；、分别为时段+1径流在状态下的下限与上限。

变量状态数量为时，全部状态转移及相应的转移概率便有种，则转移概率矩阵P为

此处，转移概率矩阵满足以下条件：

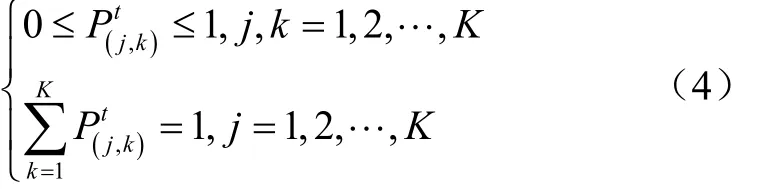
式中表示随机变量的第个离散状态。

本次研究选用在水文水资源领域、经济领域应用广泛的Copula函数表征时段与时段+1变量联合分布函数H(·)。Copula函数是一种描述多变量相关性的连接函数，其优势在于可灵活选用边缘分布函数且联合分布函数构造简单、灵活，易于求解。需要注意的是，Copula函数仅用于拟合变量间相关性显著的时段，若变量间相关性不显著，则认为变量彼此独立。

Copula函数(·)表达形式如下：

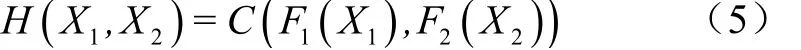
式中(·)为边缘概率分布函数，()、()分别为变量、的边缘概率分布函数。Copula函数发展至今，已有多种类型（如椭圆型、Archimedean型、二次型等）。其中，Archimedean型Copula函数是水文水资源领域应用较为广泛的类型之一。本次研究选择Archimedean型Copula函数中的Clayton Copula、Gumbel-Hougaard Copula、Frank Copula三种函数为备选类型，采用极大似然函数估计Copula函数的参数，选用Cramer-von Mises统计量进行拟合优度检验，进而选择最优的Copula函数类型。

Copula函数的参数可用于量化变量之间关联程度，以Clayton Copula函数为例，参数→0时，表明变量与趋于独立，参数→+∞时，表明变量与趋于完全相关，参数在（0，+∞）内变化，与肯德尔秩相关系数的关系为=/(+2)。

1.2 径流与需水多维过程关联性与随机性

与一维随机过程不同的，多维随机过程考虑特定时段下多维变量之间的独立关系或相关关系；相邻时段间，考虑多维变量时段第个状态内部关联性的基础上向时段+1第个状态转移的过程，与1.1节单一变量的状态转移形成区别。

1）固定时段下径流与需水多维变量随机性描述

固定时段下多维变量随机性的描述选用多维联合分布函数。由于Copula函数不需提前假定变量之间的独立或相关关系，通过该函数的参数值大小可反映多维变量之间的相依关系或独立关系，故本研究选用Copula函数构造多维变量的联合分布函数，以此描述径流（，m³/s）与需水（，m³/s）多维变量的随机性。

式中(,)为径流与灌溉需水的联合概率，()、()为径流与需水的边缘分布函数，通过基于多评价准则的综合指数法从备选概率分布中优选所得；q、w分别为长系列情况下月的径流与需水；(x< q≤x)表示q处于[x,x]区间的概率，此处[x,x]表示的是公式（2）对径流离散的个状态中的某个状态的上下限；(x< w≤x)表示w处于[x,x]区间的概率，[x,x]表示的是对需水离散的个状态中的某个状态的上下限；θ、θ分别为边际分布函数()、()的参数集。

若固定时段下径流与需水不相关，则

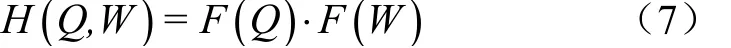
2）相邻时段间径流与需水过程关联性描述

以此次研究涉及的径流与需水多维随机过程为例，时段间水资源供需状态转移概率P{[(Q(),W()] |[(Q(),W()]}计算方法如下：

记时段径流处于状态（即公式（2）中对径流离散的个状态中的状态，该状态下径流的上下限区间为[x,x]，公式可表示为Q() =x<q≤x）的概率为(Q())，其公式为

故，在时段径流处于状态条件下，时段+1径流处于状态（即公式（2）中对径流离散的个状态中的状态，该状态下径流的上下限区间为[z,z]，公式可表示为Q() =z<q≤z）的概率为(Q()) =(Q()|Q())，其公式为

同理，时段需水处于状态（即W() =xw≤x）的概率(W())为

对于上述线性思维模式影响下所造成的诸多历史事实的长期被“遮蔽”和歪曲，学界也不乏反思，如王瑞来《宋代士大夫主流精神论—以范仲淹为中心的考察》一文：

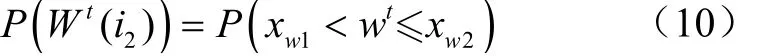
故，时段需水处于状态条件下（即(W())），时段+1需水处于状态（即W() =zw≤z）的概率为(W()) =(W()|W()) ，其公式为

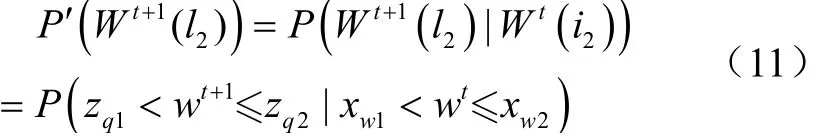
考虑到变量与的关联性，故时段+1多维变量处于状态[Q(),W()]的联合概率[Q(),W()]为

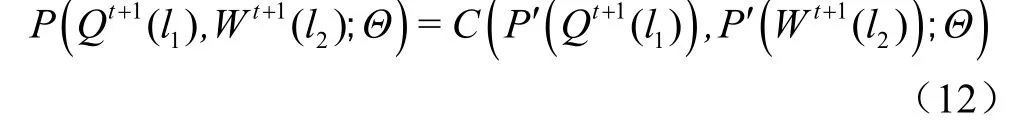
式中[Q(),W()]表示的是在时段多维变量处于状态[(Q(),W()]条件下，时段+1多维变量处于状态[Q(),W()]的条件概率P{[(Q(),W()] |[(Q(),W()]}），即

其中，式（9）与式（11）基于Copula函数的条件概率公式（式（1））计算；式（12）采用基于Copula函数的联合概率计算。

若多维过程（,）彼此独立，则

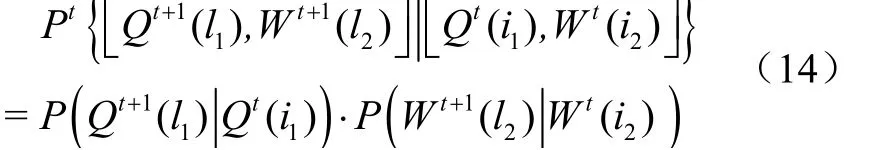
多维过程的一步状态转移矩阵为P一般式可写为

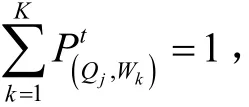
2 考虑多维过程关联性与随机性的随机动态规划算法

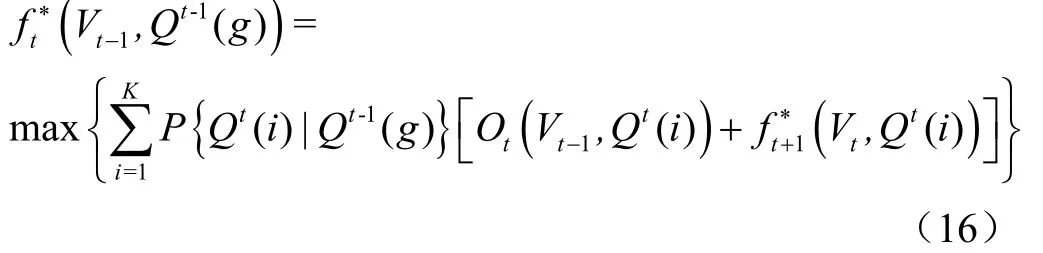
式中f(V, Q())表示-1时段入库径流为Q()、水库库容为V情形下从时段到调度期末的最优余留期效益；{Q()|Q()}表示时段-1时入库径流为Q()条件下时段入库径流为Q()的概率；O(V,Q())是当前时段入库径流为Q()时的优化调度目标值；f(V, Q())表示时段入库径流为Q()、水库库容为V情形下从+1时段到调度期末的最优余留期效益。

类比可得多维随机过程（以径流与需水二维随机过程为例）下，随机动态规划递推公式如下：

式中f(V,(Q(),W())) 表示-1时段入库径流为Q()、需水为W()、水库库容为V情形下从时段到调度期末的最优余留期效益；{[Q(), W()]|[Q(),W()]}表示时段-1时入库径流与需水为[Q(),W()]条件下时段入库径流与需水为[Q(), W()]状态的概率。

一维随机过程与多维随机过程时段间的状态转移示意图如图1所示。

图1 一维与多维随机过程下的状态转移过程 Fig.1 State transition process of one-dimensional and multi-dimensional stochastic process

3 实例研究

本文以泾河流域东庄水库为例，水库总库容32.76亿m，调节库容5.78亿m，为不完全年调节水库，死水位与正常蓄水位分别为756、789 m。水库供水对象主要为城镇生活用水、工业用水与灌区灌溉用水。其中，城镇生活与工业用水多年平均用水量2.13亿m，年内变化较为均匀，且坝前取水占65%，供水时优先满足二者用水要求；径流序列采用1960—2013年还原后的天然入库径流序列；灌区灌溉用水量计算方面，首先采用国际粮农组织（FAO）推荐的Penman-Monteith方法和作物系数法计算作物需水量和净灌溉需水量，然后不同作物种植面积乘以对应作物净灌溉需水量并除以灌区灌溉水有效利用系数（以0.65计算）。研究以农业灌溉用水缺水量最小为目标，约束条件包括水量平衡约束、水库水位约束、流量约束及变量非负约束。

3.1 数学模型

1）目标函数

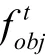
2）约束条件

① 水量平衡约束

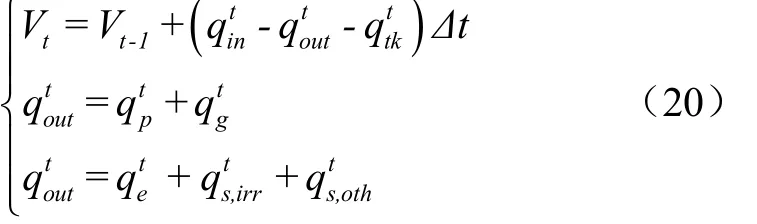
式中V表示时段末水库库容，m；q表示时段水库来水流量，m/s；q表示时段水库出库流量，m/s；q表示时段水库上游取水流量，m/s；q表示时段水库发电流量，m/s；q表示时段水库弃水流量，m/s；q表示时段水库下游河道生态流量，m/s；q表示时段水库的灌区供水流量，m/s；q表示时段水库其他供水流量（如工业及生活），m/s。

② 水位约束

式中Z为时段末水库允许消落的最低水位，m；Z为时段末水库允许达到的最高水位，m。该最高水位在汛期为防洪限制水位，在非汛期则为正常蓄水位。、Z分别为水库整个调度期初、末水位，Z为水库的起调水位（通常为死水位），m。

③ 流量约束

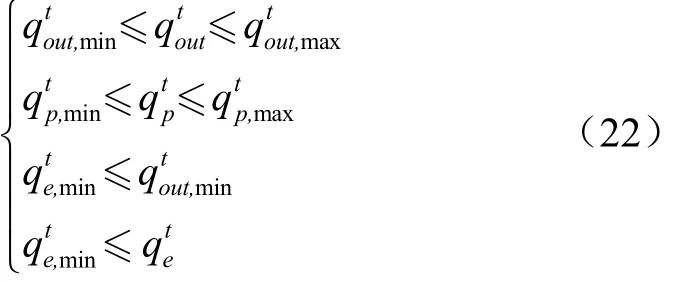
式中q、q为时段水库允许的出库流量最大值及最小值，m/s；q、q为时段水库发电流量最大值及最小值，m/s；q为时段水库下游河道所需最小生态流量，m/s。

④ 变量非负约束。调度模型中所有的变量均大于等于0。

3.2 径流与需水过程随机性与关联性结果分析

采用Gam、Logn、Gev、Weibull、Norm、Exp拟合1960—2013年各月的径流与需水数据，应用基于多评价准则的综合指数法选择适宜的概率分布函数，该方法的统计指标值越小表明该概率分布函数拟合随机变量的效果越优。基于多评价准则的综合指数法的统计指标结果见表1。由表可知，表征径流随机性的适宜概率分布函数不同月份之间差异较大，整体来看，Logn分布与Weibull分布函数选择较多；需水方面，大多数月份下，Gev分布函数是描述需水随机性的适宜函数。

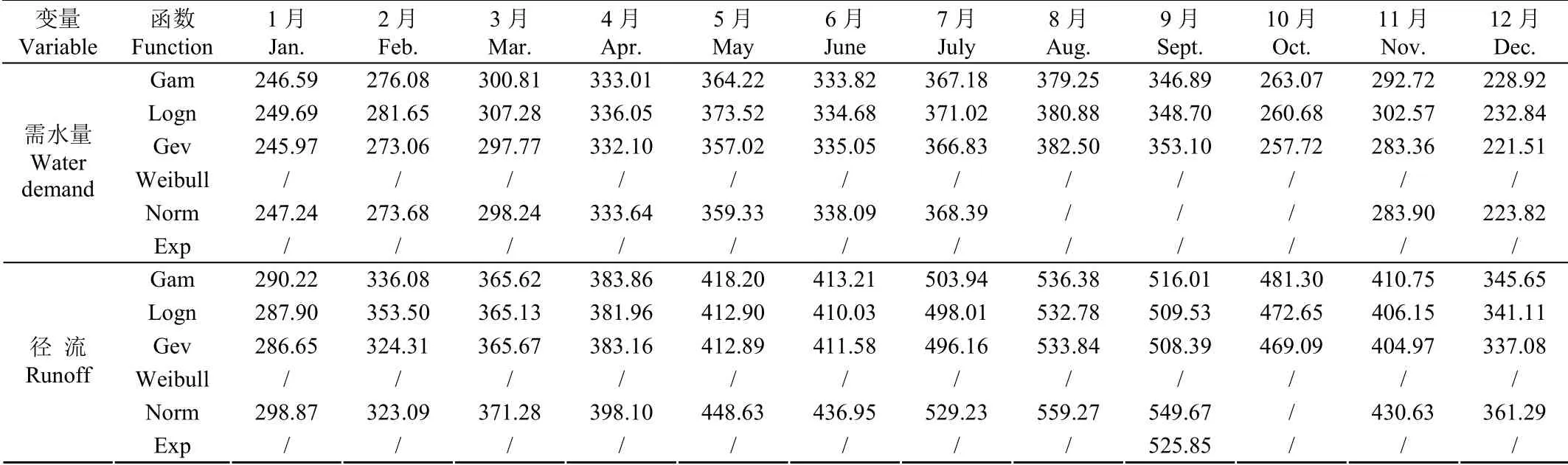
表1 基于多评价准则的综合指数法统计指标 Table 1 Statistical index obtained by comprehensive index method based on multiple evaluation rules

采用肯德尔秩相关系数描述径流、需水过程时段之间的关联性，结果见图2。由图可知，径流方面，除却6 —7月、7—8月外，其余月份之间径流过程呈显著性相关；灌溉需水方面，1—2月、5—6月、7—8月以及12—1月四个相邻时段灌溉需水相关性显著，其他时段间，灌溉需水相关性不显著。故，构建多维随机动态规划模型时，根据相邻时段间径流与需水的相关程度统计特性，需选择性地采用适宜Copula函数表征一维变量时段之间关联性。

图2 径流与需水随机过程时段之间关联性分析。 Fig.2 Relevancy analysis of runoff and water demand process at adjacent time

采用Cramer-von Mises方法选择适宜的Copula函数，以此表征径流、需水时段之间关联性，结果表明：径流方面，依照图2中所述时序，1—2月、2—3月、3—4月、4—5月、5—6月、8—9月、9—10月、10—11月、11 —12月、12—1月时段间径流的适宜Copula函数依次为Frank、Frank、Gumbel-Hougaard、Gumbel-Hougaard、Frank、Clayton、 Frank、Gumbel-Hougaard、Gumbel-Hougaard与Frank；灌溉需水方面，1—2月、5 —6月、7—8月、12—1月时段间灌溉需水的适宜Copula函数依次为Gumbel-Hougaard、Gumbel-Hougaard、Clayton、Frank。采用如上Copula函数推求时段之间变量状态转移概率，节选5—6月为例，结果如图3。以图3a为例，5月径流为7 m/s左右，转移至6月时，径流为6 m/s的概率最大，78 m/s时的可能性最小；同样，5月径流为200 m/s左右，转移至6月时，径流为78 m/s的概率最大，小于78 m/s情形下的概率逐渐减小。通过查阅该图，实际生产管理人员可获取不同月份之间径流状态转移概率，推算在当前月份的径流状态下，下月流域发生不同状态径流的可能性。

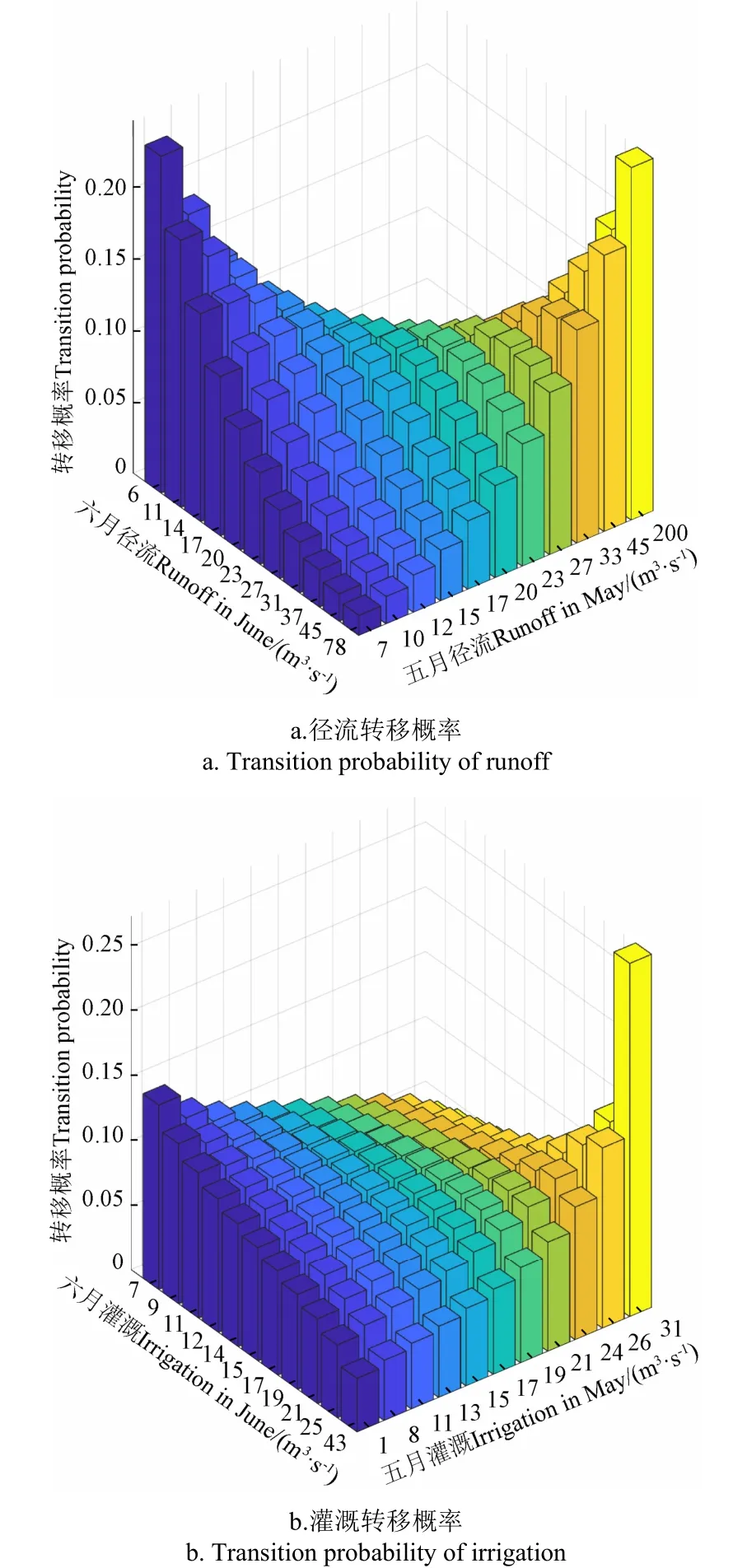
图3 5—6月径流与需水状态转移概率矩阵 Fig.3 State transitional probability matrix of runoff and water demand from May to June

采用肯德尔秩相关系数诊断二维随机变量径流与需水各个时段相关性，结果表明4月、5月、6月、7月、9月、10月径流与需水呈显著性相关，其余月份二者间相关关系不显著。在此基础上，选择适宜Copula函数描述相关性显著月份的径流与需水联合概率分布，相关性不显著月份径流与需水的联合概率采用边缘概率分布函数相乘方式获得。结果表明，由于径流与需水之间的负相关性，Frank Copula函数是拟合各月径流与需水相依关系的最优Copula函数。以5月份为例，采用Frank Copula函数表征径流与需水二维变量的联合分布，结果见图4。以图4中的累积概率分布函数（CDF，Cumulative Distribution Function）曲线为0.1为例，由于径流与需水之间的负相关关系，需水大、径流小的组合与需水小、径流大的组合位于同一累积概率分布曲线上。

图4 5月径流与需水二维联合概率分布 Fig.4 Two dimensional joint probability distribution of runoff and water demand in May

二维随机变量时段之间关联性通过二维组合过程的状态转移矩阵描述。图5展示了采用公式（14）、公式（15）计算得到的在考虑关联性（相关）与不考虑关联性（独立）两种情况下，5月径流与需水二维组合状态[,] = [72.47, 24.70]、[,] = [17.23, 42.04]向6月份100种[,]组合状态转移的概率。此处，100即是公式（2）中对径流与需水进行离散后的状态总数，图5中的1至100的状态数是分别将径流与需水离散为10种状态，然后两者之间互相组合，共形成100种方案。其中，的10种变化方案为5.55、12.20、14.55、20.29、26.49、34.78、48.19、78.81、161.22、374.65 m/s，的10种变化方案为0.04、1.76、2.77、5.36、7.96、10.95、14.83、21.00、30.20、78.22 m/s，以为基准，由大至小轮次组合，形成图5中的6月份[,]100种方案。

图5 考虑与不考虑径流与需水相关性时状态的转移概率 Fig.5 State transition probability between runoff and water demand with and without considering relevancy

由图可知，考虑径流与需水关联性与否两种情形下，二维随机过程状态转移概率不同，且不同转移状态下两种情形计算所得的转移概率大小不同，即考虑相关时的转移概率并不是全大于或全小于独立时的转移概率；此外，图5中两种情形下转移概率最大差别仅为0.04，差别相对较小，发生在5月的二维随机过程[,] = [17.23, 42.04]向6月的二维随机过程[12.20, 1.76]转移过程中。结合随机动态规划递推公式（式（17））可知，考虑变量关联性与否将影响最终最优水位决策的制定，具体影响程度取决于不同情形下状态转移概率的差异程度。

3.3 水库优化调度结果分析

为了对比分析考虑与不考虑径流、需水多维变量关联性对水库优化调度结果的影响，本次研究分别采用所提出的考虑径流与需水关联性、不考虑径流与需水关联性下的两种算法求解优化调度模型，推求了水库优化调度规则。两种情形下水库调度规则差别较小，图6展示了考虑与不考虑径流与需水关联性时6月份的水库水位最优策略。[,]=[10.33, 13.93]情况下，考虑径流与需水关联性与不考虑二者关联性水库水位决策有一定的差异，不考虑二者关联性（图中带正方形线条）时水库蓄存水位比考虑二者关联性（图中带六角形线条）时水库蓄存水位较低；其余[,]情况下，考虑与不考虑二者关联性时，水库水位最优决策过程无变化，故在图6中重合。

图6 考虑径流与需水关联性的六月份水库最优决策 Fig.6 Optimal reservoir operations in June considering the relevancy between runoff and water demand

将长系列的来水与需水数据输入水库优化调度规则，发现当考虑变量关联性时，长系列下缺水总量为10.37 亿m，不考虑时，缺水总量为10.49亿m，考虑多维变量关联性较不考虑时水库调度的优化目标（即缺水总量）更优，缺水总量相对差距0.12亿m，差别较小，差距量占缺水总量（10.37亿m³）的1.16%。该结论与黄强的研究结论一致（其发现采用独立随机过程或考虑相邻时段径流相关关系的简单马氏过程对水库优化调度成果的影响不大），其原因主要为：考虑多维变量关联性影响时，其核心是对随机动态规划算法的递推公式（公式17）中的状态转移概率产生影响，考虑二者关联性影响时，状态转移概率{[Q(), W()]| [Q(),W()]}采用公式（12）计算，不考虑二者关联性影响（即径流与需水呈独立关系）时，状态转移概率采用公式（14）计算，将状态转移概率{·}与时段优化调度结果O(·)与余留期效益f(·)之和相乘，进而递推即可得到水库调度优化目标结果。通过图5所展示的转移概率结果对比发现，考虑二者关联性影响与不考虑二者关联性影响时，状态转移概率{·}的差别较小，因此导致水库调度优化调度规则差别较小，因此将长系列径流与需水实测资料输入该优化调度规则时所得到的优化调度结果差异较小。此外，从理论上讲，径流与需水同受气象因素影响，且由于流域内气象条件的相似性，径流与需水二者之间的相关性切实存在，难以忽视，故此，建议采用考虑多维变量关联性的多维随机动态规划算法求解含农业灌溉用水的水库优化调度问题。此外，若水库以工业、生活用水等为目标时，来水与工业、生活用水之间的关联性较差，可采用本文中的公式（15）计算来水与工业、生活用水之间的状态转移概率，进而应用本文多维动态规划算法进行求解。

4 结 论

水库来水以及灌溉用水二维过程的随机性与关联性切实存在。本文利用Copula函数在表征多维随机变量的非线性相关与随机性方面的优势，描述同类变量不同时段之间的随机性以及不同变量相同时段之间的关联性，在此基础上，与传统随机动态规划算法结合，提出了考虑多维变量关联性与不考虑多维变量关联性的多维随机动态规划算法。

以东庄水库优化调度为例，结果表明，采用考虑水库来用水过程关联性的多维随机动态规划算法求解优化调度模型，缺水总量为10.37亿m，采用不考虑二者关联性的多维随机动态规划算法求解时，缺水总量为10.49 亿m，缺水量相对降低0.12亿m，考虑来用水过程关联性的结果更优，但差距较小，相对提升百分比为1.16%；考虑来用水过程关联性时的状态转移概率较不考虑二者关联性时的状态转移概率差异较小是造成优化调度结果差异较小的主要原因。考虑来用水过程关联性的多维随机动态规划算法理论上更符合水资源供需过程天然存在的随机性与关联性特征，本文建议采用考虑来用水过程关联性的多维随机动态规划算法求解水库优化调度模型。

若水库以工业与生活供水为目标，该类用水过程与水库来水过程之间并无机理上的关联性，建议采用本文所提的不考虑随机变量间关联性的多维随机动态规划算法求解。此外，本文所提的随机动态规划算法在其他领域的随机优化决策问题方面（如基于水库调度的水风光多能互补等）同样适用。未来，如何扩展二维随机动态规划算法至更高维情形，是该项研究的重点所在。