苜蓿振动压缩成型过程中的力链演变

杜海君，雷 霆，张永安，武 佩，马彦华※，布 库

（1. 内蒙古农业大学机电工程学院，内蒙古自治区草业与养殖业智能装备工程技术研究中心，呼和浩特 010018；2. 中国农业科学院草原研究所，呼和浩特 010010）

0 引 言

苜蓿块是依靠对模具内的揉碎苜蓿施压，克服物料本身的变形阻力、物料间的摩擦力、物料与模具摩擦力而致密成型。成型块不仅能有效保留苜蓿原有的营养成分，而且方便运输，是苜蓿贮存的主要形式之一。

物料在压缩成型过程中的力学行为会影响成型块的密度和压缩能耗。近年来，国内外学者对生物质压缩成型过程中的应力应变行为进行了大量研究。李永奎等基于离散元方法分析了压缩位移、模具孔径和锥角对玉米秸秆粉料在压缩过程中的压缩与应力松弛曲线的影响。涂德浴等应用有限体积元法建立了生物质成型过程的力学特性模型，分析了物料在成型过程中各阶段的等效应力和应变的变化规律。Xin等基于弹塑性理论和接触分析原理，建立了秸秆类生物质的压缩过程三维仿真模型，揭示了压缩过程的蠕变规律。上述对生物质压缩过程力学行为研究主要侧重于在外载荷作用下颗粒物料体系表现出来的受力及变形等宏观力学行为。

颗粒物料体系表现的静态堆积特性和动态流变特性都与细观尺度力链的结构及演变规律直接相关。力链不仅是宏观颗粒体系的细观力学行为，也是外载荷的传递路径。学者们主要采用接触式试验和离散元模拟两种方法，对岩土、金属粉末及颗粒在剪切、压缩状态下的力链结构及其演变过程进行了研究。

孙其诚等对重力作用下的颗粒物质进行了离散动力学模拟，对力链分布特征、接触力规律做了量化分析。Zhang等试验研究了剪切系统中的力链分布，与等速压缩系统相比，力链分布略有不同。Iikawa等利用光弹法研究颗粒被压实过程中力链结构演化过程，发现颗粒间力的增加与力链方向的无序性呈负相关。张炜等利用离散元法对金属粉末在高速压制中力链演变规律进行分析，探究细观力链和宏观体系内应力间关系。左苗苗利用离散元法对高频振动下固体颗粒力链演变进行分析，在振动条件下传力过程为平衡—打破—新平衡的反复过程。

针对于生物质压缩过程中的力链研究鲜少报道，李震等基于离散元法对沙柳细枝颗粒进行了单轴静态压缩，分析了压缩过程中的力链结构及其演变过程。力链是一种随机的网络结构，力链网络不仅与颗粒物料本身的性质有关，还受外部载荷等外界控制参数的影响。在苜蓿压缩过程中，叠加的振动力场将影响力链的分布特性及其演变规律。因此本文采用离散元模拟方法进行苜蓿振动压缩过程力链结构及演变过程的研究。从细观尺度分析振动压缩过程中被压缩物料的力学特性，进而探究振动对压缩过程的作用机理，优化振动压缩工艺参数。

1 离散元仿真与模型验证

1.1 接触模型

离散单元法（Discrete Element Method，DEM）是由Peter Cundall在1971年提出的一种颗粒物料微观力学分析方法，其建立在牛顿第二运动定律基础上。颗粒间的接触力学行为通过离散元中的接触模型来描述。根据揉碎苜蓿本身的生物力学特性，选择被压缩物料间的离散元接触模型为 Edinburgh Elasto-Plastic Adhesion（EEPA），物料与模具之间的接触模型为Hertz-Mindlin（no-slip）无滑动接触模型。

1.2 模型与试验

采用课题组自主研发的液压活塞式压缩试验台进行振动力场作用下苜蓿压缩成型试验研究。试验系统工作原理如图1所示。液压系统带动压缩活塞以4.81 mm/s的速度对苜蓿进行压缩，振动系统提供振幅为1 mm，振动频率分别为0 （无振动）、15 Hz的振动，经振动杆传递到被压缩物料底部，由NI USB-6210数据采集卡采集、记录压力传感器SYL17（量程：0～50 MPa，精度：0.02 MPa/10 MPa）的信号。

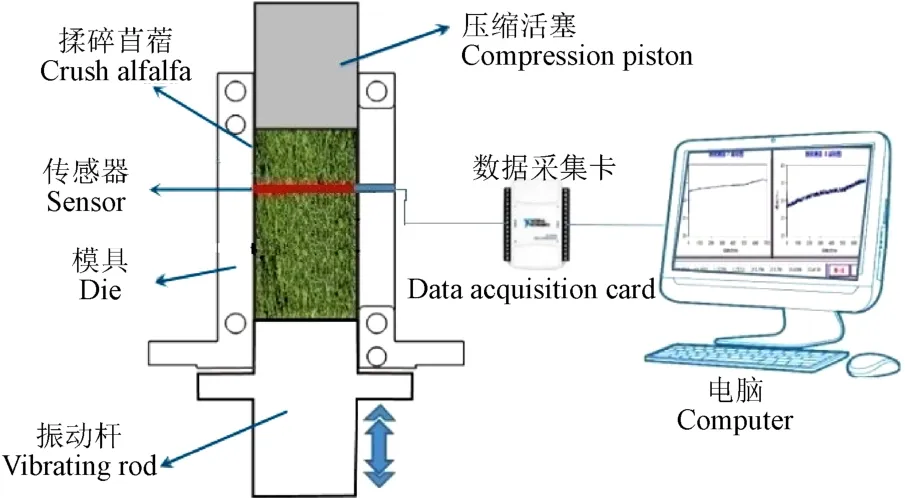
图1 试验系统工作示意图 Fig.1 Schematic diagram of test system

试验材料选用2021年8月生产于内蒙古农业大学试验田的紫花苜蓿，阴干晾晒后将其揉碎。筛分得到半径为0.6～0.8 mm的苜蓿颗粒，采用GMK-3308型干草水分测定仪测量其含水率，约为18%。

随机选取压缩物料内任一位置的压缩应力进行验证试验。为保证每次试验压力传感器放入的位置一致，试验时先将17 g揉碎苜蓿颗粒喂入模具内，然后放入压力传感器，再填入8 g苜蓿。启动液压系统，驱动活塞以4.81 mm/s的速度下行，同时启动机械振动装置，实现振动压缩，当活塞下行到下行程止点后回程，停止振动，完成一次压缩。

随机取40组样本测量揉碎后苜蓿颗粒长度和直径，根据测量结果将颗粒分为大小两组，分别取两组颗粒尺寸的均值来建立苜蓿颗粒模型。小颗粒尺寸半径为0.6 mm，长度为5.5 mm；大颗粒尺寸半径为0.8 mm，长度为8.6 mm，如图2a所示。

图2b为成型模具实物图，模具内径40 mm，高度120 mm。图2c是根据模具实际几何尺寸及约束条件建立的压缩系统离散元仿真模型，主要由压缩活塞、成型模具、揉碎苜蓿、振动杆组成。

图2 模具实物图及压缩系统离散元仿真模型 Fig.2 Photo of die and compression system DEM simulation model

仿真参数主要包括苜蓿、模具的物理特性参数，及由标定试验得到的苜蓿间、苜蓿与模具间的接触参数，如表1所示。

表1 材料参数 Table 1 Material parameters

根据揉碎苜蓿的物理特性，设置EEPA接触模型参数中的表面能（Surface energy）=8.5 J，接触塑性比（Contact plasticity ratio）=0.8，粘接力黏附指数（Tensile exp）=20，切向力刚度（Tangential stiff multiplier）=0.67，刚度系数（Shear modulus）=1.5 MPa。

1.3 模型验证结果

利用离散元法对压缩过程中颗粒力学特性进行准确的描述，需要确定合理的模型及参数。但因实际散体形状的不规则性、模型简化及部分参数的平均化会造成模拟结果和实际试验结果的差异，因此利用压缩试验来验证离散元模型的可靠性。

将模拟得到的压缩应力随时间变化数据与压缩试验数据进行对比，通过绝对误差来验证离散元模型的有效性，结果如图3。

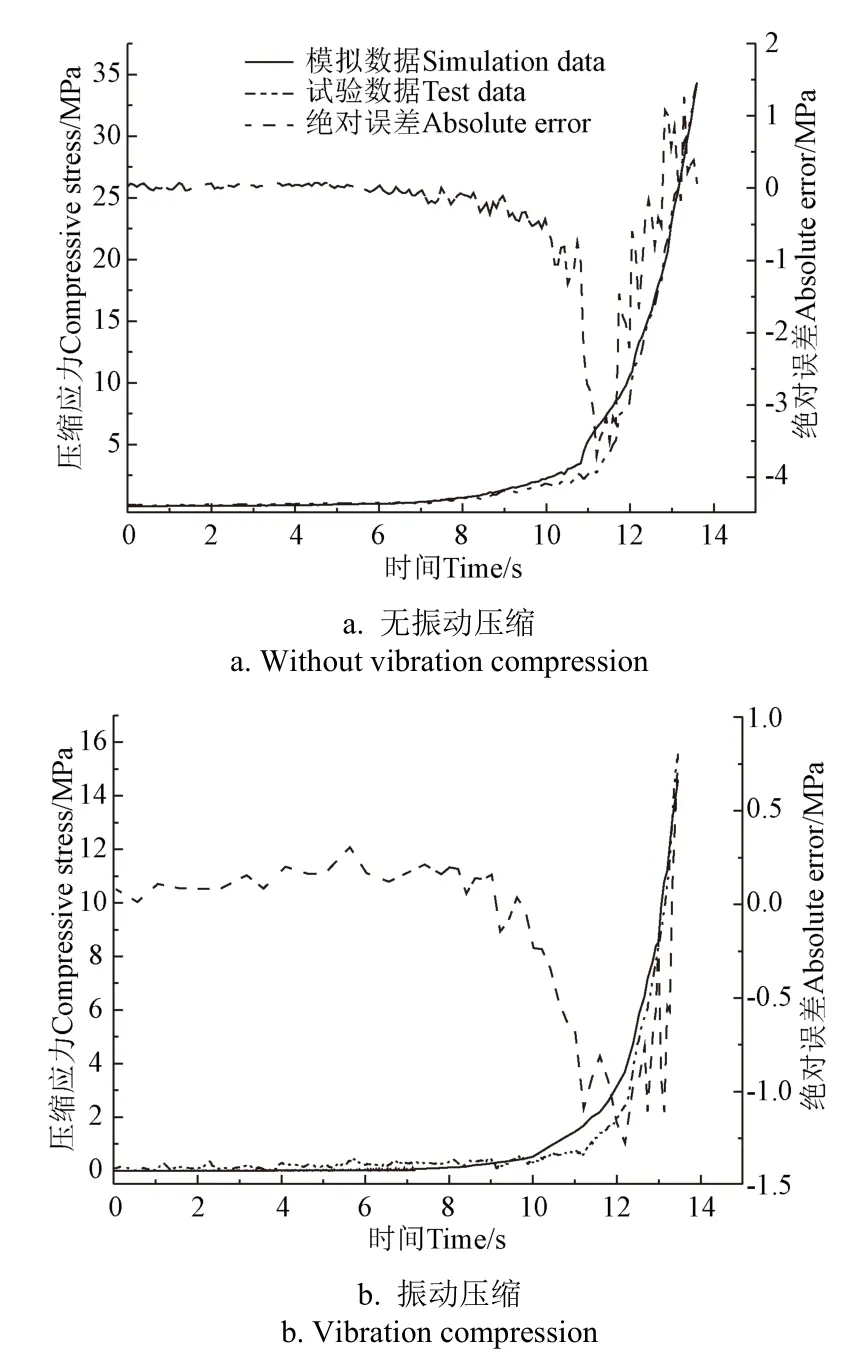
图3 有无振动压缩时压缩应力模拟与试验数据对比 Fig.3 Comparison of compressive stress simulation and test data with and without vibration compression

将试验数据和仿真数据进行双样本T检验。在显著性水平=0.05下，假设N为离散元模拟和试验测得压缩应力数据方差相等，N为两者方差不相等。经假设检验知，无振动压缩试验数据和仿真数据均值相差0.293，振动压缩试验数据和仿真数据均值相差0.253，在显著性水平=0.05下接受N，即在相同试验条件下，被压缩物料内同一位置的压缩应力模拟数据与试验数据无显著性差异，认为利用建立的离散元模型及模型参数进行揉碎苜蓿压缩过程力学行为的仿真试验是可行的。因此本文将借助上述离散元模型及模型参数来模拟揉碎苜蓿颗粒压缩过程中力链结构及演变机制。

2 力链演变机制

2.1 轴向力链随时间演变分析对比

为了研究压缩过程中压力的传递机理、力链结构及其动态演变过程，沿轴向将模具内苜蓿颗粒均分为5层，各层设置一个测量块，用于测量该层接触力大小。从上到下依次按高度设置的测量块为1、2、3、4、5，如图 2c所示。

图4a、4b分别为无振动压缩和振动压缩条件下测量块1～5模拟测得的各层物料轴向平均压缩力随时间的变化规律。揉碎后苜蓿为长条状颗粒，将其喂入模具后由于苜蓿间的架拱作用使得颗粒空隙较大，同时苜蓿本身的密度较低，在活塞开始压缩的一段时间内，压力较小，几乎为零。随着颗粒间隙被填充，各层物料间轴向压缩力开始显著增加。在不同的压缩条件下，物料各层压缩力的变化有所不同。

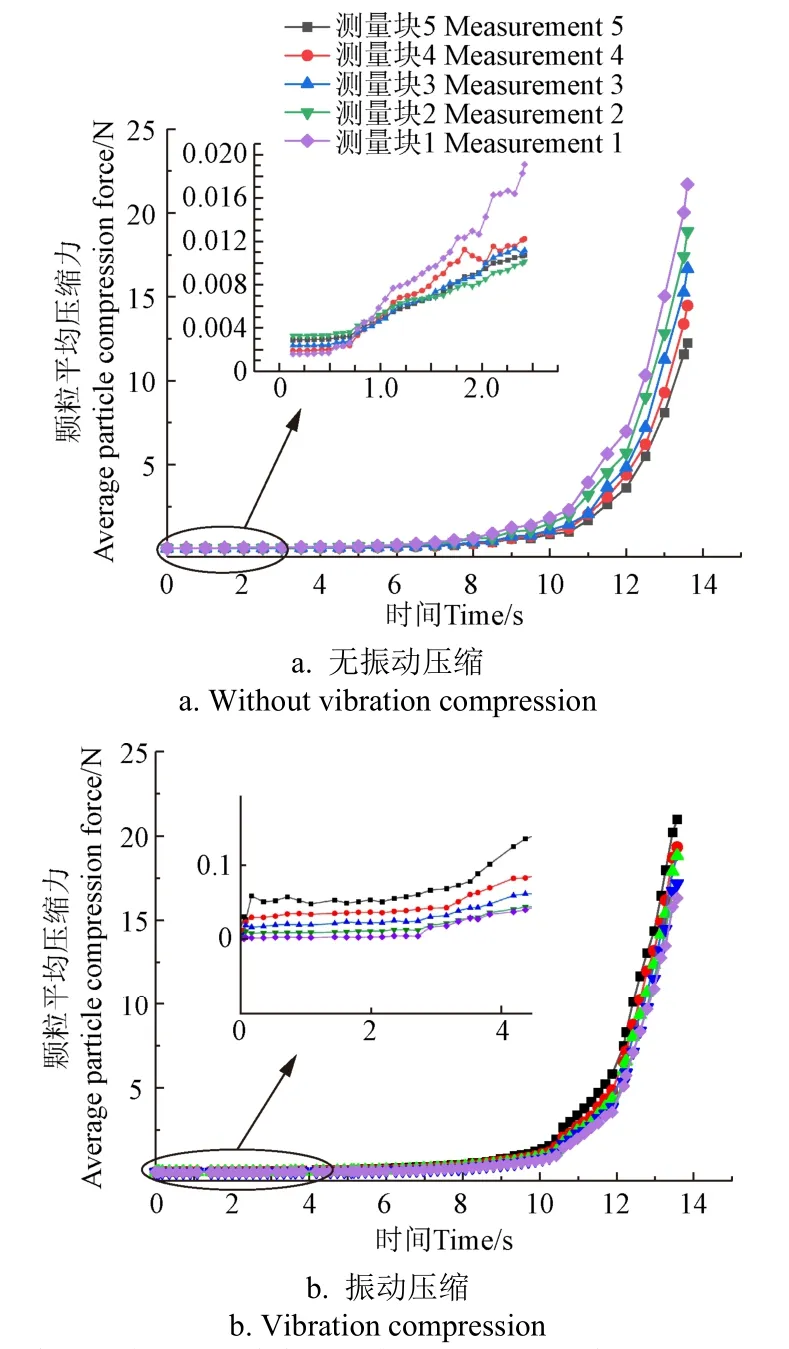
图4 有无振动压缩过程轴向各层苜蓿颗粒平均压缩力 随时间变化曲线 Fig.4 Curves of average compression force – time in alfalfa particles layer with and without vibration compression

由图4a可知，在0～0.5 s时间段，物料内压缩力由上层向下逐渐增加，各层压缩力差值较小，此阶段物料主要受重力作用，使得下层物料较上层物料密度高，接触紧密。在0.5 ～1.5 s时间段，最大压缩力位置开始经历由下层向上层过渡的过程。0.5 s时刻，在压缩活塞的作用下，上层物料压缩力开始打破初始平衡，产生一阶跃应力，随后第2层至5层逐渐出现微小的应力突变；0.65 s左右，上层压力值以较大速率增加，在很短时间内，达到最大，但各层压缩力差值不大。6 ～13.6 s时间段，各物料层压缩力加速变大且各层间压缩力差值增加，压缩力出现由上向下递减的趋势，此阶段为压实物料阶段。

模具内物料在活塞轴向压缩和振动力场共同作用下，如图4b。开始压缩前，物料在重力作用下，下层物料密度较高，最大压缩力由下向上递减；在0～0.2 s时间段，揉碎苜蓿主要在重力及振动力的作用下，打破静止状态的力平衡，压缩力波动上涨，下层物料压缩力涨幅较大。0.2 s后，物料间压缩力进入到平缓阶段，直到2.8 s左右，第1层物料受压缩活塞作用明显，压缩力开始快速增加，1、2层压缩力接近相等。在整个压缩过程中，各层压缩力始终保持由下向上递减的变化规律。

在达到最大压缩行程时，各层物料内压缩力的数值如表 2所示。由表可知，无振动压缩时，测量块1、5间的压缩力差值为9.46 N；振动压缩时，测量块5、1间的压缩力差值为4.67 N。说明振动均化了物料内的压力，有利于力的传递。

表2 各测量块内平均压缩力 Table 2 Average compression force in each measuring block N

力链演变过程映射了宏观力学的变化规律。力链是外载荷和重力作用下颗粒体系内颗粒单元相互接触产生大小不一的接触力传递路径。图5是压缩过程中轴向力链演变过程，颜色蓝、绿、红，代表力链强度依次增加。

无振动力场作用下，压缩初始时刻，在重力作用下，下层物料间接触紧密，出现了较强的力链；随着压缩活塞下行，作用于上层物料的压力逐渐加大，0.5 s时，上层物料内开始形成强力链，并向下传递，1 s左右，物料内各测量层强力链较均匀；在6 s后，强力链开始集中于物料顶层，并随着压缩行程加大，强力链向下延展。在13.6 s时，即压缩完成时刻，强力链几乎延伸到物料下层，但是总体分布依旧由顶部到底部逐渐稀疏，如图5a所示。

与无振压缩过程中力链结构演化对比，振动压缩过程中力链结构演变过程有所不同，见图5b。初始状态，在重力作用下，底层力链强度较大；随着压缩过程进行，由于物料在重力和振动力的作用下，底层物料不断致密，颗粒间接触力增加，形成的强力链依然集中于底部，并向上传递；2.9 s左右，活塞对上层物料的作用力增加，开始出现强力链，并向下传递；之后模具内物料受到轴向压力和振动力作用，力链由上下两端向中间传递，下部振动产生的力链传递距离较大。在压缩行程结束时物料各层内强力链分布趋于均匀。综合颗粒平均压缩力动态变化与力链分布（图4与图5），在相同工况下，两者演化过程具有一致对应关系。

图5 有无振动压缩时轴向力链演变过程 Fig.5 Evolution of axial force chain with and without vibration compression

颗粒间相互作用的接触力大小不一，通常用颗粒间平均接触力作为判断强弱力链的依据。当颗粒间接触力>时，颗粒间接触为强接触，多个强接触连接形成强力链；反之为弱接触，弱接触形成的力链为弱力链。强接触越多，物料被压缩时需要的压缩力就越大。通过EDEM2020数据分析软件，得到压缩结束时成型块内强接触的轴向分布，如图6所示。无振动压缩苜蓿时，成型块内含有39 258个强接触，强接触由上到下逐渐减少，分布不均匀；振动压缩条件下，成型块内含有38 079个强接触，强接触分布较均匀。从强接触的数量以及分布现象可知，压缩过程中叠加振动可以降低压缩力，提高成型块稳定性，其原因是振动力场促使苜蓿颗粒局部运动，调节颗粒间相对位置关系，降低“成拱现象”，使颗粒间受力更为均匀。

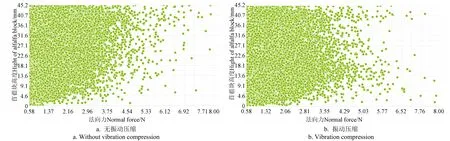
图6 有无振动压缩结束时苜蓿块内强支撑沿轴向分布图 Fig.6 Axial distribution of strong contacts in alfalfa block at the end of compression with or without vibration

通过颗粒压缩力动态变化过程与力链分布、演变过程可知：振动力场使物料各层间的压缩力差值变小，力链分布更均匀。压缩过程力链演变传递方向不同，无振动压缩时，力链由上向下传递；振动力场作用下，力链由上、下两端向中间传递，相比于活塞静压力，振动产生的力链传递距离远。

2.2 径向力链演变

无振动压缩及振动压缩过程中径向方向不同时间节点力链演变分别如图7a、7b所示。

图7 有无振动压缩时径向力链演变过程 Fig.7 Evolution of radial force chain with or without vibration compression

对比图7a、7b可知，初始压缩时刻，由于颗粒体系密度较低，在模具内中间物料层的整个径向方向几乎不存在强力链；随着压缩行程的增加，强力链出现在芯部周围，并且逐渐增强向外传递，最终强力链向模具壁面延伸，在整个径向方向强力链分布趋于均匀。在相同时刻，振动压缩条件下，强力链的分布密度及强度均小于无振动压缩时产生的强力链。说明振动可以均化被压缩物料的内应力，使其产生的膨胀变形以及变形力均小于无振动压缩，因此成型块出模后能够很好地保持其原有的形状。

2.3 孔隙率

孔隙率是指致密成型块中空隙体积的占比。成型过程中孔隙率的变化规律间接反映了颗粒体积占比的变化，其直接影响力链的结构和稳定性。利用EDEM2020软件中传感器模块得出压缩过程中轴向孔隙率变化规律如图8。

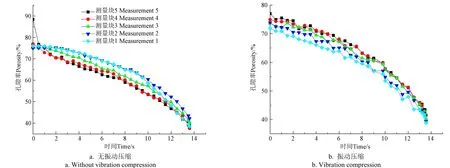
图8 有无振动压缩时轴向各层苜蓿孔隙率变化曲线 Fig.8 Porosity curves of each alfalfa layer in the axial direction with or without vibration compression

无振动压缩过程中，在开始时刻顶层物料孔隙率高，孔隙率由上向下逐层递减，主要原因是揉碎苜蓿处于自由堆积状态，在重力作用下顶部最为松散。随着压缩活塞下行，顶部孔隙率随即发生突变，上两层孔隙率降为最低，说明压缩力使接近压缩力作用点处的物料首先产生相对运动及变形。在压实中后期，因为模具底部强约束而产生的反作用力，使底部揉碎苜蓿的孔隙率下降速度加快；最终出现上层、下层物料孔隙率较小，中间偏下层物料空隙率较大。

振动压缩过程中，在开始时刻顶层物料孔隙率最高，逐层递减。在压缩活塞轴向压力以及振动力场的作用下，模具内各层物料的孔隙率基本保持由上向下的递减趋势。相比于无振动压缩，在压缩行程末，各层物料孔隙率差值较小，无振动压缩时松散与密实两层之间的孔隙率绝对差值为3.65个百分点，而振动压缩松散与密实两层之间的孔隙率绝对差值为2.71个百分点，说明振动不仅增强了力链的传递，同时振动有利于增加物料被压实的均匀性。

3 结 论

1）基于离散元仿真模型，进行了揉碎苜蓿压缩力分布及传递研究。无振动压缩过程中，在压实阶段压缩力从上向下逐层递减分布；振动压缩时，整个压缩过程中压缩力由从下向上逐层递减分布。物料内各层压缩力分布不均匀，无振动力场作用下，压缩力最大差值为9.46 N，振动力场作用下，压缩力最大差值为4.67 N。说明振动有利于应力传递。

2）无振动压缩过程中，揉碎苜蓿内轴向力链从上至下传递，强力链分布密度亦从上到下逐层递减，压缩苜蓿到最大程度时，成型块内强接触数量为39 258个；振动压缩前期，力链由下向上传递，后期则是上下同时向中间传递，强力链分布较为均匀，压缩苜蓿到最大程度时，强接触为38 079个。径向方向随着压缩行程的增加，强力链出现在芯部周围，并且逐渐增强向外传递，最终强力链向模具壁面延伸，在整个径向方向强力链分布趋于均匀。在相同时刻，振动压缩条件下，强力链的分布密度及强度均小于无振动压缩时产生的强力链。

3）在无振动压缩时轴向各层孔隙率表现为上层、下层物料孔隙率较小，中间偏下层物料空隙率较大，疏密两层孔隙率绝对差值为3.65个百分点；振动压缩条件下模具内各层物料的孔隙率基本保持由上向下的递减趋势，疏密两层孔隙率绝对差值为2.71个百分点。相比于无振动压缩，在压缩行程末，各层物料孔隙率差值较小。