基于近红外光谱技术的眉茶拼配比例预测方法
宋 彦,汪小中,赵 磊,张 叶,宁井铭,程福寿
(1. 安徽农业大学工学院,合肥 230036;2. 安徽农业大学茶树生物学与资源利用国家重点实验室,合肥 230036;3. 黄山一品有机茶业有限公司,黄山 245000;4. 安徽省智能农机装备工程实验室,合肥 230036)
0 引 言
拼配是出口炒青绿茶在精制加工过程中的一项作业,需要根据各花色等级产品的质量要求,将各类原料茶按一定比例合理拼合,组成各花色等级的成品茶。采用拼配作业的原因在于,由鲜叶初制加工的毛茶因产地、栽培水平、加工工艺等因素不同,其品质不但与标准样存在一定差异,而且不同来源、批次的毛茶质量也有明显差异。而商品茶要求质量规格化、标准化,因此首先需要将毛茶制成半成品茶,进一步参照商品茶标准样,通过拼配作业拼合各原料茶,达到保证质量一致性、扩大产量、充分利用原料的目的。
目前茶叶拼配仍然采用专家拼配的方法,即首先由经验丰富的拼配专家对原料茶进行感官审评,然后试拼小样,与标准样进行比对后,再优化拼配方案。吴步畅等探讨了采用无性系良种茶树鲜叶加工拼配径山茶的可行性,采用了理化分析与感官分析相结合的方法评价拼配茶的质量。针对滇红工夫茶的拼配问题,郑际雄等提出了两种有效的成品茶拼配方法,并介绍了拼配实例。中国大宗出口绿茶,广泛采用拼配技术,杨选民等从绿茶拼配技术的原则、流程、技术要点出发,阐述了绿茶拼配中的主要技术要点。通过上述研究发现,茶叶拼配作业中,如何设计优化拼配比例,是拼配作业的关键问题。
在拼配作业中,一方面要求拼配茶的质量要满足标准样要求,另一方面企业也希望实现降低拼配原料的综合成本,充分利用库存原料。部分学者将这一问题抽象为多目标优化问题,如Fomeni等针对茶叶生产中的拼配问题,提出了一种多目标优化方法,并重点讨论了当原料成本和品质要求存在矛盾时的权衡优化问题。国内也有于杰等学者针对抹茶的智能拼配问题,提出了基于线性规划的拼配比例计算方法。
总结上述国内外现状,在茶叶拼配比例设计,成本与库存优化等方面都取得了一定成果。在拼配作业中,对茶叶质量的审评是贯穿其中的,无论是对各种原料样的审评,还是对试拼小样的品质评价。而目前研究成果中,对于茶叶品质的评价仍然采用人工感官审评的方法,虽然符合现行国家标准的要求,但是结果容易受到审评人员主观影响。如何在客观评价商品茶与原料茶品质的基础上,进一步计算其拼配比例,仍然是困扰国内外学者的难题,相关的研究成果也极为少见。
近年来,国内外学者利用多种传感手段,如近红外光谱技术、高光谱技术、电子鼻/舌用于茶叶或者其他农产品的品质检测,取得了很多成果。其中近红外光谱技术不但可以用于农产品等级的定性识别,如等级、产地判断,也可以用于其主要化学成分的定量分析,能够更为全面表征茶叶的品质。这为解决拼配比例计算问题,提供了新的思路。宁井铭等以祁门工夫红茶为例,提出了一种基于光谱数据的拼配比例计算方法。
本文面向炒青绿茶中典型产品——眉茶的拼配比例设计问题,利用茶叶的近红外光谱数据,构建用于预测拼配比例的机器学习模型,并验证该模型的预测效果。以眉茶为研究对象,选择若干典型的半成品茶作为拼配原料,模拟拼配过程拼合了若干组拼配茶样,采集其近红外光谱数据。尽管拼配比例存在差别,但是各组茶样的近红外光谱数据呈现出高度相关性,常见的回归计算方法难以解决这一问题,本文利用深度学习技术高效的特征提取机制,提出基于卷积神经网络的特征提取方法,以期实现拼配比例的高精度计算。
1 材料与方法
本研究目的在于构建计算拼配比例的机器学习模型,将采用炒青绿茶作为试验原料,采用模拟拼配的方法,拼合若干组拼配茶样,并随机划分为训练集和预测集。采集茶样的近红外光谱数据,并利用训练集数据训练、验证拼配比例预测模型,采用拼配比例预测误差的各统计量,在预测集上测试拼配比例计算模型的有效性。
1.1 试验材料与测定方法
试验原料取自黄山一品有机茶业有限公司,该单位多年从事眉茶的生产与出口工作,产品长期出口西北非,客户对滋味品质具有较高的要求,市场偏好滋味浓强鲜爽,汤色黄橙明亮的茶叶。在拼配方案中,往往以黄山本地茶作为基准茶,彰显屯绿滋味浓厚而不苦涩的特点,调剂茶选取口感浓强,香气重的湖北小叶种茶,以及鲜爽度高,滋味平和的福建茶。根据上述方案,选取4种典型的原料茶:休宁茶上段正口,福建茶上段子口,湖北小叶种茶,歙县碎茶。上述原料着重体现了不同产地茶的滋味特点,同时外形上包含了上中下段,容重也包含了正口、子口茶,具有较好的代表性。将以上述半成品茶作为原料,按照预设比例拼配若干组茶样,并采集各原料样与拼配样的近红外光谱数据,用于训练预测拼配比例的机器学习模型,并通过预测结果与预设拼配比例的比对,验证预测模型的效果。
本文共设计25组样本,如表1所示,包含了单一茶样,2~4种茶样混合的不同形式。每组按照拼配比例表所设比例拼配至净质量500 g,并在茶盘内充分混合均匀后,密封保存。

表1 眉茶拼配比例表 Table 1 Proportion table of Mee Tea tea blending
1.2 近红外光谱数据采集
参考韦玲冬等提出的样品制备方法采集茶样的近红外光谱数据。首先,将被检测样本放置粉碎机进行研磨粉碎处理;为了减少大颗粒对漫反射的影响,将研磨后的粉末经过80目(筛网孔径小于0.180 mm)网格筛,筛选去除大颗粒茶样粉末;其次,称量3 g量的茶样粉末,并放置在定制的红外压片模具中,并在红外压片机的20 MPa压力下,压制成饼状茶样。将饼状茶样放置在近红外光谱仪(德国Bruker公司,MPA型傅里叶变换近红外光谱仪)的检测口,将近红外光谱仪切换至漫反射检测模式后,扫描检测窗口处的茶样;每次扫描完成后,将茶样旋转120°后,继续扫描,待3次扫描完成后,通过OPUS软件,求取3次扫描反射值的平均值,作为此次茶样的近红外光谱反射率。
试验过程中,对每个拼配样本制备20个子样本,共计500个样本,分别采集近红外光谱数据,用于训练和测试拼配比例预测模型。
2 拼配比例预测模型构建
在前期的研究过程中发现,尽管不同样本的拼配比例不同,但是近红外光谱数据是高度相似的。当采用传统的回归计算方法求解拼配比例时,产生了多重共线性现象,计算误差很大。在各类模式识别任务中,特征提取方法对于模型精度有较大影响,而深度学习方法能够高效、自动的从原始信号中提取关键特征,因此本文采用基于卷积神经网络和自动编码器,用于提取茶样的近红外光谱特征,进一步采用Softmax函数,预测各原料样的拼配比例。为了对比不同特征提取方法的效果,同时采用两种方法对比效果。一种是采用主成分分析(Principal Component Analysis,PCA)方法提取光谱特征,并结合Softmax函数预测拼配比例;另一种是采用PCA方法提取光谱特征,结合偏最小二乘回归(Partial Least Squares Regression,PLS)算法计算拼配比例。除了特征提取方法以外,提取的特征维度数量也对模型精度有一定影响,这也是本文需要对比、优化的关键参数。
2.1 基于卷积神经网络的特征提取方法
基于卷积神经网络的拼配比例计算模型结构如图1所示,近红外光谱数据首先输入卷积神经网络模型提取特征,进一步输入Softmax模型用于拼配比例计算。卷积神经网络的结构主要由卷积层、池化层、全连接层组成。卷积层(Convolutional Layer)是基于卷积运算的一种结构,通过卷积运算来细化输入数据的潜在特征。卷积核(filters)是卷积运算的核心,它逐行扫描光谱数据,寻找特征描述。池化层(Pooling Layer)一般是在卷积运算后,其主要作用就是提取有效特征,同时也能够减少参数的数目。全连接层(Fully Connect Layer)一般在网络结构的后面几层,将前面卷积-池化层提取的特征按照特定权重合并,作为全连接层的输入。近红外光谱数据经过卷积神经网络提取特征,输入Softmax模型,用于预测各原料样的拼配比例。
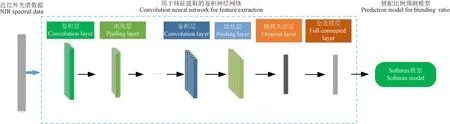
图1 基于卷积神经网络的拼配比例计算模型 Fig.1 Calculating model of blending ratio based on convolution neural network
卷积神经网络构建完成后,就需要对权值参数进行优化。目前主要的优化方法就是利用训练集数据进行反向传播,主要做法是从目标函数对上一层求偏导,利用链式法则不断向前传播,采用梯度下降法迭代更新全连接层和卷积层的权值参数。
2.2 基于自动编码器的特征提取方法
自动编码器是直接应用单层或多层神经网络映射输入数据,获得输出向量作为光谱提取信息特征,这样利用自动编码器所构建的网络提取光谱数据特征。网络主要由输入层、隐藏层以及输出层组成。在自动编码器的网络框架中,神经网络的前半部分是编码器,它主要从原始输入数据中提取特征。后一部分为解码器,在训练过程中根据提取的特征重构原始数据。基于自动编码器的拼配比例计算模型结构如图2所示,待网络训练完成后,将训练完成的网络用于光谱特征提取,同样采用Softmax模型计算各原料样的拼配比例。
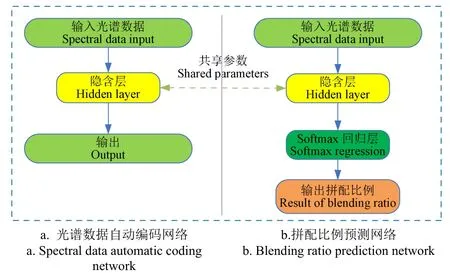
图2 基于自动编码器的拼配比例计算模型 Fig.2 Calculating model of blending ratio based on automatic encoder
2.3 Softmax模型设计
给定个训练样本(x,y),其中x表示为经特征提取算法提取的维特征向量,y为各原料拼配比例,取值为[ 0,1]之间。预测出的拼配比例向量记为y,即
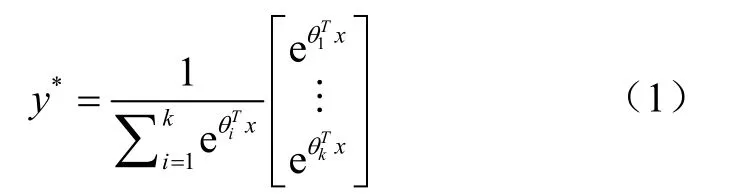
式中e为自然对数,θx为第个类别对应的值。构造对数似然函数为
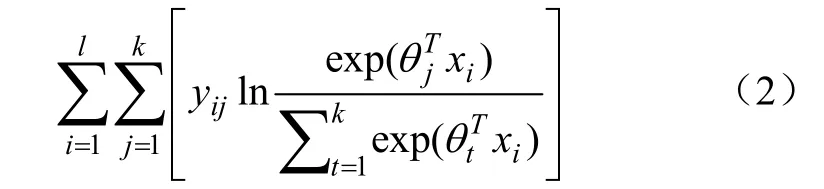
式中x为维特征向量,y为表示第个样本,第分量的值。将上式对数似然函数取极大值近似等价于下式损失函数取极小值:
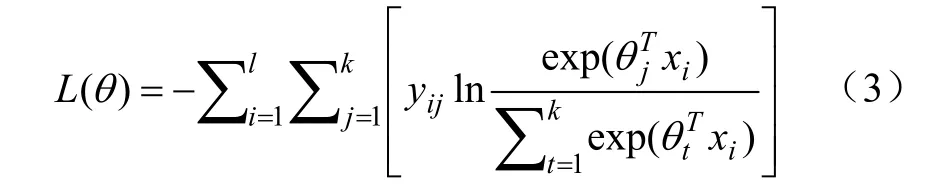

通过利用梯度下降法对损失函数的梯度值进行迭代运算,直至网络模型收敛或达到预设停止条件,完成训练。
2.4 模型训练与评价方法
本文共采集样本光谱数据500个,每个拼配比例均按照9∶1的比例随机划分为训练集(Training Set)与测试集(Testing Set)。为了充分验证模型性能对比模型参数,对训练集进行3折交叉验证,因此在训练集内部,将样本进一步划分为校准集(Calibration Set)和验证集(Validation Set)。
拟采用决定系数()、均方根误差(Root Mean Squard Error,RMSE)两项指标评价拼配比例预测模型的性能。决定系数主要用于衡量实际值与预测值之间的相关性。它的值越接近1,实际值和预测值之间的相关性就越好。其计算公式如下所示:
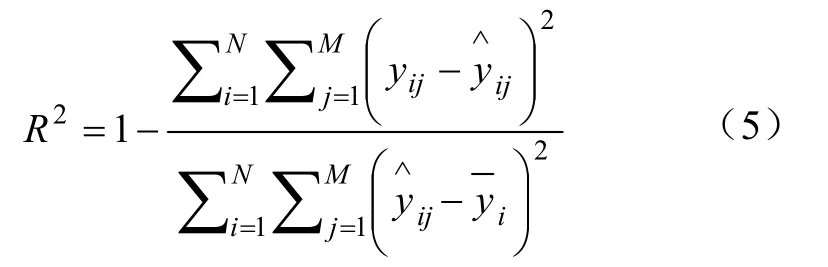
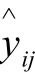
均方根误差(RMSE)主要用来衡量真实值与预测值之间的偏差程度,其计算公式如下所示:
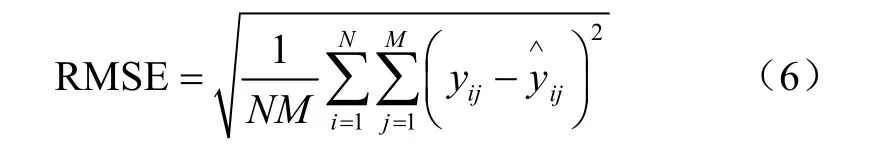
3 结果与分析
3.1 近红外光谱数据采集与预处理
按照本文试验方法采集的原始近红外光谱数据如图 3a所示,可见不同拼配比例的茶样其光谱趋势基本一致。为了消除光谱中诸如高频噪声、基线漂移和散射等因素的影响,本文采用标准正态变换(Standard Normal Variate transform,SNV)方法首先对光谱数据进行预处理,25种拼配茶样的平均光谱如图 3b所示。从图3中可以看出,虽然各种拼配样本的原料茶比例不同,但其光谱曲线极为近似,呈现出高度相关性。从谱线中可以看出,1 482~1 510 nm的吸收峰应为肽键的二次谐波吸收峰,1 898 nm处的吸收峰为肽键的一次谐波吸收峰,这些官能团与茶叶中的氨基酸类物质相关;2 032 nm处的吸收峰反映了O-H的吸收峰;2 100 nm为HC=CH键的吸收峰,可能与茶叶中的多酚类物质相关。
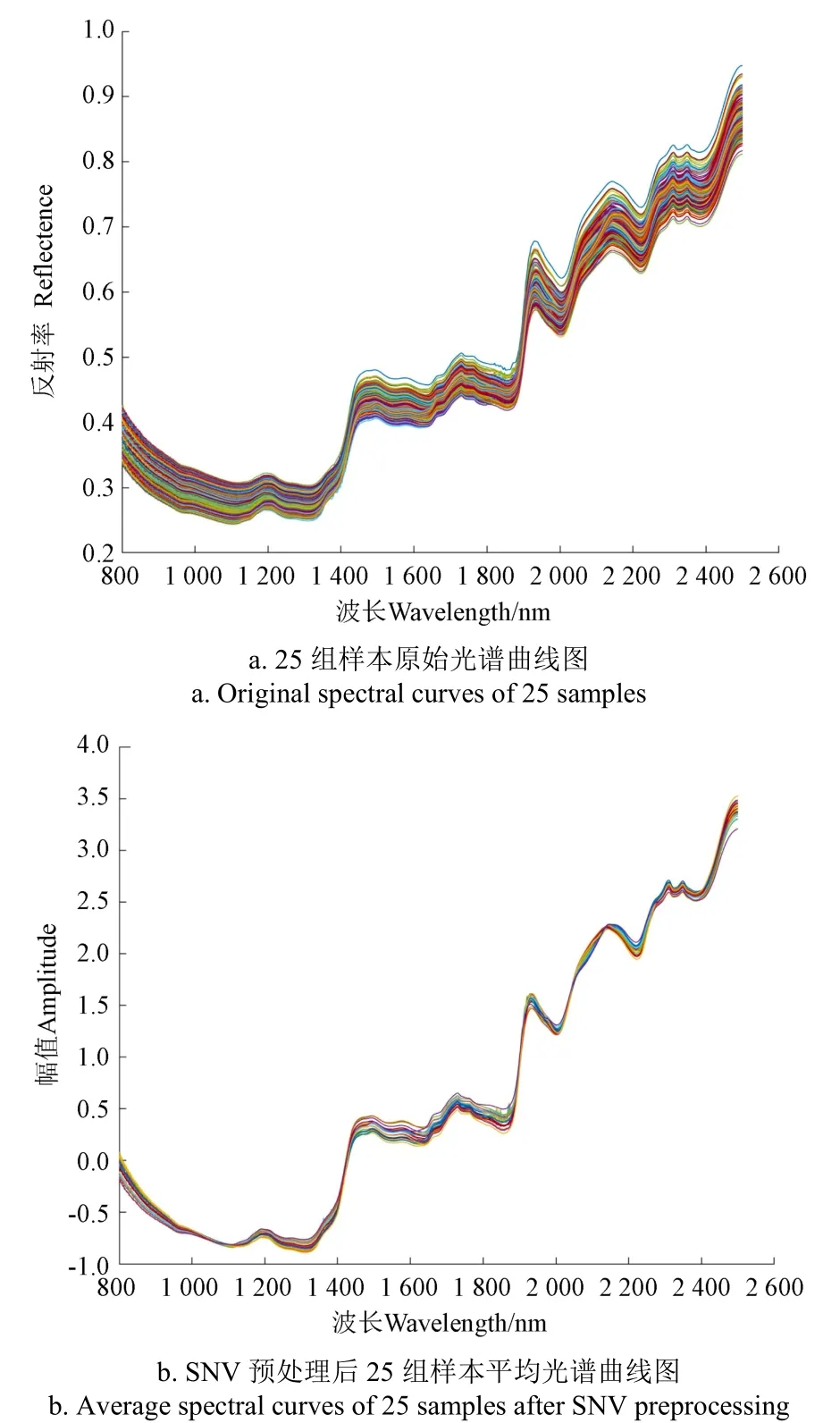
图3 拼配样本的光谱曲线 Fig.3 Spectral curved of blending samples
3.2 基于深度学习模型的拼配比例计算
2.1 不同组别的血清Cys-C、Cr和BUN的水平 随着窒息程度的加重,对照组、轻度窒息组和重度窒息组新生儿的血清Cys-C、Cr和BUN水平均依次增高,见表1。对Cys-C、Cr和BUN分别研究,每一项的重度窒息组、轻度窒息组与对照组两两比较,以Kruskal-Wallis H检验,差异均有统计学意义(P<0.01)。
自动编码器设置为单隐层结构,输入节点数和光谱维度相等为2 203,隐含层的节点个数即为自动编码器提取的特征维数,这一参数和网络性能相关性较强。因此本文以10为步长,在[10,100]维数区间内进行遍历,网络训练完成后,将特征输入Softmax函数,预测拼配比例,结果如图4所示。
采用自动编码器提取特征结合Softmax模型预测方法(AE+Softmax)的拼配比例预测结果如图4所示,图 4a为校准集、验证集和测试集的决定系数随特征维数变化结果,图4b为3个样本集合均方根误差随特征维数变化结果。从验证集结果分析,当特征维数取值为20,决定系数最大为0.916 6,均方根误差最小为7.57%,随着特征维数的上升,决定系数呈现出波动降低的趋势,同时均方根误差也呈现出波动升高的趋势。从图4可以看出,该方法的验证集与测试集决定系数显著低于校准集,而均方根误差显著高于校准集,说明存在一定过拟合现象。
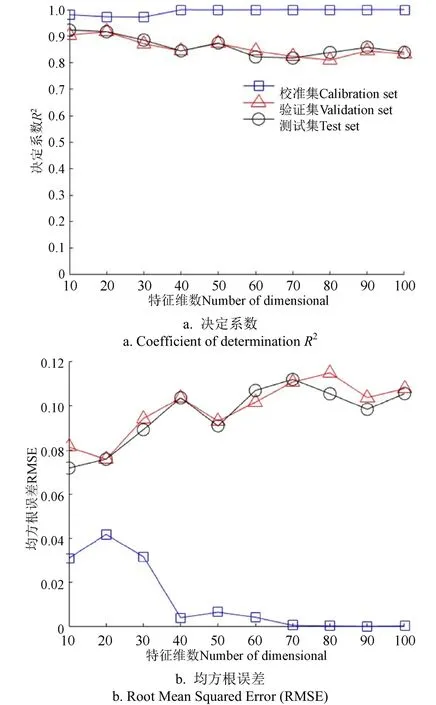
图4 基于自动编码器结合Softmax模型的拼配比例 预测模型性能 Fig.4 Automatic encoder combined with Softmax model to predict the performance of the blending ratio model
卷积神经网络结构复杂,卷积核,网络层数等参数都会影响特征提取结果。本文作者面向祁门红茶的等级评价问题,提出了一种提取近红外光谱数据特征的卷积神经网络,本文在上述研究的基础上设计的卷积神经网络由3个卷积-池化层、1个全连接层和1个用于计算拼配比例的Softmax回归层组成(CNN+Softmax)。由于各样本光谱数值之间的差异较小,所以第一卷积层采用一个较宽的卷积核,便于在较宽的波段捕获光谱特征。然后,1个小的卷积核用于捕获详细的光谱特征。选择整流线性单元(ReLU)作为激活函数,池化层采用最大池化(Max-pooling)。全连接层的每个节点都连接到上一层的特征信息。为了避免过拟合,提高网络的泛化能力,在第3个池化层和全连接层的之间增加了一个Dropout操作,神经元节点失活概率为0.5。最后,连接Softmax回归层。
为了测试不同特征维度对计算结果的影响,同样将维数在[10,100]区间以10为步长做遍历,根据特征维度对网络部分结构参数进行微调。完成网络模型构建后,训练过程可分为3个步骤:1)在所构建网络上加载数据集进行模型参数训练;2)待所构建网络模型收效后,保存训练好的网络权重,以供后续网络微调;3)微调全连接网络,其全连接层学习率为0.05,衰减学习率为0.001,批处理数目为15。计算结果如图5所示。当特征维数从10~100之间变化时,决定系数与均方根误差均呈现了上下波动的趋势,说明单纯增加特征维度并不能提升其精度性能指标。从验证集的性能指标分析,当特征维数取30、40时,性能指标较好,决定系数分别为0.964 0,0.964 3,均方根误差分别为0.049 9,0.047 2。独立测试集的两项性能指标与训练集、验证集差距不大,说明该算法较好反映了数据内部结构特点,对数据的拟合情况较好,详细网络参数如表2所示,此时的网络参数总数为3 305。本文同时对比了采用不同激活函数时计算结果的性能指标,结果如表3所示,在验证集上采用Rule函数的决定系数高于采用Tanh函数和Sigmoid函数的决定系数,而采用Rule函数的RMSE值低于采用Tanh函数和Sigmoid函数的RMSE值,故采用Rule函数的性能指标优于Tanh函数和Sigmoid函数。
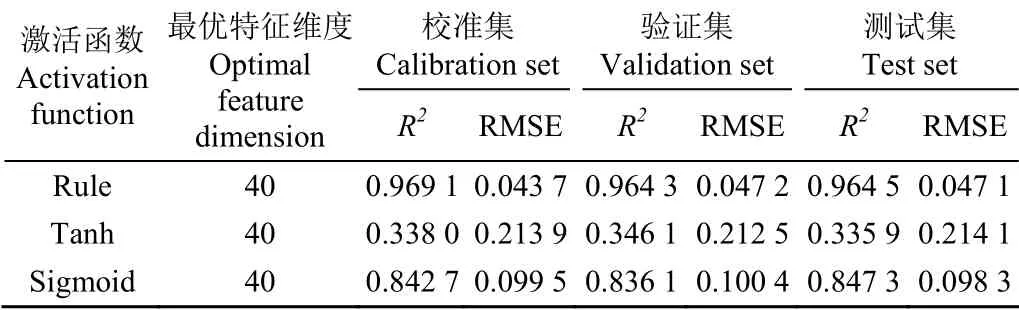
表3 采用不同激活函数时的性能对比 Table 3 Performance comparison under different activation function
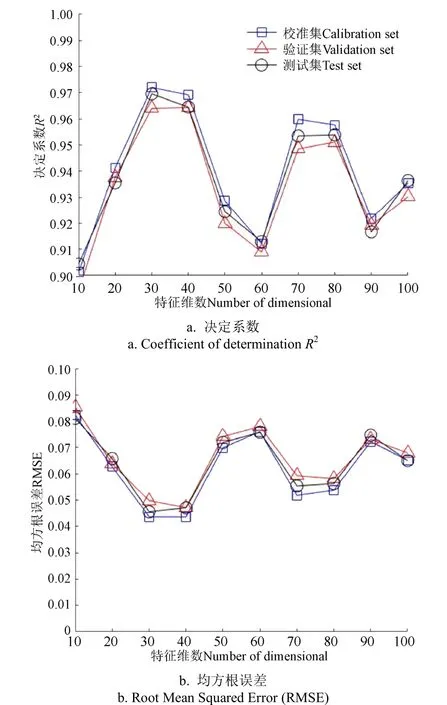
图5 基于卷积神经网络结合Softmax方法的拼配比例 预测模型性能 Fig.5 CNN combined with Softmax method to predict the performance of the blending ratio model
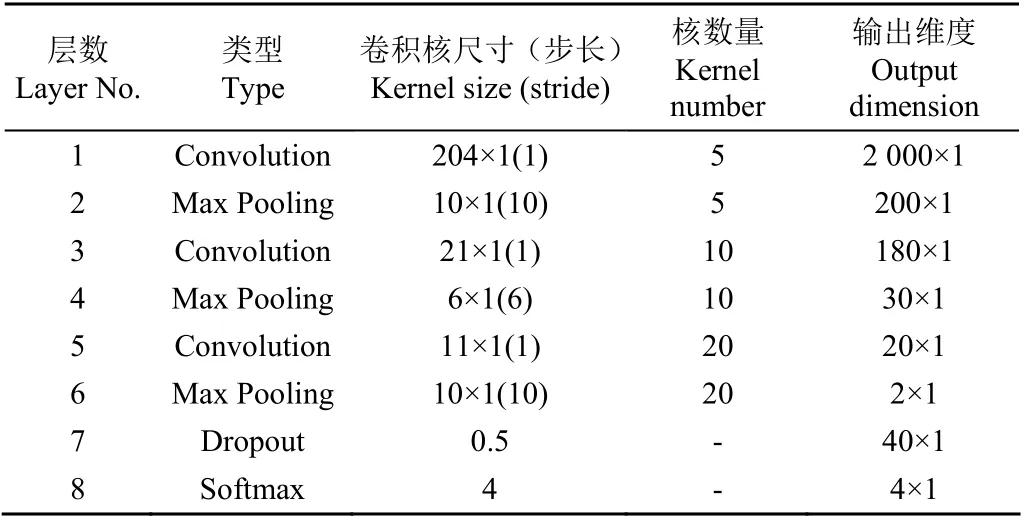
表2 用于预测茶叶拼配比例的卷积神经网络结构参数 Table 2 Structural parameters of the convolutional neural network of tea blending ratio prediction model
本文进一步测试首层卷积核大小对结果影响,第一种网络为首层大卷积核,卷积核尺寸为204×1,后续卷积核依次采用下采样机制;第二种网络为首层小卷积核,首层卷积核尺寸显著减小,后续卷积核依次采用下采样机制,网络结构参数如表4所示,特征维度选择40,80。计算结果如表5所示,可以看出,采用大卷积核的网络结构,其验证集的决定系数和均方根误差均优于小卷积核网络。分析这种现象产生的原因,作者认为,图像识别类机器学习任务存在目标类别多,原始数据差异性较大的特点,而茶样的光谱数据,从趋势上来看基本相似,差异仅存在于部分波段的反射率。此时,若采用小卷积核,将会提取大量相似而又冗余的信息,可能会导致学习效果不佳,甚至网络难以收敛的问题。
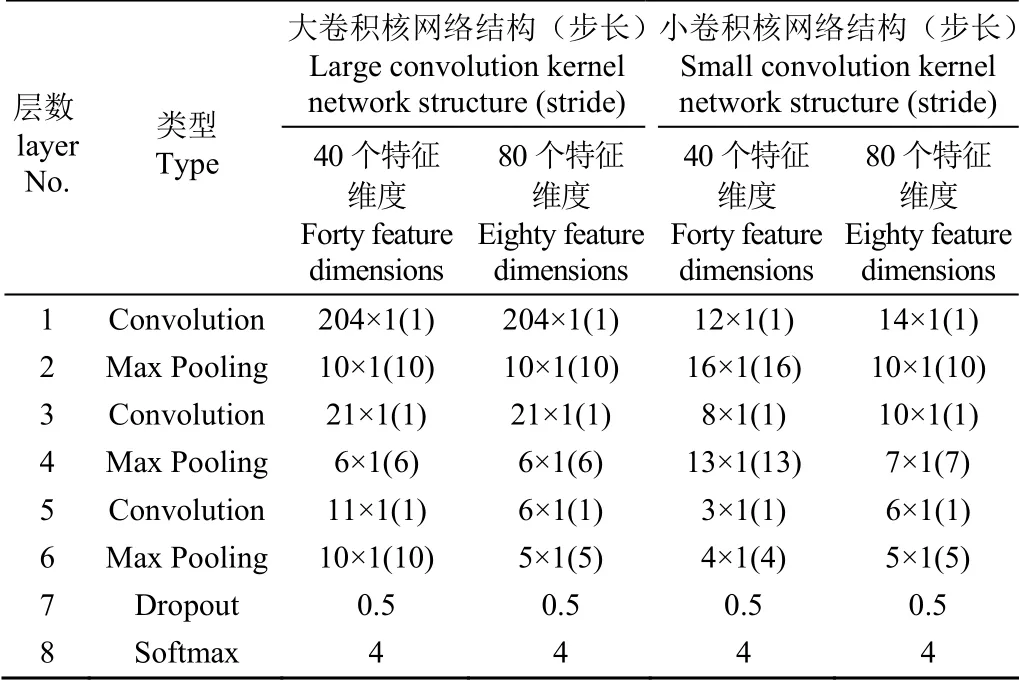
表4 两类不同维度下及不同卷积核大小的网络结构参数 Table 4 Network structure parameters under two different dimensions and different convolution kernel sizes
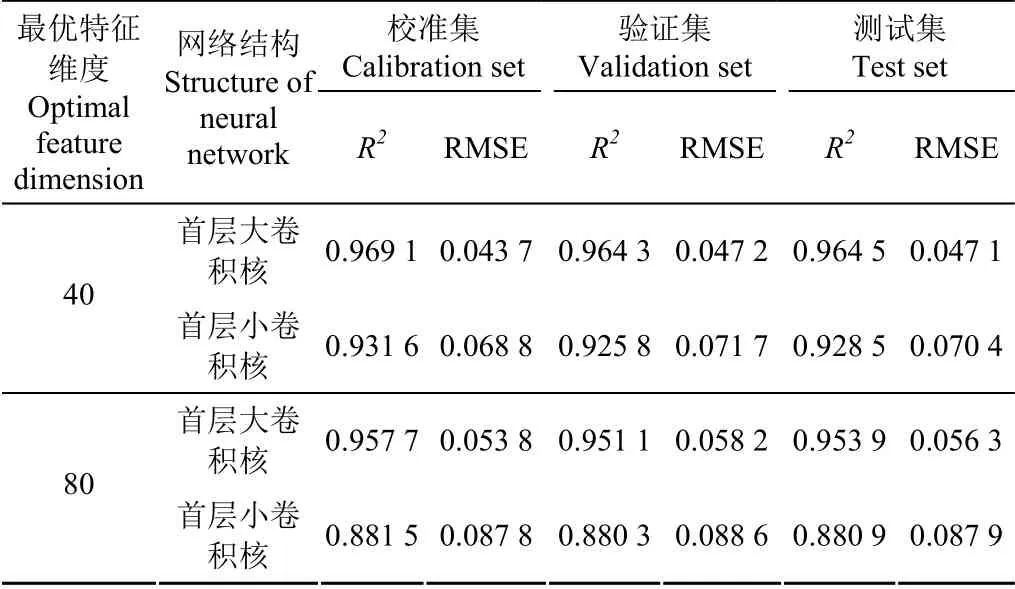
表5 采用不同网络结构时的性能指标对比 Table 5 Performance comparison under different neural network structures
为了对比不同特征提取方法的效果,本文采用经典的PCA方法提取光谱特征,分别采用Softmax与PLS算法,预测各原料茶的拼配比例。为了验证不同维度的特征变量对预测效果的影响,也将降维后维数在[10,100]区间以10为步长做遍历。
在PCA降维后采用Softmax算法(PCA+Softmax)的预测结果如图6所示,在PCA降维后采用PLS算法(PCA+PLS)的预测结果如图7所示,从曲线趋势来看,两种方法有一定共性,即当特征维数在20及以上时,其两项主要性能指标随特征维数变化不大。测试集结果与训练集、验证集并无明显差距,说明没有出现过拟合现象。验证集上定量对比性能指标,可以发现PCA+Softmax的两项性能指标均略高于PCA+PLS方法。
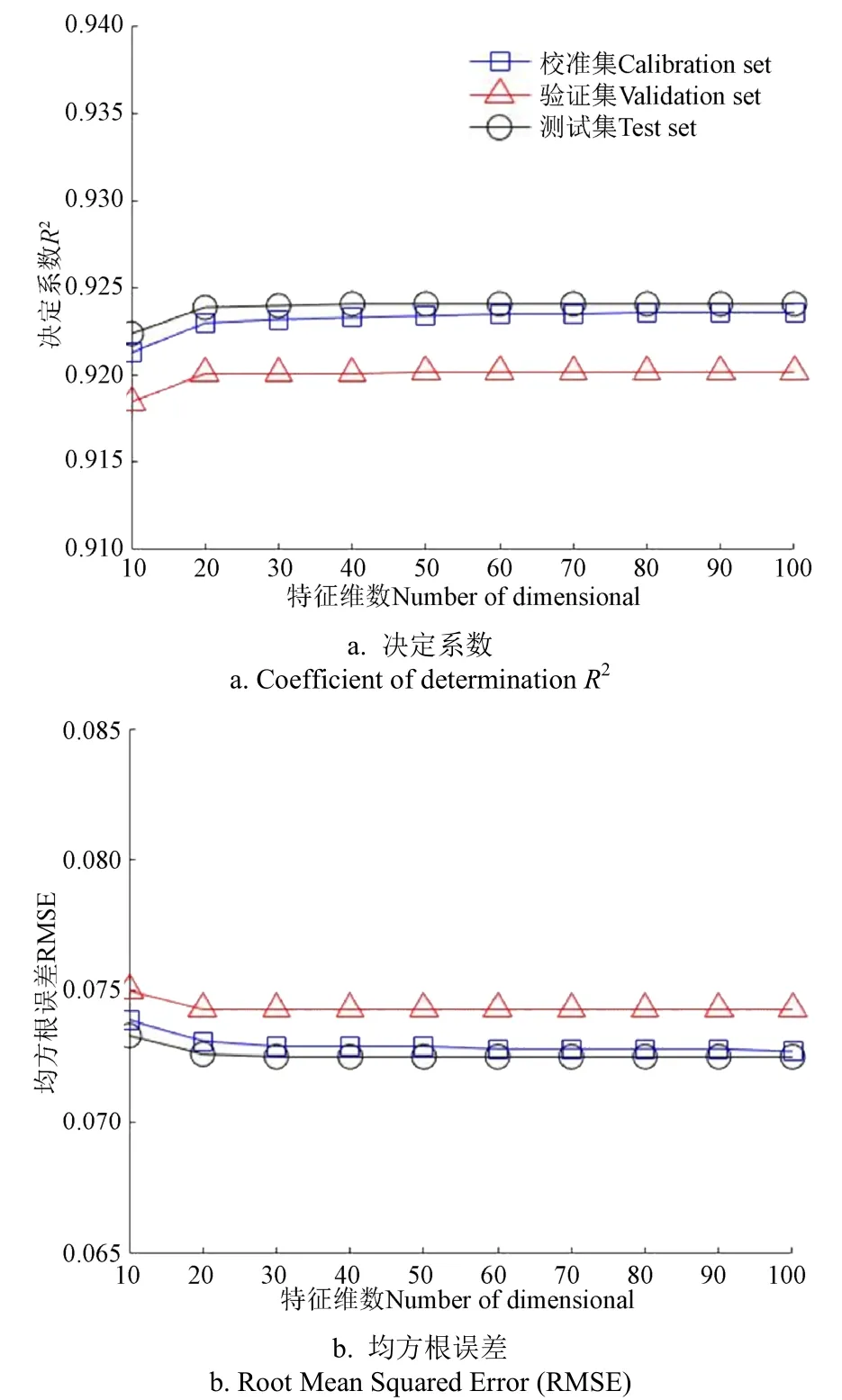
图6 基于PCA结合Softmax方法的拼配比例预测模型性能 Fig.6 PCA combined with Softmax method to predict the performance of the blending ratio model
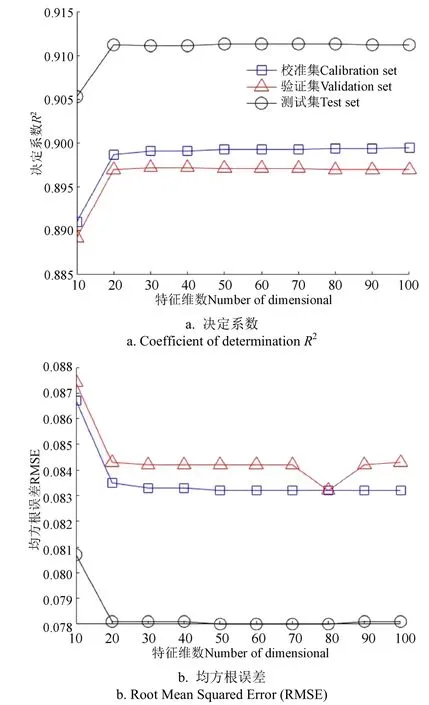
图7 基于PCA结合PLS方法的拼配比例预测模型性能 Fig.7 PCA combined with PLS method to predict the performance of the blending ratio model
3.3 讨 论
验证集性能指标通常作为模型选择的依据,不同方法的验证集决定系数与均方根随特征变量的分布关系如图8所示。对比各类方法的性能指标可以看出,当特征维数在20~100之间变化时,基于CNN+Softmax方法的决定系数普遍高于其他3种方法,其RMSE值普遍低于其他3种方法,说明基于CNN+Softmax的方法更容易获得较好的性能指标。本文采用的3种方法同时采用了Softmax模型预测拼配比例,但基于不同特征提取方法的结果却有显著性差异,说明特征提取方法对预测效果具有显著的影响。同时可以发现,基于PCA特征提取方法的性能在特征维数大于等于20以后基本维持稳定,说明在获得了稳定的特征信息后,算法的性能指标并不与特征数量呈明显相关,尤其是基于PCA的特征提取方法,其特征的方差贡献率往往呈递减趋势,单纯增加特征维数并不能显著提高性能指标。两种深度学习方法也表现出类似的结论,即CNN+Softmax以及AE+Softmax方法的性能和特征维度数量并没有正相关关系。
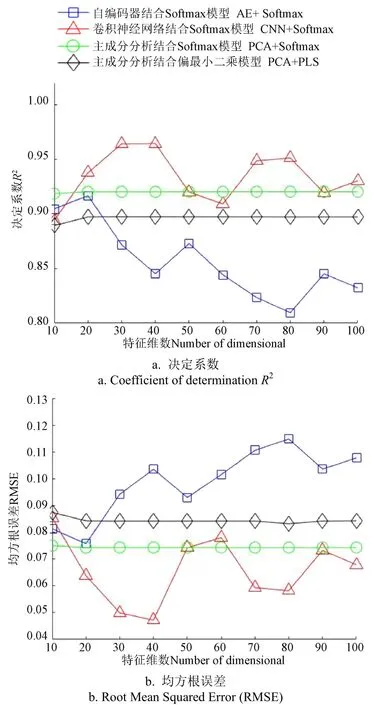
图8 不同方法的性能指标对比 Fig.8 Performance index comparison of different methods
各类方法的验证集最优性能指标与对应的特征维度(同样的性能指标取最小值)如表6所示,从表中可以看出CNN+Softmax方法的决定系数、均方根误差在校准集、验证集、测试集上没有出现较大差异,说明算法具有较好的泛化能力,均方根误差值均在5%以下,误差指标较为理想。
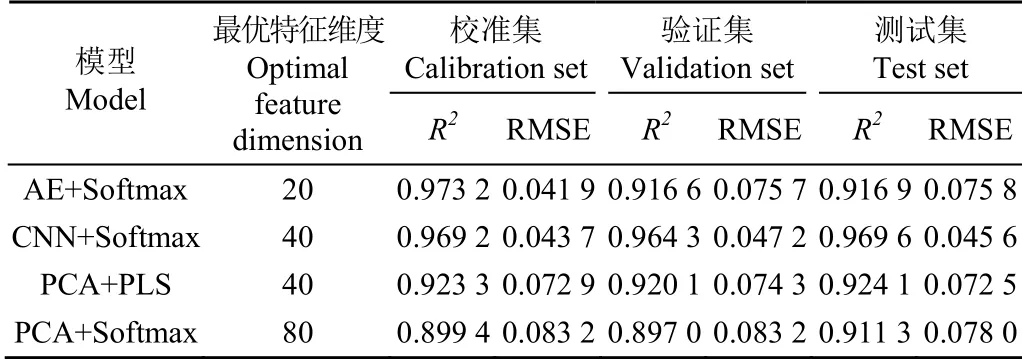
表6 各类方法最优预测精度对比 Table 6 Optimal prediction accuracy comparison of various methods
滋味品质调控是茶叶拼配过程中的必要内容,特别是对于大宗出口的炒青绿茶,相对外形指标,客户往往更加关注滋味。滋味品质的形成往往和茶叶中的主要化学成分相关,近年来的研究成果证明,近红外光谱数据可以有效表征茶叶中茶多酚、儿茶素等主要化学成分,而滋味品质的调控是调节通过不同原料茶的比例来达成,这也是本文尝试采用近红外光谱数据预测拼配比例的机理。
从试验数据中可以看出,尽管不同样品之间的拼配比例不同,但是其近红外光谱数据的趋势一致,幅值差异性很小,表现出高度的相关性。传统的多元线性回归方法往往难以解决这一问题,通过本文的研究结果可以发现,特征提取方法是提高预测模型性能指标的关键。卷积神经网络由于其高效的特征提取机制,更容易从近似的光谱信号中提取差异性特征信息,以较高精度实现拼配比例预测。
本文采用2种深度学习的方法提取光谱数据特征,一般认为深度学习方法需要大量的样本数据,而本文的样本数据仅为500个,小样本训练模型的可靠性和泛化能力是机器学习领域关注的共性问题。本文中,基于自动编码器的模型就出现了过拟合现象,数据量不足可能就是导致该问题的原因之一。本文的研究目的和基于图像的目标识别问题是不同的,ImageNet数据集包含了数万个类别的样本,本文仅为4种茶样按照不同比例拼合后的25种,样本类别不在一个数量级上。从茶样的数据特点来看,其光谱数据虽然维度较大(2 203×1),但是不同类别样本的数据趋势高度类似,差异仅存在于部分波段的反射率。深度网络的任务是从相似的光谱数据中,提取差异性信息。结合以往的研究结果和同类文献报道来看,样本数量在数百个有望达到较好的效果。为了验证本文提出模型的泛化能力,作者也进行了多折交叉验证,性能指标显示模型也具有较好的性能。后续作者将进一步收集不同年份、批次、产地的产品,积累相关数据,对预测模型的预测能力和泛化能力做出更为深入的研究。
4 结 论
本文以眉茶为研究对象,针对其拼配比例构建问题,提出了一种基于近红外光谱数据的拼配比例计算方法,并模拟茶叶拼配过程,构造了多组不同含量的茶样,通过预测方法的计算结果与预设比例的误差统计值评价预测方法的性能。本文采用的4种方法,包括AE+Softmax(自编码器结合Softmax模型)、CNN+Softmax(卷积神经网络结合Softmax模型)、PCA+Softmax(主成分分析结合Softmax模型)及PCA+PLS(主成分分析结合偏最小二乘模型模型),其中基于卷积神经网络结合Softmax模型的方法性能较好,当特征维度为40时,其验证集决定系数为0.964 3,均方根误差为0.047 2,优于其他方法,经过测试集测试后的性能指标与验证集较为接近,说明算法具有较好的泛化能力。尽管构造茶样中各原料茶的含量不同,但是各类茶样的近红外光谱数据相似性较强,所以常见的回归计算方法精度不高,卷积神经网络由于其高效的特征提取机制,获得了较为理想的效果。
茶叶拼配问题,需要调控的质量因子较多,除了滋味品质外,外形也是十分重要的质量因子,这是近红外光谱数据无法表征的,也是我们后续需要进一步开展的工作。

