高速铁路车站作业计划可靠性链式优化研究

徐通

（中国铁路经济规划研究院有限公司 研究实习员，北京 100038）

0 引言

高速铁路车站既是服务旅客的窗口，也是运输组织的核心节点，作业计划的优劣将影响局部甚至整个路网的运输质量，所以对作业计划的安全性和可靠性要求较高。高速铁路车站作业计划优化问题也一直是国内外众多学者热衷于研究的经典问题，众多的国内外学者从各种角度出发对车站作业计划的各方面指标进行优化，文献[1]以稳定性强和接发车进路条件最优为目标，对车站作业计划进行优化，文献[2]以提高鲁棒性和到发线资源占用的均衡性为目标对车站作业计划进行整体优化，文献[3]以提高车站作业计划对列车运行波动适应能力为目标，提出了一种车站作业计划二次优化的局部搜索算法。文献[4]研究建立了给定运行图条件下的车站到发线运用计划编制模型，并提出了对到发线利用进行优化的遗传算法，文献[5]从抗干扰能力方面对车站作业计划进行优化。

本文根据我国高速铁路车站实际运输组织方法，从可靠性入手，创立综合干涉系数概念，结合时-空作业链模型，为车站作业计划可靠性优化提供了一个新的优化思路。能对高速铁路车站作业计划可靠性的提高提供重要依据，也对提高我国旅客运输服务质量与保障落实高速铁路按图行车具有重要意义。

1 问题描述

车站作业计划是一个包含时间、空间两个维度的作业计划，规定了列车在各个作业过程对车站设备的占用与释放时间。列车在车站中对道岔区段等设备，按一定顺序占用并且释放过程的链式描述称为列车的时-空作业链[6]。

一个可行的车站作业计划需要在运行图中约束的列车接、发车时刻下，合理安排进路，保证每个车站作业进路的时间维度与空间维度上不存在冲突。一个可靠性高的车站作业计划应该能在某一列车发生晚点时，一定程度上减轻初始晚点对后续列车的影响，阻止晚点进一步传播。

在列车到、发时刻固定的情况下，可以通过优化作业链的空间占用，降低列车间的相互影响关系，提升车站作业计划的可靠性。本文借鉴文献[7]将两列车冲突冗余的倒数称为“冲突系数”的做法，将两条作业链所有区段“冲突系数”的和定义为这两条作业链的“综合干涉系数”，代表两列车在道岔区段层面相互干涉关系的大小。以所有作业链间总综合干涉系数最小为可靠性优化目标，以车站连锁条件为约束，建立基于列车时-空资源占用函数的优化模型。

2 问题分析与建模

2.1 作业链时-空资源占用函数

在列车时-空作业链模型中，时间层面，列车走行过程中对各车站资源进行占用与释放；空间层面，列车依次占用进路中各道岔区段、股道等资源。根据“一次办理，分段解锁”规则，办理进路完成后，进路中的所有设备同时开始占用，道岔区段与股道的状态变为占用。假设一列列车a按车站作业计划占用作业链i，i包含多条进路，其中的r进路包含n个道岔区段S1,S2,S3,S4…Sn。假设进路r的开始时间为，然后按照“一次办理、分段解锁”的原则，其包含的S1,S2,S3,S4…Sn等道岔的占用与开始时间全部相同，即

但是由于采用“分段解锁”的方式，对于某一道岔区段，在被列车的轮对经过之后，其本身的设备状态由占用状态转换为空闲状态。假设某道岔区段s在其进路r距离起点j个道岔区段，那么其占用时间为进路开始时间，其解锁时间为进路开始时间加上列车经过j个道岔区段与列车长度距离的走行时间。其走行距离为l解，s：

式中：l列为列车的长度；lr,c为进路r中第c个道岔区段的长度。

接发车作业中列车的走行方式可抽象为三个部分，分别为匀加速直线运动部分（列车启动过程）、匀速运动部分（列车匀速运行过程）和匀减速直线运动部分（列车制动过程）。所以，在已知列车到道岔的走行距离与加速或减速加速度之后，可求得道岔区段s的锁闭时长为：

所以道岔区段s的起止时刻可由下式表示：

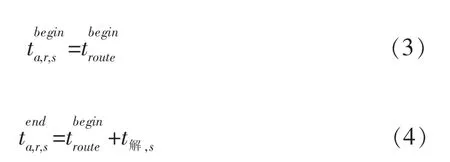
道岔区段或股道s的时间占用函数为0-1变量，其函数表达式为：

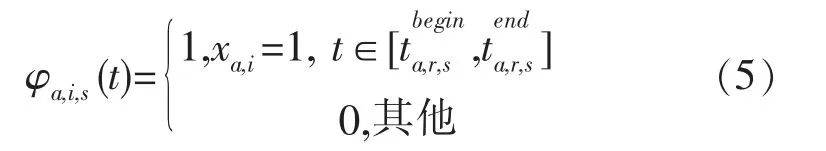
2.2 作业链综合干涉系数计算

由前文定义可知，计算综合干涉系数的前提是计算两列车共同占用道岔区段的冲突系数和。本文基于“分段解锁”的现场实际，通过作业链描述列车对时-空资源的占用过程，以道岔区段和股道为最小研究单位，更为精确地界定两列车的冲突系数。

若列车a的作业链为i，列车b的作业链为j，且两车先后共同占用的道岔区段（或股道）S1、S2…Sn，则此时列车a、b在道岔区段Si上的冲突系数为：

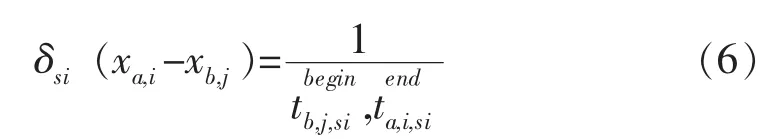
下面通过图1进一步介绍综合干扰系数：

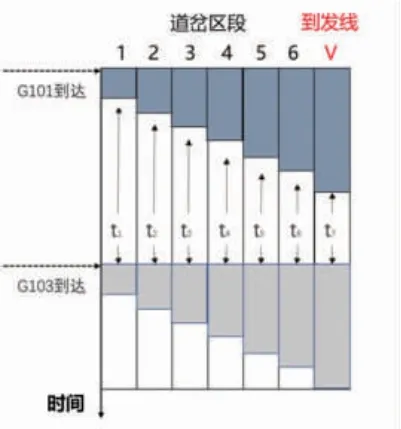
图1 列车间的综合干涉系数

在图1中，列车G101与G103相继到达，两列车共同占用道岔1、道岔2…道岔6与到发线V，缓冲时间分别为t1、t2…t7，所以两列车的综合干涉系数为1/t1+1/t2+1/t3+1/t4+1/t5+1/t6+1/t7。

假设S为车站内所有道岔区段的集合，s为某一道岔区段，L为车站内所有到发线的集合，l为某一到发线，为两列列车在道岔s的缓冲时间，为两列列车在到发线l的缓冲时间。

所以，任意两列相邻列车Xi与Xi+1的综合干扰系数φ（Xi,Xi+1）为

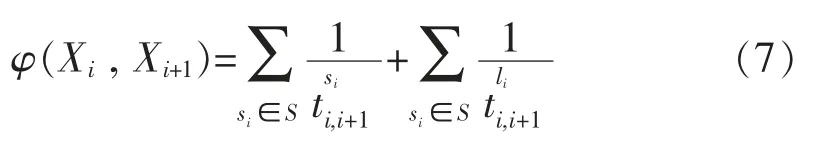
2.3 模型

考虑到实际求解规模和求解难度，在不考虑转线折返列车的假设下，以车站作业计划的综合干涉系数之和最小为优化目标，以时-空作业链对车站作业计划中各列车对车站资源的占用情况进行描述。在车站平面图、列车运行图（列车时刻表）、列车技术作业时间标准与动车组运用计划已知的情况下，建立模型如下：

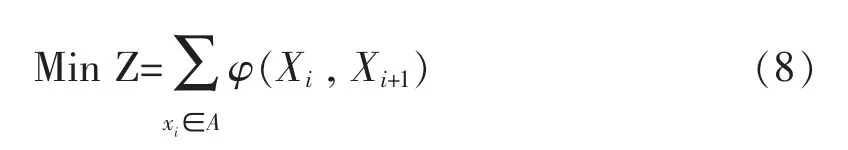
列车作业链安排约束：

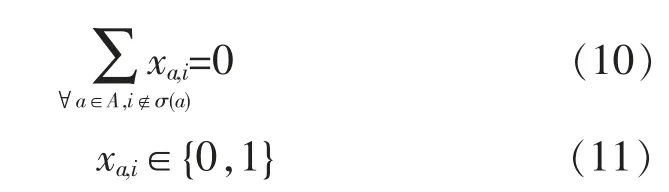
股道占用冲突约束：

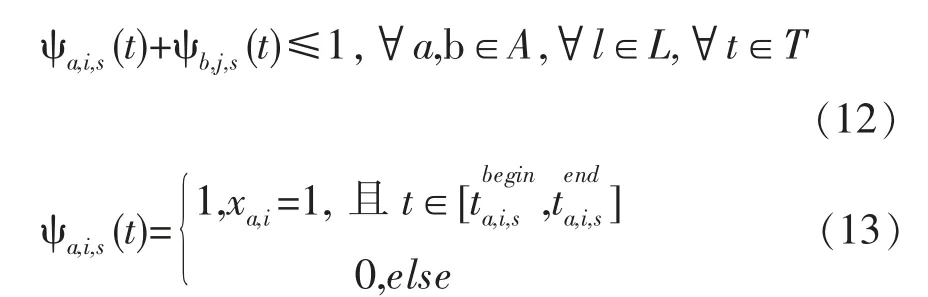
道岔区段占用冲突约束：

模型中各符号含义如表1所示：

表1 模型符号说明

式（8）为模型优化目标，表示车站作业计划的综合干涉系数之和最小。式（9）表示对于每一列列车而言，只能在其可选作业链集合中至少且只能选择一条时-空作业链；式（10）对式（9）进行补充，表示列车作业链的选择范围，即不可以在不可选作业链集合中选择时-空作业链；式（11）表示作业链的取值约束，代表作业链被选取时取值为1，否则取值为0。式（12）与式（13）表示股道在同一时间只能被一条作业链占用，式（14）与式（15）表示道岔区段在同一时刻只能被一条作业链占用。

3 案例分析

以北京南站高速场为例，其车站平面图见图2。车站包含12条到发线，右侧衔接四个方向，其中正线衔接京沪高速铁路的上下行。另外的两条线是动车走行线，与北京动车段相连，北京南站高速场而且两条动车走行线都可以进行车底的出入段作业，北京南站高速场的车底在进行出入段作业时可选择任意一条线。

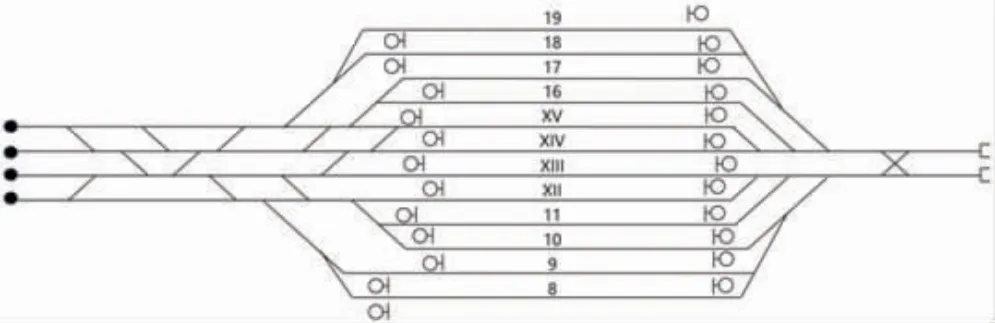
图2 北京南站高速场平面图

北京南站高速场车站时刻表包含高速动车组列车250车次，125对；列检车6车次，3对；动车组2车次，1对；总计258车次，129对。在初始车站作业计划中，共包含本线折返列车184车次，92对；出段始发列车与入段始发列车各37车次。

北京南站高速场的作业主要为始发、终到与本线折返列车。各类列车的技术作业时间如下：终到入段列车最小停站时间20 min、出段始发列车最小停站时间30 min，接发车启动、减速加速度±1.1 m/s2，提前进路办理时间3 min。

依据本文构建的模型，利用遗传算法进行求解。根据北京南站高速场的实际车站作业计划为初始方案，在此基础上迭代调整列车作业链，经算法优化，得到优化后的车站技术作业计划，优化后方案在全计划周期内共调整103列列车。为对比作业计划优化前后的调整内容，取较为繁忙的18:00-20:00时段，对比结果如表2与表3所示。

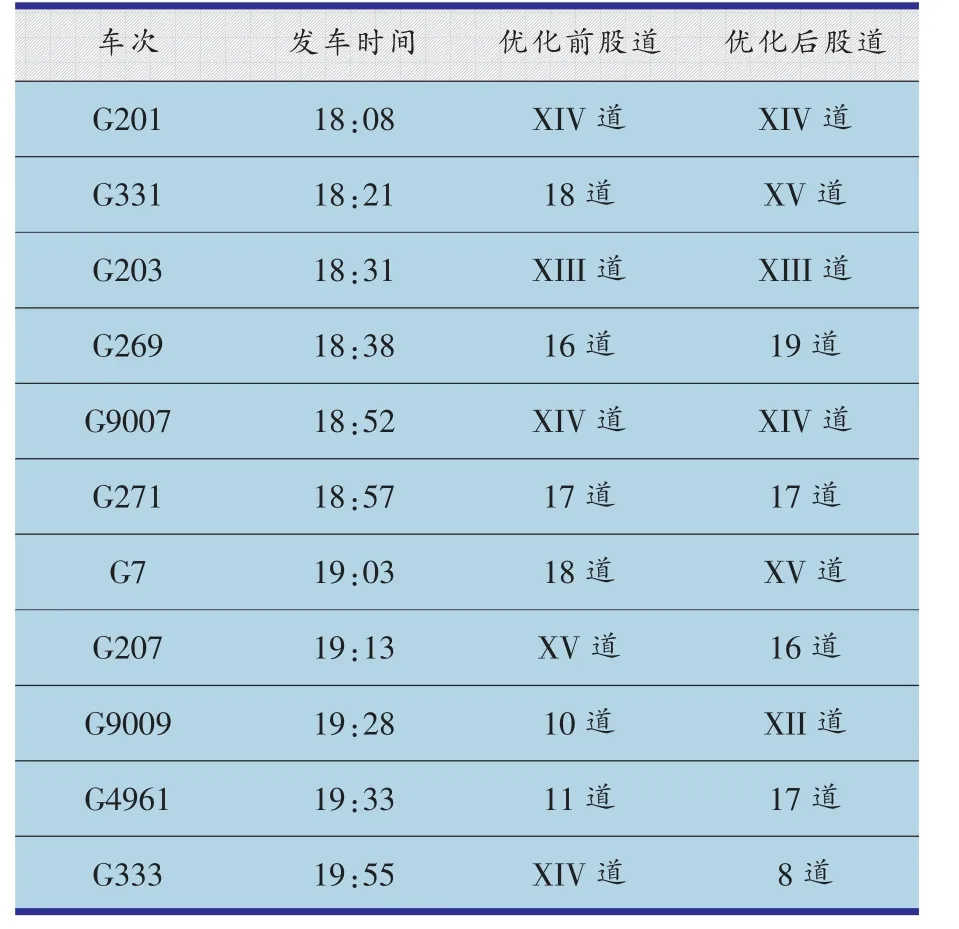
表2 始发列车优化前后股道占用表

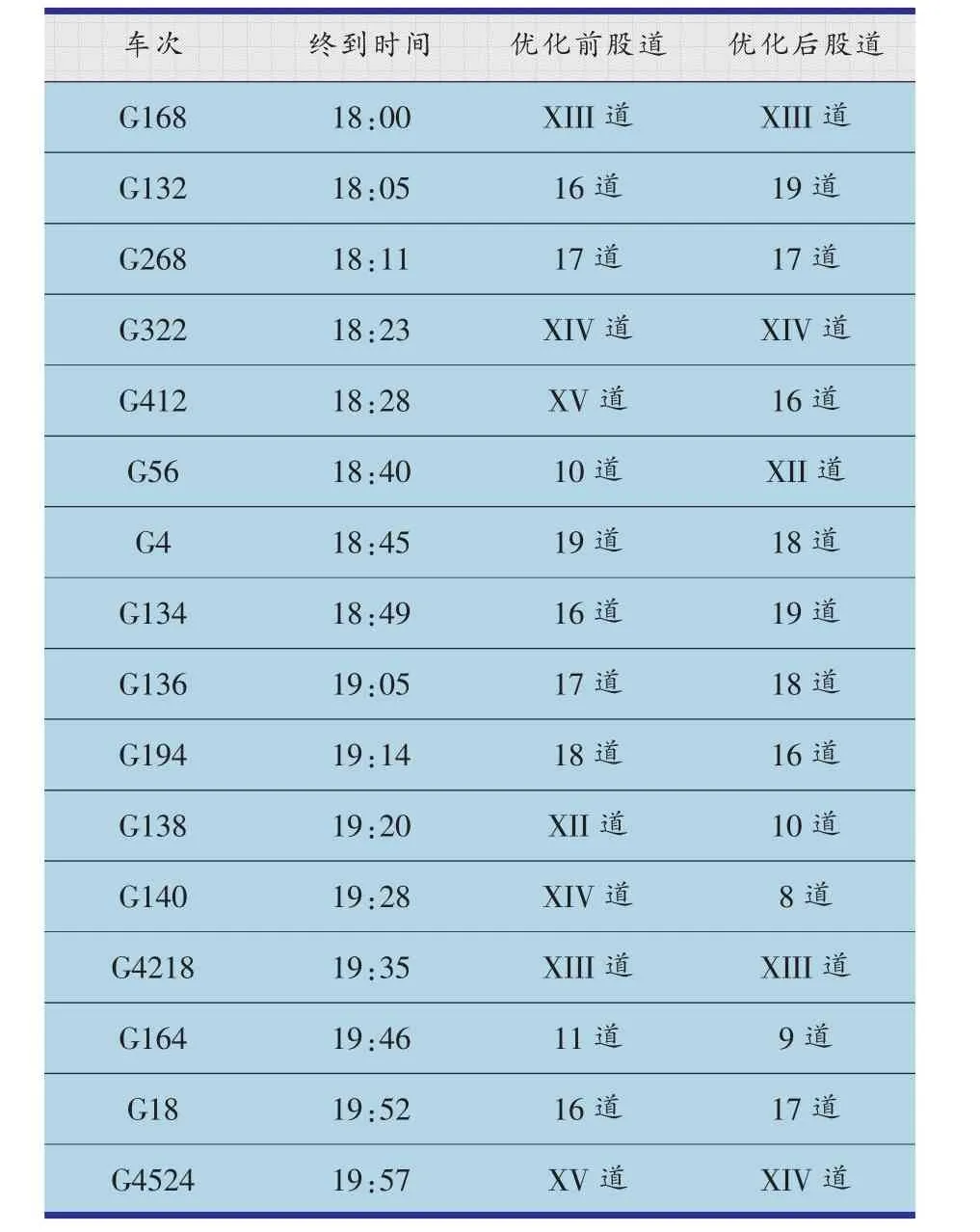
表3 终到列车优化前后股道占用表

由上表可知，在18:00-20:00时间段内，共有始发列车11列，终到列车16列。经过优化之后有7列始发列车与13列终到列车的到发线运用得到调整，未对其接发车时间进行调整。例如始发列车G331由18道调整到XV道；终到列车G132、G134由16道调整到19道。

经过算法迭代，不断优化列车作业链，数据显示，综合干涉系数由486.6降至413.5，下降15%，算法求解的迭代效果见图3中的所示。所以，本文的模型能有效降低高速铁路车站作业计划的综合干涉系数，有效提升车站作业计划的可靠性。

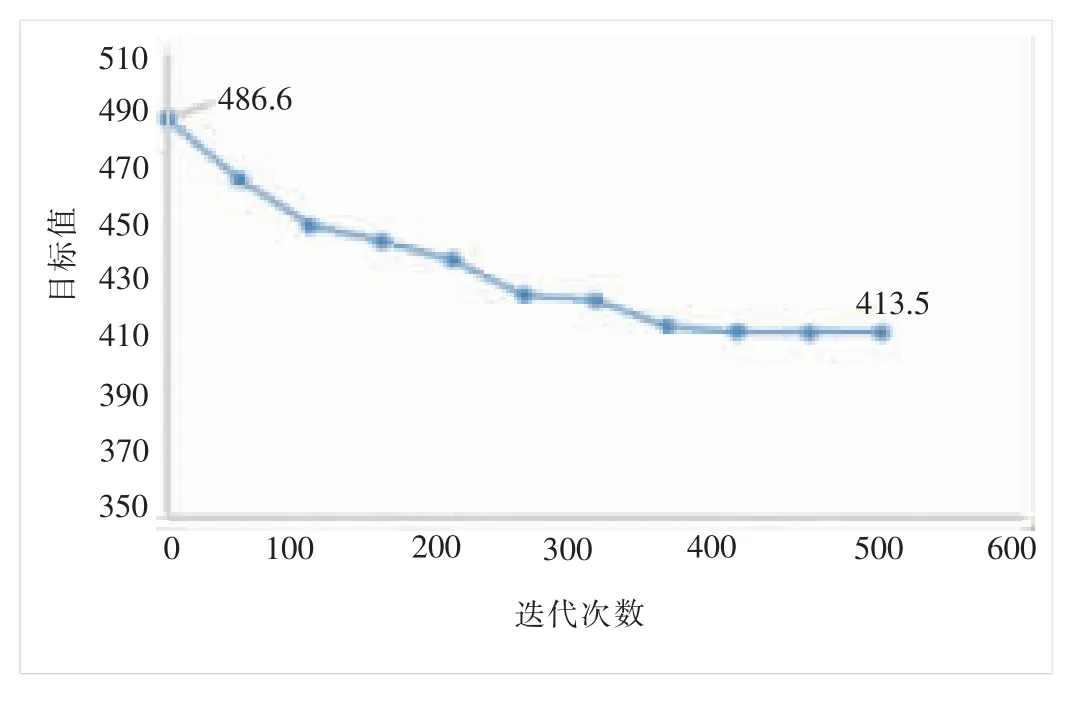
图3 算法求解的迭代图

4 结束语

本文用时-空作业链对列车作业进行描述，以道岔区段和股道为最小单位计算作业链的时-空占用函数，精度较高。然后创立综合干涉系数概念，并以之最小为目标函数对高速铁路车站作业可靠性进行建模与求解。在不改变列车接发车时刻的情况下，通过优化作业链的空间资源序列，进而降低列车间的相互影响关系，提高车站作业计划的可靠性。

在研究范围上，本文模型主要考虑列车方面的扰动对车站资源的影响，没有将车站资源本身的故障因素（例如道岔故障、到发线故障等）考虑在内。在进一步的研究中，将拓展研究范围，将车站资源等故障产生的干扰纳入进来，研究车站作业计划的可靠性。